Entraîner des modèles à base d’énergie à variable latente

🎙️ Alfredo Canziani

Énergie libre

L’énergie libre correspond à :

\[F_\infty (\vect{y})=\min_z E(\vect{y},z) = E(\vect{y},\check z)\]

Ici, $F_\infty$ est la limite vers zéro de la température de l’énergie libre et $\vect{y}$ est un vecteur 2D. Cette énergie libre est la distance euclidienne quadratique par rapport à la variété du modèle. Tous les points qui se trouvent dans la variété du modèle ont une énergie nulle. En s’éloignant, elle augmente de façon quadratique.

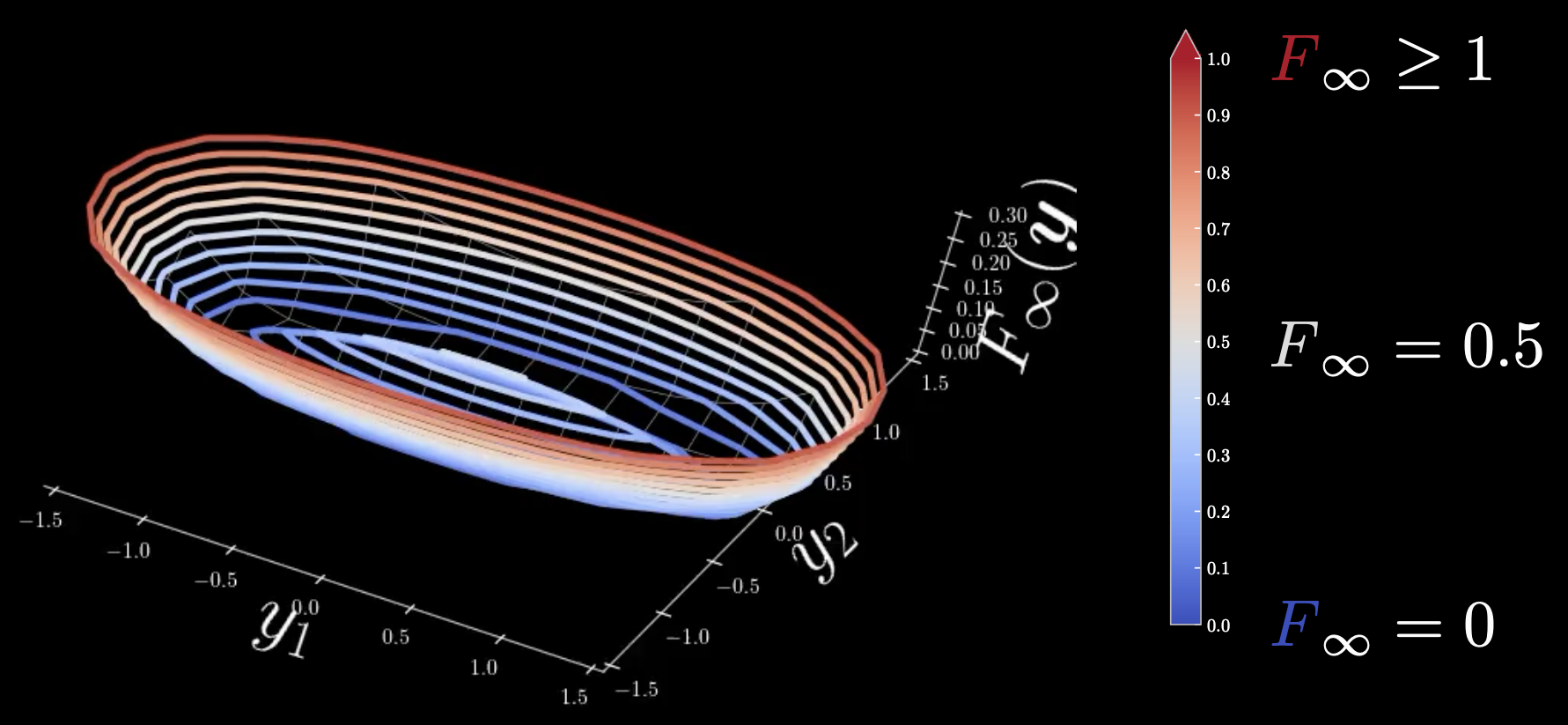
Figure 1 : Carte thermique chaud-froid

Froid : $F_\infty = 0$, chaud : $F_\infty = 0,5$, brûlant : $F_\infty \geq 1$

Toutes les régions autour de l’ellipse qui se trouve avec la variété en ellipse ont une énergie nulle. Au centre, il y a une limite vers zéro de la température de l’énergie libre qui est infinie. Pour éviter cela, nous devons détendre l’énergie libre à une énergie sans minima locaux afin qu’elle devienne plus lisse.

Regardons de plus près $y_1=0$, avec la carte thermique suivante :

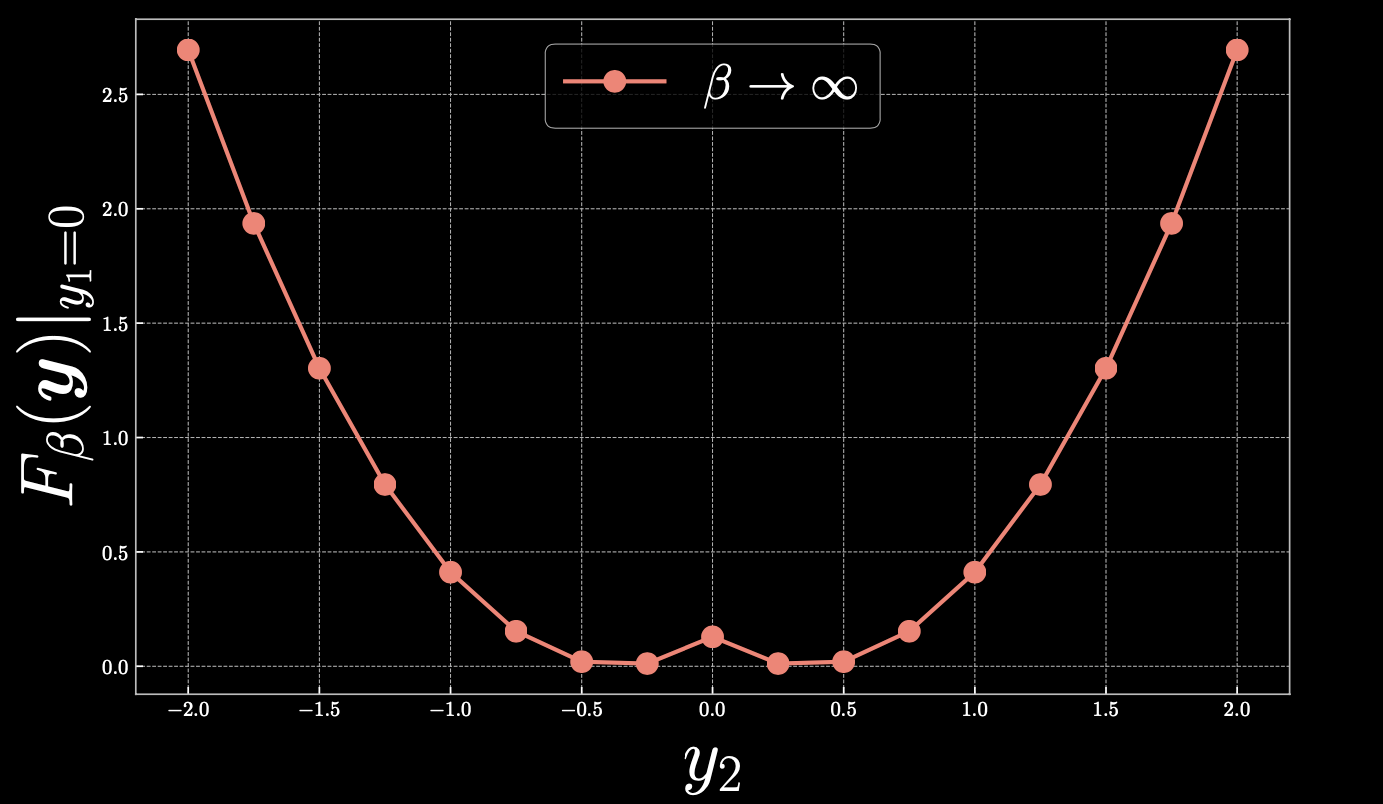
Figure 2 : Coupe longitudinale de la figure 1

Si nous prenons $y_2=0,4$, $F_\beta(\vect{y})=0$ et lorsque nous nous éloignons linéairement du point vers la droite, l’énergie libre augmente de façon quadratique. De même, si nous nous déplaçons vers 0, nous finissons par monter vers la parabole, créant un pic au centre.

Version détendue de l’énergie libre

Afin de lisser le pic que nous avons précédemment observé, nous devons détendre la fonction d’énergie libre de telle sorte que :

\[F_\beta(\vect{y})\dot{=}-\frac{1}{\beta} \log \frac{1}{\vert\mathcal{Z}\vert}{\int}_\mathcal{Z} \exp[{-\beta}E(\vect{y},z)]\mathrm{d}z\]

où $\beta=(k_B T)^{-1}$ est la température inverse, constituée de la constante de Boltzmann multipliée par la température.
Si la température est très élevée, $\beta$ sera extrêmement faible et si la température est froide, alors $\beta\rightarrow \infty$.

Approximation discrète simple :

\[\tilde{F}_\beta(\vect{y})=-\frac{1}{\beta} \log \frac{1}{\vert\mathcal{Z}\vert}\underset{z\in\mathcal{Z}}{\sum} \exp[{-\beta}E(y,z)]\Delta z\]

Ici, nous définissons $-\frac{1}{\beta} \log \frac{1}{\vert\mathcal{Z}\vert}\underset{z\in\mathcal{Z}}{\sum} \exp[{-\beta}E(\vect{y},z)]$ pour être le $\smash{\underset{z}{\text{softmin}}}_\beta[E(\vect{y},z)]$, de sorte que la relaxation de la limite vers zéro de la température de l’énergie libre devient le softmin réel.

Exemples :

Nous revenons sur les exemples de la partie précédente et regardons les effets de l’application de la version détendue.

Cas 1 : $\vect{y}’=Y[23]$

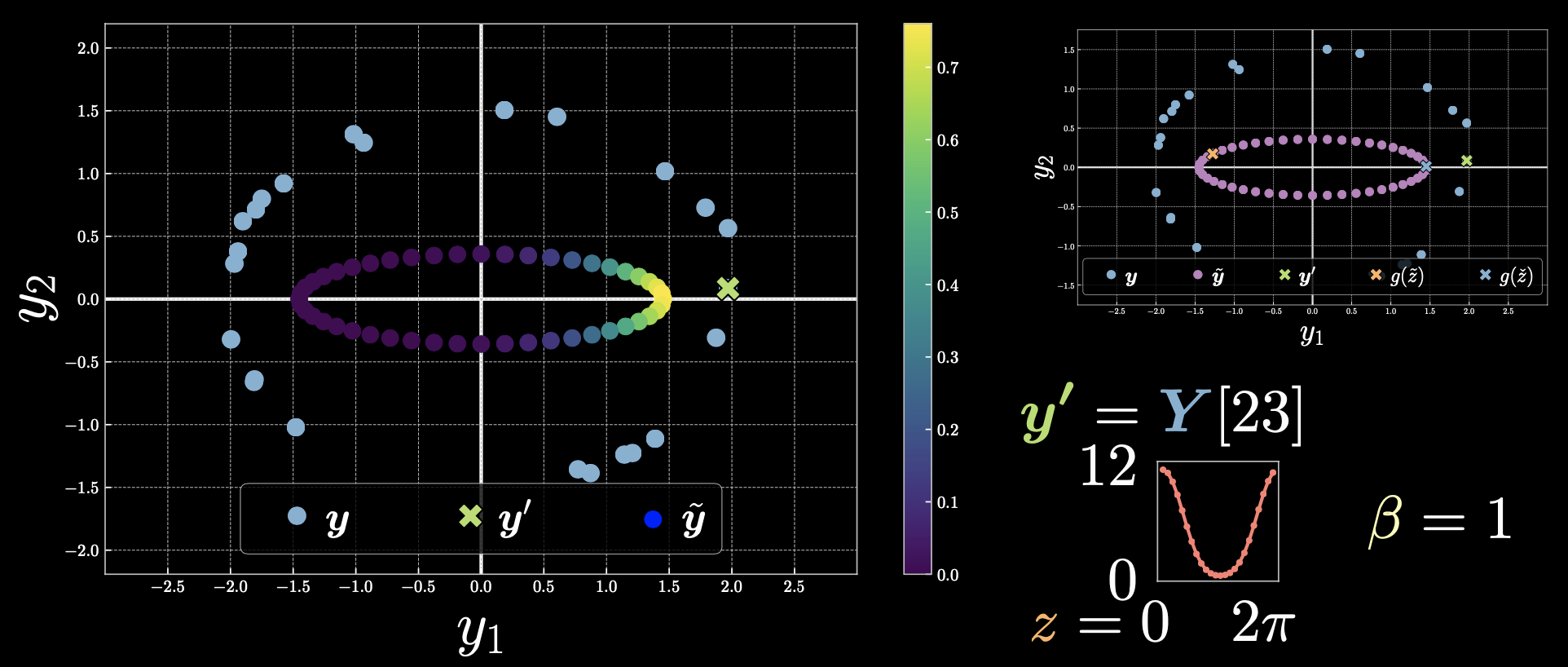
Figure 3 : Cas 1

Les points qui sont plus proches du point $\vect{y}’$ ont une énergie plus faible et donc l’exponentielle est plus grande. Pour ceux qui sont plus éloignés l’exponentielle est nulle.

Cas 2 : $\vect{y}’=Y[10]$

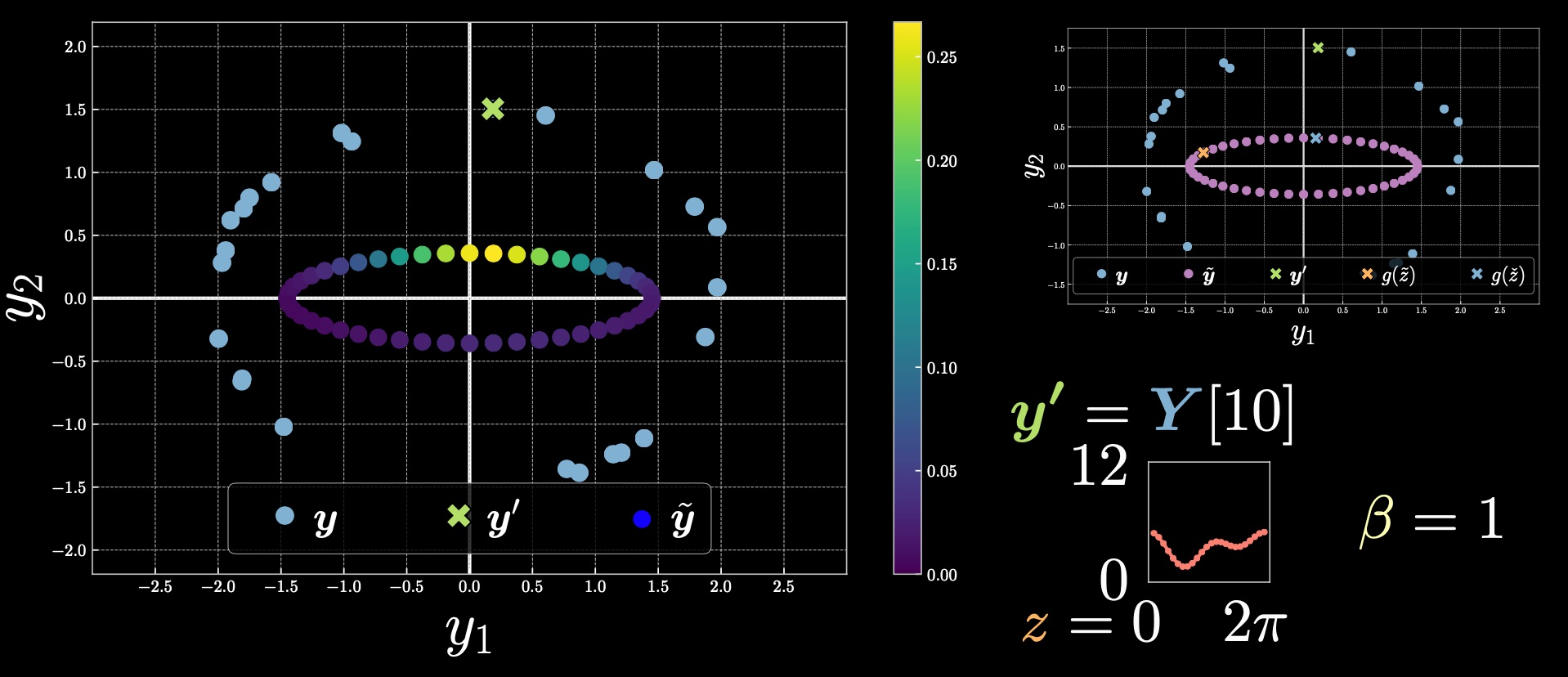
Figure 4 : Cas 2

Nous remarquons que la gamme des barres de couleur a changé par rapport à l’exemple précédent. La valeur supérieure ici est dérivée de $\exp[-\beta E(\vect{y},z)]$.

Cas 3: $\vect{y}’=(0,0)$.

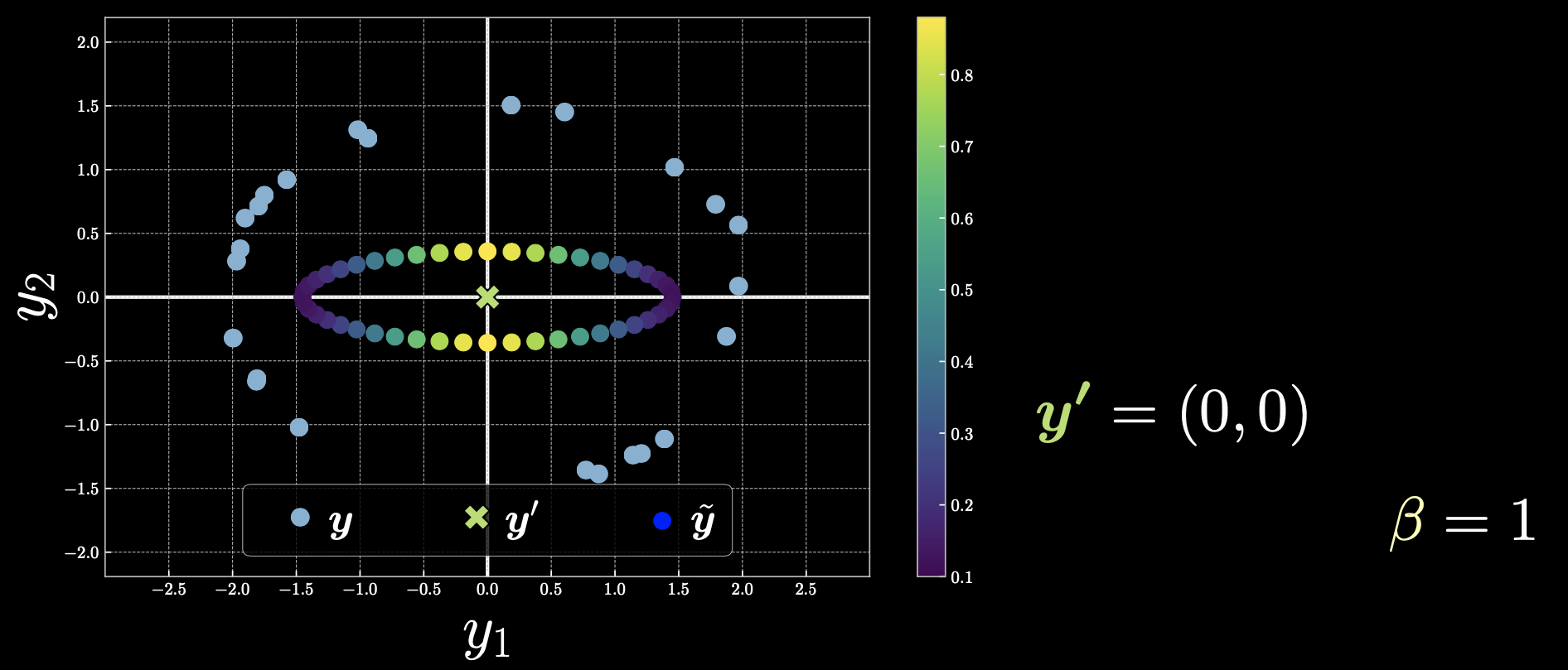
Figure 5 : Cas 3

Si nous choisissons $\vect{y}’$ comme origine, alors tous les points contribuent et l’énergie libre change de façon symétrique.

Maintenant, revenons à la façon dont nous pouvons lisser le pic qui s’est formé en raison de l’énergie froide. Si nous choisissons l’énergie libre plus chaude, nous obtenons la représentation suivante :

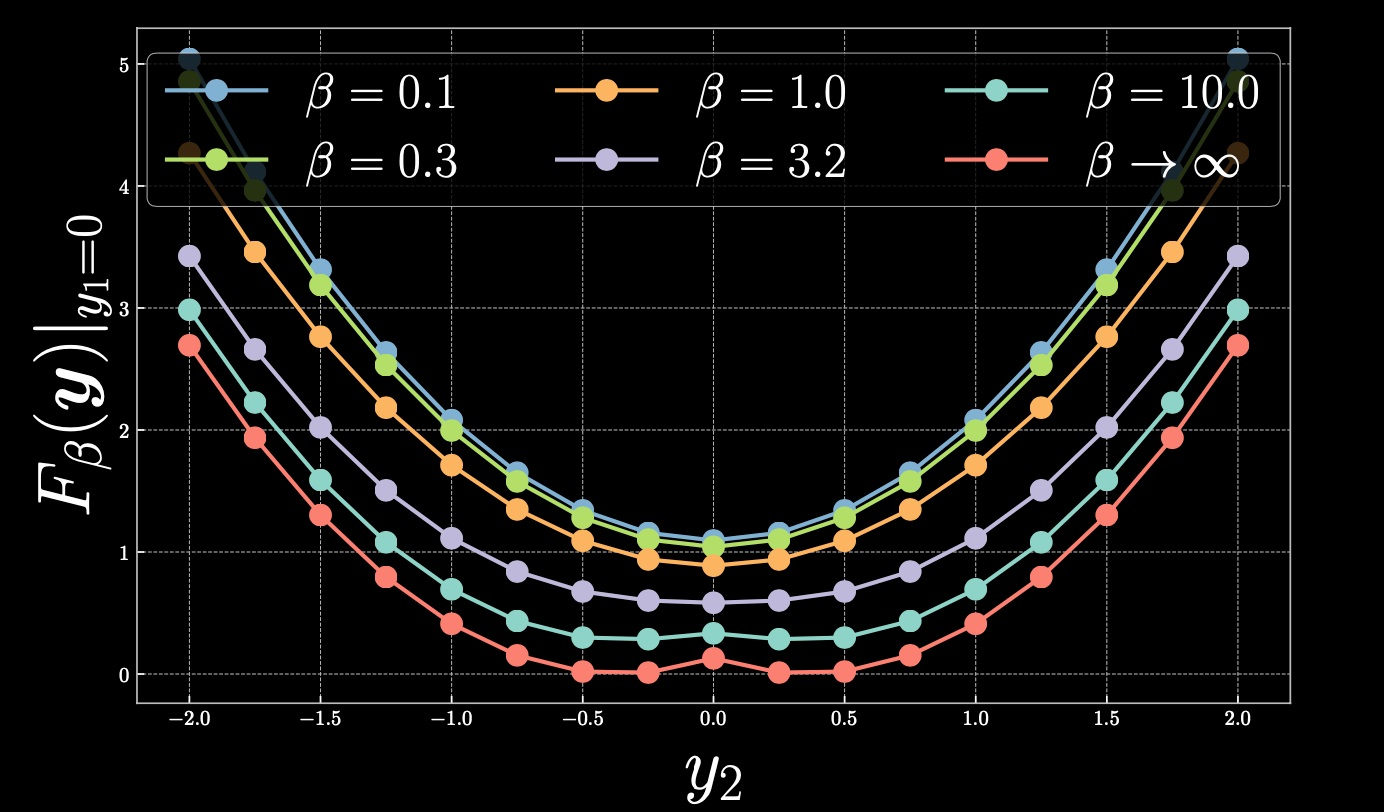
Figure 6 : Résutats en faisant varier le beta

Lorsque nous augmentons la température en réduisant les $\beta$, le résultat est une parabole avec un seul minimum global. Lorsque $\beta$ s’approche de 0, on se retrouve avec la moyenne et on récupère la MSE.

Nomenclature et PyTorch

Formellement, nous définissons le softmax réel comme :

\[\smash{\underset{z}{\text{softmax}}}_\beta[E(y,z)] \doteq \frac{1}{\beta} \log \underset{z\in\mathcal{Z}}{\sum} \exp[{\beta}E(\vect{y},z)] - \frac{1}{\beta} \log{N_z}\]

où $N_z = \vert\mathcal{Z}\vert / \Delta z$.

Pour implémenter la fonction ci-dessus dans PyTorch, nous utilisons torch.logsumexp comme ci-dessous :

\[\smash{\underset{z}{\text{softmax}}}_\beta[E(y,z)] \doteq \frac{1}{\beta} \texttt{torch.logsumexp}({\beta}E(\vect{y},z),\texttt{dim=}z) - \frac{1}{\beta} \log{N_z}\]

Le softmin réel :

\[\smash{\underset{z}{\text{softmin}}}_\beta[E(y,z)] \doteq -\frac{1}{\beta}\log\frac{1}{N_z}\underset{z\in\mathcal{Z}}{\sum}\exp[-{\beta}E(\vect{y},z)]\]

Softmin peut être implémenté en utilisant softmax avec 2 signes négatifs comme suit :

\[\smash{\underset{z}{\text{softmin}}}_\beta[E(y,z)] = -\smash{\underset{z}{\text{softmax}}}_\beta[-E(y,z)]\] \[\texttt{torch.softmax}(l(j),\texttt{dim=j}) = \smash{\underset{j}{\text{softargmax}_{\beta=1}}}[l(j)]\]

En termes techniques, si l’énergie libre est :

• brûlante, cela fait référence à la moyenne.
• chaude, cela se réfère à la marginalisation de la latente.
• froide, cela se réfère à la valeur minimale.

Entraînement des EBMs

Objectif : trouver une fonction d’énergie avec un bon comportement.

Une perte fonctionnelle, minimisée lors de l’apprentissage, est utilisée pour mesurer la qualité des fonctions d’énergie disponibles. En termes simples, la perte fonctionnelle est une fonction scalaire qui nous indique la qualité de notre fonction d’énergie. Il convient de faire la distinction entre la fonction d’énergie, qui est minimisée par le processus d’inférence et la perte fonctionnelle qui est minimisée par le processus d’apprentissage.

\[\mathcal{L}(F(\cdot),Y) = \frac{1}{N} \sum_{n=1}^{N} l(F(\cdot),\vect{y}^{(n)}) \in \R\]

$\mathcal{L}$ est la fonction de perte de l’ensemble des données qui peut être exprimée comme la moyenne de ces fonctions de perte par échantillon.

\[l_{\text{energy}}(F(\cdot),\check{\vect{y}}) = F(\check{\vect{y}})\]

où $l_\text{energy}$ est la fonction de perte d’énergie évaluée en $\vect{y}$ et $\vect{y}$ est le point de données sur l’ensemble de données. $\check{\vect{y}}$ indique les points de données qui doivent être poussés vers le bas. Cela signifie que les pertes de fonctions doivent être réduites au minimum pendant l’entraînement.

La fonction d’énergie doit être petite pour les données qui proviennent de la distribution d’entraînement mais grande ailleurs.

\[l_{\text{hinge}}(F(\cdot),\check{\vect{y}},\hat{\vect{y}}) = \big(m - [F(\hat{\vect{y}})-F(\check{\vect{y}})]\big)^{+}\]

où $m$ est la marge et $F(\check{\vect{y}})$ et $F(\hat{\vect{y}})$ sont les énergies libres pour les énergies froides (pour les étiquettes correctes) et chaudes (pour les étiquettes incorrectes) respectivement.

Le modèle essaie de faire en sorte que la différence entre deux énergies soit supérieure à la marge $m$.

Il existe une fonction ReLU $[\cdot]^{+}$ utilisée sur la sortie de $m - [F(\hat{\vect{y}}) - F(\check{\vect{y}})]$, ce qui signifie que la valeur de cette fonction de perte hinge sera toujours non négative. Cela implique que s’il y a des valeurs négatives, elles deviendront nulles en raison de cette fonction.

L’entraînement rend le terme $F(\hat{\vect{y}}) - F(\check{\vect{y}})$ égal ou supérieur à $m$. Si la différence devient supérieure à $m$, la valeur globale de $[m - [F(\hat{\vect{y}}) - F(\check{\vect{y}})]]$ devient négative, la perte hinge devient nulle. On peut aussi dire que nous poussons les énergies tant que la différence est inférieure à $m$. Cependant, si la différence devient supérieure à la marge $m$, nous cessons de pousser. La fonction de perte hinge n’a pas une marge lisse.

La fonction de perte logarithme a une marge lisse, comme indiqué ci-dessous :

\[l_{\log}(F(\cdot),\check{\vect{y}},\hat{\vect{y}}) = \log(1+\exp[F(\check{\vect{y}})-F(\hat{\vect{y}})])\]

Comme nous avons une fonction exponentielle, cette perte a une marge plus lisse. En d’autres termes, elle semble être une version « douce » de la perte hinge avec une marge infinie.

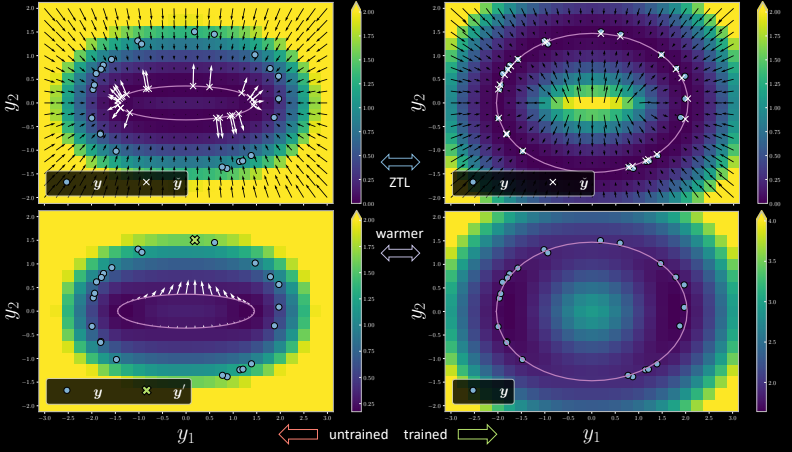
Figure 7

Le côté gauche est la version non entraînée où, pour chaque point d’entraînement, il y a un $x$ correspondant qui est, sur la surface du modèle, l’emplacement le plus proche du point d’entraînement. Pendant l’entraînement à la ZTL (Zero Temperature Limit), le gradient fait que le point de données sur la variété qui est le plus proche du point d’entraînement est poussé vers ce dernier. On peut voir qu’après une époque, la version entraînée du modèle montre les points $x$ arriver à l’endroit désiré. L’énergie passe à zéro correspondant ainsi aux points d’entraînement (points bleus dans la figure).

Lorsque le modèle est entraîné à la ZTL et que la température est augmentée, les points sont choisis individuellement pour être poussés vers le point d’entraînement. Cependant, en cas de marginalisation, si nous choisissons un point $\vect{y}$ (le point vert en croix sur l’image en bas à gauche), le gradient est juste la moyenne de toutes les flèches pointant vers ce point particulier $\vect{y}$). Tous les points sont tirés vers $\vect{y}$, en s’assurant que cela ne surcharge pas les données d’entraînement. La version entraînée ne s’adapte pas à tous les points d’entraînement.

Pour la ZTL (${\beta = {\infty}}$), nous pouvons voir que l’énergie libre a un pic élevé. Au fur et à mesure que nous diminuons ${\beta}$, le pic continue à diminuer et nous le réduisons jusqu’à obtenir ce graphique parabolique lisse en bleu, qui est le graphique en cas de marginalisation.

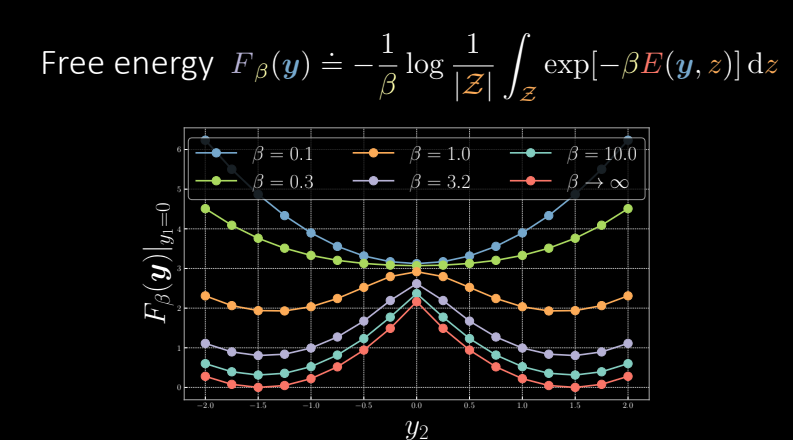
Figure 8 : Energie libre \[F_{\beta}(\vect{y}) \dot{=} -\frac{1}{\beta}\log\frac{1}{\vert\mathcal{Z}\vert}\int_\mathcal{Z}\exp[-{\beta}E(\vect{y},z)]\mathrm{d}z\]

Apprentissage autosupervisé

Une révision des données d’entraînement :

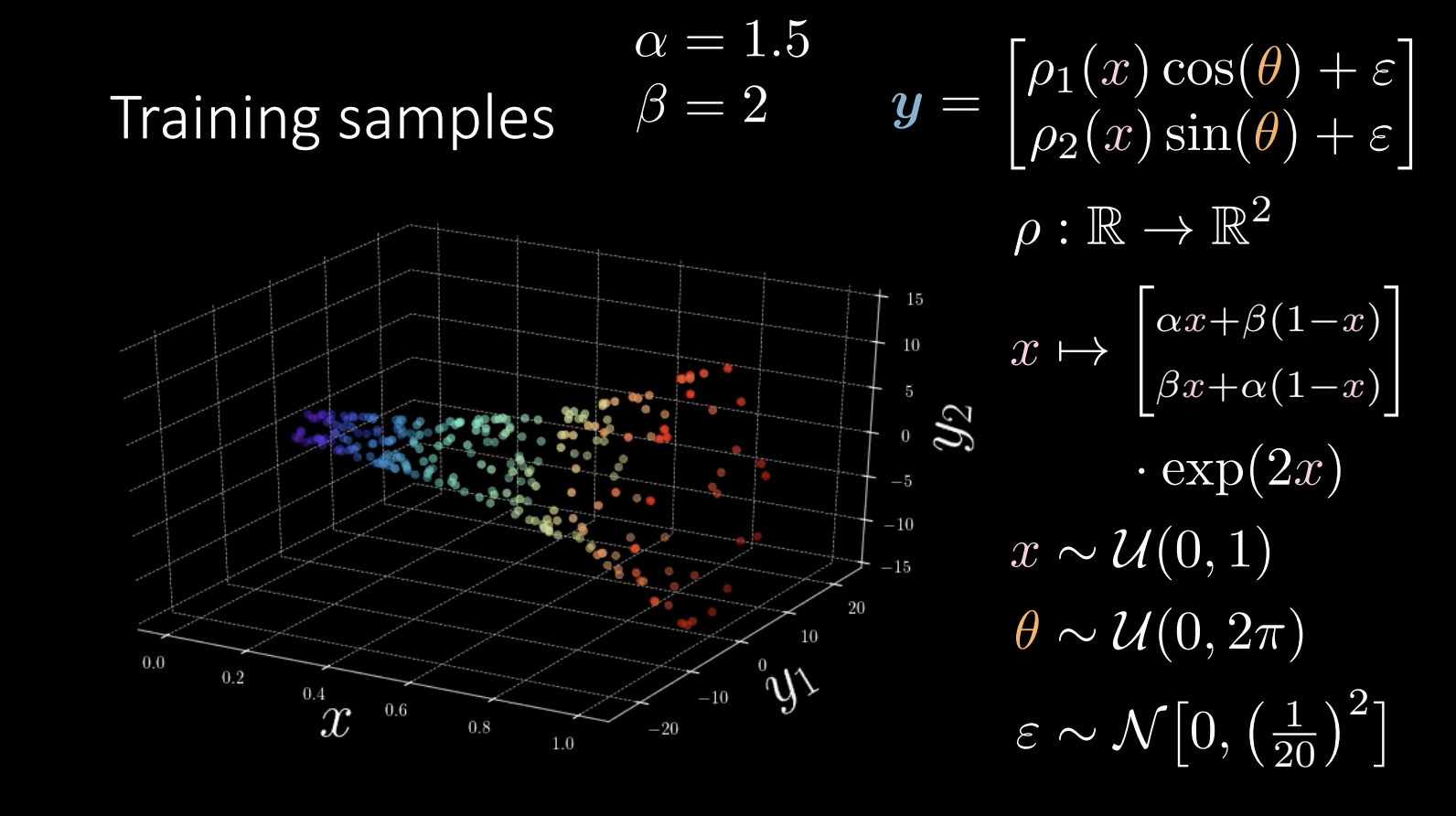
Figure 9 : Données d’entraînement

Pendant l’entraînement, nous essayons d’apprendre la forme de la « corne ».

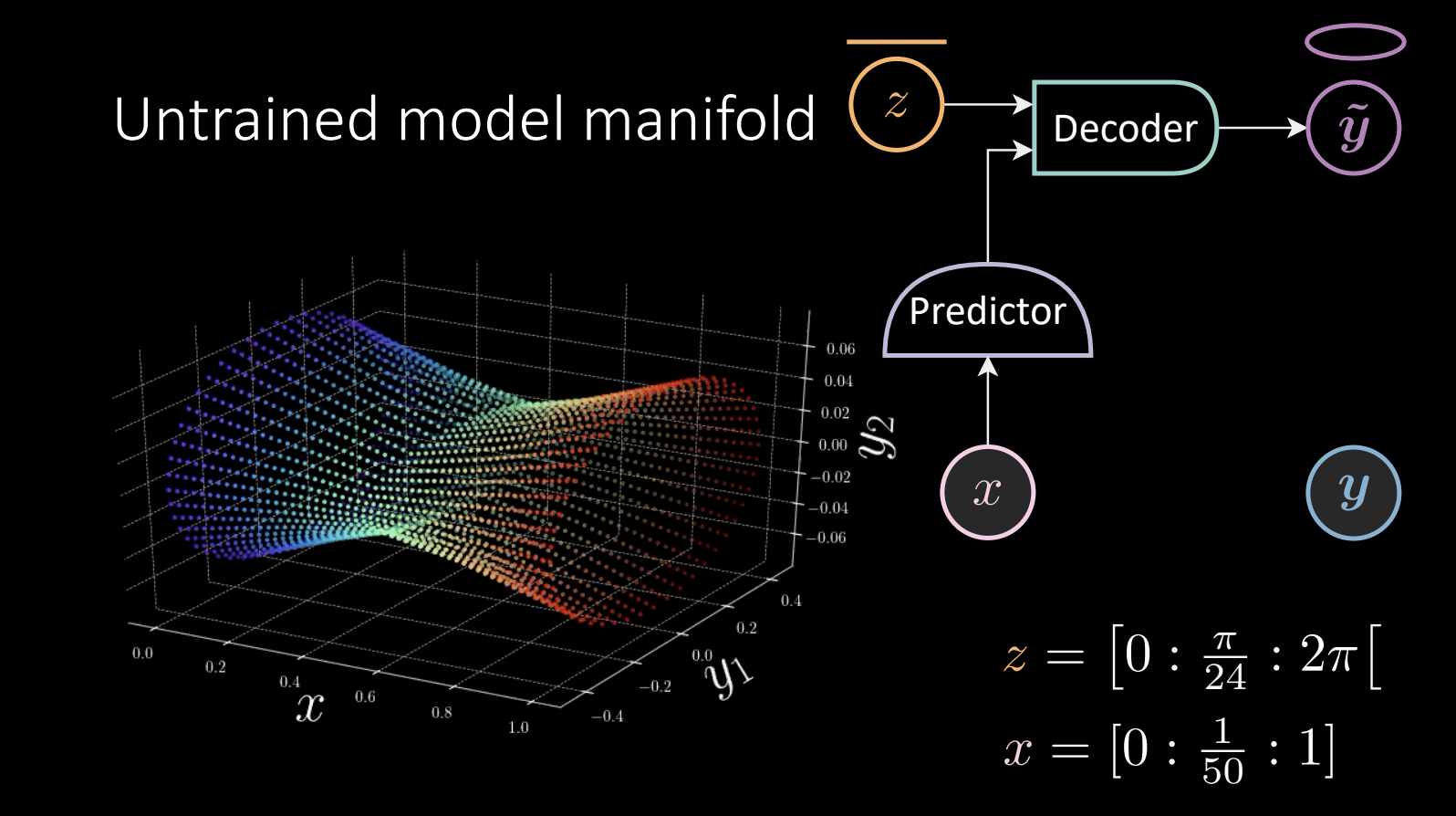
Figure 10 : Variété du modèle non entraîné

$z = [0:\frac{\pi}{24} : 2\pi[$ prend des valeurs de façon linéaire et est introduit dans le décodeur pour obtenir $\tilde{\vect{y}}$, qui va faire le tour de l’ellipse.

Le prédicteur prend le $x$ observé ($x = [0:\frac{1}{50} :1]$) et donne le résultat au décodeur. Nous effectuons un entraînement de l’énergie sans température zéro, ce qui donne un résultat :

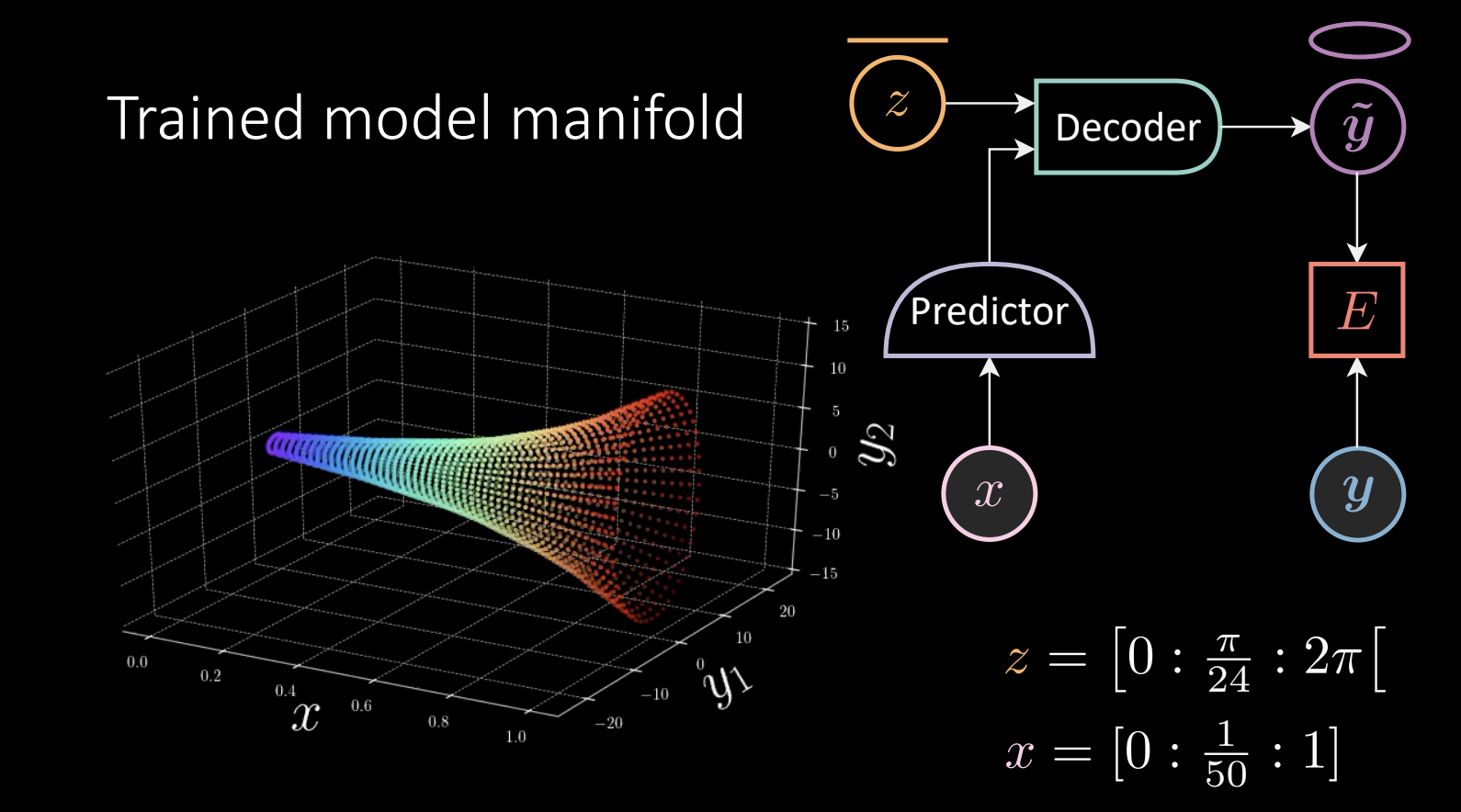
Figure 11 : Variété du modèle entraîné

Compte tenu de la « corne », nous prenons un point $\vect{y}$, trouvons le point le plus proche sur la surface et le tirons vers $\vect{y}$. Dans ce cas, la fonction d’énergie est définie comme \(E(x,\vect{y},z) = [\vect{y}_{1} - f_{1}(x)g_{1}(z)]^{2} + [\vect{y}_{2} -f_{2}(x)g_{2}(z)]^{2}\) où

\[f,g:\mathbb{R} \rightarrow \mathbb{R}^{2}\] \[\begin{array}{l} x \stackrel{f}{\mapsto} x \stackrel{\mathrm{L}^{+}}{\rightarrow} 8 \stackrel{\mathrm{L}^{+}}{\rightarrow} 8 \stackrel{\mathrm{L}}{\rightarrow} 2 \\ z \stackrel{g}{\mapsto}[\cos (z) \quad \sin (z)]^{\top} \end{array}\]

La composante de $g$ sera mise à l’échelle par la sortie de $f$.

L’entraînement des données de l’exemple ne prend pas de temps, mais comment généraliser ?

\[\begin{array}{l} f: \mathbb{R} \rightarrow \mathbb{R}^{\operatorname{dim}(f)} \\ g: \mathbb{R}^{\operatorname{dim}(f)} \times \mathbb{R} \rightarrow \mathbb{R}^{2} \end{array} \\ E(x, \vect{y}, z)=\left[\vect{y}_{1}-g_{1}(f(x), z)\right]^{2}+\left[\vect{y}_{2}-g_{2}(f(x), z)\right]^{2}\]

Dans ce cas, la fonction $g$ prend $f$ et $z$. $g$ peut être un réseau neuronal. Cette fois, le modèle doit apprendre que $\vect{y}$ se déplace en cercle, ce qui est la partie $\sin$ et $\cos$ que nous considérons comme allant de soi auparavant.

Un autre problème consiste à déterminer la dimension de la variable latente $z$.

\[\begin{array}{l} f: \mathbb{R} \rightarrow \mathbb{R}^{\operatorname{dim}(f)} \\ g: \mathbb{R}^{\operatorname{dim}(f)} \times \mathbb{R}^{\operatorname{dim}(z)} \rightarrow \mathbb{R}^{2} \end{array}\\ E(x, \vect{y}, z)=\left[\vect{y}_{1}-g_{1}(f(x), z)\right]^{2}+\left[\vect{y}_{2}-g_{2}(f(x), z)\right]^{2}\]

Puisqu’une haute dimension latente entraîne un surentraînement, nous devons régulariser $z$. Sinon, le modèle mémorisera tous les points, ce qui fera que l’énergie sera nulle dans tout l’espace.

---

📝 Anu-Ujin Gerelt-Od, Sunidhi Gupta, Bichen Kou, Binfeng Xu
Loïck Bourdois
31 Oct 2020