Techniques d’optimisation I

Descente de gradient

Nous commençons notre étude des méthodes d’optimisation par la méthode la plus élémentaire et la pire du lot (raisonnement à suivre) : la méthode de la descente de gradient.

Problème :

Solution itérative :

où :

• $w_{k+1}$ est la valeur mise à jour après la $k$-ème itération,
• $w_k$ est la valeur initiale avant la $k$-ème itération,
• $\gamma_k$ est la taille du pas,
• $\nabla f(w_k)$ est le gradient de $f$.

On suppose ici que la fonction $f$ est continue et différenciable. Notre objectif est de trouver le point le plus bas (vallée) de la fonction d’optimisation. Cependant, la direction réelle de cette vallée n’est pas connue. Nous ne pouvons regarder que localement et de ce fait la direction du gradient négatif est la meilleure information dont nous disposons. Faire un petit pas dans cette direction ne peut que nous rapprocher du minimum. Une fois que nous avons fait ce petit pas, nous calculons à nouveau le gradient et nous nous déplaçons un peu dans cette direction. Nous répétons le processus jusqu’à ce que nous atteignions la vallée. Par conséquent, la descente de de gradient ne fait essentiellement que suivre la direction de la descente la plus raide (pente négative).

Le paramètre $\gamma$ dans l’équation de mise à jour itérative est appelé la taille du pas. En général, nous ne connaissons pas la valeur optimale de la taille de pas. Nous devons donc essayer différentes valeurs. La pratique courante consiste à essayer un ensemble de valeurs sur une échelle logarithmique et à sélectionner la meilleure. Quelques scénarios différents peuvent se produire. L’image ci-desosus représente ces scénarios pour une fonction quadratique 1D. Si le taux d’apprentissage est trop faible, alors nous progresserons régulièrement vers le minimum. Cependant, cela prend plus de temps que ce qui est idéal. Il est généralement très difficile (ou impossible) d’obtenir une échelle qui nous mène directement au minimum. L’idéal serait d’avoir une taille de pas un peu plus grande que l’optimale. En pratique, cela permet d’obtenir la convergence la plus rapide. Cependant, si nous utilisons un taux d’apprentissage trop élevé, les itérations s’éloignent de plus en plus des minima et nous obtenons une divergence. Dans la pratique, nous voudrions utiliser un taux d’apprentissage qui est juste un peu plus petit que celui qui va diverger.

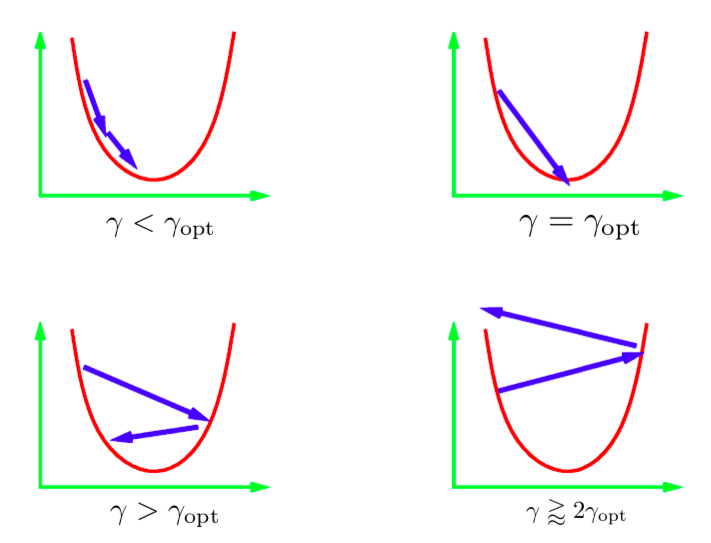
Figure 1 : Différentes valeurs de pas appliquées à une fonction quadratique 1D

Descente de gradient stochastique

Dans le cas de la descente de gradient stochastique (SGD en anglais pour Stochastic Gradient Descent), nous remplaçons le vecteur de gradient réel par une estimation stochastique du vecteur de gradient. Pour un réseau de neurones, l’estimation stochastique signifie le gradient de la perte pour un seul point de données (une seule instance).

Soit $f_i$ qui désigne la perte du réseau pour la $i$-ième instance :

La fonction que nous voulons minimiser est $f$, la perte totale dans tous les cas :

Dans la SGD, nous mettons à jour les poids en fonction du gradient sur $f_i$ (par opposition au gradient sur la perte totale $f$) avec :

Si $i$ est choisi au hasard, alors $f_i$ est un estimateur bruyant mais non biaisé de $f$, qui s’écrit mathématiquement comme :

Par conséquent, le $k$-ème pas prévu de la SGD est le même que le $k$-ème pas de la descente de gradient complète :

Ainsi, toute mise à jour de la SGD est la même que la mise à jour attendue pour la GD à batch complet. Cependant, la SGD n’est pas seulement une descente plus rapide avec du bruit. En plus d’être plus rapide, la SGD peut également nous donner de meilleurs résultats que la descente de gradient avec batch complet. Le bruit dans la SGD peut nous aider à éviter les minima locaux peu profonds et à trouver de meilleurs minima (plus profonds). Ce phénomène est appelé annealing.

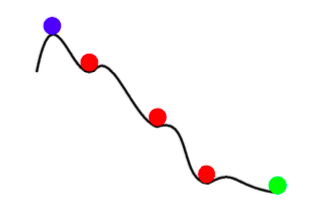
Figure 2 : Annealing avec la SGD

En résumé, les avantages de la descente de gradient stochastique sont les suivants :

1. Il y a beaucoup d’informations redondantes d’une instance à l’autre. La SGD empêche beaucoup de ces calculs redondants.
2. Aux premiers stades, le bruit est faible par rapport aux informations dans le gradient. Par conséquent, une étape de SGD est virtuellement aussi bonne qu’une étape de GD.
3. Le bruit dans la mise à jour de la SGD peut empêcher la convergence vers un mauvais minimum local (peu profond).
4. La descente stochastique de gradient est considérablement moins coûteuse à calculer (car on ne passe pas en revue tous les points des données).

Les mini-batchs

Avec les mini-batchs, nous considérons la perte sur plusieurs instances choisies au hasard au lieu de la calculer sur une seule instance. Cela permet de réduire le bruit lors de la mise à jour des étapes :

Souvent, nous pouvons faire un meilleur usage de nos capacités de calcul en utilisant des mini-batchs au lieu d’une seule instance. Par exemple, les GPUs sont mal utilisés lorsque nous effectuons un entraînement avec une seule instance. Les techniques d’entraînement en réseau distribué répartissent les mini-batchs entre les différentes machines et agrègent ensuite les gradients résultants. En utilisant une telle distribution, Facebook a récemment entraîné un réseau sur les données d’ImageNet en moins d’une heure (Goyal et al. (2018)). Il est important de noter que la descente de gradient ne doit jamais être utilisée avec des batchs de taille entière. Si vous souhaitez faire cela utilisez plutôt une technique d’optimisation appelée LBFGS. PyTorch et SciPy fournissent tous deux des implémentations de cette technique.

Momentum

Avec momentum, nous avons deux itérations ($p$ et $w$) au lieu d’une seule. Les mises à jour sont les suivantes :

$p$ est appelé le momentum da la SGD. À chaque étape de la mise à jour, nous ajoutons le gradient stochastique à l’ancienne valeur du momentum, après l’avoir amorti d’un facteur $\beta$ (valeur comprise entre 0 et 1). On peut considérer $p$ comme une moyenne mobile des gradients. Enfin, nous déplaçons $w$ dans la direction du nouvel élan $p$.

Forme alternative : la « méthode stochastique de la boule lourde »

Cette formule est mathématiquement équivalent à la précédente. Ici, l’étape suivante est une combinaison de la direction de l’étape précédente ($w_k - w_{k-1}$) et du nouveau gradient négatif.

Intuition

La SGD momentum est similaire au concept d’élan en physique. Le processus d’optimisation ressemble à une balle lourde qui dévale la colline. Momentum maintient la balle dans la même direction que celle dans laquelle elle se déplace déjà. Le gradient peut être considéré comme une force poussant la balle dans une autre direction.

Figure 3 : Effet du momentum - Source : distill.pub

Plutôt que de changer radicalement la direction du déplacement (comme dans la figure de gauche), momentum apporte des changements modestes. Il amortit les oscillations qui sont courantes lorsque nous n’utilisons que la SGD.

Le paramètre $\beta$ est appelé le facteur d’amortissement. $\beta$ doit être supérieur à zéro, car s’il est égal à zéro, on ne fait qu’une descente de gradient. Il doit également être inférieur à 1, sinon tout explose. Des valeurs plus petites de $\beta$ entraînent un changement de direction plus rapide. Pour des valeurs plus élevées, il faut plus de temps pour « tourner ».

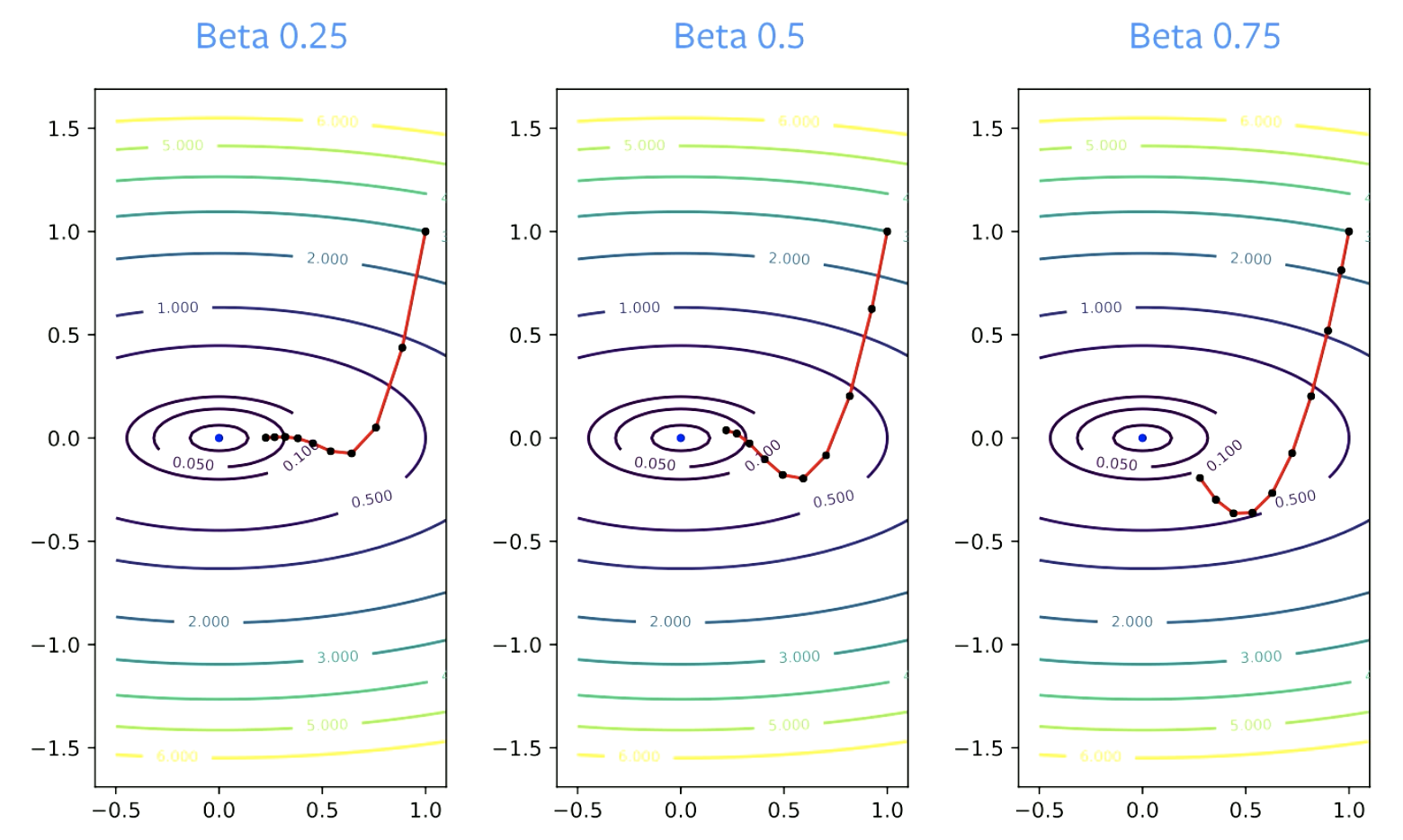
Figure 4 : Effet du bêta sur la convergence

Informations pratiques

Le momentum doit presque toujours être utilisé avec une descente de gradient stochastique. $\beta$ = 0,9 ou 0,99 fonctionne presque toujours bien.

La valeur du pas doit généralement être diminuée lorsque le paramètre de momentum est augmenté pour maintenir la convergence. Si $\beta$ passe de 0,9 à 0,99, le taux d’apprentissage doit être diminué d’un facteur 10.

Comment fonctionne le momentum ?

Accélération

Voici les règles de mise à jour pour le momentum de Nesterov :

Avec le momentum de Nesterov, il est possible d’obtenir une convergence accélérée en choisissant les constantes très soigneusement. Cependant cela ne s’applique qu’aux problèmes convexes et non aux réseaux de neurones.

Beaucoup de gens disent que le momentum normal est une méthode accélérée. Mais en réalité, elle n’est accélérée que pour les fonctions quadratiques. De plus, l’accélération ne fonctionne pas bien avec la SGD, car la SGD a du bruit or l’accélération ne fonctionne pas bien avec le bruit. Par conséquent, bien qu’une certaine accélération soit présente avec la SGD momentum, elle ne suffit pas à expliquer les performances élevées de la technique.

Lissage du bruit

Une raison plus pratique et plus probable pour laquelle le momentum fonctionne est probablement le lissage du bruit. Le momentum est une moyenne mobile des gradients que nous utilisons pour chaque étape de mise à jour. Théoriquement, pour que la SGD fonctionne, nous devrions prendre la moyenne de toutes les mises à jour par étapes : \(\bar w_k = \frac{1}{K} \sum_{k=1}^K w_k\)

L’avantage avec la SGD avec momentum est que cette moyenne n’est plus nécessaire. Le momentum ajoute un lissage au processus d’optimisation, ce qui fait de chaque mise à jour une bonne approximation de la solution. Avec la SGD, on voudrait faire la moyenne de tout un tas de mises à jour et ensuite faire un pas dans cette direction. L’accélération et le lissage du bruit contribuent tous deux à la performance élevée du momentum.

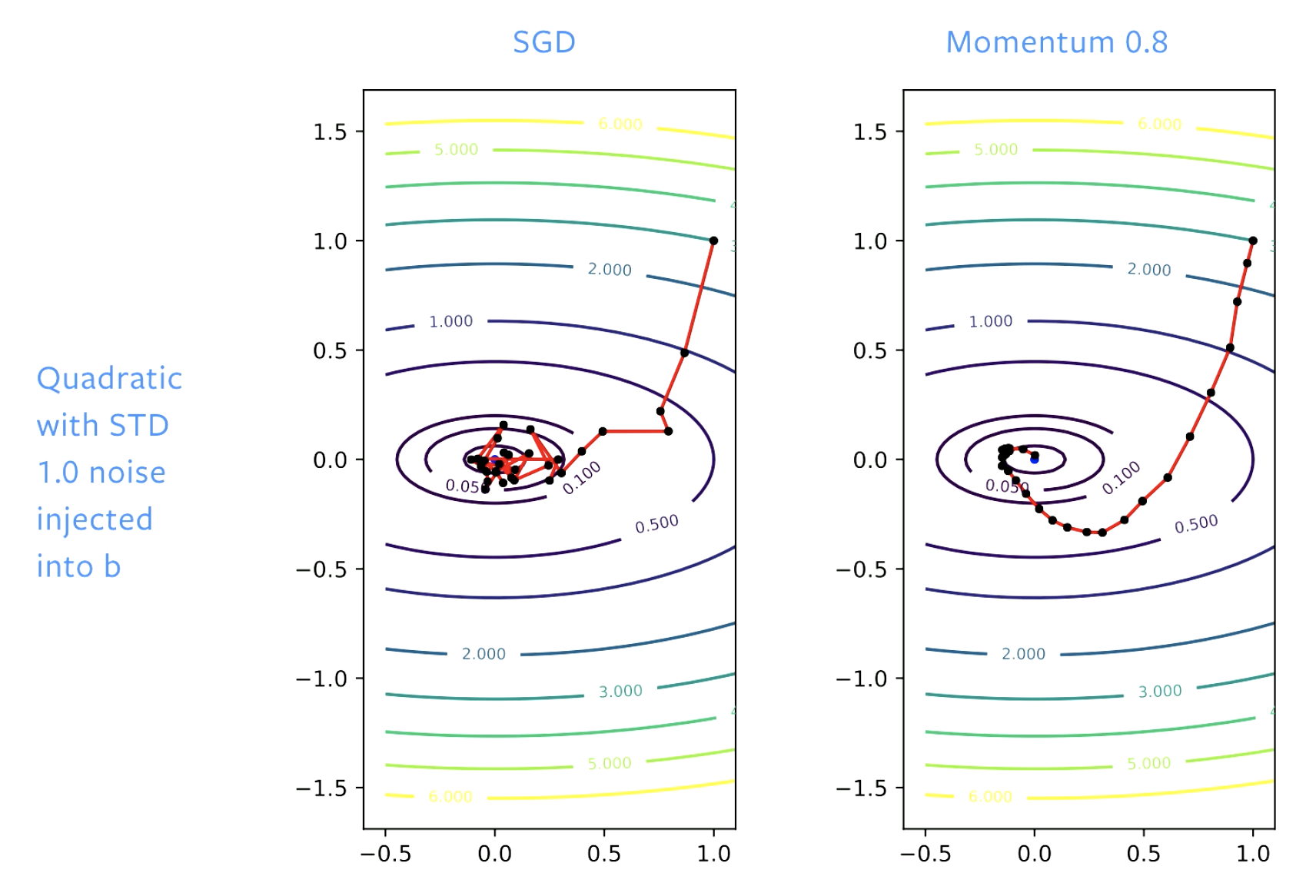
Figure 5 : SGD vs Momentum

Avec la SGD, nous progressons bien vers une solution au départ, mais lorsque nous atteignons le fond de la vallée, nous rebondissons. Si nous ajustons le taux d’apprentissage, nous rebondissons plus lentement. Avec le momentum, nous lissons les étapes, de sorte qu’il n’y a pas de rebondissement.