Surentraînement et régularisation

Surentraînement

Considérez un problème de régression. Un modèle peut être sousentraîné, bien entraîné ou surentraîné.

Si le modèle n’est pas suffisamment expressif pour les données, il sera sousentraîné. Si le modèle est plus expressif que les données (comme c’est le cas pour les réseaux neuronaux profonds), il risque de surentraîner.

Dans ce cas, le modèle est suffisamment puissant pour s’adapter à la fois aux données d’origine et au bruit, ce qui produit une mauvaise solution pour la tâche à accomplir.

Dans l’idéal, nous aimerions que notre modèle s’adapte aux données sous-jacentes et non au bruit, ce qui produirait un bon entraînement de nos données. Nous aimerions surtout le faire sans avoir besoin de réduire la puissance de nos modèles. Les modèles d’apprentissage profond sont très puissants, souvent bien plus que ce qui est strictement nécessaire pour apprendre les données. Nous aimerions conserver cette puissance (pour faciliter l’entraînement) mais tout en luttant contre le surentraînenement.

Surentraînement pour le débogage

Le surentraînement peut être utile dans certains cas, par exemple lors du débogage. On peut tester un réseau sur un petit sous-ensemble de données d’entraînement (même un seul batch ou un ensemble de tenseurs de bruit aléatoire) et s’assurer que le réseau est capable de sur-entraîner sur ces données. S’il ne parvient pas à apprendre, c’est le signe qu’il y a peut-être un bogue.

Régularisation

Nous pouvons essayer de lutter contre le surentraînement en introduisant une régularisation. L’ampleur de la régularisation aura une incidence sur les performances de validation du modèle. Une régularisation trop faible ne résoudra pas le problème du surentraînement. Trop de régularisation rendra le modèle beaucoup moins efficace.

La régularisation ajoute des connaissances préalables à un modèle, une distribution préalable est spécifiée pour les paramètres. Elle agit comme une restriction sur l’ensemble des fonctions pouvant être apprises.

Une autre définition de la régularisation de Ian Goodfellow : « la régularisation est toute modification que nous apportons à un algorithme d’apprentissage visant à réduire son erreur de généralisation mais pas son erreur d’entraînement ».

Techniques d’initialisation

Nous pouvons sélectionner un préalable pour les paramètres de notre réseau en initialisant les poids selon une distribution particulière. Une option : l’initialisation de Xavier.

Régularisation du taux de décroissance des poids

Le taux de décroissance des poids (weight decay) est notre première technique de régularisation. Elle est largement utilisée dans l’apprentissage machine, mais moins dans les réseaux de neurones. Dans PyTorch, cela est fourni comme paramètre à l’optimiseur (voir par exemple le paramètre weight_decay pour SGD).

Ce paramètre est également appelé :

• L2
• Ridge
• Gaussian prior

On peut envisager un objectif qui agit sur les paramètres :

puis nous avons des mises à jour :

Pour le taux de décroissance des poids, nous ajoutons un terme de pénalité :

qui produit une mise à jour :

Ce nouveau terme dans la mise à jour conduit les paramètres $\theta$ légèrement vers 0, en ajoutant une certaine décroissance dans les poids à chaque mise à jour.

Régularisation L1

Disponible en option pour PyTorch optimiseurs.

Aussi appelé :

• LASSO
• Laplacian prior
• Sparsity prior

En considérant cela comme une distribution de Laplace antérieure, cette régularisation met plus de masse de probabilité près de $0$ que ne le fait une distribution gaussienne.

En commençant avec la même mise à jour que ci-dessus, nous pouvons considérer que cela ajoute une autre pénalité :

qui produit une mise à jour :

Contrairement au taux de décroissance $L_2$, la régularisation $L_1$ « tuera » les composantes qui sont proches d’un axe dans l’espace de paramètres, plutôt que de réduire de manière égale la longueur du vecteur de paramètres.

Dropout

Le dropout consiste à mettre à $0$ un certain nombre de neurones de façon aléatoire pendant l’entraînement. Cela empêche le réseau d’apprendre un chemin singulier de l’entrée à la sortie. De même, en raison de la grande paramétrisation des réseaux de neurones, il est possible pour le réseau de neurones de mémoriser efficacement l’entrée. Cependant, avec le dropout, cela est beaucoup plus difficile car l’entrée est mise dans un réseau différent à chaque fois, puisque le dropout entraîne effectivement un nombre infini de réseaux qui sont différents à chaque fois. Par conséquent, le dropout peut être un moyen efficace de contrôler le surentraînement et d’être plus résistant aux petites variations de l’entrée.

Figure 1 : Réseau sans dropout

Figure 2 : Réseau avec dropout

Dans PyTorch, nous pouvons fixer un taux de dropout aléatoire des neurones.

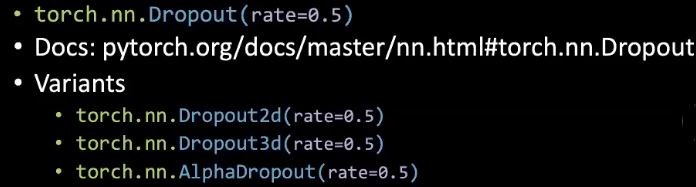
Figure 3 : Code pour le dropout

Après l’entraînement, lors de l’inférence, le dropout n’est plus utilisé. Afin de créer le réseau final pour l’inférence, nous faisons la moyenne de tous les réseaux individuels créés pendant le dropout et nous l’utilisons pour l’inférence. Nous pouvons également multiplier tous les poids par $1/(1-p)$, où $p$ est le taux de dropout.

Arrêt anticipé

Pendant l’entraînement, si la perte de validation commence à augmenter, nous pouvons arrêter l’entraînement et utiliser les meilleurs poids trouvés jusqu’à présent. Cela permet d’éviter que les poids n’augmentent trop, ce qui commencerait à nuire aux performances de validation à un moment donné. En pratique, il est courant de calculer la performance de validation à certains intervalles et de s’arrêter après qu’un certain nombre de calculs d’erreurs de validation aient cessé de diminuer.

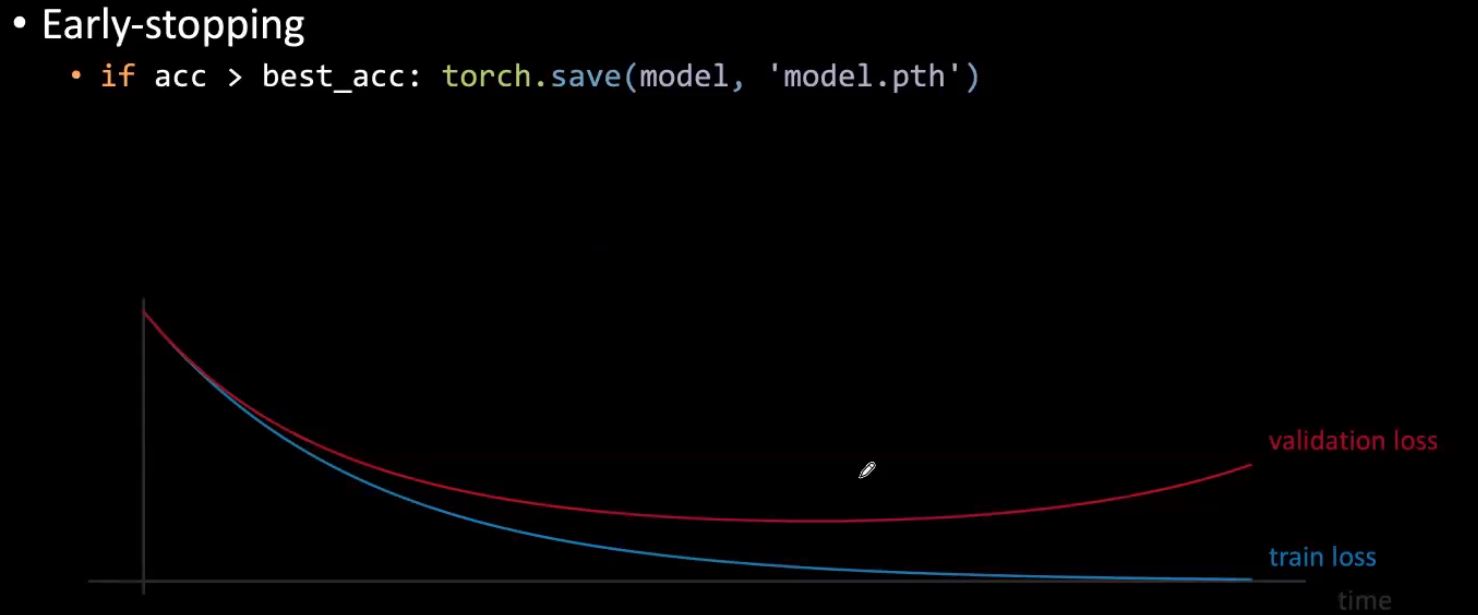
Figure 4 : Arrêt anticipé

Lutter indirectement contre le surentraînement

Il existe des techniques qui ont pour effet secondaire de régulariser les paramètres mais qui ne sont pas elles-mêmes des régulariseurs.

Normalisation par batch

Comment la normalisation par batch rend-elle l’entraînement plus efficace ?

Nous pouvons utiliser un taux d’apprentissage plus élevé lorsque nous appliquons la normalisation par batch. Elle est utilisée pour empêcher le déplacement des covariables internes d’un réseau neuronal, mais la question de savoir si elle permet réellement d’atteindre cet objectif et quel en est le véritable avantage fait l’objet de nombreux débats.

Figure 5 : Batch-normalisation

La normalisation par batch étend essentiellement la logique de normalisation de l’entrée du réseau neuronal à la normalisation de l’entrée de chaque couche cachée du réseau. L’idée de base est d’avoir une distribution fixe qui alimente chaque couche suivante d’un réseau neuronal puisque l’apprentissage se fait mieux lorsque nous avons une distribution fixe. Pour ce faire, nous calculons la moyenne et la variance de chaque batch avant chaque couche cachée et nous normalisons les valeurs entrantes par ces statistiques spécifiques aux batchs, ce qui réduit la quantité par laquelle les valeurs vont finalement se déplacer pendant l’entraînement.

En ce qui concerne l’effet de régularisation, étant donné que chaque batch est différent, chaque échantillon sera normalisé par des statistiques légèrement différentes en fonction du lot dans lequel il se trouve. Ainsi, le réseau verra différentes versions légèrement modifiées d’une même entrée, ce qui l’aidera à apprendre à être plus robuste contre de légères variations de l’entrée et à éviter le surentraînement. Un autre avantage de la batch normalisation est que l’entraînement est beaucoup plus rapide.

Plus de données

La collecte de données supplémentaires est un moyen facile d’éviter le surentraînement mais peut être coûteuse ou impossible.

L’augmentation de données

Les transformations réalisées à l’aide de Torchvision peuvent avoir un effet régulariseur en apprenant au réseau à être insensible aux perturbations.

Figure 6 : L’augmentation de données

L’apprentissage par transfert et le finetuning

L’apprentissage par transfert (TF pour Transfert learning) consiste simplement à entraîner un classifieur final en plus d’un réseau pré-entraîné (utilisé généralement dans les cas où les données sont peu nombreuses).

Le finetuning (FT) consiste à entraîner également des parties partielles ou complètes du réseau pré-entraîné (utilisé dans les cas où nous disposons de beaucoup de données en général).

En général, quand devrions-nous geler les couches d’un modèle pré-entraîné ?

Si nous avons peu de données d’entraînement.

4 cas généraux :

• 1) Si nous avons peu de données avec des distributions similaires, nous pouvons simplement faire un apprentissage par transfert.
• 2) Si nous avons beaucoup de données avec des distributions similaires, nous pouvons faire un finetuning afin d’améliorer également les performances de l’extracteur de caractéristiques.
• 3) Si nous avons peu de données et une distribution différente, nous devrions supprimer quelques couches finales entraînées dans l’extracteur de caractéristiques car elles sont trop spécialisées.
• 4) Si nous avons beaucoup de données et qu’elles proviennent de différentes distributions, nous pouvons simplement entraîner toutes les parties.

A noter que nous pouvons également utiliser des taux d’apprentissage différents pour les différentes couches afin d’améliorer les performances.

Pour approfondir notre discussion sur le surentraînement et la régularisation, examinons les visualisations ci-dessous. Ces visualisations ont été générées avec le code de la version anglaise de ce notebook. Une version en français est disponible ici.

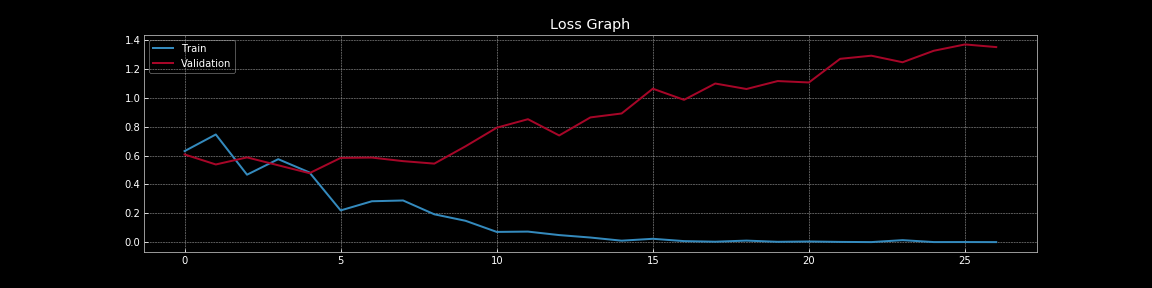
Figure 7 : Courbes de perte sans dropout

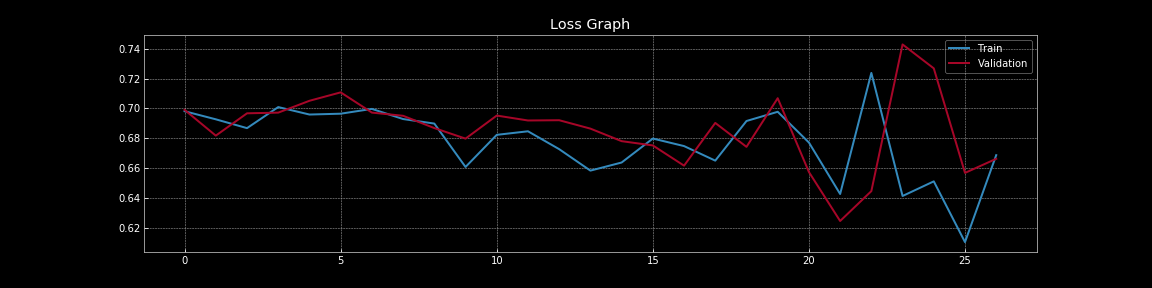
Figure 8 : Courbes de perte avec dropout

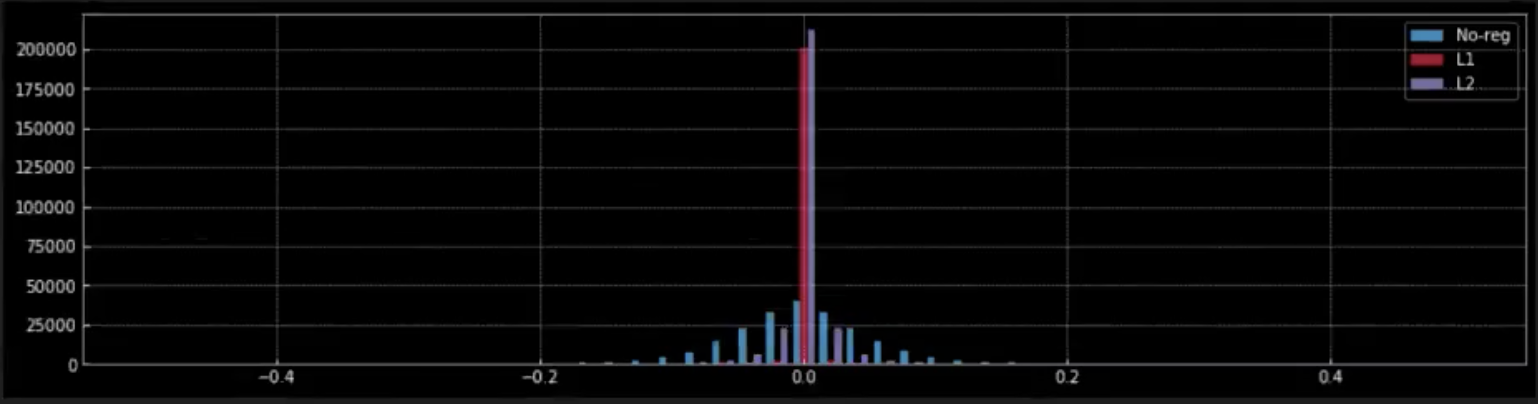
Figure 9 : Effet de la régularisation sur les poids

Les figures 7 et 8 nous permettent de comprendre l’effet spectaculaire que le dropout a sur l’erreur de généralisation, c’est-à-dire la différence entre la perte d’entraînement et la perte de validation. Dans la figure 7 sans dropout, il y a un surentraînement évident car la perte d’entraînement est beaucoup plus faible que la perte de validation. Cependant, dans la figure 8 avec le dropout, la perte d’entraînement et la perte de validation se chevauchent presque continuellement ce qui indique que le modèle se généralise bien à l’ensemble de validation nous servant de substitut pour l’ensemble hors échantillon. Bien entendu, nous pouvons mesurer la performance réelle hors échantillon en utilisant un ensemble de tests de résistance distinct.

Dans la figure 9, nous observons l’effet que la régularisation (L1 et L2) a sur les poids du réseau.

• Lorsque nous appliquons la régularisation L1 à partir du pic rouge à $0$, nous pouvons comprendre que la plupart des poids sont nuls. Les petits points rouges plus proches de $0$ sont les poids non nuls du modèle.

• Par contraste, dans la régularisation L2, à partir du pic violet proche de $0$, nous pouvons voir que la plupart des poids sont proches de $0$ mais non nuls.

• Lorsqu’il n’y a pas de régularisation (bleu), les poids sont beaucoup plus souples et s’étalent autour de $0$ comme dans une distribution normale.

Réseaux de neurones Bayésiens : estimer l’incertitude autour des prévisions

Nous nous soucions de l’incertitude dans les réseaux de neurones car un réseau a besoin de savoir à quel point il est certain/confident de ses prédictions.

Par exemple, si nous construisons un réseau de neurones pour prédire le contrôle de la direction, nous devons connaître le degré de confiance des prédictions du réseau.

Nous pouvons utiliser un réseau de neurones avec dropout pour obtenir un intervalle de confiance autour de nos prédictions. Entraînons un réseau avec dropout, $r$ étant le taux de dropout.

Habituellement, lors de l’inférence, nous mettons le réseau en mode de validation et utilisons tous les neurones pour obtenir la prédiction finale. Tout en faisant la prédiction, nous échelonnons les poids $\delta$ par $\dfrac{1}{1-r}$ pour tenir compte des neurones abandonnés pendant l’entraînement.

Cette méthode nous permet d’obtenir une seule prédiction pour chaque entrée. Cependant, pour obtenir un intervalle de confiance autour de notre prédiction, nous avons besoin de plusieurs prédictions pour la même entrée. Ainsi, au lieu de mettre le réseau en mode validation pendant l’inférence, nous le gardons en mode d’entraînement, c’est-à-dire que nous appliquons toujours le dropout sur des neurones de manière aléatoire et obtenons une prédiction. En faisant plusieurs prédictions pour la même entrée avec ce réseau avec dropout, nous obtenons des prédictions différentes selon les neurones qui sont dropés. Nous utilisons ces prédictions pour estimer la prédiction finale moyenne et un intervalle de confiance autour de celle-ci.

Dans les images ci-dessous, nous avons estimé les intervalles de confiance autour des prédictions des réseaux. Ces visualisations ont été générées avec la version anglaise de ce notebook. Une version en français est disponible ici. La ligne rouge représente les prédictions. La région en violet autour des prédictions représente l’incertitude c’est-à-dire la variance des prédictions.

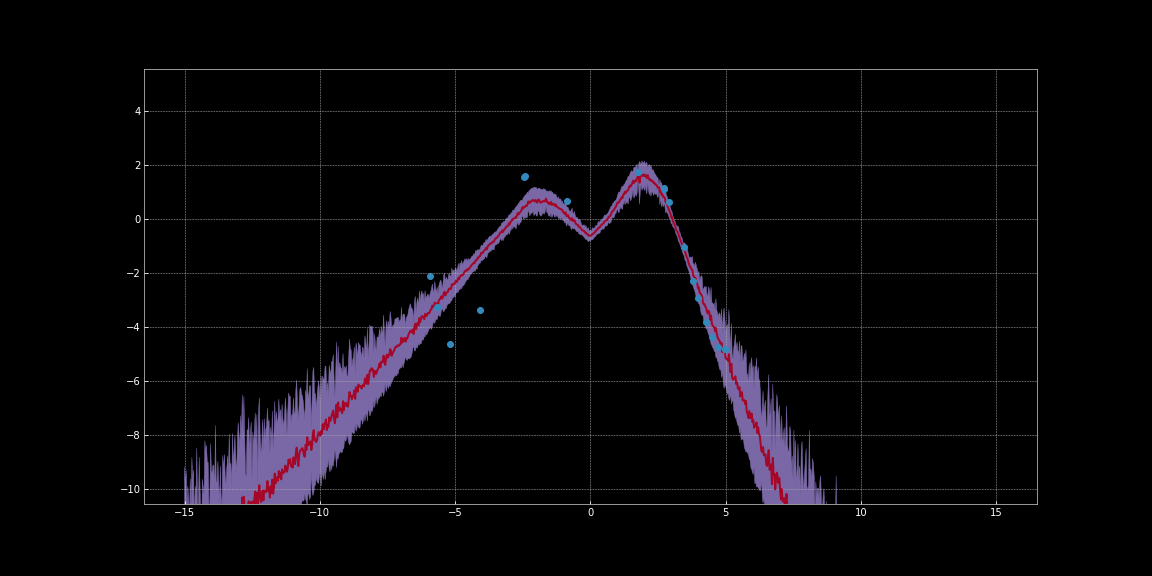
Figure 10 : Estimation de l'incertitude en utilisant l'activation ReLU

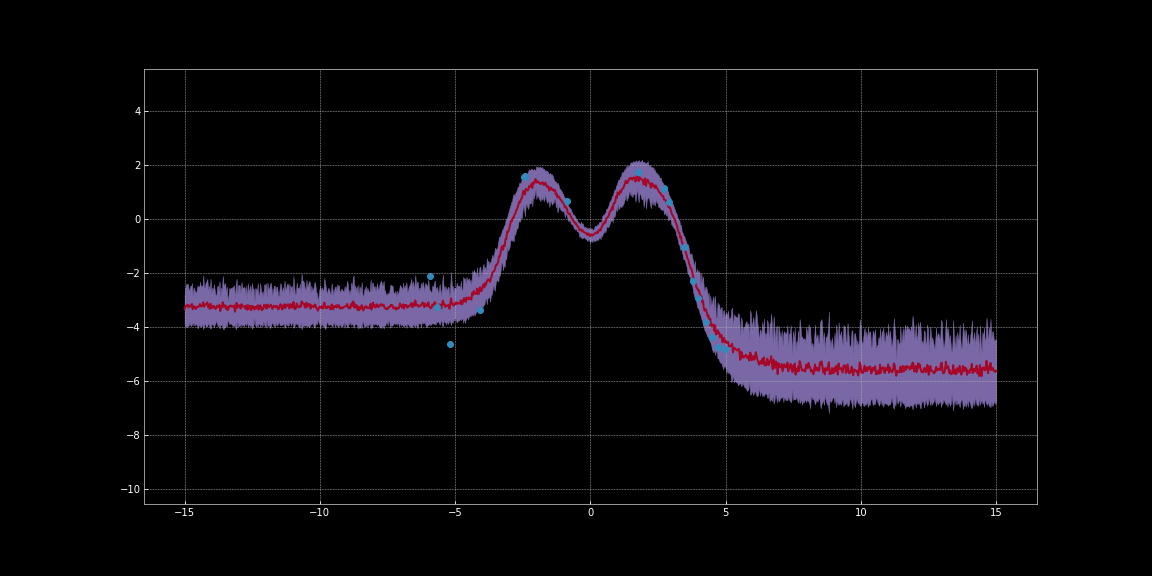
Figure 11 : Estimation de l'incertitude en utilisant l'activation Tanh

Comme vous pouvez l’observer sur les images ci-dessus, ces estimations d’incertitude ne sont pas calibrées. Elles sont différentes pour différentes fonctions d’activation. Sur les images, on remarque que l’incertitude autour des points de données est faible. De plus, la variance que nous pouvons observer est une fonction différentiable. Nous pouvons donc effectuer une descente de gradient pour minimiser cette variance. Nous pouvons ainsi obtenir des prévisions plus fiables.

Si notre EBM comporte plusieurs termes contribuant à la perte totale, comment interagissent-ils ?

Dans les EBMs, nous pouvons simplement et commodément additionner les différents termes pour estimer la perte totale.

Digression : un terme qui pénalise la longueur de la variable latente peut agir comme l’un des nombreux termes de perte dans un modèle. La longueur d’un vecteur est à peu près proportionnelle au nombre de dimensions qu’il possède. Ainsi, si nous diminuons le nombre de dimensions, la longueur du vecteur diminue et par conséquent il code moins d’informations. Dans un paramétrage d’auto-encodeur, cela permet de s’assurer que le modèle conserve les informations les plus importantes. Ainsi, une façon de bloquer l’information dans les espaces latents est de réduire la dimensionnalité de l’espace latent.

Comment déterminer l’hyperparamètre pour la régularisation ?

En pratique, pour déterminer l’hyperparamètre optimal pour la régularisation, c’est-à-dire la force de régularisation, nous pouvons utiliser :

• l’optimisation des hyperparamètres bayésiens
• la recherche par grille
• la recherche aléatoire Lors de ces recherches, les premières époques sont généralement suffisantes pour nous donner une idée du fonctionnement de la régularisation. Nous devons donc entraîner le modèle de façon intensive.