Réseaux de neurones artificiels

🎙️ Alfredo Canziani

Apprentissage supervisé pour la classification

• Considérons la figure 1(a) ci-dessous. Les points de ce graphique se trouvent sur les branches de la spirale et vivent dans $\R^2$. Chaque couleur représente une classe. Le nombre de classes uniques est $K = 3$. Ceci est représenté mathématiquement par l’éqn. 1(a).

• La figure 1(b) montre une spirale similaire, avec un terme de bruit gaussien ajouté. Ceci est représenté mathématiquement par l’éqn. 1(b).

  Dans les deux cas, ces points ne sont pas séparables linéairement.

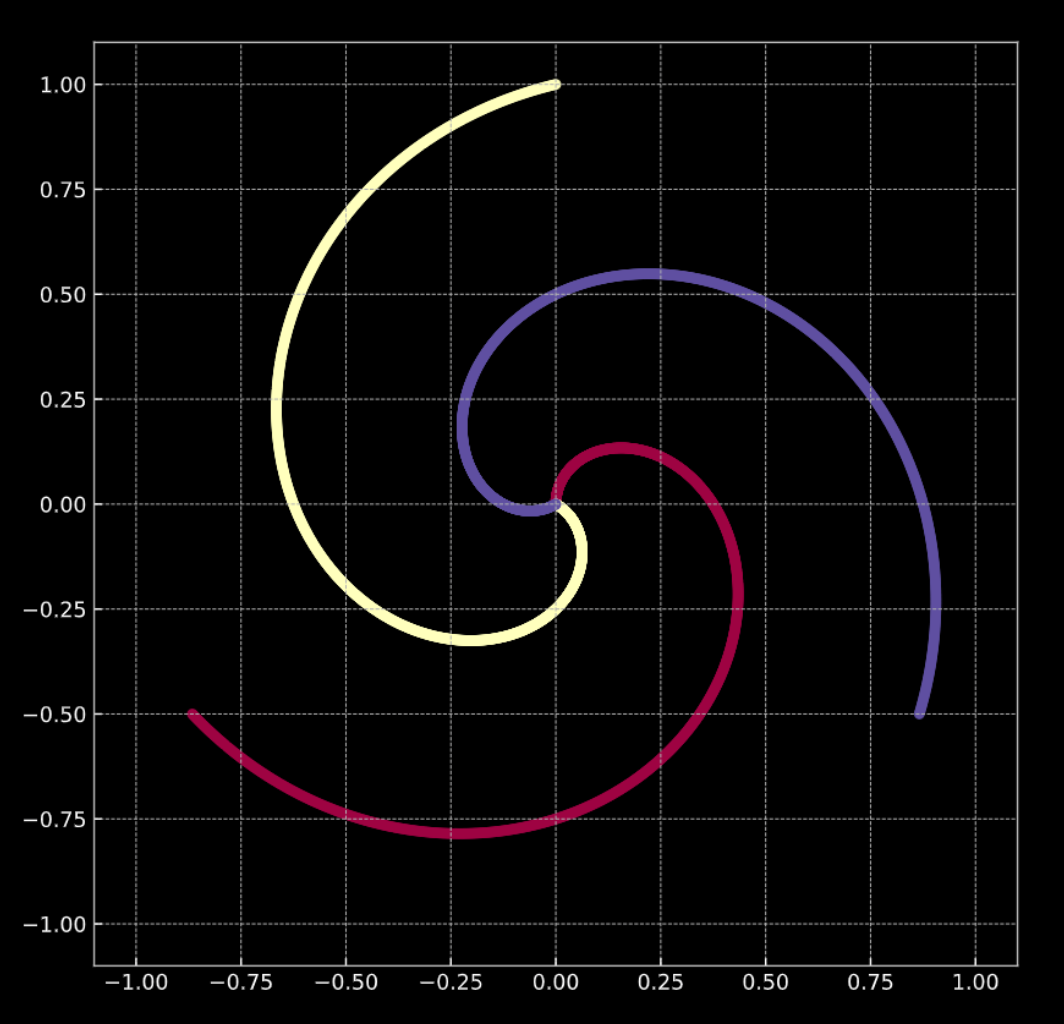
  Figure 1(a) : Spirale 2D « propre »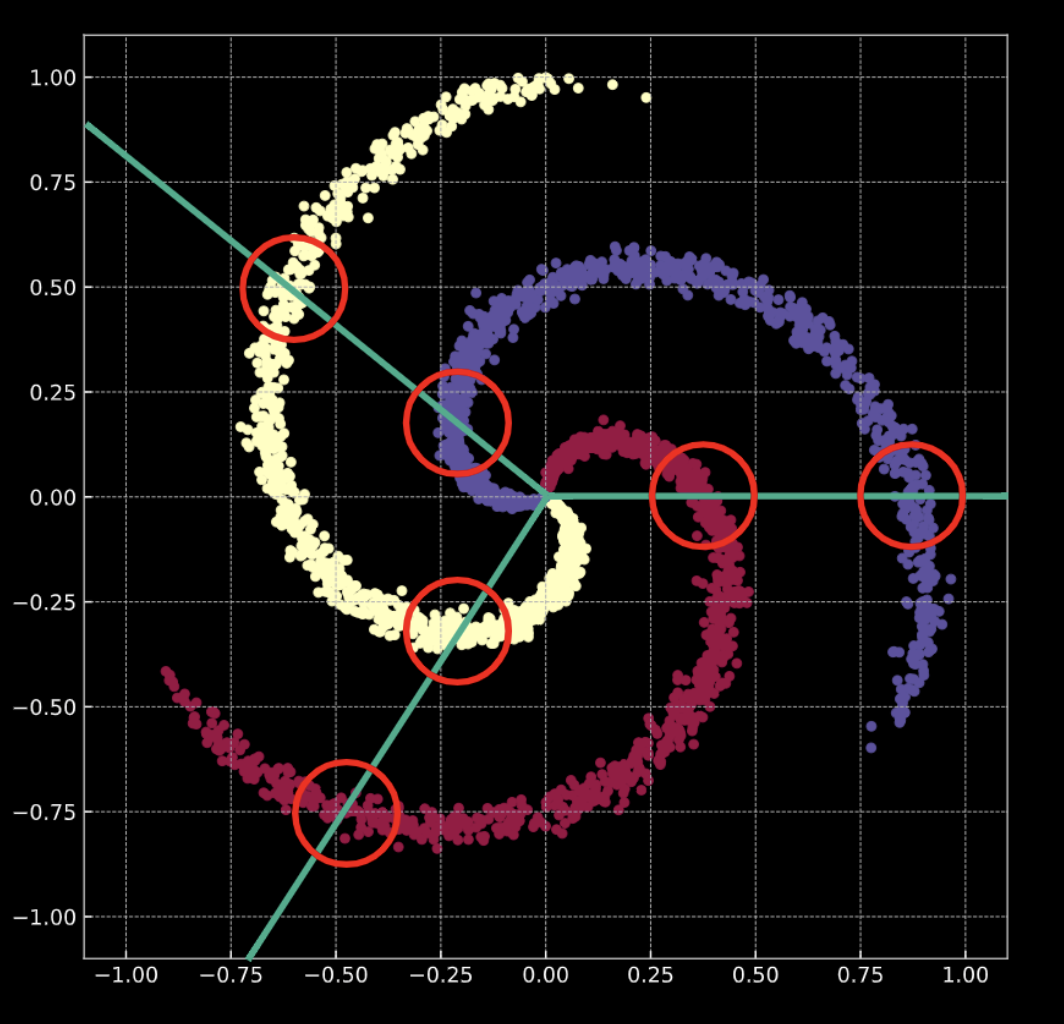

  Figure 1(b) : Spirale 2D « bruyante »

  
  
  

\[X_{k}(t)=t\left(\begin{array}{c}{\sin \left[\frac{2 \pi}{K}(2 t+k-1)\right]} \\ {\cos \left[\frac{2 \pi}{K}(2 t+k-1)\right]}\end{array}\right) \\ 0 \leq t \leq 1, \quad k=1, ..., K\] Eqn. 1(a)

\[X_{k}(t)=t\left(\begin{array}{c}{\sin \left[\frac{2 \pi}{K}(2 t+k-1 +\mathcal{N}\left(0, \sigma^{2}\right))\right]} \\ {\cos \left[\frac{2 \pi}{K}(2 t+k-1 +\mathcal{N}\left(0, \sigma^{2}\right))\right]}\end{array}\right)\\0 \leq t \leq 1, \quad k=1, ..., K\] Eqn. 1(b)

Que signifie effectuer une classification ?
Considérons le cas de la régression logistique. Si la régression logistique pour la classification est appliquée à ces données, elle créera un ensemble de plans linéaires (limites de décision) dans le but de séparer les données en classes. Le problème avec cette solution est que dans chaque région, il y a des points appartenant à plusieurs classes. Les branches de la spirale traversent les limites de décision linéaires. Ce n’est pas une très bonne solution !

Comment pouvons-nous résoudre ce problème ?
Nous transformons l’espace d’entrée de telle sorte que les données soient forcées d’être linéairement séparables. Au cours de l’entraînement d’un réseau de neurones à cette fin, les limites de décision apprises essaieront de s’adapter à la distribution des données d’entraînement.

Note : un réseau de neurones est toujours représenté à partir de la base. La première couche est en bas et la dernière en haut. Ceci est dû au fait que, conceptuellement, les données d’entrée sont des caractéristiques de bas niveau pour n’importe quelle tâche que le réseau neuronal tente d’accomplir. Lorsque les données traversent le réseau de bas en haut, chaque couche suivante extrait des caractéristiques de plus haut niveau.

Données d’entraînement

La semaine précédente, nous avons vu qu’un réseau de neurones nouvellement initialisé transforme son entrée de manière arbitraire. Cette transformation, cependant, n’est pas (initialement) déterminante dans l’accomplissement de la tâche en question. Nous explorons comment, à l’aide de données, nous pouvons forcer cette transformation à avoir une signification qui soit pertinente pour la tâche à accomplir. Les données suivantes sont utilisées comme données d’entraînement pour un réseau.

• $\vect{X}$ représente les données d’entrée, une matrice de dimensions $m$ (nombre de points de données d’entraînement) x $n$ (dimensionnalité de chaque point d’entrée). Dans le cas des données indiquées dans les figures 1(a) et 1(b), $n = 2$.

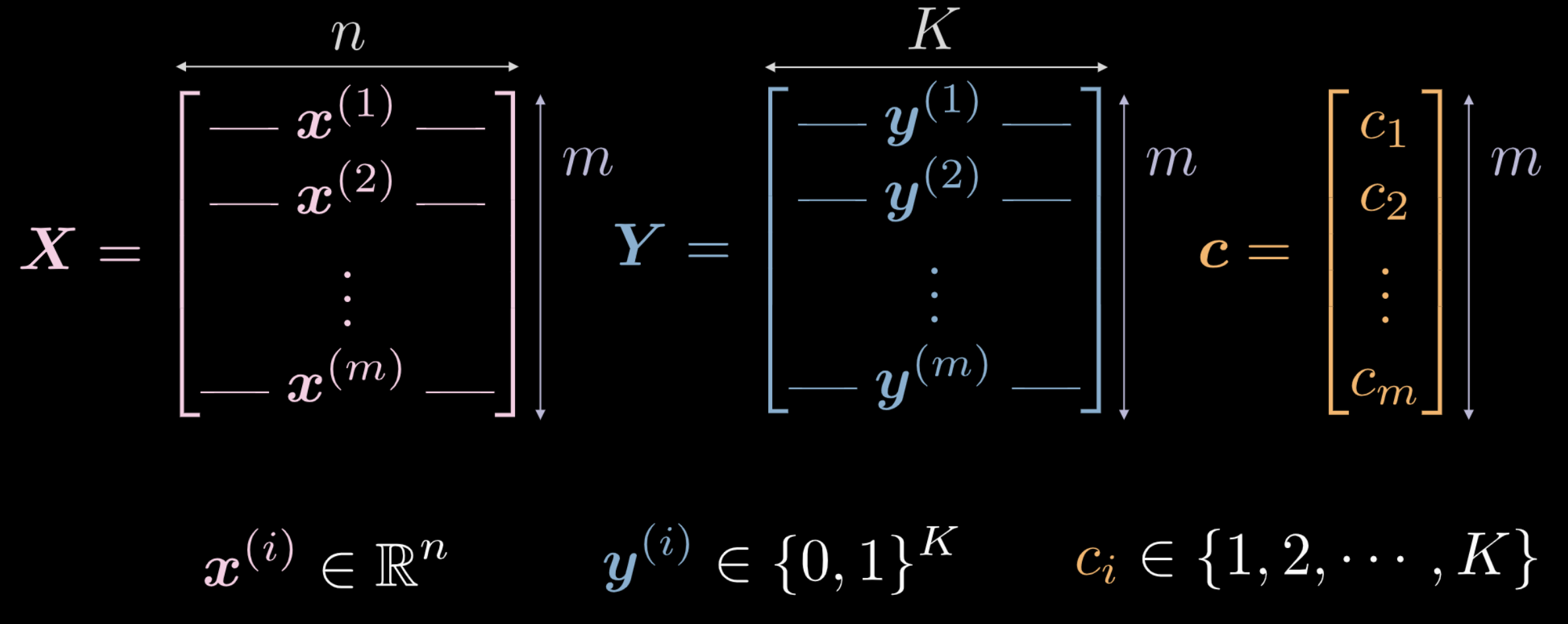
Figure 2 : Données d'entraînement

• Le vecteur $\vect{c}$ et la matrice $\boldsymbol{Y}$ représentent tous deux des labels de classe pour chacun des points de données $m$. Dans l’exemple ci-dessus, il y a $3$ de classes distinctes.

  • $c_i \in \lbrace 1, 2, \cdots, K \rbrace$, et $\vect{c} \in \R^m$. Cependant, nous ne pouvons pas utiliser $\vect{c}$ comme données d’entraînement. Si nous utilisons des labels de classe numériques distinctes $c_i \in \lbrace 1, 2, \cdots, K \rbrace$, le réseau peut déduire un ordre au sein des classes qui n’est pas représentatif de la distribution des données.
  • Pour contourner ce problème, nous utilisons un one-hot encoding. Pour chaque label $c_i$, un vecteur nul de dimension $K$ $\vect{y}^{(i)}$ est créé, dont le $c_i$-ème élément est fixé à $1$ (voir Fig. 3 ci-dessous).

Figure 3 : Un one-hot encoding

• Donc, $\boldsymbol Y \in \R^{m \times K}$. Cette matrice peut également être considérée comme ayant une certaine masse probabiliste, qui est entièrement concentrée sur l’un des points $K$.

Couches entièrement connectées

Nous allons maintenant examiner ce qu’est un réseau entièrement connecté et comment il fonctionne.

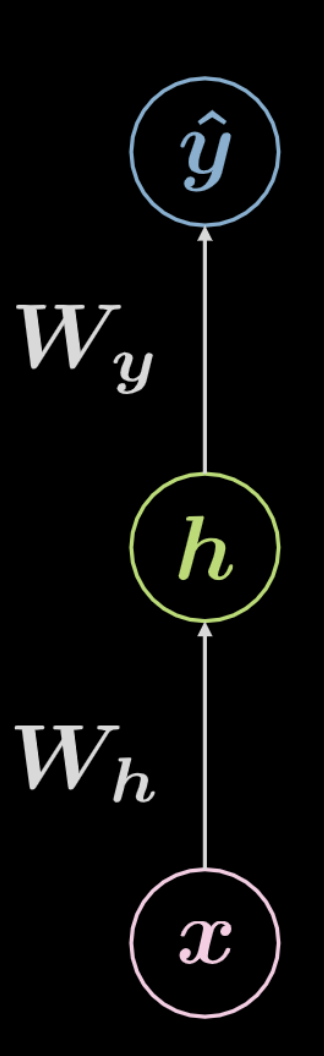
Figure 4 : Réseau neuronal entièrement connecté

Considérons le réseau présenté ci-dessus à la figure 4. Les données d’entrée, $\boldsymbol x$, sont soumises à une transformation affine définie par $\boldsymbol W_h$, suivie d’une transformation non linéaire. Le résultat de cette transformation non linéaire est désigné par $\boldsymbol h$, représentant une sortie cachée, c’est-à-dire qui n’est pas vu de l’extérieur du réseau. Cette transformation est suivie d’une autre transformation affine ($\boldsymbol W_y$), suivie d’une autre transformation non linéaire. Cela produit la sortie finale, $\boldsymbol{\hat{y}}$. Ce réseau peut être représenté mathématiquement par les équations de éqn. 2 ci-dessous. $f$ et $g$ sont tous deux des non-linéarités.

\[\begin{aligned} &\boldsymbol h=f\left(\boldsymbol{W}_{h} \boldsymbol x+ \boldsymbol b_{h}\right)\\ &\boldsymbol{\hat{y}}=g\left(\boldsymbol{W}_{y} \boldsymbol h+ \boldsymbol b_{y}\right) \end{aligned}\] Eqn. 2 : Mathématiques derrière un réseau entièrement connecté

Un réseau neuronal de base tel que celui illustré ci-dessus n’est qu’un ensemble de paires successives. Chaque paire étant une transformation affine suivie d’une opération non linéaire (écrasement). Les fonctions non linéaires les plus fréquemment utilisées sont ReLU, sigmoïde, tangente hyperbolique et softmax.

Le réseau illustré ci-dessus est un réseau à trois couches :

1. neurone d’entrée
2. neurone caché
3. neurone de sortie

Par conséquent, un réseau neuronal à $3$ couches a des transformations affines à $2$. Cela peut être étendu à un réseau à couche $n$.

Passons maintenant à un cas plus complexe.

Faisons un cas de 3 couches cachées, entièrement connectées dans chaque couche. Une illustration peut être trouvée dans la figure 5.

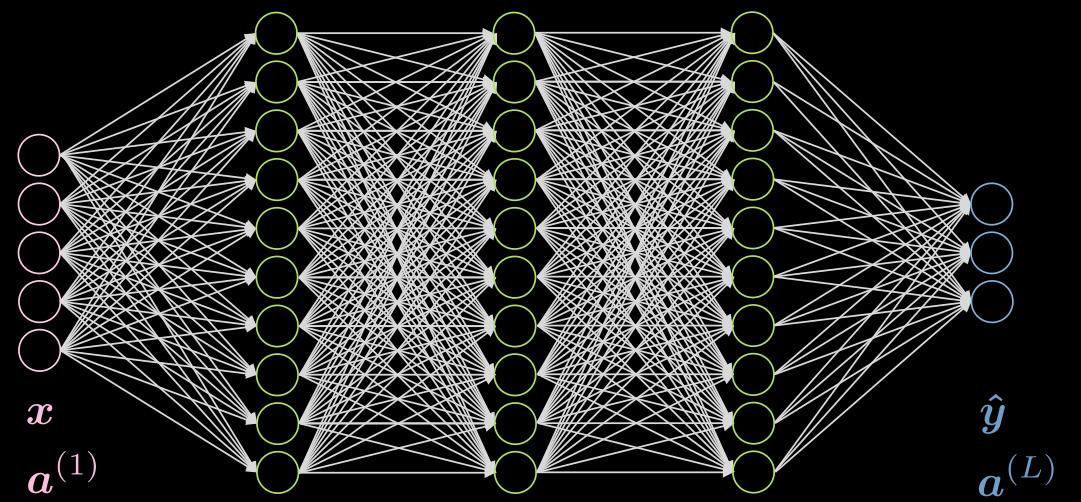
Figure 5 : Réseau neuronal avec 3 couches cachées

Considérons un neurone $j$ dans la deuxième couche. C’est l’activation :

\[a^{(2)}_j = f(\boldsymbol w^{(j)} \boldsymbol x + b_j) = f\Big( \big(\sum_{i=1}^n w_i^{(j)} x_i\big) +b_j ) \Big)\]

où $\vect{w}^{(j)}$ est la $j$-ième ligne de $\vect{W}^{(1)}$.

Dans ce cas, l’activation de la couche d’entrée n’est que l’identité. Les couches cachées peuvent avoir des activations comme ReLU, tangente hyperbolique, sigmoïde, soft(arg)max, etc.

L’activation de la dernière couche en général dépend de votre cas d’utilisation.

Réseau de neurones (inférence)

Pensons encore au réseau neuronal à trois couches (entrée, caché, sortie), comme on le voit sur la figure 6.

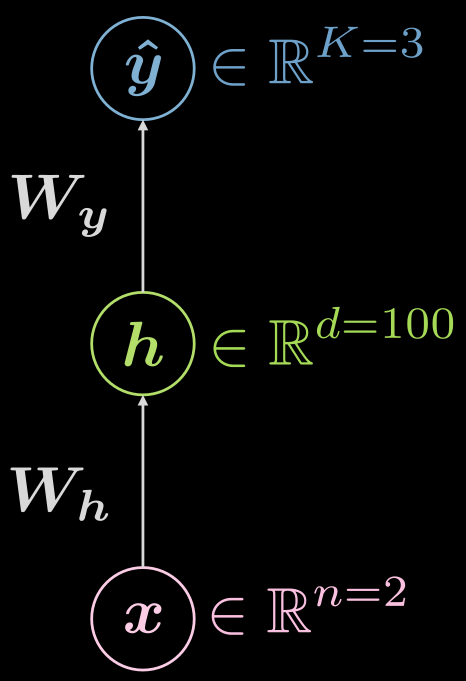
Figure 6 : Réseau neuronal à trois couches

Quel type de fonctions envisageons-nous ?

\[\boldsymbol {\hat{y}} = \boldsymbol{\hat{y}(x)}, \boldsymbol{\hat{y}}: \mathbb{R}^n \rightarrow \mathbb{R}^K, \boldsymbol{x} \mapsto \boldsymbol{\hat{y}}\]

Cependant, il est utile de visualiser le fait qu’il y a une couche cachée et que l’espace où vivent les entités peut être étendu en conséquence :

\[\boldsymbol{\hat{y}}: \mathbb{R}^{n} \rightarrow \mathbb{R}^d \rightarrow \mathbb{R}^K, d \gg n, K\]

À quoi pourrait ressembler un exemple de configuration pour le cas ci-dessus ?
Dans ce cas, on a une entrée de dimension deux ($n=2$), la couche cachée unique pourrait avoir une dimension de $1000$ ($d = 1000$), et nous avons 3 classes ($C=3$). Il y a de bonnes raisons pratiques de ne pas avoir autant de neurones dans une couche cachée, il pourrait donc être logique de diviser cette couche cachée unique en 3 avec 10 neurones chacun ($1000 \rightarrow 10 \times 10 \times 10$).

Réseau de neurones (entraînement I)

À quoi ressemble un entraînement typique ?

Il est utile de formuler cela dans la terminologie standard des pertes. Tout d’abord, réintroduisons la fonction soft(arg)max et précisons explicitement qu’il s’agit d’une fonction d’activation commune pour la dernière couche, lorsque l’on utilise la perte de log-vraisemblance négative, dans les cas de prédiction multiclasses. Comme l’a indiqué Yann lors du cours magistral, c’est parce que vous obtenez de plus jolis gradients que si vous utilisiez les sigmoïdes et la perte quadratique. En outre, votre dernière couche sera déjà normalisée (la somme de tous les neurones de la dernière couche est égale à 1), ce qui est plus intéressant pour les méthodes de gradient que la normalisation explicite (division par la norme).

La fonction soft(arg)max vous donnera des logits dans la dernière couche qui ressemblent à ceci :

\[\text{soft{(arg)}max}(\boldsymbol{l})[c] = \frac{ \exp(\boldsymbol{l}[c])} {\sum^K_{k=1} \exp(\boldsymbol{l}[k])} \in (0, 1)\]

Il est important de noter que l’ensemble n’est pas fermé en raison de la nature strictement positive de la fonction exponentielle.

Étant donné l’ensemble des prédictions $\matr{\hat{Y}}$, la perte sera :

\[\mathcal{L}(\boldsymbol{\hat{Y}}, \boldsymbol{c}) = \frac{1}{m} \sum_{i=1}^m \ell(\boldsymbol{\hat{y}_i}, c_i), \quad \ell(\boldsymbol{\hat{y}}, c) = -\log(\boldsymbol{\hat{y}}[c])\]

Ici, $c$ désigne le label de l’entier, et non la représentation de l’encodage one hot.

Faisons donc deux exemples, un où un exemple est correctement classé, et un autre où il ne l’est pas.

Supposons que

\(\boldsymbol{x}, c = 1 \Rightarrow \boldsymbol{y} = {\footnotesize\begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}}\)

Qu’est-ce que la perte d’instance ?
Dans le cas d’une prévision presque parfaite ($\sim$ signifie circa) :

\[\hat{\boldsymbol{y}}(\boldsymbol{x}) = {\footnotesize\begin{pmatrix} \sim 1 \\\sim 0 \\\\sim 0 \end{pmatrix}} \Rightarrow \ell \left( {\footnotesize\begin{pmatrix} \sim 1 \\\sim 0 \\\\sim 0 \end{pmatrix}} 1\right) \rightarrow 0^{+}\]

Pour le cas presque absolument faux :

\[\hat{\boldsymbol{y}}(\boldsymbol{x}) = {\footnotesize\begin{pmatrix} \sim 0 \\\ \sim 1 \\\ \sim 0 \end{pmatrix}} \Rightarrow \ell \left( {\footnotesize\begin{pmatrix} \sim 0 \\\ \sim 1 \\\ \sim 0 \end{pmatrix}} 1\right) \rightarrow +\infty\]

A noter dans les exemples ci-dessus que $\sim 0 \rightarrow 0^{+}$ et $\sim 1 \rightarrow 1^{-}$.

Note : il est important de savoir que si vous utilisez la CrossEntropyLoss en PyTorch, vous obtiendrez LogSoftMax et NLLLLoss (voir la semaine 11 pour plus de détails sur ces fonctions), alors ne le faites pas deux fois !

Réseau de neurones (entraînement II)

Pour l’entraînement, nous agrégeons tous les paramètres pouvant être entraînés (matrices de poids et biais) dans une collection que nous appelons $\mathbf{\Theta} = \lbrace\boldsymbol{W_h, b_h, W_y, b_y} \rbrace$. Cela nous permet d’écrire la fonction objectif ou la perte comme :

\[J \left( \mathbf{\Theta} \right) = \mathcal{L} \left( \boldsymbol{\hat{Y}}) \left( \mathbf{\Theta} \right), \boldsymbol c \right) \in \mathbb{R}^{+}\]

Cela fait dépendre la perte de la sortie du réseau $\boldsymbol {\hat{Y}} \left( \mathbf{\Theta} \right)$, donc nous pouvons transformer cela en un problème d’optimisation.

Une illustration simple de la façon dont cela fonctionne peut être vue dans la figure 7, où $J(\vartheta)$, la fonction que nous devons minimiser, n’a qu’un paramètre scalaire $\vartheta$.

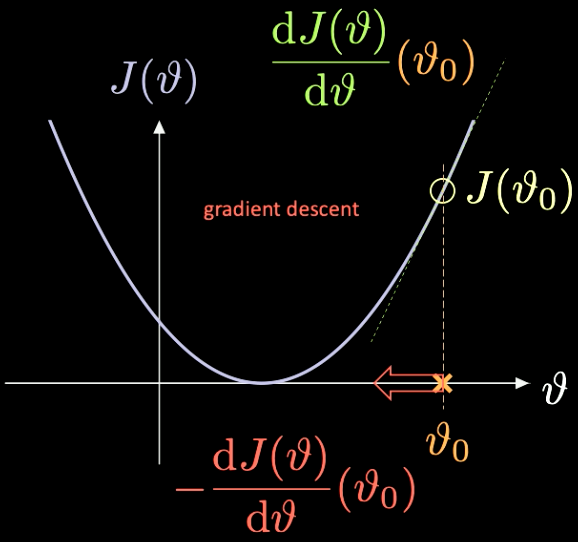
Figure 7 : Optimisation d'une fonction de perte par descente de gradient

Nous choisissons un point d’initialisation aléatoire $\vartheta_0$ avec une perte associée $J(\vartheta_0)$. Nous pouvons calculer la dérivée évaluée à ce point $J’(\vartheta_0) = \frac{\text{d} J(\vartheta)}{\text{d} \vartheta} (\vartheta_0)$. Dans ce cas, la pente de la dérivée est positive. Nous devons donc faire un pas dans la direction de la descente la plus raide. Dans ce cas, c’est $-\frac{\text{d} J(\vartheta)}{\text{d} \vartheta}(\vartheta_0)$.

La répétition itérative de ce processus est connue sous le nom de descente de gradient. Les méthodes de gradient sont les principaux outils pour l’entraînement d’un réseau de neurones.

Afin de calculer les gradients nécessaires, nous devons utiliser la rétropropagation

\[\frac{\partial \, J(\mathbf{\Theta})}{\partial \, \boldsymbol{W_y}} = \frac{\partial \, J(\mathbf{\Theta})}{\partial \, \boldsymbol{\hat{y}}} \; \frac{\partial \, \boldsymbol{\hat{y}}}{\partial \, \boldsymbol{W_y}} \quad \quad \quad \frac{\partial \, J(\mathbf{\Theta})}{\partial \, \boldsymbol{W_h}} = \frac{\partial \, J(\mathbf{\Theta})}{\partial \, \boldsymbol{\hat{y}}} \; \frac{\partial \, \boldsymbol{\hat{y}}}{\partial \, \boldsymbol h} \;\frac{\partial \, \boldsymbol h}{\partial \, \boldsymbol{W_h}}\]

Notebook Jupyter

La version anglaise du notebook Jupyter se trouve ici. La version française se trouve pour sa part ici. Pour le faire fonctionner, assurez-vous que vous avez installé l’environnement pDL comme indiqué dans le fichier README.md. Une explication sur l’utilisation de torch.device() se trouve dans les notes de la semaine 1. Comme auparavant, nous allons travailler avec des points dans $\mathbb{R}^2$ avec trois labels catégoriels différents (en rouge, jaune et bleu ) comme on peut le voir dans figure 8.

Figure 8 : Données de classification en spirale

nn.Sequential() est un conteneur, qui passe les modules au constructeur dans l’ordre où ils sont ajoutés.
nn.linear() est mal nommé car il applique une transformation affine aux données entrantes : $\boldsymbol y = \boldsymbol W \boldsymbol x + \boldsymbol b$. Pour plus d’informations, consultez la documentation PyTorch. N’oubliez pas qu’une transformation affine est composée de cinq choses : rotation, réflexion, translation, mise à l’échelle (la scalabilité) et le shearing.
Comme on peut le voir sur la figure 9, en essayant de séparer les données en spirale avec des limites de décision linéaires (en utilisant uniquement des modules nn.linear(), sans non-linéarité entre eux) le mieux que nous puissions obtenir est une précision de $50\%$.

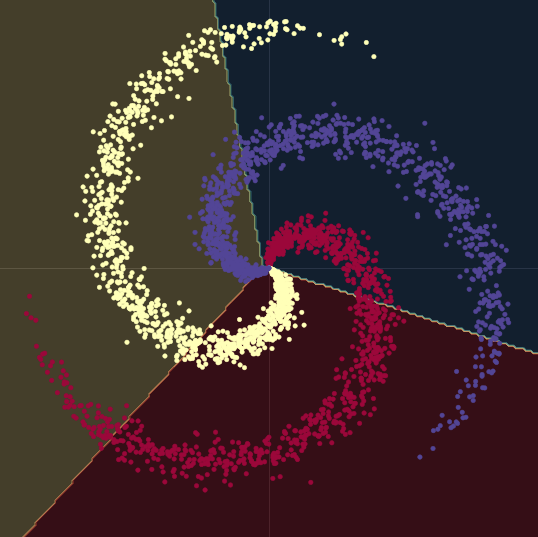
Figure 9 : Limites de décision linéaires

Lorsque nous passons d’un modèle linéaire à un modèle comportant deux modules nn.linear() et un module nn.ReLU() entre eux, la précision passe à 95 %. C’est parce que les limites deviennent non linéaires et s’adaptent beaucoup mieux à la forme en spirale des données, comme on peut le voir sur la figure 10.

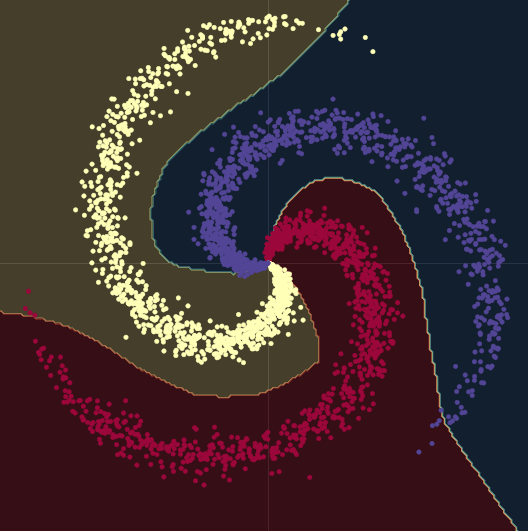
Figure 10 : Limites de décision non linéaires

Un exemple de problème de régression qui ne peut pas être résolu correctement par une régression linéaire, mais qui est facilement résolu avec la même structure de réseau neuronal peut être vu dans ce notebook et dans la figure 11 qui montre 10 réseaux différents, où 5 ont une fonction nn.ReLU() et 5 ont une fonction nn.Tanh(). La première est une fonction linéaire par morceaux, tandis que la seconde est une régression continue et régulière.

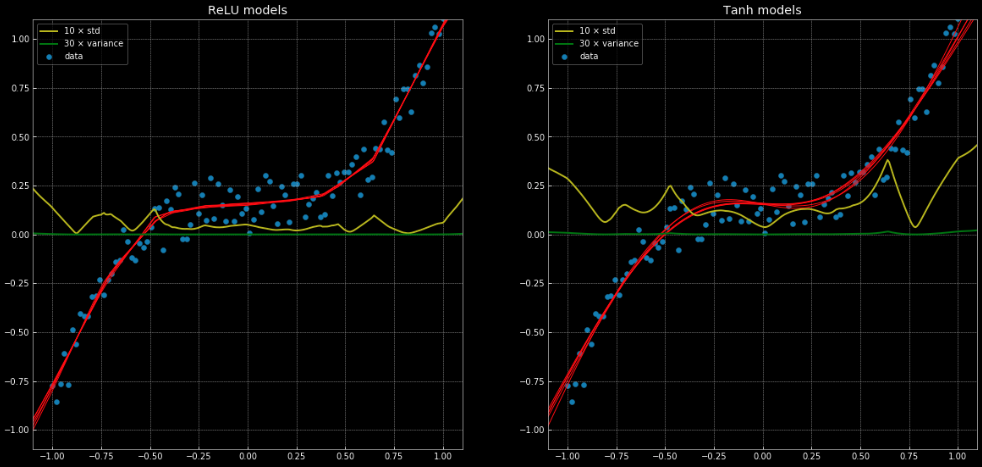
Figure 11 : 10 réseaux de neurones, avec leur variance et leur écart-type.
A gauche : cinq réseaux avec une ReLU. A droite : Cinq réseaux avec une tanh.

Les lignes jaune et verte indiquent l’écart-type et la variance des réseaux. Leur utilisation est utile pour quelque chose de similaire à un intervalle de confiance, puisque les fonctions donnent une seule prédiction par sortie. L’utilisation de la prédiction de la variance d’ensemble nous permet d’estimer l’incertitude avec laquelle la prédiction est faite. L’importance de cette fonction est illustrée par la figure 12 où nous étendons les fonctions de décision en dehors de l’intervalle d’entraînement et où celles-ci tendent vers $+\infty, -\infty$.

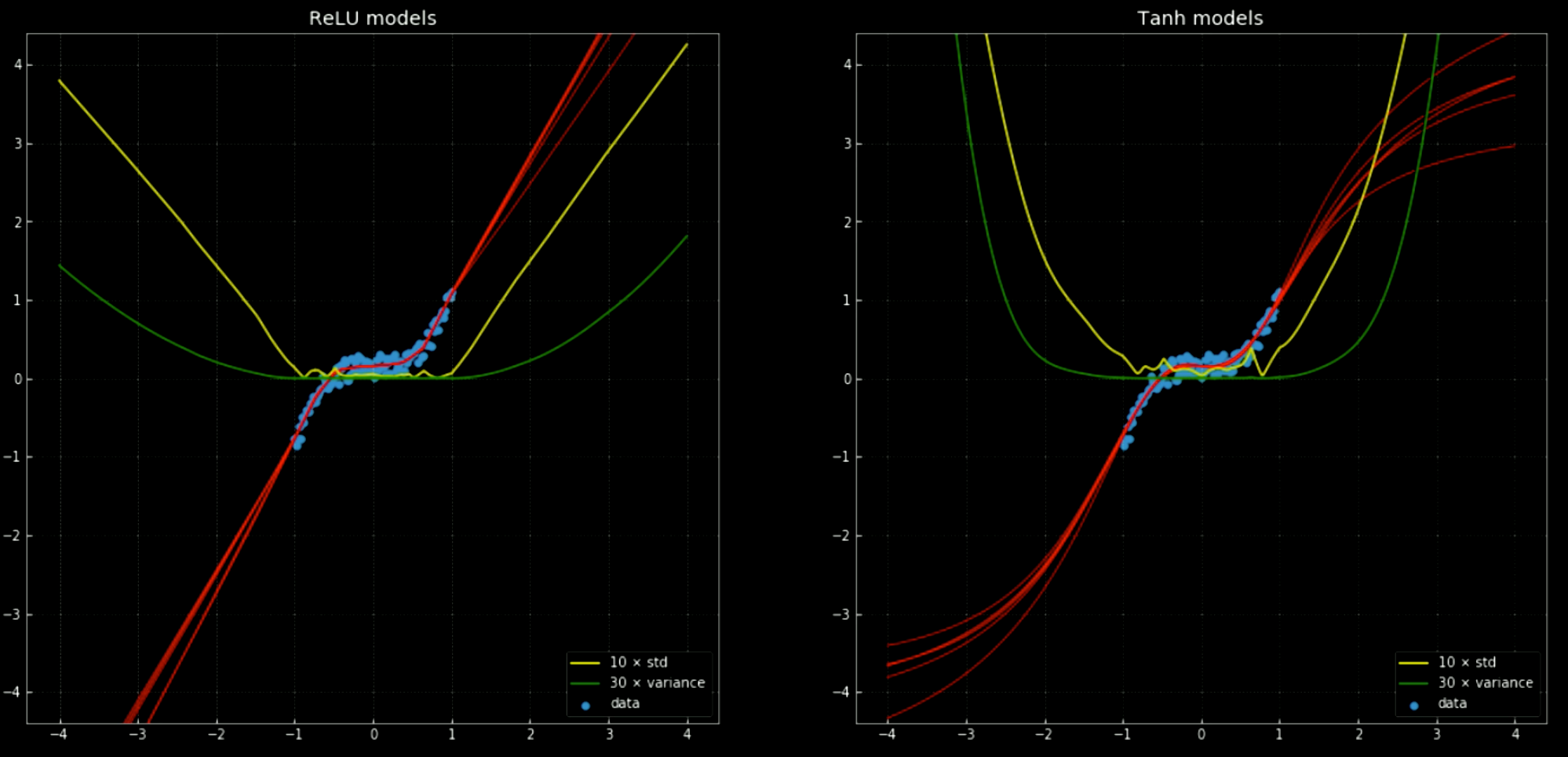
Figure 12 : Réseaux de neurones, avec moyenne et écart-type, en dehors de l'intervalle d'entraînement.
A gauche : cinq réseaux avec une ReLU. A droite : Cinq réseaux avec une tanh.

Pour entraîner un réseau de neurones à l’aide de PyTorch, il faut suivre 5 étapes fondamentales dans la boucle d’entraînement :

1. output = model(input) est la passe en avant du modèle, qui prend l’entrée et génère la sortie.
2. J = loss(output, target <or> label) prend la sortie du modèle et calcule la perte d’entraînement par rapport à la véritable cible.
3. model.zero_grad() nettoie les calculs du gradient afin qu’ils ne soient pas accumulés pour la prochaine passe.
4. J.backward() fait la rétropropagation et l’accumulation. Il calcule $\nabla_\texttt{x} J$ pour chaque variable $\texttt{x}$ pour laquelle nous avons spécifié requires_grad=True. Elles sont cumulées dans le gradient de chaque variable : $\texttt{x.grad} \gets \texttt{x.grad} + \nabla_\texttt{x} J$.
5. optimiser.step() fait un pas dans la descente de la pente : $\vartheta \gets \vartheta - \eta\, \nabla_\vartheta J$.

Lors de l’entraînement d’un réseau, il est très probable que vous ayez besoin de ces 5 étapes dans l’ordre où elles ont été présentées.

---

Loïck Bourdois
4 Feb 2020