Méthodes Contrastives pour les modèles à base d’énergie

Recapitulatif

Comme nous l’avons vu lors du dernier cours, il existe deux grandes catégories de méthodes d’apprentissage :

1. Les méthodes contrastives qui poussent vers le bas l’énergie des points des données d’entraînement, $F(x_i, y_i)$, tout en poussant vers le haut l’énergie sur tous les autres points, $F(x_i, y’)$.
2. Les méthodes architecturales qui construisent une fonction d’énergie $F$ qui minimise/limite les régions à faible énergie en appliquant une régularisation.

Pour distinguer les caractéristiques des différentes méthodes d’entraînement, Yann a listé lors du cours précédent sept stratégies d’entraînement des deux classes mentionnées à l’instant. L’une d’entre elles est une méthode similaire à la méthode du maximum de vraisemblance, qui pousse l’énergie des points de données vers le bas et vers le haut partout ailleurs.

La méthode du maximum de vraisemblance pousse de façon probabiliste les énergies vers le bas des points des données d’entraînement et vers le haut partout ailleurs pour chaque autre valeur de $y’\neq y_i$. La méthode du maximum de vraisemblance ne se soucie pas des valeurs absolues des énergies, mais seulement de la différence entre les énergies. Comme la distribution des probabilités est toujours normalisée à 1, la comparaison du rapport entre deux points donnés est plus utile que la simple comparaison des valeurs absolues.

Méthodes contrastives en apprentissage autosupervisé

Dans les méthodes contrastives, nous poussons vers le bas l’énergie des points des données d’entraînement observés ($x_i$, $y_i$), tout en poussant vers le haut l’énergie des points en dehors de la variété des données d’entraînement.

Dans l’apprentissage autosupervisé, nous utilisons une partie des données d’entrée pour prédire les autres parties. Nous espérons que notre modèle peut produire de bonnes caractéristiques pour la vision par ordinateur qui rivalisent avec celles des tâches supervisées.

Les chercheurs ont constaté empiriquement que l’application de méthodes d’enchâssement contrastives (contrastive embedding methods) à des modèles d’apprentissage autosupervisé peut donner de bonnes performances rivalisant avec celles des modèles supervisés. Nous allons explorer certaines de ces méthodes et leurs résultats.

Méthodes d’enchâssement contrastives

Considérons une paire ($x$, $y$), telle que $x$ est une image et $y$ est une transformation de $x$ qui préserve son contenu (rotation, grossissement, recadrage, etc.). Nous appelons cette paire, une paire positive.

Figure 1 : Paire positive

Conceptuellement, les méthodes d’enchâssement contrastives prennent un réseau convolutif et passent $x$ et $y$ à travers ce réseau pour obtenir deux vecteurs de caractéristiques : $h$ et $h’$. Comme $x$ et $y$ ont le même contenu (une paire positive), nous voulons que leurs vecteurs de caractéristiques soient aussi similaires que possible. Par conséquent, nous choisissons une métrique de similarité (telle que la similarité cosinus) et une fonction de perte qui maximise la similarité entre $h$ et $h’$. Ce faisant, nous réduisons l’énergie des images sur la variété des données d’entraînement.

Figure 2 : Paire négative

Cependant, nous devons également pousser l’énergie des points situés en dehors de cette variété. Ainsi, nous générons également des échantillons négatifs ($x_{\text{neg}}$, $y_{\text{neg}}$), des images au contenu différent (labels de classe différents par exemple). Nous les transmettons à notre réseau, obtenons les vecteurs de caractéristiques $h$ et $h’$, et essayons de minimiser la similarité entre eux.

Cette méthode nous permet de pousser vers le bas l’énergie des paires similaires tout en poussant vers le haut l’énergie des paires dissemblables.

Des résultats récents (sur ImageNet) ont montré que cette méthode peut produire des caractéristiques qui sont bonnes pour la reconnaissance d’objets et qui peuvent rivaliser avec les caractéristiques apprises par des méthodes supervisées.

Résultats des méthodes autosupervisées (MoCo, PIRL, SimCLR)

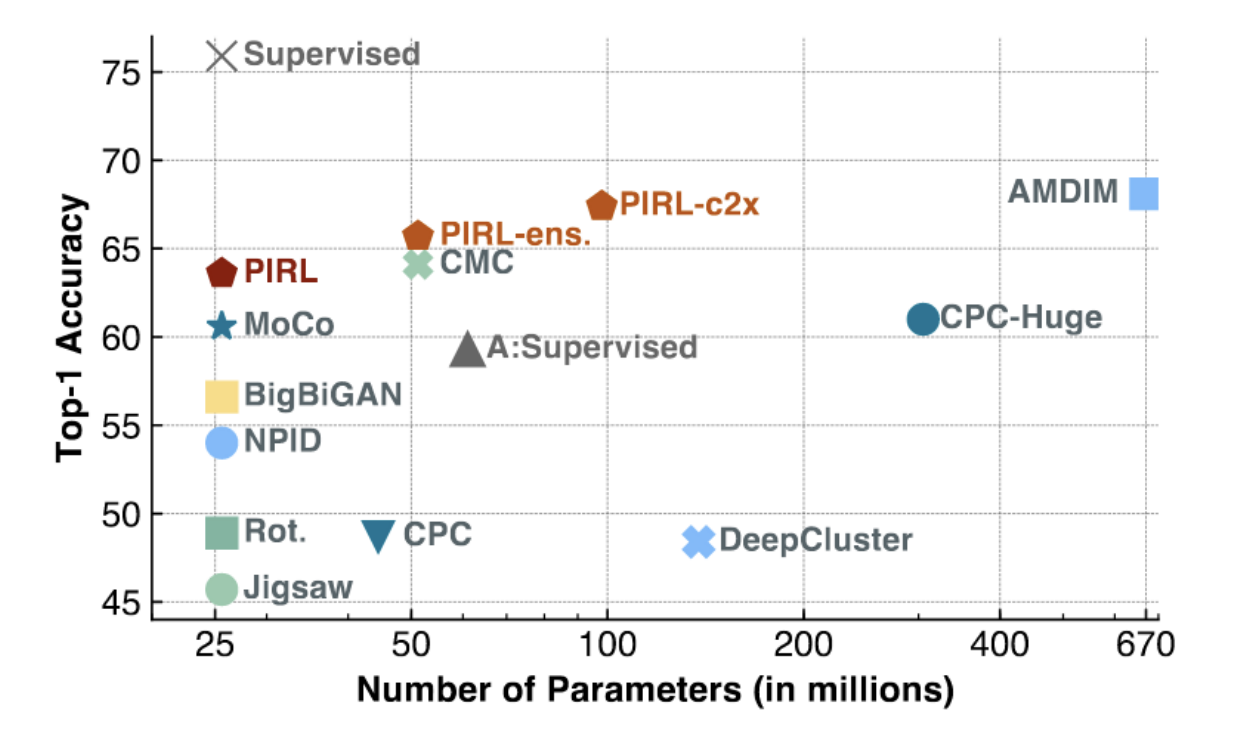
Figure 3 : PIRL et MoCo sur ImageNet

Comme le montre la figure ci-dessus, les méthodes MoCo et PIRL obtiennent les résultats de l’état de l’art (en particulier pour les modèles de faible capacité, avec un petit nombre de paramètres). PIRL commence à se rapprocher du top 1 de la précision linéaire des baselines supervisées (environ 75%).

Nous pouvons mieux comprendre PIRL en examinant sa fonction objectif, la NCE (Noise Contrastive Estimator) :

Nous définissons ici la métrique de similarité entre deux cartes/vecteurs de caractéristiques comme étant la similarité cosinus.

PIRL n’utilise pas la sortie directe de l’extracteur de caractéristiques du ConvNet. Il définit plutôt différentes têtes $f$ et $g$, qui peuvent être considérées comme des couches indépendantes au-dessus de l’extracteur de caractéristiques.

En rassemblant tous ces éléments, la fonction objectif NCE de PIRL fonctionne comme suit.
Dans un mini-batch, nous avons une paire positive (similaire) et de nombreuses paires négatives (dissemblables). Nous calculons ensuite la similarité entre le vecteur caractéristique de l’image transformée ($I^t$) et le reste des vecteurs caractéristiques du mini-batch (un positif, le reste négatif). Nous calculons ensuite le score d’une fonction de type softmax sur la paire positive. Maximiser un score softmax signifie minimiser le reste des scores, ce qui est exactement ce que nous voulons pour un modèle à base d’énergie. La fonction de perte finale nous permet donc de construire un modèle qui pousse l’énergie vers le bas sur des paires similaires tout en la poussant vers le haut sur des paires dissemblables.

Yann mentionne que pour que cela fonctionne, il faut un grand nombre d’échantillons négatifs. Dans la SGD, il peut être difficile de maintenir de façon constante un grand nombre de ces échantillons négatifs à partir de mini-batchs. C’est pourquoi PIRL utilise également une banque mémoire en cache.

Pourquoi utilisons-nous la similarité cosinus au lieu de la norme L2 ?

Avec une norme L2, il est très facile de rendre deux vecteurs similaires en les rendant « courts » (proches du centre) ou de rendre deux vecteurs dissemblables en les rendant très « longs » (éloignés du centre). En effet, la norme L2 n’est qu’une somme des carrés des différences partielles entre les vecteurs. Ainsi, l’utilisation de la similarité cosinus oblige le système à trouver une bonne solution sans « tricher » en rendant les vecteurs courts ou longs.

SimCLR

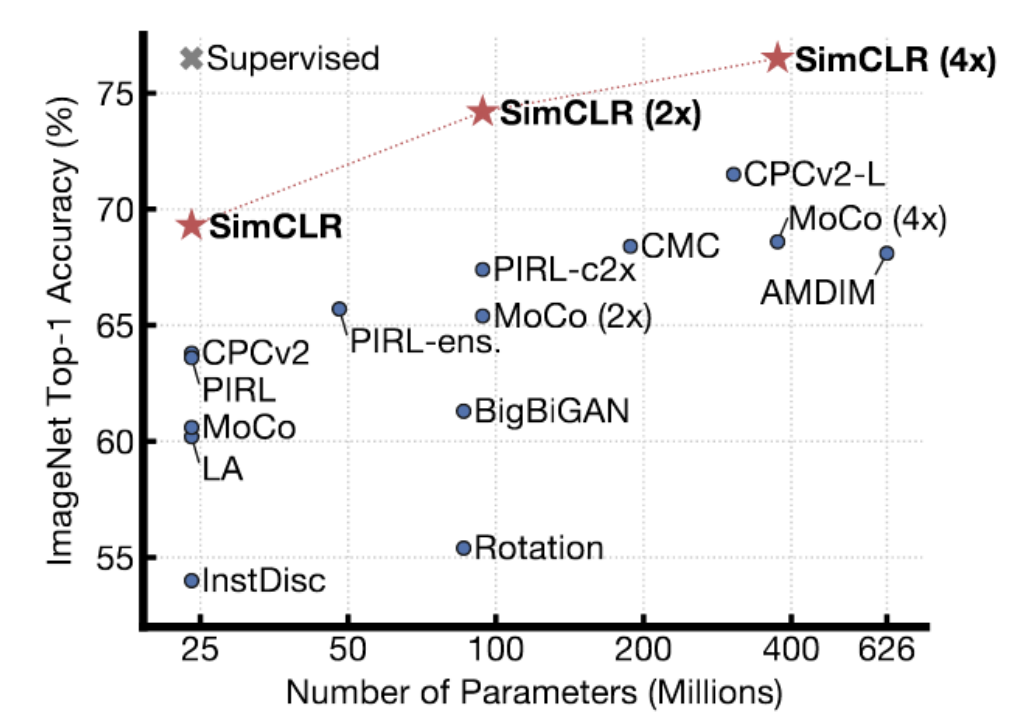
Figure 4 : Résultats de SimCLR sur ImageNet

SimCLR donne de meilleurs résultats que les méthodes précédentes. En fait, avec un nombre de paramètres suffisants, elle atteint les performances des méthodes supervisées de la « top-1 linear accuracy » sur ImageNet. La technique utilise une méthode sophistiquée d’augmentation de données pour générer des paires similaires et l’entraînement est réalisé pendant un temps considérable (avec des batchs très très importants) sur des TPUs. Yann pense que SimCLR, dans une certaine mesure, montre la limite des méthodes contrastives. Il y a beaucoup beaucoup de régions dans un espace en grande dimension où il faut pousser l’énergie vers le haut pour s’assurer qu’elle est effectivement plus élevée que sur la surface de données. Au fur et à mesure que vous augmentez la dimension de la représentation, vous avez besoin de plus en plus d’échantillons négatifs pour vous assurer que l’énergie est plus élevée dans les endroits qui ne sont pas sur la surface.

Auto-encodeur débruiteur

Dans les travaux dirigés de la semaine 7, nous avons discuté de l’auto-encodeur débruiteur. Le modèle tend à apprendre la représentation des données en reconstruisant l’entrée corrompue à l’entrée originale. Plus précisément, nous entraînons le système à produire une fonction d’énergie qui croît quadratiquement à mesure que les données corrompues s’éloignent de la variétés des données.

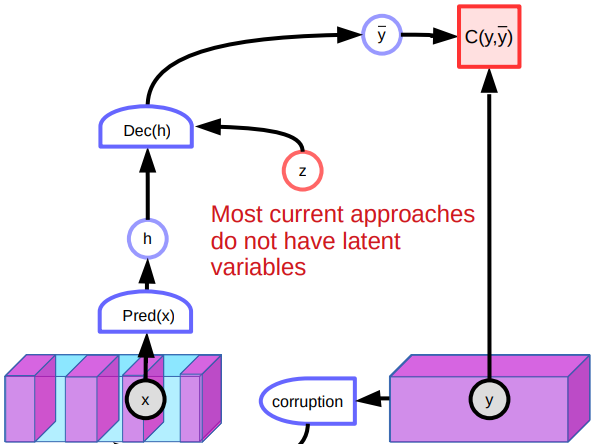
Figure 5 : Architecture de l’auto-encodeur débruiteur

Problèmes

Cependant, l’auto-encodeur débruiteur pose plusieurs problèmes. L’un des problèmes est que dans un espace continu de grande dimension, il existe d’innombrables façons de corrompre une donnée. Il n’y a donc aucune garantie que nous puissions modeler la fonction d’énergie en poussant simplement sur un grand nombre d’endroits différents.
Un autre problème avec le modèle est qu’il est peu performant lorsqu’il s’agit d’images en raison de l’absence de variables latentes. Comme il existe de nombreuses façons de reconstruire les images, le système produit diverses prédictions et n’apprend pas de bonnes caractéristiques. En outre, les points corrompus au milieu de la variété pourraient être reconstruits des deux côtés. Cela créera des points plats dans la fonction d’énergie et affectera la performance globale.

Autres méthodes contrastives

Il existe d’autres méthodes contrastives telles que la divergence contrastive, le Ratio Matching, le Noise Contrastive Estimation ou encore le Minimum Probability Flow. Nous abordons brièvement l’idée de base de la divergence contrastive.

Divergence contrastive

La divergence contrastive est un autre modèle qui apprend la représentation en corrompant intelligemment l’échantillon d’entrée. Dans un espace continu, nous choisissons d’abord un échantillon d’entraînement $y$ et nous en diminuons l’énergie. Pour cet échantillon, nous utilisons une sorte de processus basé sur des gradients pour descendre sur la surface de l’énergie avec du bruit. Si l’espace d’entrée est discret, nous pouvons à la place perturber l’échantillon d’entraînement de manière aléatoire pour modifier l’énergie. Si l’énergie que nous obtenons est plus faible, nous la gardons. Sinon, nous la rejetons avec une certaine probabilité. Si nous continuons ainsi, nous finissons par diminuer l’énergie de $y$. Nous pouvons alors mettre à jour le paramètre de notre fonction d’énergie en comparant $y$ et l’échantillon contrasté $\bar y$ avec une certaine fonction de perte.

Divergence contrastive persistante

L’un des raffinements de la divergence contrastive est la divergence contrastive persistante. Le système utilise un groupe de « particules » et se souvient de leurs positions. Ces particules sont déplacées vers le bas sur la surface d’énergie, tout comme nous l’avons fait dans la divergence contrastive ordinaire. Finalement, elles trouvent des endroits à faible énergie dans notre surface énergétique et les font monter. Cependant, le système ne s’adapte pas bien à l’échelle car la dimensionnalité augmente.