Méthodes graphiques à base d'énergie
🎙️ Yann Le CunComparer les pertes
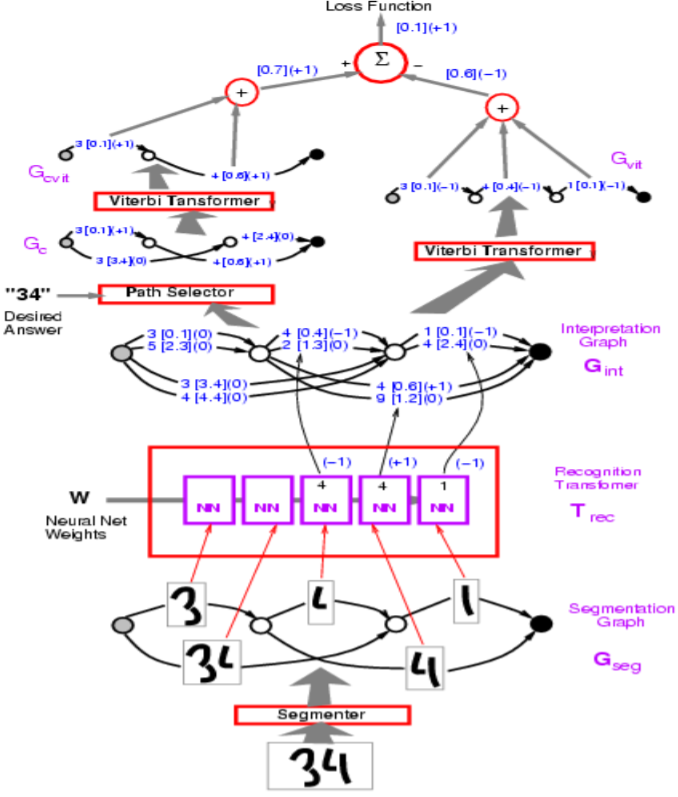
Figure 1 : Architecture de réseau
Dans la figure ci-dessus, les chemins incorrects ont une valeur de $-1$.
Yann commence par la perte de perceptron, qui est utilisée dans l’exemple du Graph Transformer Model dans la figure ci-dessus. L’objectif est de faire en sorte que l’énergie des mauvaises réponses soit grande et celle des bonnes petites.
En termes de mise en œuvre, nous représenterons les arcs dans la visualisation avec un vecteur. Plutôt qu’un arc séparé pour chaque catégorie, un vecteur contient à la fois les catégories et le score de chaque catégorie.
Comment le segmenteur est-il implémenté dans le modèle ci-dessus ?
Le segmenteur est une heuristique artisanale. Le modèle utilise un segment artisanal bien qu’il y ait un moyen de le rendre entraînable de bout en bout. Cette approche artisanale a été remplacée par l’approche de la fenêtre coulissante pour la reconnaissance des caractères.
Aperçu des pertes
| Équation de perte | Formule | Marge |
|---|---|---|
| Perte d’énergie | $\text{E}(\text{W}, \text{Y}^i, \text{X}^i)$ | Aucune |
| Perceptron | $\text{E}(\text{W}, \text{Y}^i, \text{X}^i)-\min\limits_{\text{Y}\in\mathcal{Y}}\text{E}(\text{W}, \text{Y}, \text{X}^i)$ | 0 |
| Hinge | $\max\big(0, m + \text{E}(\text{W}, \text{Y}^i,\text{X}^i)-\text{E}(\text{W}, \overline{\text{Y}}^i,\text{X}^i)\big)$ | $m$ |
| Log | $\log\bigg(1+\exp\big(\text{E}(\text{W}, \text{Y}^i,\text{X}^i)-\text{E}(\text{W}, \overline{\text{Y}}^i,\text{X}^i)\big)\bigg)$ | >0 |
| LVQ2 | $\min\bigg(M, \max\big(0, \text{E}(\text{W}, \text{Y}^i,\text{X}^i)-\text{E}(\text{W}, \overline{\text{Y}}^i,\text{X}^i)\big)\bigg)$ | 0 |
| MCE | $\bigg(1+\exp\Big(-\big(\text{E}(\text{W}, \text{Y}^i,\text{X}^i)-\text{E}(\text{W}, \overline{\text{Y}}^i,\text{X}^i)\big)\Big)\bigg)^{-1}$ | >0 |
| Square-Square | $\text{E}(\text{W}, \text{Y}^i,\text{X}^i)^2-\bigg(\max\big(0, m - \text{E}(\text{W}, \overline{\text{Y}}^i,\text{X}^i)\big)\bigg)^2$ | $m$ |
| Square-Exp | $\text{E}(\text{W}, \text{Y}^i,\text{X}^i)^2 + \beta\exp\big(-\text{E}(\text{W}, \overline{\text{Y}}^i,\text{X}^i)\big)$ | >0 |
| NNL/MMI | $\text{E}(\text{W}, \text{Y}^i,\text{X}^i) + \frac{1}{\beta}\log\int_{y\in\mathcal{Y}}\exp\big(-\beta\text{E}(\text{W}, y,\text{X}^i)\big)$ | >0 |
| MEE | $1-\frac{\exp\big(-\beta E(W,Y^i,X^i)\big)}{\int_{y\in\mathcal{Y}}\exp\big(-\beta E(W,y,X^i)\big)}$ | >0 |
La perte de perceptron observée dans le tableau ci-dessus n’a pas de marge et donc risque de s’effondrer.
La perte de perceptron consiste à calculer la différence d’énergie entre celle de la réponse la plus offensante et celle de la bonne réponse. Intuitivement, avec une marge m, l’hinge aura une perte de $0$ que lorsque l’énergie correcte est inférieure à l’énergie la plus offensante d’au moins m.
La perte MCE est utilisée dans la reconnaissance vocale et ressemble à une sigmoïde.
La perte NLL vise à rendre l’énergie de la bonne réponse petite et la composante logarithmique de l’équation grande.
Comment la perte hinge peut-elle être meilleure que la perte NLL ?
La perte hinge est meilleure que la perte NLL parce que NLL essaie de pousser la différence entre la bonne réponse et les autres réponses à l’infini, alors que l’hinge veut seulement la rendre plus grande qu’une certaine valeur (la marge m).
Définition :
Un décodeur entre une séquence de vecteurs qui indiquent les scores ou l’énergie des différents sons ou images, et choisit la meilleure sortie possible. Il peut être utile pour tout ce qui est modélisation du langage, traduction automatique et marquage des séquences.
Algorithme forward dans les réseaux Graph Transformer Networks
Composition de graphes
La composition de graphes nous permet de combiner deux graphes. Dans cet exemple, nous pouvons voir un lexique de modèle de langage représenté par un $trie$ (un graphe) et un graphe de reconnaissance qui est produit par un réseau de neurones.
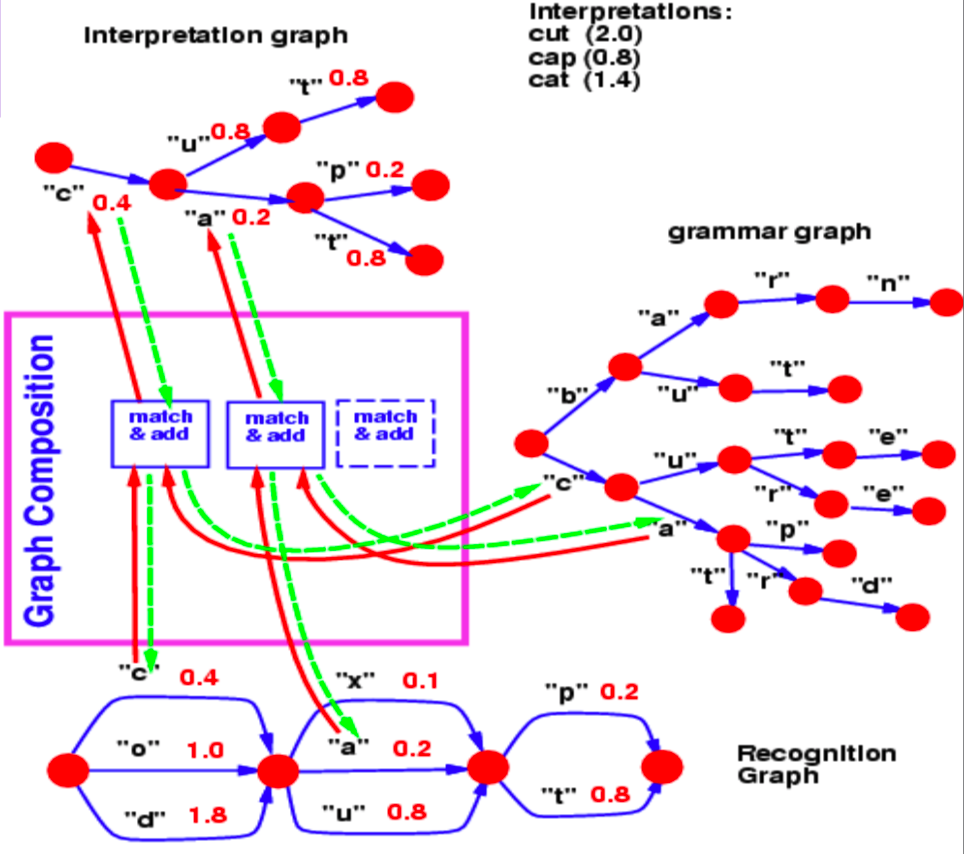
Figure 2 : Composition de graphes
Le graphe de reconnaissance spécifie avec différentes valeurs d’énergie (associées à chaque arc) la probabilité qu’un personnage se trouve à une étape particulière.
Maintenant, pour cet exemple, la question à laquelle nous répondons par une opération de composition de graphes est la suivante : quel est le meilleur chemin dans ce graphe qui est également d’accord avec notre lexique ?
Le saut commun de l’étape 1 à l’étape 2 entre le graphe de reconnaissance et la grammaire est le caractère $c$, associé à l’énergie $0,4$. Ainsi, notre graphe d’interprétation ne contient qu’un seul arc entre les étapes 1 et 2 correspondant à $c$. De même, les caractères possibles entre les étapes 2 et 3 sont $x$, $u$ et $a$ dans le graphe de reconnaissance. Les branches suivant $c$ dans le graphe de grammaire contiennent $u$ et $a$. Ainsi, l’opération de composition de graphes permet de repérer les arcs $u$ et $a$ qui doivent être présents dans le graphe d’interprétation. Elle associe également l’arc qu’elle copie du graphe de reconnaissance à leurs valeurs énergétiques.
Si la grammaire contenait également des valeurs énergétiques associées aux arcs, la composition du graphe aurait ajouté les valeurs d’énergie ou les aurait combinées à l’aide d’un autre opérateur.
De la même manière, la composition des graphes nous permet également de combiner deux bases de connaissances représentées par des réseaux de neurones. Dans l’exemple présenté ci-dessus, la grammaire peut être représentée essentiellement comme un réseau de neurones prédisant le prochain caractère. La sortie softmax du réseau neuronal nous fournit les probabilités de transition vers le caractère suivant à partir d’un nœud donné.
Par ailleurs, si le modèle de langage présenté dans cet exemple est un réseau de neurones, nous pouvons faire une rétropropagation à travers toute la structure. Ceci devient un exemple de programme différenciable où nous faisons une rétropropagation à travers un programme contenant des boucles, des conditions if, des récursions, etc.
Un lecteur de chèques du milieu des années 90
L’ensemble de l’architecture d’un lecteur de chèques du milieu des années 1990 est assez complexe, mais ce qui nous intéresse avant tout, c’est la partie partant du reconnaisseur de caractères produisant le graphe de reconnaissance.
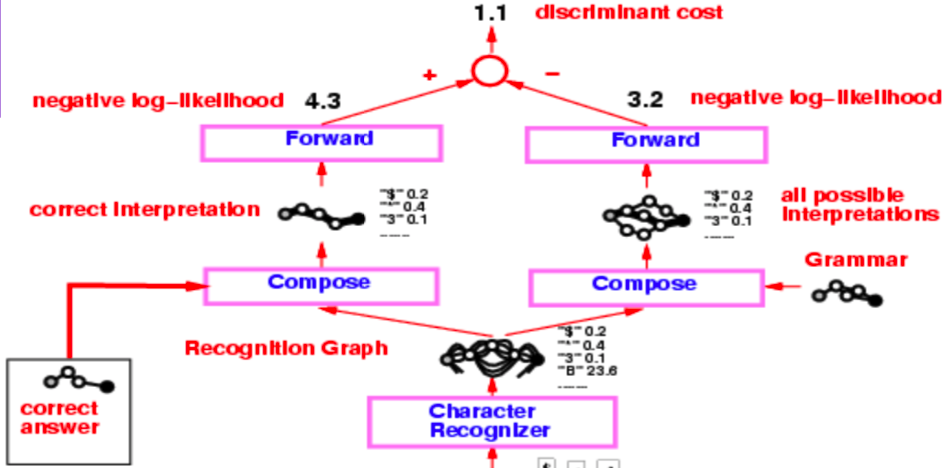
Figure 3 : Lecteur de chèque
Ce graphe de reconnaissance subit deux opérations de composition distinctes, la première avec l’interprétation correcte (ou la vérité de base) et la seconde avec la grammaire qui crée un graphe de toutes les interprétations possibles.
L’ensemble du système est entraîné par la fonction de perte de log-vraisemblance négative. La log-vraisemblance négative indique que chaque chemin dans le graphe d’interprétation est une interprétation possible et que la somme des énergies le long de ce chemin est l’énergie de cette interprétation.
Maintenant, au lieu d’utiliser l’algorithme de Viterbi, nous utilisons l’algorithme forward. Les sous-sections suivantes traitent des différences entre les deux approches.
Algorithme de Viterbi
L’algorithme de Viterbi est un algorithme de programmation dynamique qui est utilisé pour trouver le chemin le plus probable (ou le chemin avec le minimum d’énergie) dans un graphe donné. Il minimise l’énergie par rapport à une variable latente z, où z représente le chemin que nous empruntons dans le graphe.
\[F (x, y) = \min_{z} \ ; E(x, y, z)\]L’algorithme forward
L’algorithme forward, quant à lui, calcule le logarithme de la somme des exponentielles de la valeur négative des énergies de tous les chemins. On peut facilement voir cela sous la forme d’une formule ci-dessous :
\[F_{\beta} (x, y) = -\frac{1}{\beta} \; \log \; \sum_{z \, \in \, \text{paths}} \; \exp \, (- \beta \; E(x, y, z))\]Cela marginalise par rapport à la variable latente $z$ qui définit les chemins dans un graphe d’interprétation. Cette approche calcule la valeur exponentielle de cette somme logarithmique sur tous les chemins possibles vers un nœud particulier. C’est comme si l’on combinait le coût de tous les chemins possibles d’une manière douce et minimale.
L’algorithme forward est peu coûteux à mettre en œuvre et ne coûte pas plus cher que l’algorithme de Viterbi. De plus, nous pouvons faire une rétropropagation à travers le nœud de l’algorithme foward dans le graphe.
Le fonctionnement de l’algorithme foward peut être montré à l’aide de l’exemple suivant défini sur un graphe d’interprétation.
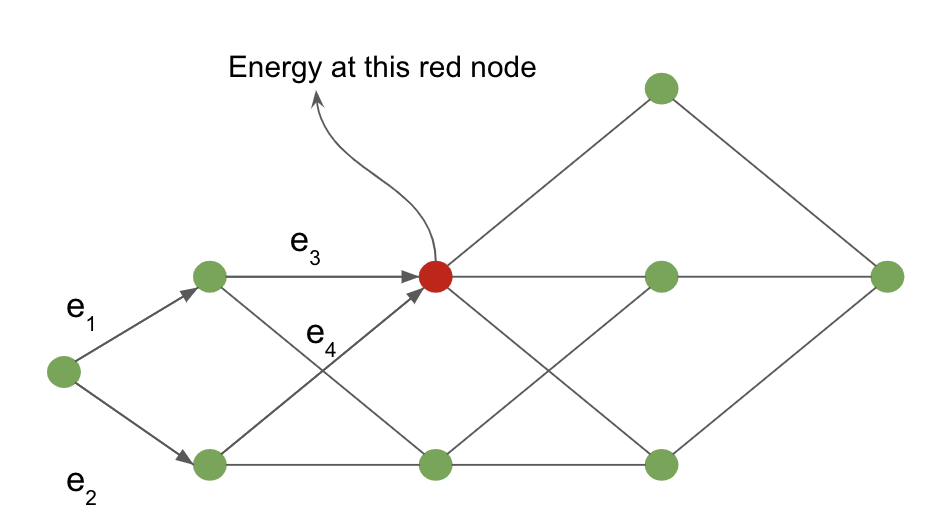
Figure 4 : Graphe d'interprétation
Le coût du nœud d’entrée au nœud rouge est calculé en marginalisant sur tous les chemins possibles atteignant le nœud rouge. Les flèches qui entrent dans le nœud rouge définissent ces chemins possibles dans notre exemple.
Pour le nœud rouge, la valeur de l’énergie au nœud est donnée par :
\[-\frac{1}{\beta} \; \log \; [ \, \exp \, (- \, \beta (e_1 \, + \, e_3)) \; + \; \exp \, (- \, \beta (e_2 \, + \, e_4)) \, ]\]Analogie du réseau neuronal avec l’algorithme forward
L’algorithme forward est un cas particulier de l’algorithme de propagation des croyances lorsque le graphe sous-jacent est un graphe en chaîne. L’ensemble de l’algorithme peut être considéré comme un réseau neuronal feed-forward où la fonction à chaque nœud est le logarithmique de la somme des exponentielles et un terme d’addition.
Pour chaque nœud du graphe d’interprétation, nous conservons une variable $\alpha$.
\[\alpha_{i} = - \ ; \log \ ; \biggl[ \sum_{k \, \in \, \text{parent} \, (i)} \ ; \exp \, (- \, \beta \ ; (\alpha_k \, + \, e_{ki})) \biggl]\]où $e_{ki}$ est l’énergie du lien entre le nœud $k$ et le nœud $i$.
$\alpha_i$ forme l’activation d’un nœud $i$ dans ce réseau de neurones et $e_{ki}$ est le poids entre les nœuds $k$ et le nœud $i$. Cette formulation est algébriquement équivalente aux opérations de somme pondérée d’un réseau neuronal dans le domaine logarithmique.
Nous pouvons effectuer une rétropropagation à travers le graphe d’interprétation dynamique (puisqu’il change d’un exemple à l’autre) sur lequel nous appliquons l’algorithme forward. Nous pouvons calculer les gradients de $F(x, y)$ calculés au dernier nœud du graphe avec les poids $e_{ki}$ définissant les bords du graphe d’interprétation.

Figure 5 : Lecteur de chèque
Pour revenir à l’exemple du lecteur de chèque, nous appliquons l’algorithme forward sur les deux compositions de graphes et obtenons la valeur énergétique au dernier nœud en utilisant la formule du log de la somme d’exponentielles. La différence entre ces valeurs énergétiques est la perte de log-vraisemblance négative.
La valeur obtenue en appliquant l’algorithme forward sur la composition des graphes entre la bonne réponse et le graphe de reconnaissance est la valeur du logarithme de la somme des exponentielles de la bonne réponse. En revanche, la valeur du logarithme de la somme des exponentielles au dernier nœud de la composition des graphes entre le graphe de reconnaissance et la grammaire est la valeur marginale de toutes les interprétations valides possibles.
Formulation lagrangienne de la rétropropagation
Pour une entrée $x$ et une sortie cible $y$, nous pouvons formuler un réseau comme un ensemble de fonctions $f_k$ et de poids $w_k$ de sorte que les étapes successives du réseau produisent $z_k$ avec $z_{k+1} = f_k(z_k, w_k)$. Dans un environnement supervisé, l’objectif du réseau est de minimiser $C(z_n, y)$, le coût de la sortie $n^\mathrm{th}$ du réseau, par rapport à la vérité de terrain. Ceci est équivalent au problème de la minimisation de $C(z_n, y)$ par rapport aux contraintes $z_{k+1} = f_k(z_k, w_k)$ et $z_0 = x$.
Le Lagrangien peut être écrit comme :
\[\mathcal{L}(x, y, \lambda_i, z_i, w_i) = C(z_n, y) + \sum\limits_{k=0}^{n-1} \lambda^T_{k+1}(z_{k+1} - f_k(z_k, w_k))\]où les termes $ \lambda $ désignent les multiplicateurs de Lagrange (voir ce site (en anglais) pour un rafraîchissement si besoin).
Pour minimiser $\mathcal{L}$, nous devons mettre à zéro les dérivées partielles de $\mathcal{L}$ par rapport à chacun de ses arguments et les résoudre.
- Pour $\lambda$, nous récupérons simplement la contrainte : $\frac{\partial{\mathcal{L}}}{\partial \lambda_{k+1}} = 0 \rightarrow z_{k+1} = f_k(z_k, w_k)$.
- Pour $z_k$, $\frac{\partial \mathcal{L}}{\partial z_k} = 0 \rightarrow \lambda^T_k - \lambda^T_{k+1} \frac{\partial f_k(z_k, w)}{\partial z_k} \rightarrow \lambda_k = \frac{\partial f_k(z_k, w_k)^T}{\partial z_k}\lambda_{k+1}$, qui est juste la formule standard de rétropropagation.
Cette approche est née avec Lagrange et Hamilton dans le contexte de la mécanique classique, où la minimisation est supérieure à l’énergie du système et où les termes $\lambda$ désignent les contraintes physiques du système. Par exemple deux boules qui sont forcées de rester à une distance fixe l’une de l’autre car sont attachées par une barre métallique.
Dans une situation où nous devons minimiser le coût $C$ à chaque pas de temps, $k$, le Lagrangien devient : \(\mathcal{L} = \sum_k \left(C_k(z_k, y_k) + \lambda^T_{k+1}(z_{k+1} - f_k(z_k, w_k)) \right)\).
Equation différentielle ordinaire (ODE) neuronale
En utilisant cette formulation de la rétropropagation, nous pouvons maintenant parler d’une nouvelle classe de modèles : les ODEs neuronales. Il s’agit essentiellement de réseaux récurrents où l’état, $z$, au moment $t$ est donné par : $ z_{t+\text{d}t} = z_t + f(z_t, W) dt $, où $ W$ représente un ensemble de paramètres fixes. Cela peut également être exprimé sous la forme d’une équation différentielle ordinaire (sans dérivée partielle) : $\frac{\text{d}z}{\text{d}t} = f(z_t, W)$.
Entraîner un tel réseau en utilisant la formulation lagrangienne est très simple. Si nous voulons que l’état du système atteigne $y$ dans le temps $T$, nous établissons simplement la fonction de coût comme étant la distance entre $z_T$ et $y$. Un autre objectif du réseau pourrait être de trouver un état stable du système, c’est-à-dire un état qui cesse de changer après un certain point. Mathématiquement, cela équivaut à fixer $\frac{\text{d}z}{\text{d}t} = f(y, W) = 0$. En général, trouver une solution $y$ à cette équation est beaucoup plus facile que la propagation dans le temps car le réseau n’a pas besoin de se souvenir du gradient par rapport à l’ensemble de la séquence. Il doit seulement minimiser $f$ ou $\lvert f \rvert^2$. Pour plus d’informations sur l’entraînement des ODEs neuronales pour atteindre des points fixes, voir Le Cun (1988).
Inférence variationnelle en termes d’énergie
Introduction
Pour une fonction d’énergie élémentaire $E(x,y,z)$, si nous voulons marginaliser sur une variable $z$ pour obtenir une perte en termes de seulement $x$ et $y$, $L(x,y)$, nous devons calculer :
\[L(x,y) = -\frac{1}{\beta}\int_z \exp(-\beta E(x,y,z))\]Si nous multiplions ensuite par $\frac{q(z)}{q(z)}$, nous obtenons : \(L(x,y) = -\frac{1}{\beta}\int_z q(z) \frac{\exp({-\beta E(x,y,z)})}{q(z)}\)
Si nous supposons que $q(z)$ est une distribution de probabilité supérieure à $z$, nous pouvons interpréter notre intégrale de la fonction de perte réécrite comme une valeur attendue, par rapport à la distribution de $\frac{\exp({-\beta E(x,y,z)})}{q(z)}$.
Nous utilisons cette interprétation, l’inégalité de Jensen et des approximations basées sur l’échantillonnage pour optimiser indirectement notre fonction de perte.
L’inégalité de Jensen
L’inégalité de Jensen indique que si nous avons une fonction convexe alors l’espérance de cette fonction sur un intervalle est inférieure à la moyenne de la fonction évaluée au début et à la fin de l’intervalle. Illustrée géométriquement, cette observation est très intuitive :
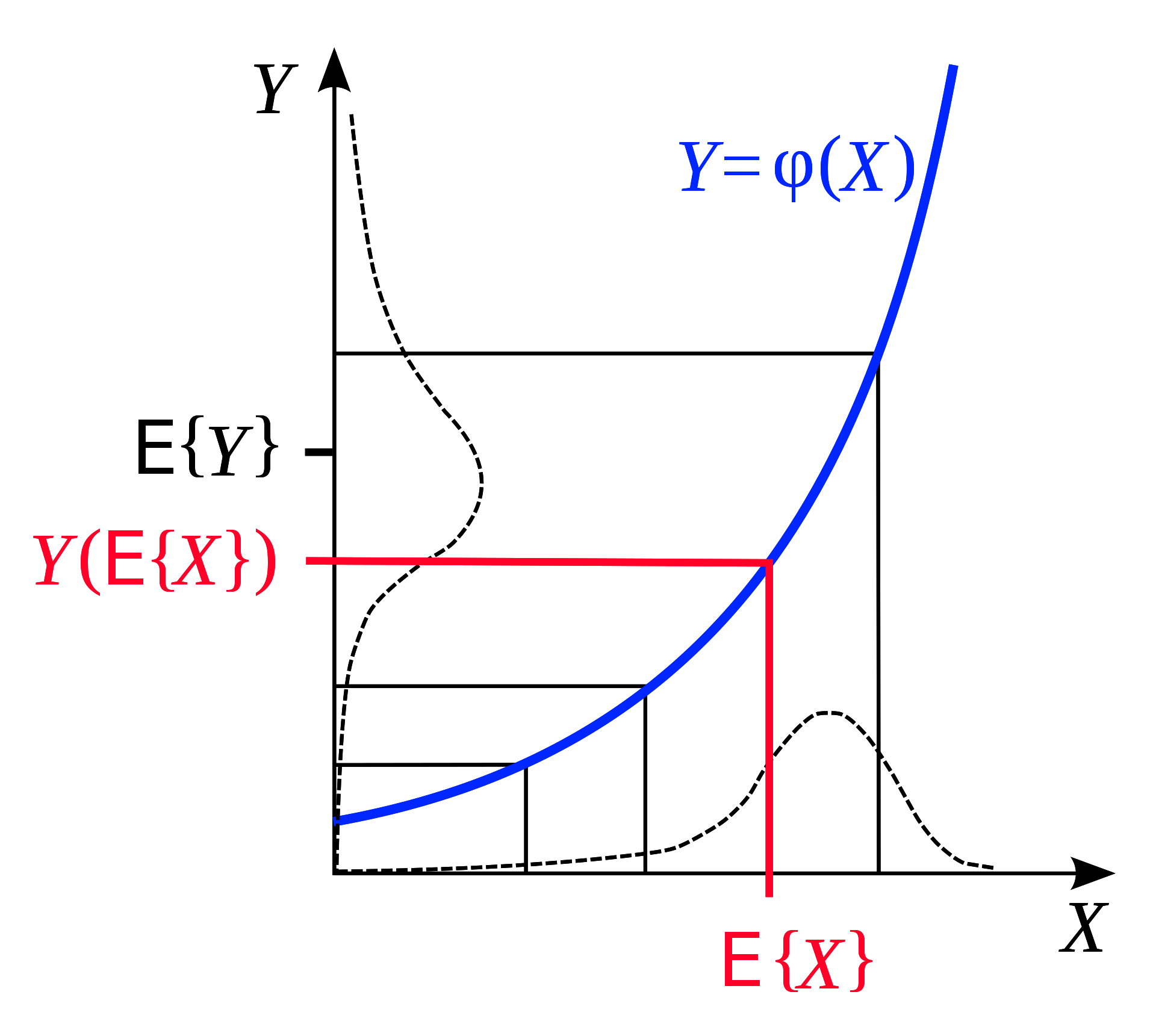
Figure 6 : L'inégalité de Jensen
De même, si $F$ est convexe pour une distribution de probabilité fixe $q$, nous pouvons déduire de l’inégalité de Jensen que sur l’intervalle $z$ :
\[F\Bigg(\int_z q(z)h(z)\Bigg) \leq \int_z q(z)F(h(z)) \tag{1}\]Maintenant, rappelons que notre $L(x,y)$ marginalisée après multiplication avec $\frac{q(z)}{q(z)}$ est :
\(L(x,y) = -\frac{1}{\beta}\int_z q(z) \frac{\exp({-\beta E(x,y,z)})}{q(z)}\)
Si nous faisons $h(z) = -\frac{1}{\beta} \frac{\exp({-\beta E(x,y,z)})}{q(z)}$, nous savons grâce à l’inégalité de Jensen $(1)$ que :
\(F\Bigg(\int_z q(z)\frac{\exp({-\beta E(x,y,z)})}{q(z)}\Bigg) \leq \int_z q(z)F\Bigg(\frac{\exp({-\beta E(x,y,z)})}{q(z)}\Bigg)\) :
Avec une fonction de perte convexe concrète $F(x) = -\log(x)$ :
\[-\log\Bigg(-\frac{1}{\beta}\int_z q(z)\frac{\exp({-\beta E(x,y,z)})}{q(z)}\Bigg) \leq \int_z q(z) * \frac{-1}{\beta}\log\Bigg(\frac{\exp({-\beta E(x,y,z)})}{q(z)}\Bigg)\] \[\leq \int_z q(z)[E(x,y,z) + \frac{1}{\beta}\log(q(z))]\] \[\leq \int_z q(z)E(x,y,z) + \frac{1}{\beta}\int_z q(z)\log(q(z))\]Nous avons maintenant une limite supérieure à notre fonction de perte $L(x,y)$ composée de deux termes que nous comprenons. Le premier terme $\int_z q(z)E(x,y,z)$ est l’énergie moyenne. Le second terme $\frac{1}{\beta}\int_z\log(q(z))$ est juste un facteur ($-\frac{1}{\beta}$) multiplié par l’entropie de la distribution $q$.
Quel est l’intérêt ?
Nous avons maintenant formulé une limite supérieure de manière à éviter les intégrations compliquées, et à la place, nous approximons simplement ces valeurs par un échantillonnage à partir d’une distribution de substitution ($q(z)$), de notre choix !
Pour obtenir la valeur du premier terme de notre fonction de limite supérieure, nous échantillonnons simplement à partir de cette distribution et calculons la valeur moyenne de $L$ que nous obtenons en appliquant nos $z$ échantillonnés.
Le second terme (un facteur d’entropie) est juste une propriété de la famille de distribution et peut également être approximé avec un échantillonnage aléatoire de $q$.
Enfin, nous pouvons minimiser $L$ par rapport à ses paramètres (par exemple, les poids d’un réseau $W$), en minimisant cette fonction qui délimite $L$ ci-dessus. Nous effectuons cette minimisation en mettant à jour nos deux variables : (1) l’entropie de $q$ et (2) les paramètres de notre modèle $W$.
Résumé
Ceci est la vue énergétique de l’inférence variationnelle. Si nous devons calculer le logarithme d’une somme d’exponentielles, remplaçons-le par la moyenne de votre fonction plus un terme d’entropie. Cela nous donne une limite supérieure. Nous minimisons ensuite cette limite supérieure et, ce faisant, nous minimisons la fonction qui nous intéresse réellement.
📝 Yada Pruksachatkun, Ananya Harsh Jha, Joseph Morag, Dan Jefferys-White, and Brian Kelly
Loïck Bourdois
4 May 2020