Inférence pour les modèles à base d’énergie à variable latente

Données d’entraînement et définition du modèle

Pour comprendre pourquoi et comment utiliser un modèle à base d’énergie (EBM), et quel est le format de données qui est pertinent pour ce type de modèle, considérons des échantillons d’entraînement à partir d’une ellipse. La fonction est donnée ci-dessous :

où $x \sim \mathcal{U}(0,1),\space \theta \sim \mathcal{U}(0,2\pi),\space \epsilon \sim \mathcal{N}[0, (\frac{1}{20})^2]$ et $\rho : \mathbb{R} \mapsto \mathbb{R}^2$ associe $x$ à \(\begin{bmatrix}\alpha x + \beta (1-x) \\ \beta x + \alpha (1-x) \end{bmatrix}\exp(2x)\).

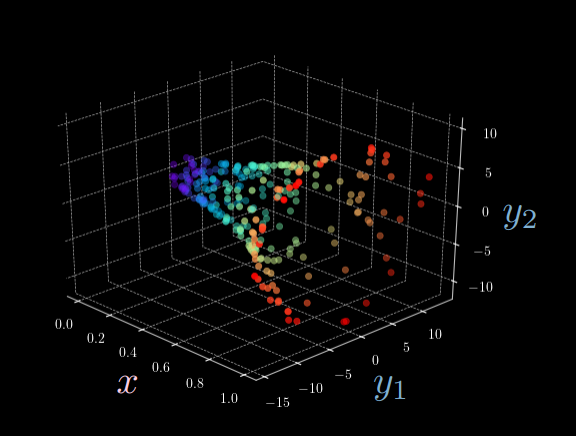
Figure 1 : Visualisation 3D de la fonction de l’ellipse

La figure 1 montre clairement qu’avec une seule entrée $x$, il y a plusieurs sorties possibles $\vect{y}$. En d’autres termes, nous ne pouvons pas identifier une association un à un des vecteurs comme nous l’avions prévu pour les réseaux neuronaux de type feed forward (par exemple, étant donné l’entrée $x$, pour un $y_1$ fixé, il y a presque toujours deux $y_2$ possibles). C’est ici que nous introduisons les modèles à base d’énergie à variable latente.

Pour simplifier, nous fixons l’entrée $x = 0$ et nous laissons $\alpha = 1,5, \beta = 2$, induisant \(\vect{y} = \begin{bmatrix} 2\cos(\theta) + \epsilon \\ 1.5\sin(\theta) + \epsilon \end{bmatrix}\), à partir de laquelle nous échantillonnons aléatoirement 24 points de données $Y = [\vect{y}^{(1)},\ldots,\vect{y}^{(24)}]$. Entre-temps, nous prenons la variable latente $z = [0:\frac{\pi}{24}:2\pi]$ et l’introduisons dans un décodeur pour produire $\tilde{\vect{y}}$ (figures 2 et 3). Ensuite, la fonction d’énergie est calculée comme le carré de la distance euclidienne entre $\vect{y}$ et $\tilde{\vect{y}}$ :

où $\vect{g} = [g_1 \space\space g_2]^{\top} : \mathbb{R} \mapsto \mathbb{R}^2$ et $\vect{g}(z) = \ [w_1 \cos(z) \space\space w_2 \sin(z)]^{\top}$.

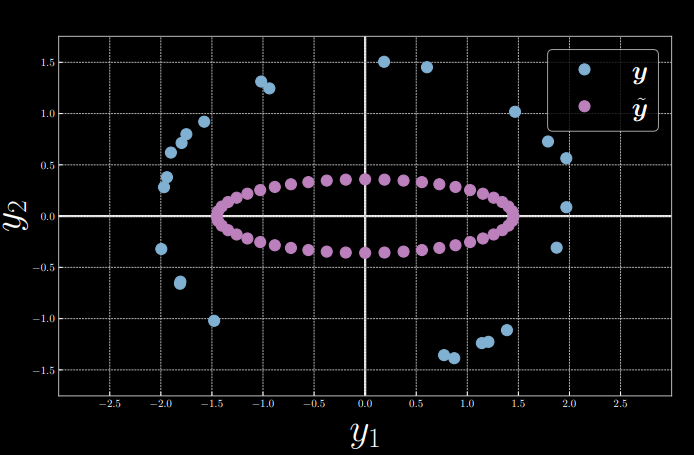
Figure 2 : Exemple de visualisation

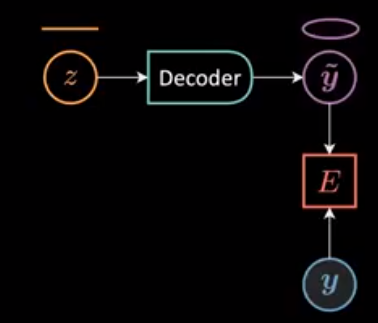
Figure 3 : Graphe du calcul de l'énergie

Pour chaque $\vect{y}^{(i)} \in Y, i \in [1,24]$, nous pouvons calculer l’énergie correspondante donnée à chaque $\tilde{\vect{y}}$ en changeant $z$. Par conséquent, nous pouvons visualiser 24 fonctions d’énergie $E_{1},\ldots,E_{24}$, où la quantité d’énergie sur l’axe des y est tracée en fonction du choix de la variable latente $z$ sur l’axe des $x$ (figure 4).

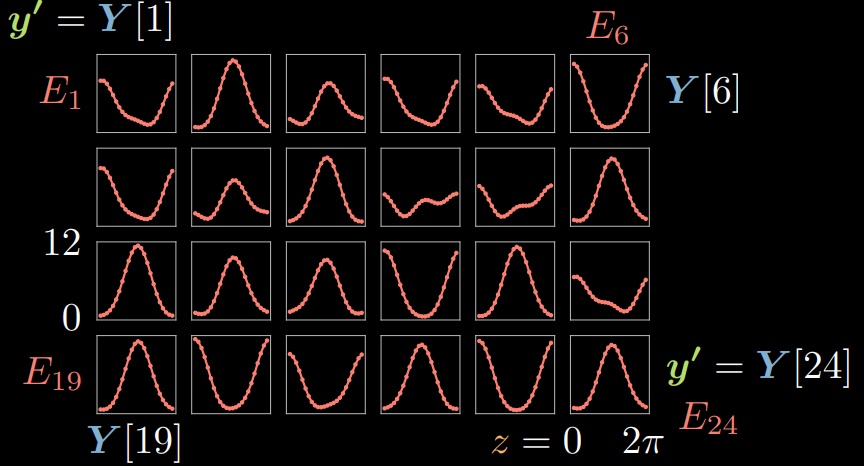
Figure 4 : Fonctions d’énergie sur les échantillons

Energie et énergie libre pour deux exemples d’entraînement

Plongeons dans la forme fonctionnelle des $E(\vect{y}, z)$ pour un $\vect{y}^{(i)}$ donné. La figure 5 montre un tracé de $E(\vect{y}^{(23)}, z) = E_{23}$.

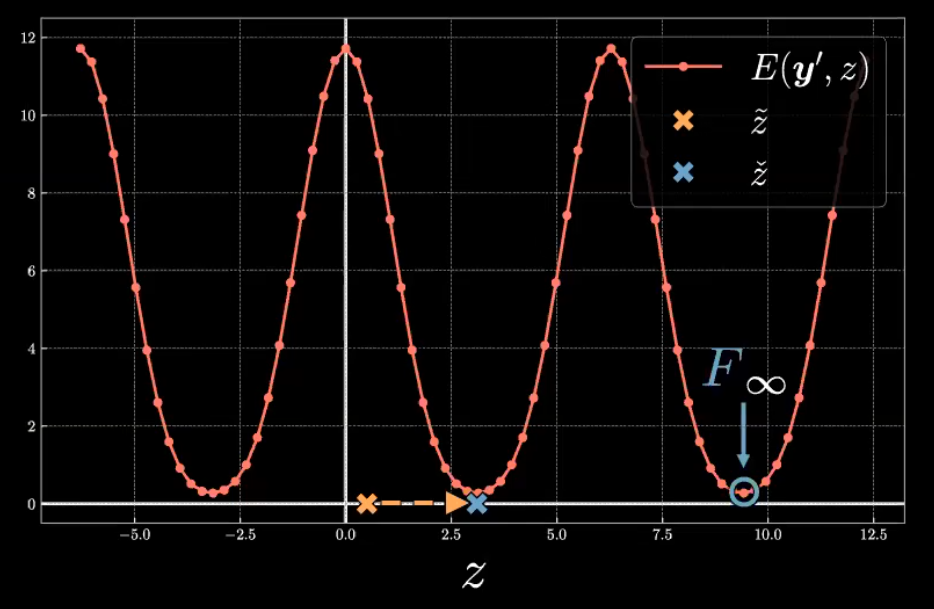
Figure 5 : Fonction d’énergie associée au 23ème échantillon

L’énergie, $E_{23}$, donne une fonction périodique avec un maximum proche de $z=0$ et $2{\pi}$ et un minimum proche de $z={\pi}$. Cette forme symétrique est due à la position $\vect{y}^{(23)}$ dans l’espace $\vect{y}$ par rapport au $\tilde{\vect{y}}$ décodé.

Comme le montre la figure 6, $\vect{y}^{(23)}$ marqué par le point vert, est étroitement aligné sur l’axe horizontal de $\tilde{\vect{y}}$, indiqué en violet. Cela donne une symétrie en $E_{23}$. La variable latente $z$ agit comme un angle de coordonnées polaires inversées de telle sorte que le sens positif est dans le sens des aiguilles d’une montre. À $z=0$ (le point violet le plus à gauche), la distance euclidienne entre $\tilde{\vect{y}}$ et $\vect{y}^{(23)}$ se traduit en grande partie par une énergie élevée. Lorsque $z$ s’approche de ${\pi}$ (le point violet le plus à droite), $\tilde{\vect{y}}$ se rapproche de $\vect{y}^{(23)}$, ce qui réduit l’énergie vers un niveau minimum. Inversement, lorsque z augmente au-delà de ${\pi}$ vers 2${\pi}$, la distance entre $\tilde{\vect{y}}$ et $\vect{y}^{(23)}$ augmente, et donc l’énergie augmente également vers un maximum.

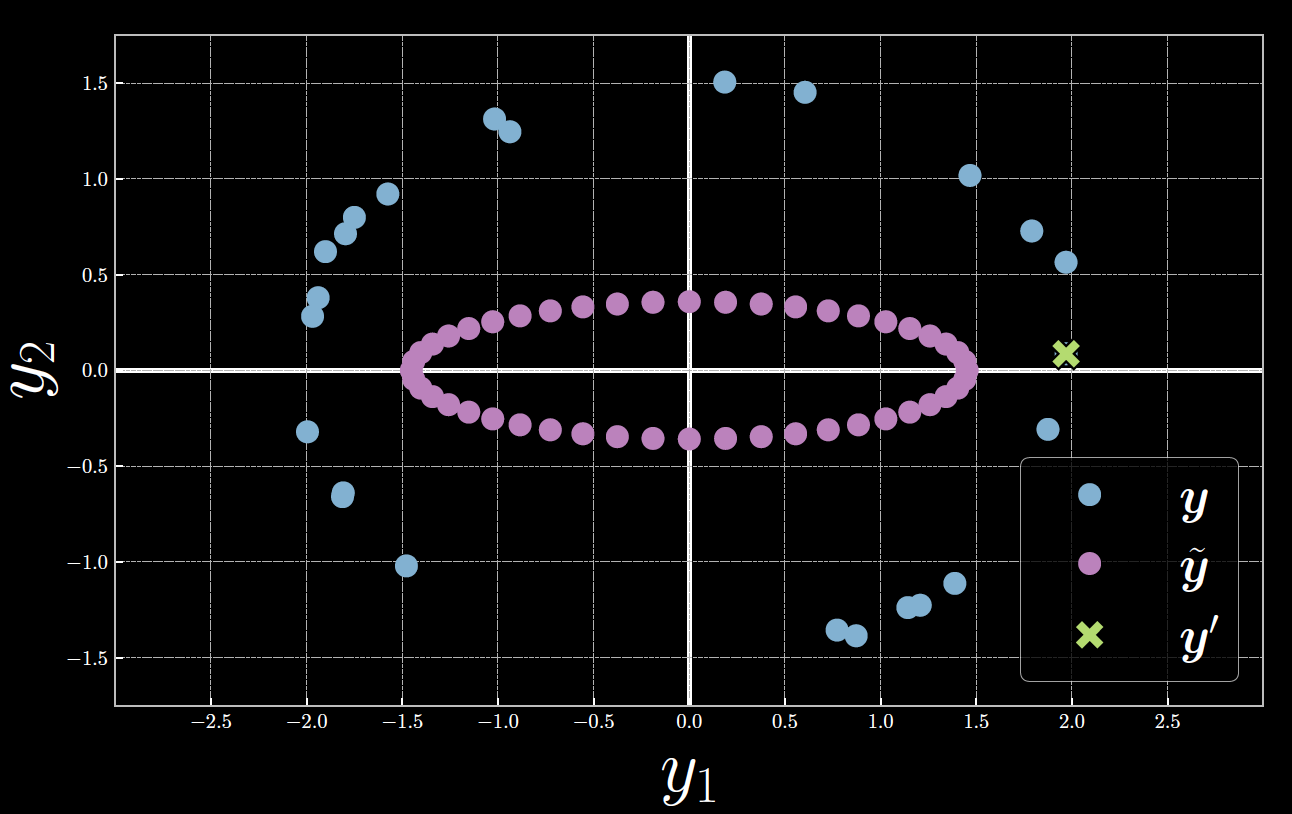
Figure 6 : Relation entre la variable latente, la sortie du décodeur et le 23ème échantillon

Maintenant que nous avons une compréhension de la distribution de l’énergie, évaluons la limite vers zéro de la température de l’énergie libre définie par ce qui suit :

Nous exprimerons également la variable latente qui donne l’énergie libre sous la forme $\check{z}$ définie par ce qui suit :

Comme le montre la figure 5, pour trouver l’énergie libre associée à $\vect{y}^{(23)}$, nous commençons par une variable initiale latente $\tilde{z}$. $\check{z}$ peut être évalué par des algorithmes d’optimisation tels que la recherche exhaustive, le gradient conjugué, la recherche linéaire ou le BFGS à mémoire limitée. L’énergie libre est la valeur minimale de l’énergie par rapport à la variable latente.

La figure 7 ci-dessous montre l’évaluation de l’énergie libre dans l’espace $\vect{y}$. Notons que tout au long de l’optimisation, la variable latente est augmentée de telle sorte que $\tilde{\vect{y}}$ se déplace dans le sens des aiguilles d’une montre vers $\vect{y}^{(23)}$. À l’énergie libre, l’énergie (et donc la distance entre $\tilde{\vect{y}}$ et $\vect{y}^{(23)}$) est minimisée.

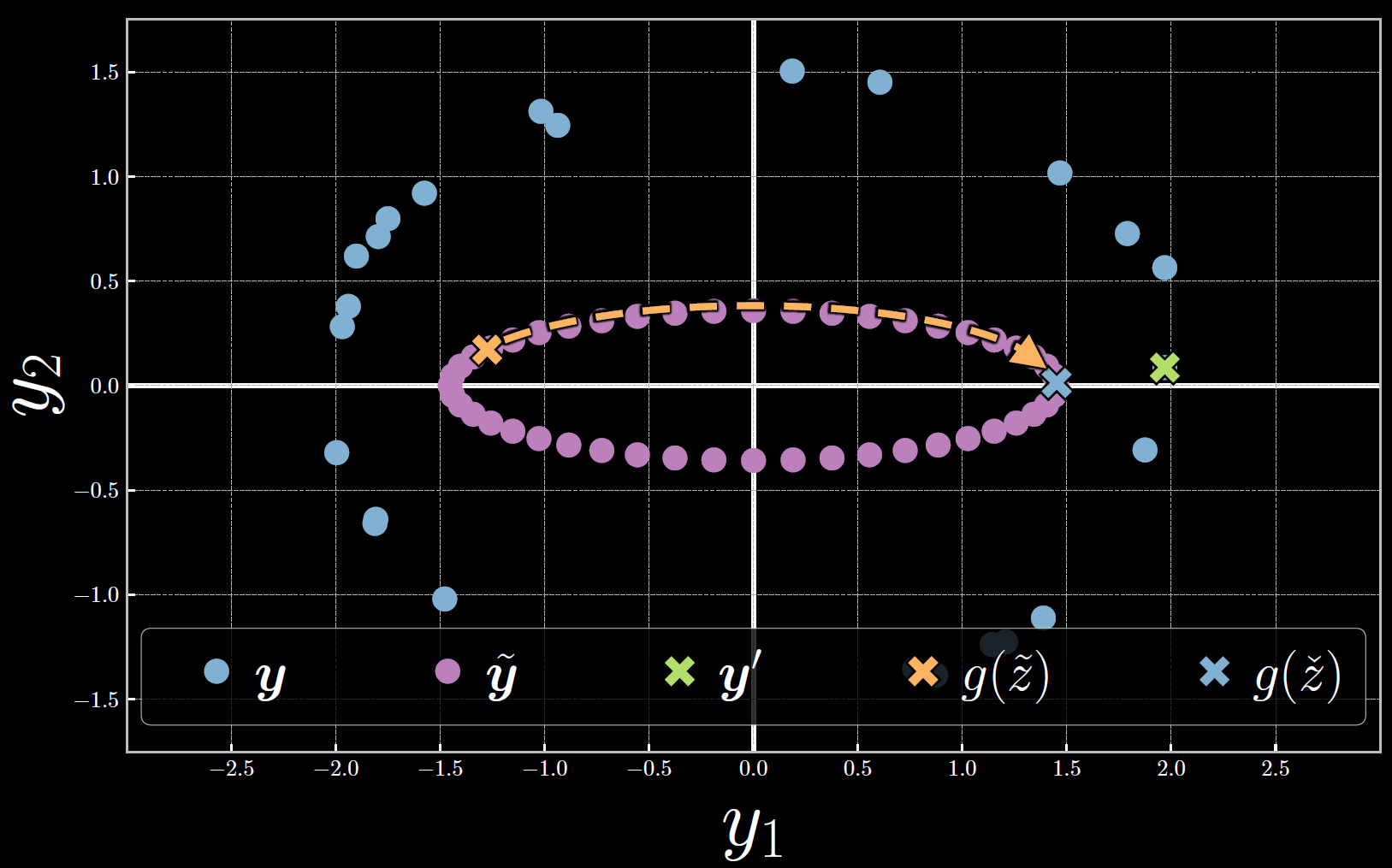
Figure 7 : Évaluation de l'énergie libre associée au 23ème échantillon

En évaluant l’énergie libre, $F_\infty$, et sa variable latente associée $\check{z}$, nous sommes capables de trouver le $\tilde{\vect{y}}$ décodé qui est proche des données de l’échantillon $\vect{y}^{(i)}$.

Estimation de la densité d’énergie libre

Pour mieux comprendre la fonction d’énergie libre, nous commençons par l’exemple présenté à la figure 8.

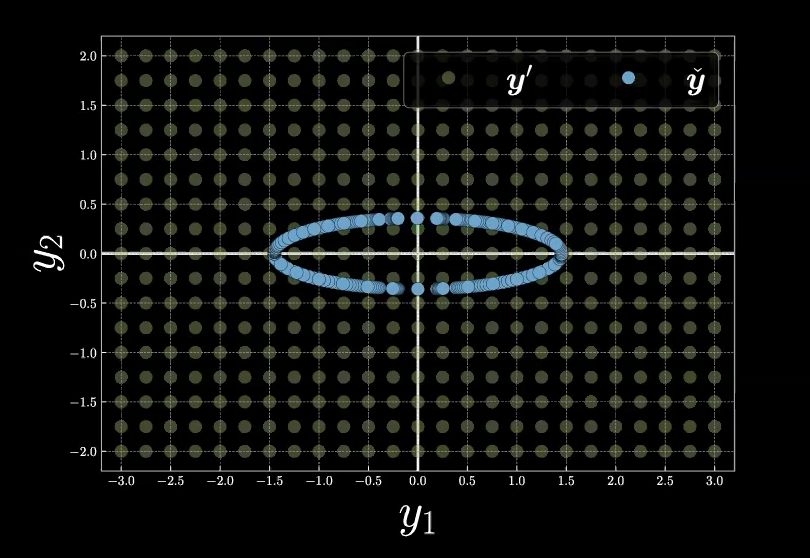
Figure 8 : Exemple d'énergie libre dans une grille de maille

Pour calculer l’énergie libre, $F_\infty$, à chaque point de la grille de maille par rapport à la variété en bleue (qui est également l’ensemble des choix possibles des variables latentes $z$), nous rappelons d’abord la définition de la fonction d’énergie libre ci-dessous :

Étant donné la formule de la fonction énergie $E(\vect{y},z)$ et un emplacement (un échantillon) $\vect{y}$, notre processus de minimisation commence par l’inférence qui est exactement le processus pour trouver la variable latente $\check{z}$ générant notre emplacement le plus probable. Sur le graphique de la figure 8, nous commençons par un point arbitraire $z$ sur la variété en bleue, puis nous nous déplaçons autour pour trouver sur la variété le point $\check{z}$ qui est le plus proche de notre emplacement $\vect{y}$. Par conséquent, l’énergie libre est la distance euclidienne entre notre point d’échantillonnage $\vect{y}$ et le point choisi $\tilde{\vect{y}}(\check{z})$.

Maintenant, nous considérons 5 points échantillons spécifiques dans la grille de maille, illustrés sur la figure 9 avec des couleurs différentes.

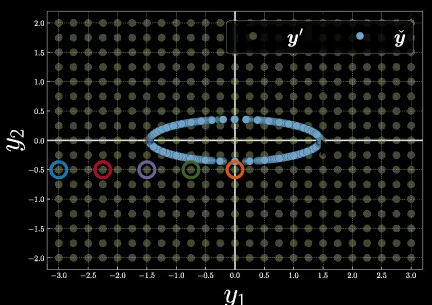
Figure 9 : Cinq points d'échantillonnage sur la grille de maille

Utilisons ce que nous avons appris ci-dessus et donnons une estimation des formes de la fonction d’énergie pour ces cinq points, par rapport aux différents choix de la variable latente $z$ sur la variété. Le point bleu est probablement la fonction d’énergie avec la plus grande magnitude et donc la plus grande énergie libre parmi les 5. Le point orange a probablement la plus petite énergie libre.

L’aspect complet des cinq fonctions d’énergie est donné comme suit dans la figure 10. Les signes en croix représentent les valeurs de $\check{z}$ pour chaque fonction d’énergie spécifique.

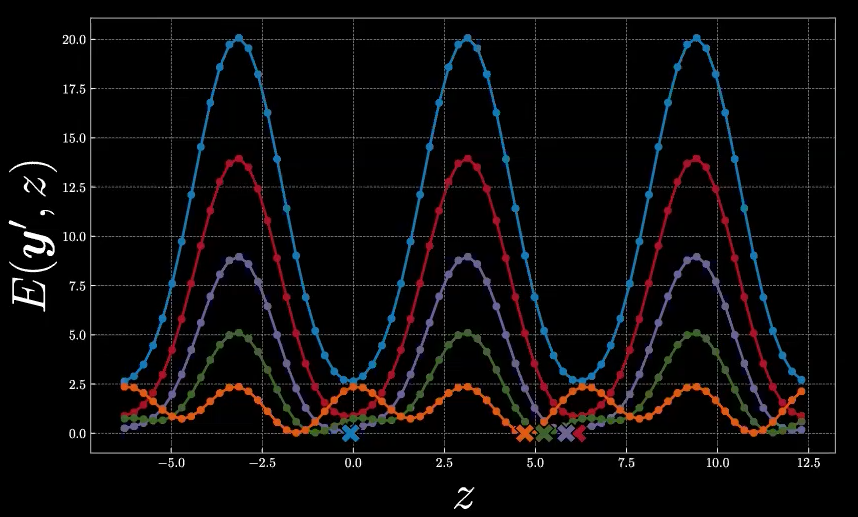
Figure 10 : Fonctions d’énergie pour les cinq points

En poursuivant l’exemple ci-dessus, nous devons noter que notre fonction d’énergie libre, $F_\infty$, ne prend que des valeurs scalaires non négatives pour son domaine (car nous utilisons la distance euclidienne pour $E(\vect{y},z)$). Le domaine de notre fonction d’énergie libre, $F_\infty$, est $\mathbb{R}^2$ (seulement l’espace $\vect{y}$), donc généralement nous avons $F_\infty : \mathbb{R}^2 \rightarrow \mathbb{R}^+$. Nous utilisons maintenant les valeurs d’énergie libre comme inférence pour tracer la grille de maille comme la carte thermique illustrée à la figure 11. À noter que les flèches représentent les valeurs de gradient.

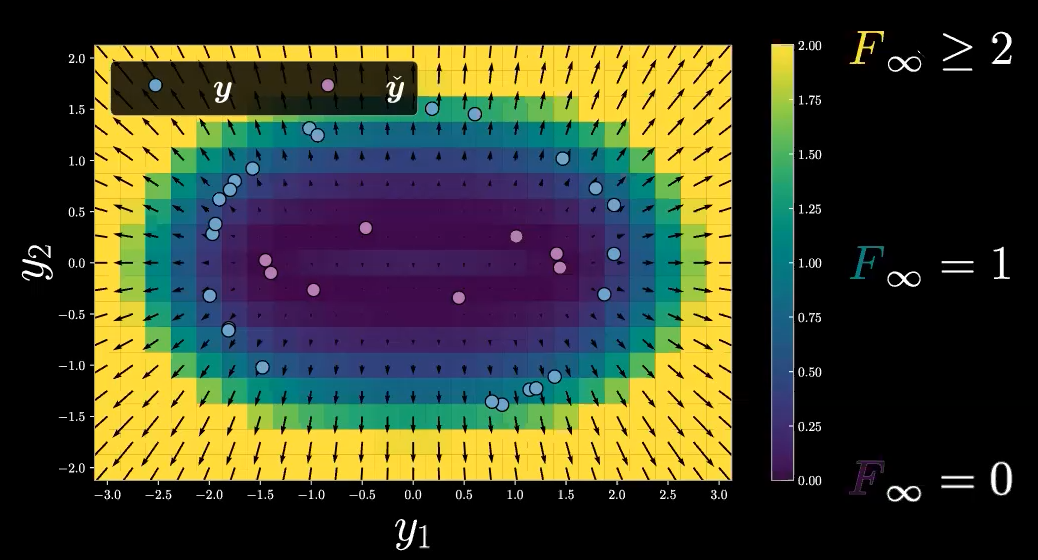
Figure 11 : Carte thermique de l’énergie libre

Pour résumer, nous ne discutons ici que d’un seul exemple d’énergie libre. Dans des circonstances réelles, nous aurons un choix beaucoup plus large de variables latentes $z$, plutôt que le seul choix de multiples ellipses dans notre exemple. Cependant, nous devons garder à l’esprit que la valeur de l’énergie libre, $F_\infty$, ne dépend pas du tout de la variable latente.

Réponses aux questions des étudiants

Question 1 : Pourquoi la surface énergétique est-elle évaluée de manière scalaire ?

La surface énergétique, qui prend la valeur de l’énergie libre $F_\infty$, est exactement la valeur minimale de notre fonction d’énergie $E(\vect{y},z)$ parmi toutes les variables latentes $z$ possibles. Par conséquent, $F_\infty$ ne dépend pas de $z$, mais seulement de $\vect{y}$, qui produit une valeur scalaire pour chaque choix de $\vect{y}$. En considérant l’exemple de maillage ci-dessus, celui-ci a $17\times 25 = 425$ points. Nous avons donc 425 valeurs d’énergie libre et chaque valeur est la distance euclidienne quadratique de chaque point de la variété.

Question 2 : Comment choisir la fonction pour représenter la variété ?

Il existe de nombreuses recherches sur les choix de la variable latente et nous pouvons avoir quelques couches de réseaux de neurones pour représenter les choix des variables latentes. Un exemple typique est celui de la traduction linguistique. Nous pouvons traduire une phrase de différentes manières et nous ne pouvons pas utiliser une fonction softmax pour l’entraînement de notre modèle car il y aura une infinité de phrases possibles après la traduction. Par conséquent, nous pouvons utiliser ici l’EBM et la fonction d’énergie nous dit dans quelle mesure la phrase originale et la phrase traduite sont compatibles.

Question 3 : Est-ce que la minimisation de l’énergie par rapport à la variété entraînée signifie-t-elle débruitage ?

Si le modèle a tiré des leçons de la variété réelle, vous pouvez trouver la version débruitée de votre entrée en minimisant l’énergie.