Modèles Génératifs et Auto-encodeurs variationnels

Récapitulatif : Auto-encodeur (AE)

Pour résumer l’auto-encodeur de manière très simple :

• Tout d’abord, l’auto-encodeur prend une entrée et l’associe à un état caché par une transformation affine $\boldsymbol{h} = f(\boldsymbol{W}_h \boldsymbol{x} + \boldsymbol{b}_h)$, où $f$ est une fonction d’activation (par élément). C’est l’étape de l’encodeur. Notons que $\boldsymbol{h}$ est également appelé le code.
• Ensuite, $\hat{\boldsymbol{x}} = g(\boldsymbol{W}_x \boldsymbol{h} + \boldsymbol{b}_x)$, où $g$ est une fonction d’activation. C’est l’étape du décodeur.

Pour une explication détaillée, voir les notes de la semaine 7.

Intuition derrière les VAEs et comparaison avec les auto-encodeurs classiques

Ensuite, nous présentons les auto-encodeurs variationnels (VAEs), un type de modèles génératifs. Mais pourquoi s’intéresser aux modèles génératifs ? Pour répondre à la question, les modèles discriminants apprennent à faire des prédictions à partir de certaines observations, mais les modèles génératifs visent à simuler le processus de génération de données. Un des effets est que les modèles génératifs peuvent mieux comprendre les relations causales sous-jacentes, ce qui conduit à une meilleure généralisation.

Il est à noter que bien que le nom VAE contienne le terme « auto-encodeurs » (AE) en raison de la similarité structurelle ou architecturale avec les auto-encodeurs, les formulations entre VAE et AE sont très différentes.

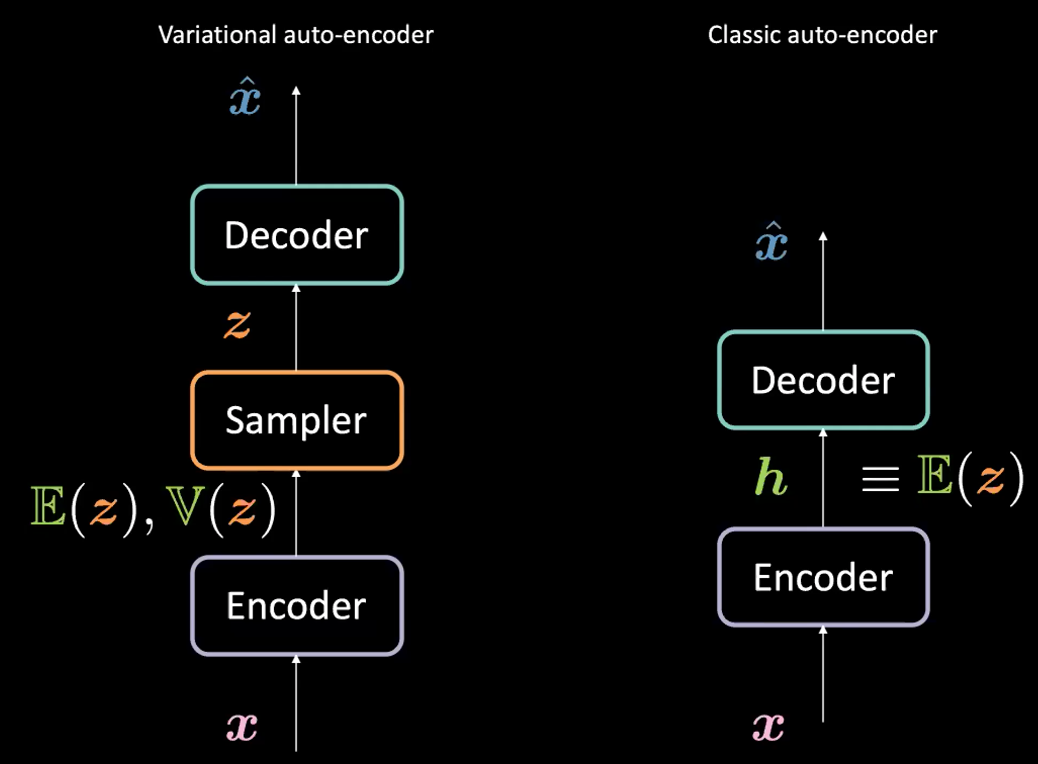
Figure 1 : VAE vs AE classique

Quelle est la différence entre l’auto-encodeur variationnel (VAE) et l’auto-encodeur classique (AE) ?

Pour le VAE :

• D’abord, l’étape de l’encodeur : nous passons l’entrée $\boldsymbol{x}$ à l’encodeur. Au lieu de générer une représentation cachée $\boldsymbol{h}$ (le code) dans AE, le code dans VAE comprend deux choses : $\mathbb{E}(\boldsymbol{z})$ et $\mathbb{V}(\boldsymbol{z})$ où $\boldsymbol{z}$ est la variable aléatoire latente suivant une distribution gaussienne avec la moyenne $\mathbb{E}(\boldsymbol{z})$ et la variance $\mathbb{V}(\boldsymbol{z})$. A noter qu’en pratique, les gens utilisent les distributions gaussiennes comme distribution encodée, mais d’autres distributions peuvent également être utilisées. L’encodeur sera une fonction de $\mathcal{X}$ à $\mathbb{R}^{2d}$ : $\boldsymbol{x} \mapsto \boldsymbol{h}$ (ici nous utilisons $\boldsymbol{h}$ pour représenter la concaténation de $\mathbb{E}(\boldsymbol{z})$ et $\mathbb{V}(\boldsymbol{z})$).
• Ensuite, nous allons échantillonner $\boldsymbol{z}$ à partir de la distribution ci-dessus paramétrée par l’encodeur. Plus précisément, $\mathbb{E}(\boldsymbol{z})$ et $\mathbb{V}(\boldsymbol{z})$ sont passés dans un échantillonneur pour générer la variable latente $\boldsymbol{z}$.
• Ensuite, $\boldsymbol{z}$ est passé dans le décodeur pour générer $\hat{\boldsymbol{x}}$.
• Le décodeur sera une fonction de $\mathcal{Z}$ vers $\mathbb{R}^{n}$: $\boldsymbol{z} \mapsto \boldsymbol{\hat{x}}$.

En fait, pour l’auto-encodeur classique, on peut considérer $\boldsymbol{h}$ comme le vecteur $\E(\boldsymbol{z})$ de la formulation VAE. En bref, la principale différence entre les VAEs et les AEs est que les VAEs ont un bon espace latent qui permet le processus de génération.

La fonction de perte des VAEs

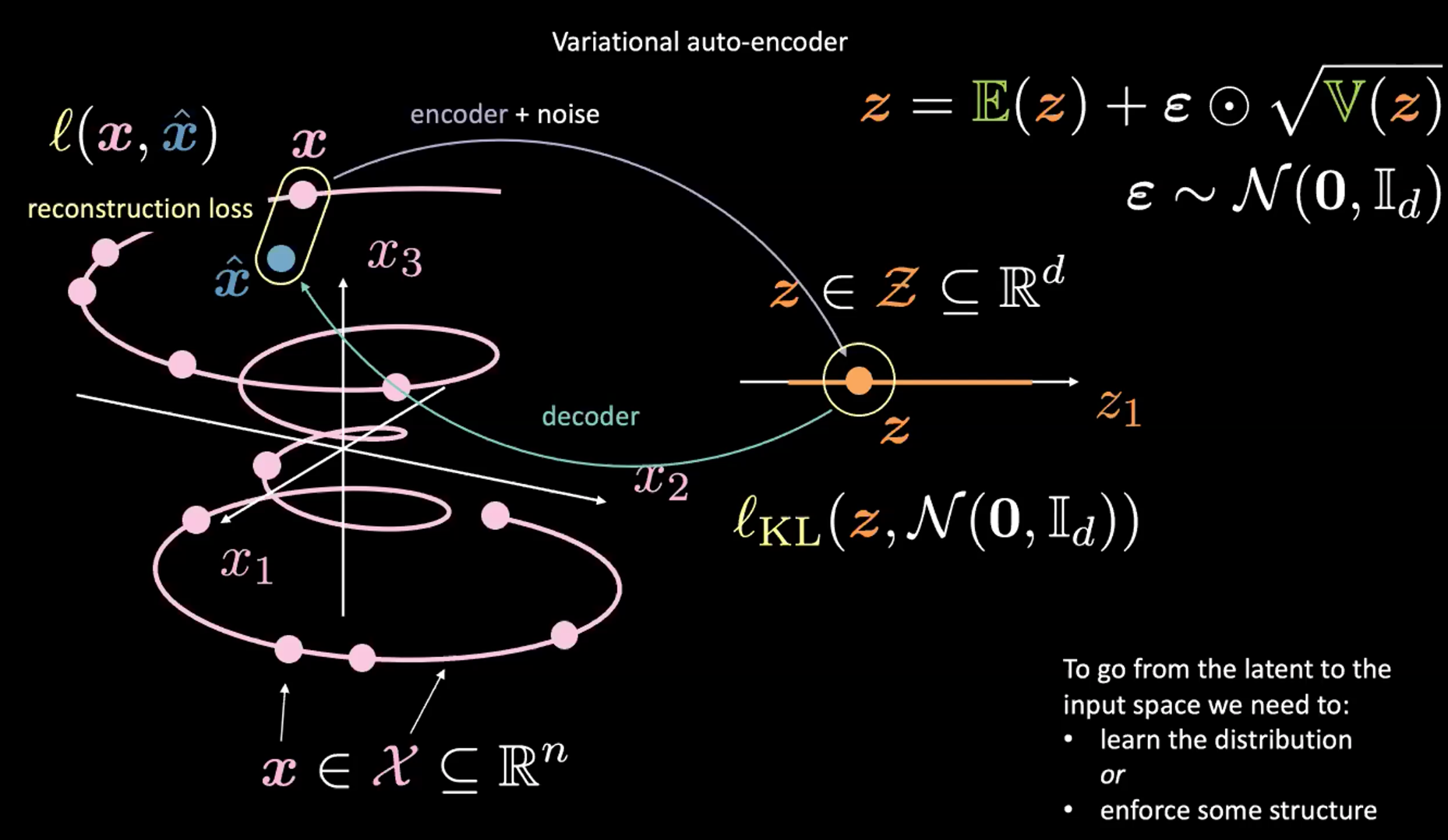
Figure 2 : De l'espace d'entrée vers l'espace latent

Décrivons cette figure 2 ci-dessus. Commençons par ignorer le coin supérieur droit (qui est l’astuce de reparamétrage expliquée dans la section suivante).

D’abord nous encodons, de l’espace d’entrée (à gauche) à l’espace latent (à droite), en passant par l’encodeur et le bruit. Ensuite, nous décodons de l’espace latent (à droite) à l’espace de sortie (à gauche). Pour passer de l’espace latent à l’espace d’entrée (le processus de génération), nous devrons soit apprendre la distribution (du code latent), soit appliquer une certaine structure. Dans notre cas, le VAE applique une certaine structure à l’espace latent.

Comme d’habitude, pour entraîner le VAE, nous minimisons une fonction de perte. La fonction de perte est donc composée d’un terme de reconstruction ainsi que d’un terme de régularisation.

• Le terme de reconstruction se trouve sur la dernière couche (côté gauche de la figure). Cela correspond à $l(\boldsymbol{x}, \hat{\boldsymbol{x}})$ dans la figure.
• Le terme de régularisation se trouve sur la couche latente, pour renforcer une structure gaussienne spécifique sur l’espace latent (côté droit de la figure). Pour ce faire, nous utilisons un terme de pénalité $l_{KL}(\boldsymbol{z}, \mathcal{N}(\boldsymbol{0}, \boldsymbol{I}_d))$. Sans ce terme, le VAE agira comme un auto-encodeur classique, ce qui peut conduire à du surentraînement et nous n’aurons pas les propriétés génératrices que nous souhaitons.

Discussion sur l’échantillonnage $\boldsymbol{z}$ (astuce de paramétrage)

Comment prélever un échantillon de la distribution renvoyée par l’encodeur dans la VAE ? Selon ce qui précède, nous effectuons un échantillonnage à partir de la distribution gaussienne, afin d’obtenir $\boldsymbol{z}$. Cependant, cela est problématique, car lorsque nous effectuons une descente de gradient pour entraîner le modèle VAE, nous ne savons pas comment effectuer la rétropropagation par le module d’échantillonnage.

Nous utilisons plutôt l’astuce du reparamétrage pour échantillonner $\boldsymbol{z}$. Nous utilisons $\boldsymbol{z} = \mathbb{E}(\boldsymbol{z}) + \boldsymbol{\epsilon} \odot \sqrt{\mathbb{V}(\boldsymbol{z})}$ où $\epsilon\sim \mathcal{N}(\boldsymbol{0}, \boldsymbol{I}_d)$. Dans ce cas, la rétropropagation lors de l’entraînement est possible. Plus précisément, les gradients passeront par la multiplication (par élément) et l’addition dans l’équation ci-dessus.

Rompre la fonction de perte des VAEs

Visualisation des estimations de variables latentes et de la perte de reconstruction

Comme indiqué ci-dessus, la fonction de perte pour le VAE comporte deux parties : un terme de reconstruction et un terme de régularisation. On peut écrire cela comme :

Pour visualiser l’objectif de chaque terme dans la fonction de perte, nous pouvons penser à chaque valeur estimée de $\boldsymbol{z}$ comme un cercle dans un espace de $2d$, où le centre du cercle est $\mathbb{E}(\boldsymbol{z})$ et la zone environnante sont les valeurs possibles de $\boldsymbol{z}$ déterminées par $\mathbb{V}(\boldsymbol{z})$.

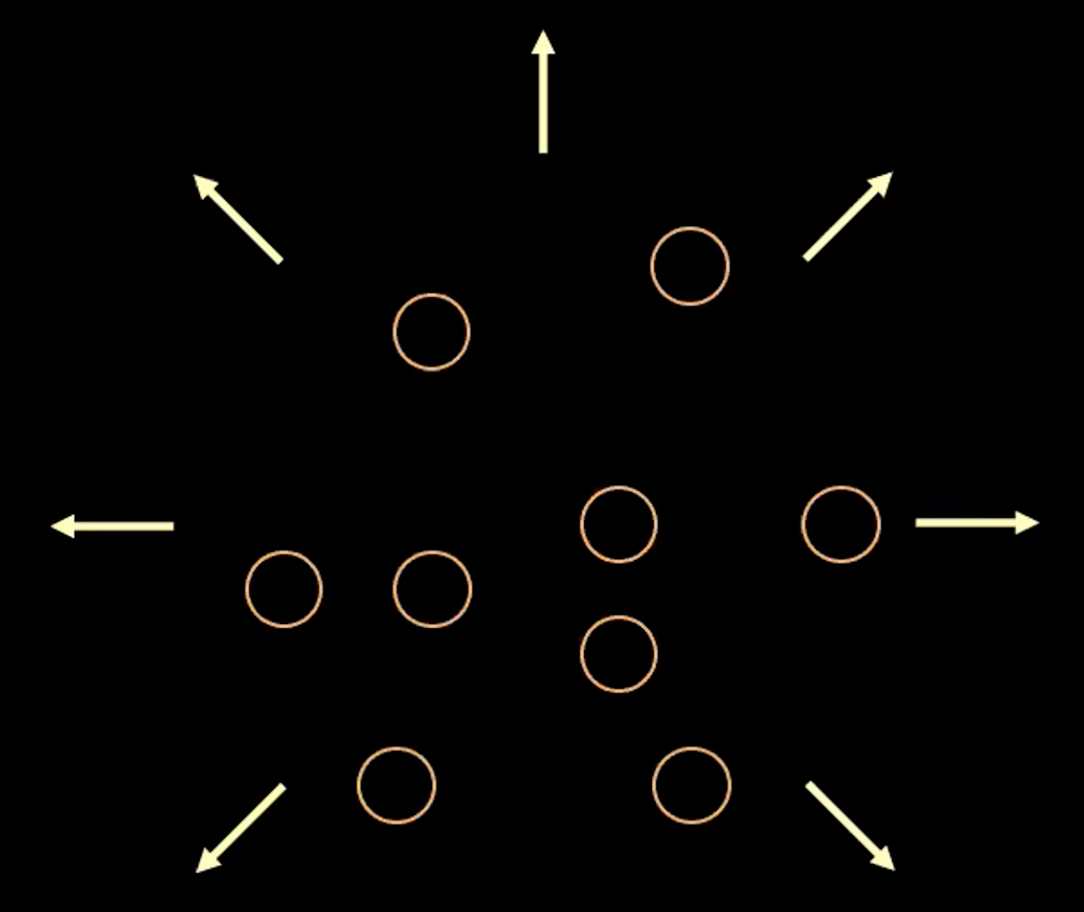
Figure 3 : Visualisation du vecteur $z$ sous forme de bulles dans l'espace latent

Dans la figure 3 ci-dessus, chaque bulle représente une région estimée à $\boldsymbol{z}$ et les flèches représentent comment le terme de reconstruction éloigne chaque valeur estimée des autres, ce qui est expliqué plus en détail ci-dessous.

S’il y a un chevauchement entre deux estimations de $z$, (visuellement si deux bulles se chevauchent), cela crée une ambiguïté pour la reconstruction car les points de chevauchement peuvent être mis en correspondance avec les deux entrées originales. Par conséquent, la perte de reconstruction éloignera les points l’un de l’autre.

Cependant, si nous n’utilisons que la perte de reconstruction, les estimations continueront à être éloignées l’une de l’autre et le système pourrait exploser. C’est là qu’intervient le terme de pénalité.

Note : pour les entrées binaires, la perte de reconstruction est :

et pour les entrées ayant une valeur réelle, la perte de reconstruction est :

Le terme de pénalité

Le deuxième terme est l’entropie relative (une mesure de la distance entre deux distributions) entre $\boldsymbol{z}$ qui provient d’une gaussienne avec la moyenne $\mathbb{E}(\boldsymbol{z})$, la variance $\mathbb{V}(\boldsymbol{z})$ et la distribution normale standard. Si nous élargissons ce deuxième terme dans la fonction de perte du VAE, nous obtenons

Chaque expression de la somme comporte quatre termes. Ci-dessous, nous écrivons les trois premiers termes dans la figure 4 et nous les reportons sur un graphique.

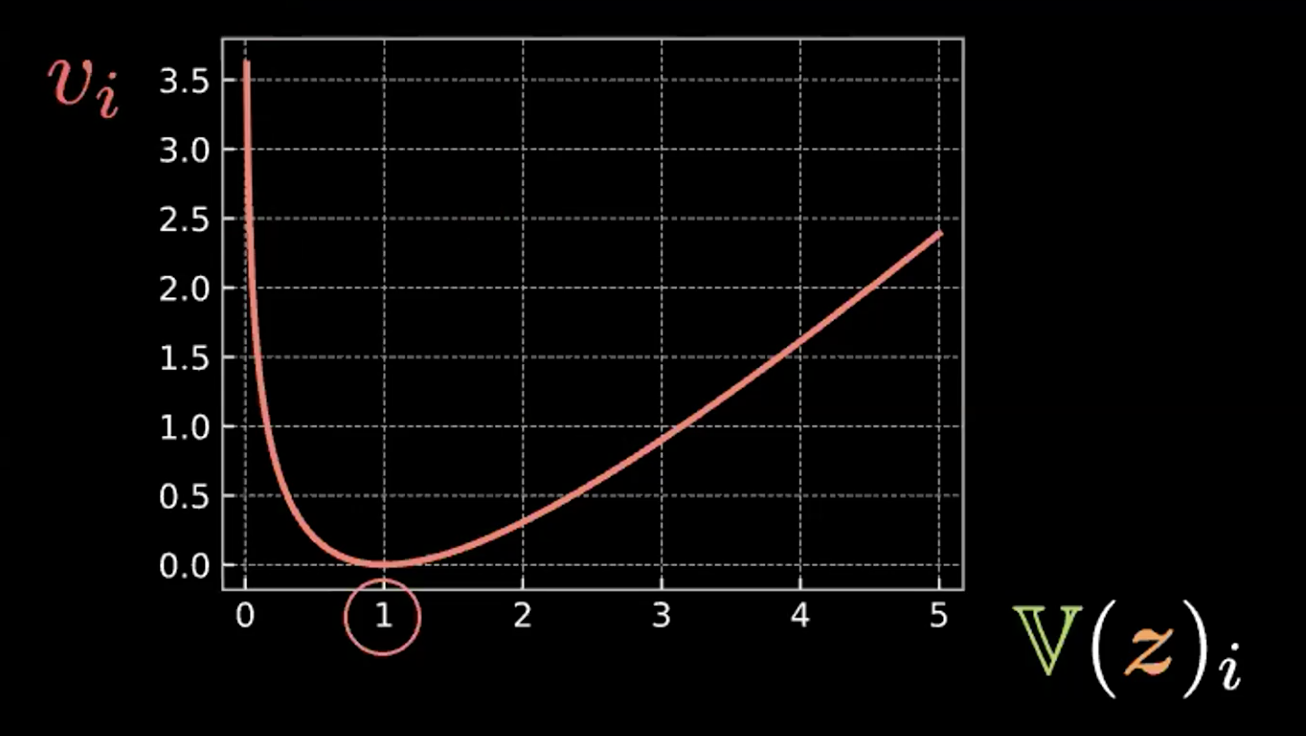
Figue 4 : Graphique montrant comment l'entropie relative force les bulles à avoir une variance de 1

On peut donc voir que cette expression est minimisée lorsque $z_i$ a la variance à 1. Par conséquent, notre perte de pénalité maintiendra la variance de nos variables latentes estimées à environ 1. Visuellement, cela signifie que nos « bulles » du haut auront un rayon d’environ 1.

Le dernier terme, $\mathbb{E}(z_i)^2$, minimise la distance entre les $z_i$ et empêche donc l’explosion favorisée par le terme de reconstruction.

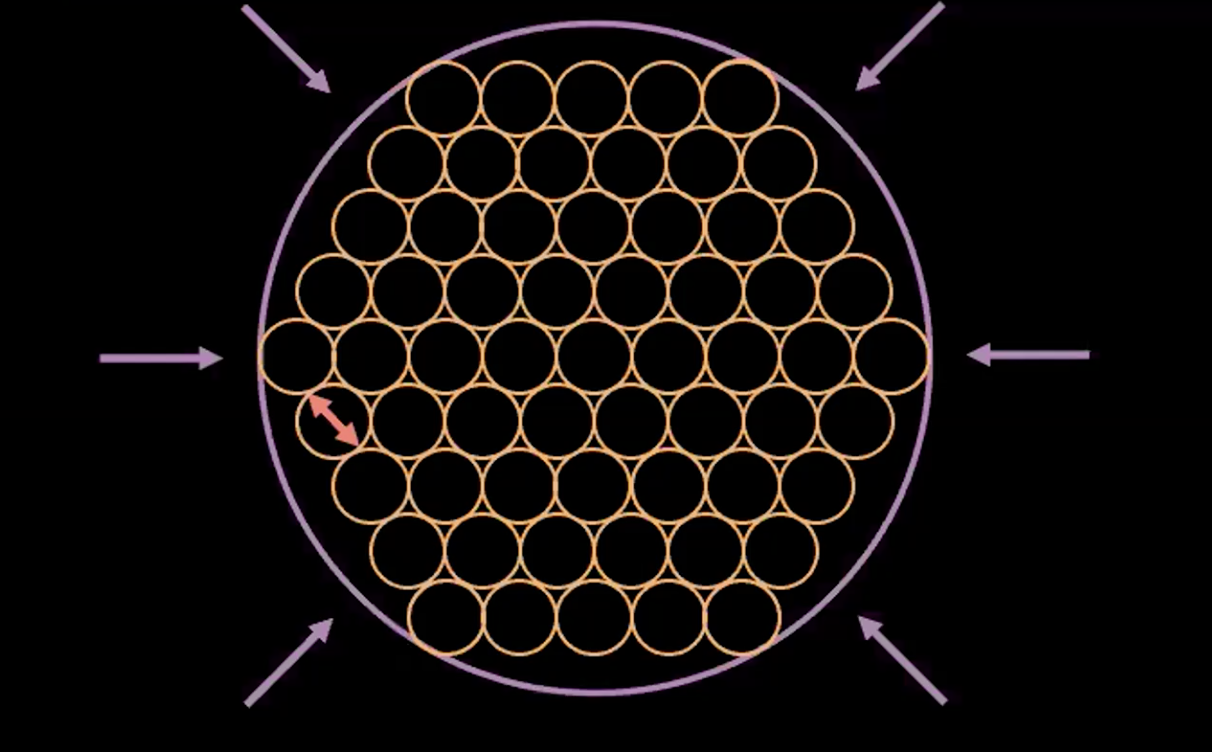
Figure 5 : L'interprétation « bulle-de-bulle » du VAE

La figure 5 ci-dessus montre comment la perte du VAE a poussé les variables latentes estimées aussi près que possible l’une de l’autre sans aucun chevauchement tout en maintenant la variance estimée de chaque point autour de 1.

Note : le $\beta$ dans la fonction de perte du VAE est un hyperparamètre qui dicte comment pondérer les termes de reconstruction et de pénalité.

Implémentation de l’auto-encodeur variationnel (VAE)

La version anglaise du notebook Jupyter se trouve ici et celle en français ici.

Dans ce notebook, nous implémentons un VAE et nous l’entraînons sur le jeu de données MNIST. Ensuite, nous échantillonnons $\boldsymbol{z}$ à partir d’une distribution normale et l’envoyons au décodeur pour comparer le résultat. Enfin, nous examinons comment $\boldsymbol{z}$ change dans la projection 2D.

Note : dans le jeu de données MNIST utilisé, les valeurs des pixels ont été normalisées pour se situer dans la plage $[0, 1]$.

L’encodeur et le décodeur

1. Nous définissons l’encodeur et le décodeur dans notre module VAE.
2. Pour la dernière couche linéaire de l’encodeur, nous définissons la sortie comme étant de taille $2d$, dont les premières valeurs $d$ sont les moyennes et les autres valeurs $d$ sont les variances. Nous échantillonnons $\boldsymbol{z} \in R^d$ en utilisant ces moyennes et variances comme expliqué dans l’astuce de reparamétrage précédente.
3. Pour la dernière couche linéaire dans le décodeur, nous utilisons l’activation sigmoïde afin de pouvoir avoir une sortie dans la plage $[0, 1]$, similaire aux données d’entrée.

class VAE(nn.Module):
    def __init__(self):
        super().__init__()

        self.encoder = nn.Sequential(
            nn.Linear(784, d ** 2),
            nn.ReLU(),
            nn.Linear(d ** 2, d * 2)
        )

        self.decoder = nn.Sequential(
            nn.Linear(d, d ** 2),
            nn.ReLU(),
            nn.Linear(d ** 2, 784),
            nn.Sigmoid(),
        )

Reparamétrage et fonction forward

Pour la fonction reparameterise, si le modèle est en mode entraînement, nous calculons l’écart-type (std) de la variance logarithmique (logvar). Nous utilisons la variance logarithmique au lieu de la variance parce que nous voulons nous assurer que la variance n’est pas négative, et le fait de prendre le logarithme de celle-ci nous assure d’avoir la gamme complète de la variance, ce qui entraîne une plus grande stabilité de l’apprentissage.

Pendant l’entraînement, la fonction reparameterise permet de faire l’astuce permettant la rétropropagation. Pour faire le lien avec le concept de la bulle jaune, chaque fois que cette fonction est appelée, nous dessinons un point eps = std.data.new(std.size()).normal_(). Donc si nous le faisons 100 fois, nous obtenons 100 points qui forment approximativement une sphère parce que c’est une distribution normale et la ligne eps.mul(std).add_(mu) fait que cette sphère est centrée en mu avec un rayon égal à std.

Pour la fonction forward, nous calculons d’abord mu (première moitié) et le logvar (seconde moitié) à partir de l’encodeur, puis nous calculons le symbole $\boldsymbol{z}$ via la fonction reparamterise. Enfin, nous renvoyons la sortie du décodeur.

def reparameterise(self, mu, logvar):
    if self.training:
        std = logvar.mul(0.5).exp_()
        eps = std.data.new(std.size()).normal_()
        return eps.mul(std).add_(mu)
    else:
        return mu

def forward(self, x):
    mu_logvar = self.encoder(x.view(-1, 784)).view(-1, 2, d)
    mu = mu_logvar[:, 0, :]
    logvar = mu_logvar[:, 1, :]
    z = self.reparameterise(mu, logvar)
    return self.decoder(z), mu, logvar

Fonction de perte pour le VAE

Nous définissons ici la perte de reconstruction (entropie binaire croisée) et l’entropie relative (pénalité de divergence KL).

def loss_function(x_hat, x, mu, logvar):
    BCE = nn.functional.binary_cross_entropy(
        x_hat, x.view(-1, 784), reduction='sum'
    )
    KLD = 0.5 * torch.sum(logvar.exp() - logvar - 1 + mu.pow(2))

    return BCE + KLD

Générer de nouveaux échantillons

Après avoir entraîné notre modèle, nous pouvons échantillonner un $z$ aléatoire de la distribution normale et l’envoyer à notre décodeur. Nous pouvons observer sur la figure 6 que certains des résultats ne sont pas bons parce que notre décodeur n’a pas couvert tout l’espace latent. Cela peut être amélioré si nous entraînons le modèle pour d’autres époques.

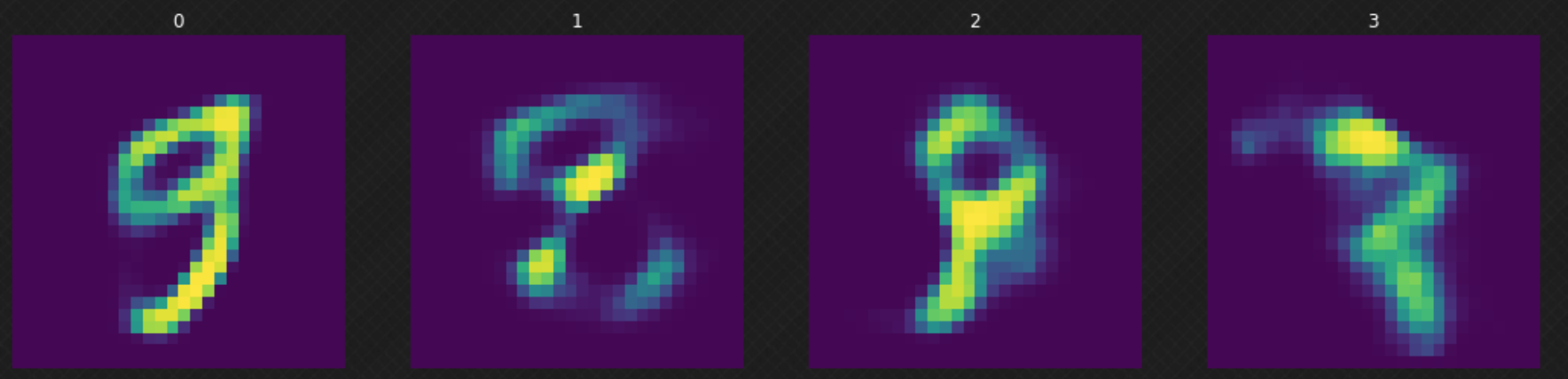
Figure 6 : Déplacement aléatoire dans l'espace latent

Nous pouvons voir comment un chiffre se transforme en un autre, ce qui n’aurait pas été possible si nous avions utilisé un auto-encodeur. Nous pouvons voir que lorsque nous marchons dans l’espace latent, la sortie du décodeur semble toujours légitime. La figure 7 ci-dessous montre comment nous transformons le chiffre $3$ en $8$.

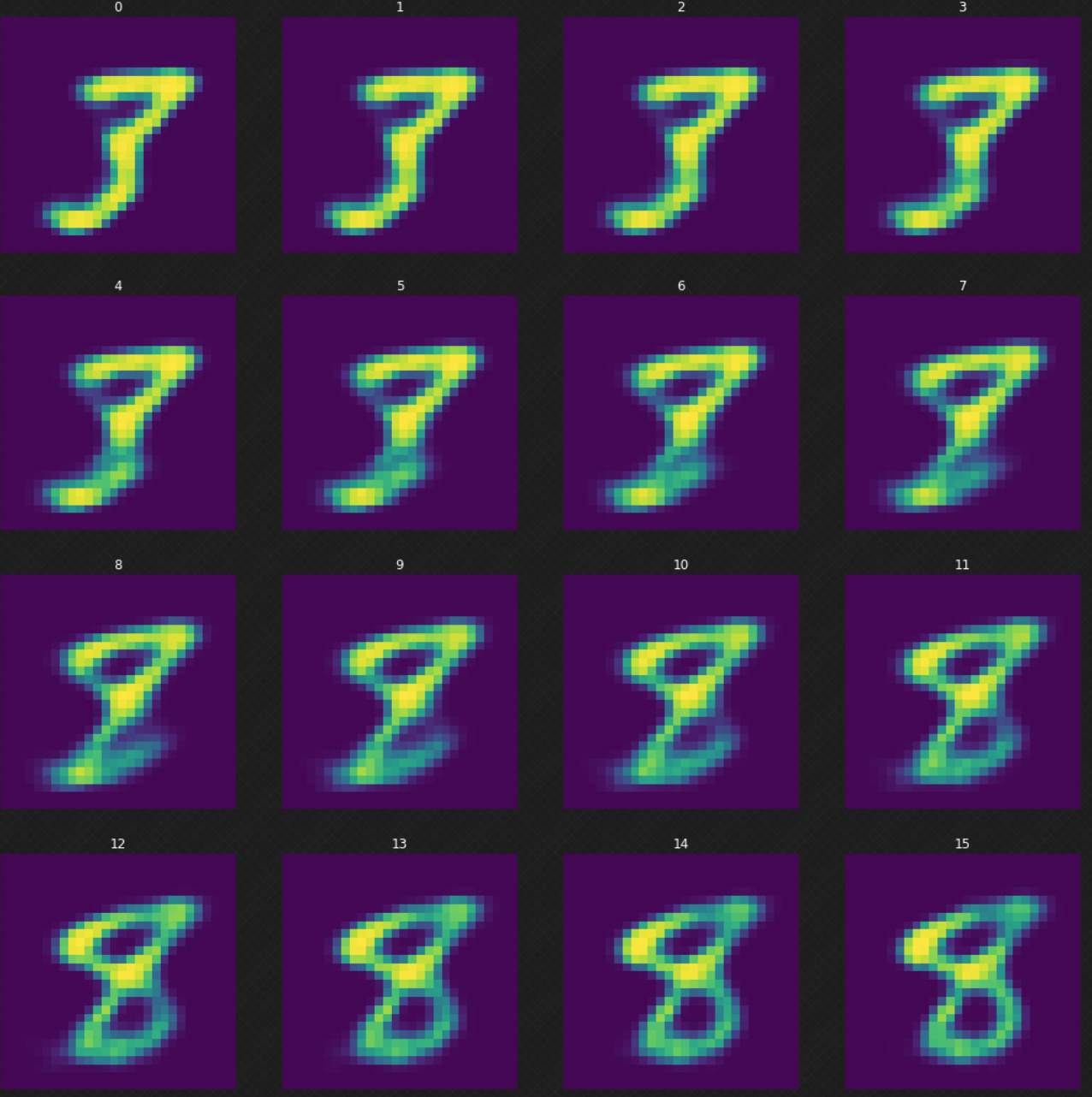
Figure 7 : Transformation du chiffre 3 en 8

Projection des moyennes

Enfin, examinons comment l’espace latent change pendant ou après l’entraînement. Les graphiques de la figure 8 sont les moyennes issues de la sortie de l’encodeur, projetées sur l’espace 2D, où chaque couleur représente un chiffre. Nous pouvons voir qu’à partir de l’époque 0, les classes se répandent partout, avec une faible concentration. Au fur et à mesure que le modèle est entraîné, l’espace latent devient plus défini et les classes (chiffres) commencent à former des groupes.

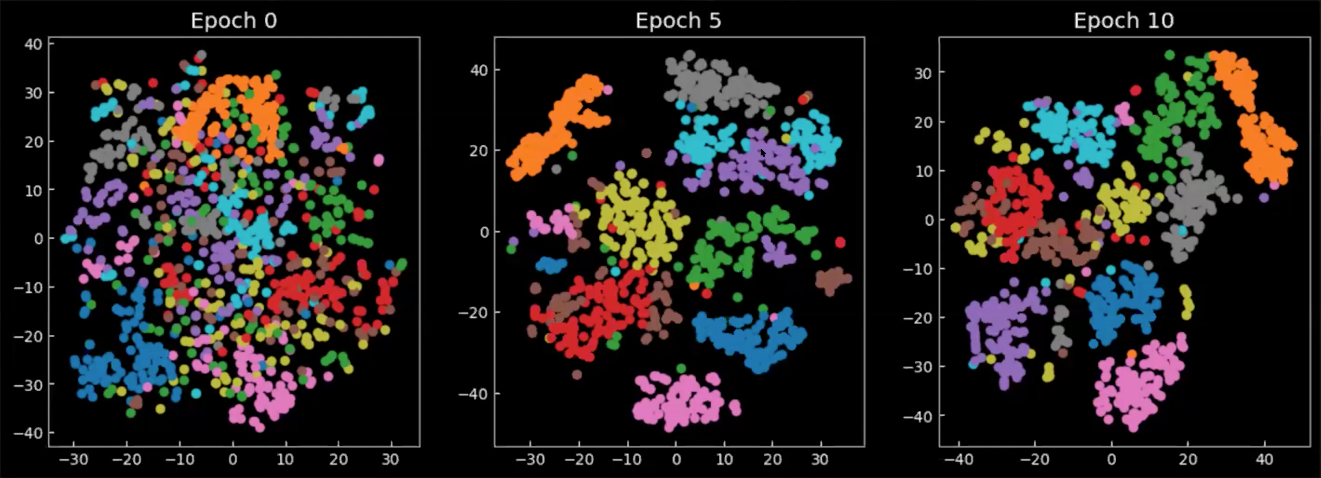
Figure 8 : Projection 2D des moyennes $\E(\vect{z})$ dans l'espace latent