EBMs à variables latentes régularisées

EBMs à variables latentes régularisées

Les modèles avec des variables latentes sont capables de faire une distribution de prédictions $\overline{y}$ conditionnée par une entrée observée $x$ et une variable latente supplémentaire $z$. Les modèles à base d’énergie peuvent également contenir des variables latentes :

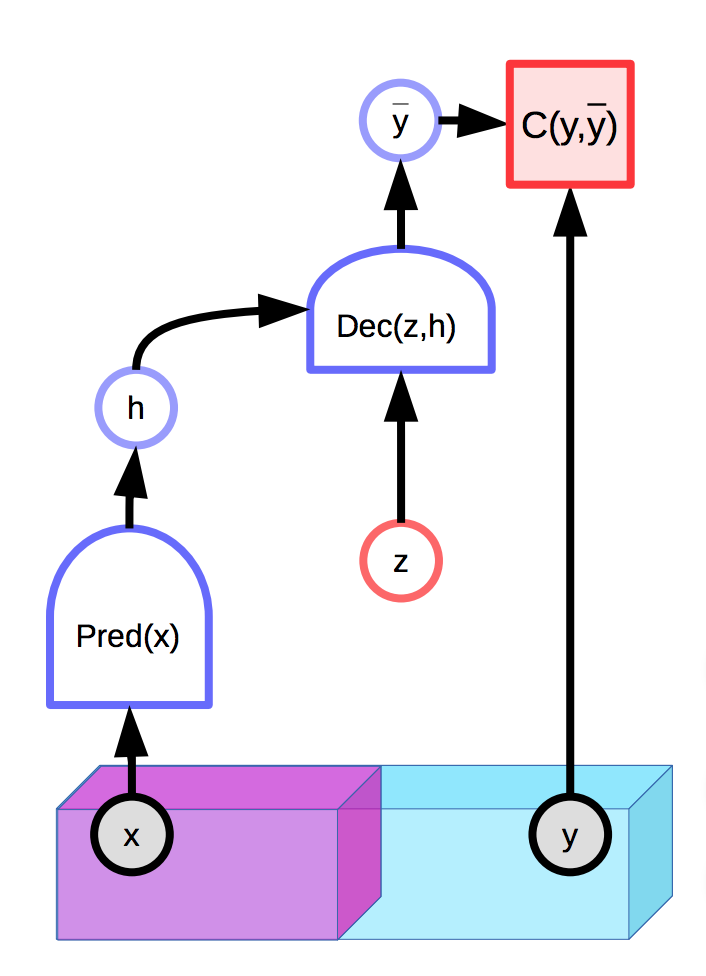
Figure 1 : Exemple d'un EBM à variable latente

Malheureusement, si la variable latente $z$ a une trop grande puissance expressive dans la production de la prédiction finale $\overline{y}$, chaque sortie réelle $y$ sera parfaitement reconstruite à partir de l’entrée $x$ avec un $z$ choisi de manière appropriée. Cela signifie que la fonction d’énergie sera partout égale à 0, puisque l’énergie est optimisée à la fois sur $y$ et $z$ pendant l’inférence.

Une solution naturelle consiste à limiter la capacité d’information de la variable latente $z$. Un moyen d’y parvenir est de régulariser la variable latente :

Cette méthode limite le volume de l’espace de $z$ qui prend une petite valeur et la valeur qui, à son tour, contrôle l’espace de $y$ ayant une faible énergie. La valeur de $\lambda$ contrôle ce compromis. Un exemple utile de $R$ est la norme $L_1$, qui peut être considérée comme une approximation différenciable de la dimension effective presque partout. Ajouter du bruit à $z$ tout en limitant sa norme $L_2$ peut également limiter son contenu en information (VAE).

Codage épars

Le codage épars est un exemple d’EBM à variables latentes régularisées inconditionnelles qui tente essentiellement d’approcher les données avec une fonction linéaire par morceaux :

Le vecteur $z$ de dimension $n$ a tendance à avoir un nombre maximum de composantes non nulles $m « n$. Chaque $Wz$ est donc constitué d’éléments dans l’intervalle des $m$ colonnes de $W$.

Après chaque étape d’optimisation, la matrice $W$ et la variable latente $z$ sont normalisées par la somme des normes $L_2$ des colonnes de $W$. Cela garantit que $W$ et $z$ ne divergent pas à l’infini et à zéro.

FISTA

Figure 2 : Graphe de calcul de FISTA

FISTA (fast ISTA) est un algorithme qui optimise la fonction d’énergie de codage épars $E(y,z)$ par rapport à $z$ en optimisant alternativement les deux termes $\Vert y - Wz\Vert^2$ et $\lambda \Vert z\Vert_{L^1}$. Nous initialisons $Z(0)$ et mettons à jour itérativement $Z$ selon la règle suivante :

L’expression interne $Z(t) - \frac{1}{L}W_d^\top(W_dZ(t) - Y)$ est un pas de gradient pour le terme $\Vert y - Wz\Vert^2$. La fonction $\text{Shrinkage}$ décale ensuite les valeurs vers 0, ce qui optimise le terme $\lambda \Vert z\Vert_{L_1}$.

LISTA

FISTA est trop coûteux pour être appliqué à des jeux de données de grandes dimensions (par exemple les images). Un moyen de le rendre plus efficace est d’entraîner un réseau à prédire la variable latente optimale $z$ :

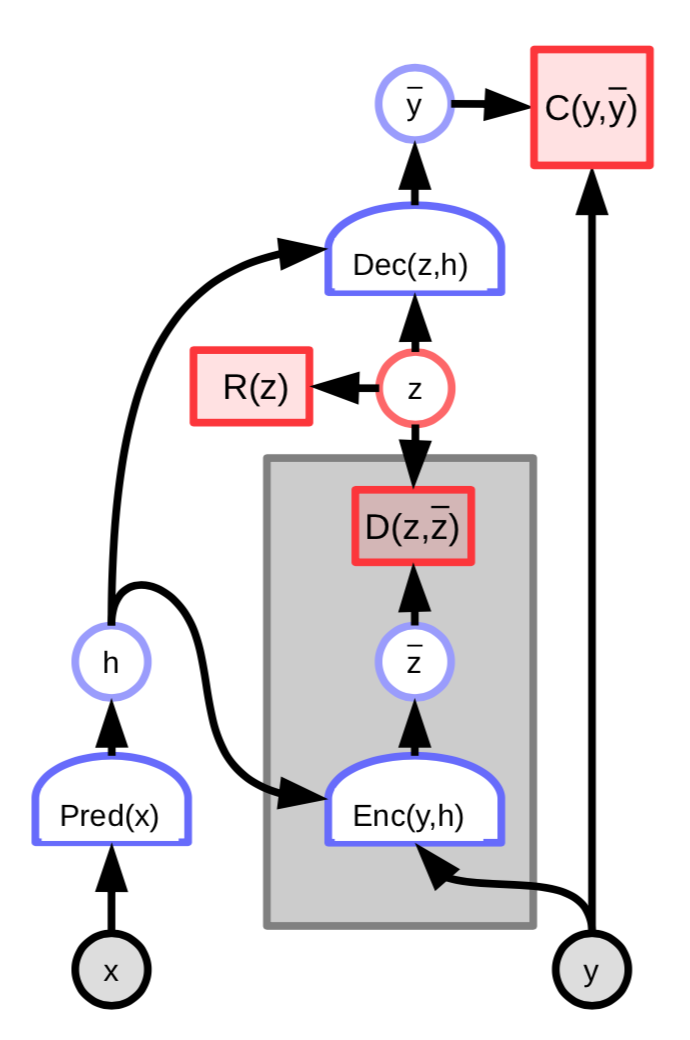
Figure 3 : Encodeur d'un EBM à variables latentes

L’énergie de cette architecture comprend alors un terme supplémentaire qui mesure la différence entre la variable latente prédite $\overline z$ et la variable latente optimale $z$ :

Nous pouvons définir plus précisément

et ensuite écrire

Cette règle de mise à jour peut être interprétée comme un réseau récurrent, ce qui suggère que nous pouvons apprendre les paramètres $W_e$ qui déterminent itérativement la variable latente $z$. Le réseau est exécuté pour un nombre de pas de temps $K$ fixe et les gradients de $W_e$ sont calculés en utilisant la rétropropagation standard à travers le temps. Le réseau entraîné produit alors un bon $z$ en moins d’itérations que l’algorithme FISTA.

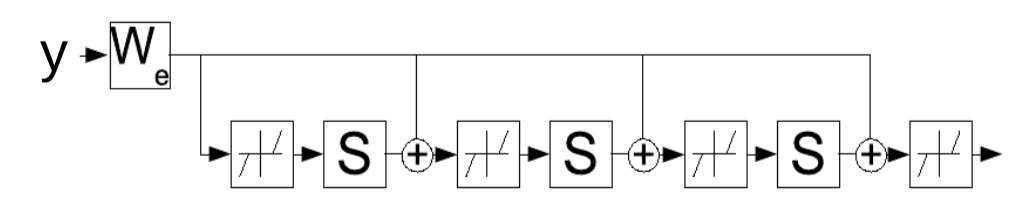
Figure 4 : LISTA comme un réseau récurrent déployé à travers le temps

Exemples de codage épars

Lorsqu’un système de codage épars avec un vecteur latent à 256 dimensions est appliqué aux chiffres manuscrits de MNIST, le système apprend un ensemble de 256 traits qui peuvent être combinés linéairement pour reproduire presque tout l’ensemble d’entraînement. Le régularisateur épars garantit qu’ils peuvent être reproduits à partir d’un petit nombre de traits.

Figure 5 : Codage épars sur MNIST. Chaque image est une colonne apprise de $W$

Lorsqu’un système de codage épars est entraîné sur des images naturelles, les caractéristiques apprises sont les filtres de Gabor, qui sont des bords orientés. Ces caractéristiques ressemblent aux caractéristiques apprises dans les premières parties des systèmes visuels des animaux.

Codage convolutif épars

Supposons que nous ayons une image et les cartes de caractéristiques ($z_1, z_2, \cdots, z_n$) de l’image. Nous pouvons faire une convolution ($*$) de chacune des cartes de caractéristiques avec le noyau $K_i$. La reconstruction peut être alors simplement calculée comme :

Cela est différent du codage épars original où la reconstruction est faite sous la forme $Y=\sum_{i}W_iZ_i$. Dans le codage épars de base, nous avons une somme pondérée de colonnes où les poids sont des coefficients de $Z_i$. Dans le codage convolutif épars, il s’agit toujours d’une opération linéaire, mais la matrice du dictionnaire est maintenant un ensemble de cartes de caractéristiques et nous effectuons une convolution de chacune d’elles avec chaque noyau et nous additionnons les résultats.

Auto-encodeur convolutif épars sur des images naturelles

Figure 6 : Filtres et fonctions de base obtenus. Décodeur convolutionnel linéaire

Les filtres de l’encodeur et du décodeur se ressemblent beaucoup. L’encodeur est simplement une convolution suivie d’une non-linéarité, puis une couche diagonale pour changer l’échelle. Ensuite, il y a de l’éparsité sur la contrainte du code. Le décodeur n’est qu’un décodeur linéaire convolutif et la reconstruction est ici l’erreur quadratique.

Donc, si nous imposons qu’il n’y ait qu’un seul filtre, alors il s’agit juste d’un filtre de type center surround. Avec deux filtres, nous pouvons obtenir des filtres de forme étrange. Avec quatre filtres, nous obtenons des bords orientés (horizontaux et verticaux) et 2 polarités pour chacun des filtres. Avec huit filtres, nous pouvons obtenir des bords orientés à 8 orientations différentes. Avec 16 filtres, nous obtenons plus d’orientation ainsi que les center surround. En augmentant les filtres, on obtient des filtres plus variés, c’est-à-dire en plus des détecteurs de bords, on obtient également des détecteurs de réseaux de différentes orientations, des center surround, etc.

Ce phénomène semble intéressant car il est similaire à ce que nous observons dans le cortex visuel. C’est donc une indication que nous pouvons apprendre de très bonnes caractéristiques d’une manière totalement non supervisée.

Par ailleurs, si nous prenons ces caractéristiques et les connectons à un réseau convolutif, puis que nous les entraînons à une tâche quelconque, nous n’obtenons pas nécessairement de meilleurs résultats qu’un réseau d’images entraîner à partir de zéro. Cependant, dans certains cas, cela peut contribuer à améliorer les performances. Par exemple, dans les cas où le nombre d’échantillons n’est pas assez important ou s’il y a peu de catégories, en entraînant de manière purement supervisée, nous obtenons des caractéristiques dégénérées.

Figure 7 : Codage convolutif épars sur une image en couleur

La figure ci-dessus est un autre exemple sur les images en couleur. Le noyau de décodage (sur le côté droit) est de taille 9 par 9. Ce noyau est appliqué par convolution sur l’ensemble de l’image. L’image de gauche est constituée des codes épars de l’encodeur. Le vecteur $Z$ est un espace très épars où il n’y a que peu de composantes blanches ou noires (non grises).

Auto-encodeurs variationnels

Les auto-encodeurs variationnels ont une architecture similaire à celle des EBMs à variable latente régularisée, à l’exception de l’éparsité. Au contraire, le contenu informationnel du code est limité en le rendant bruyant.

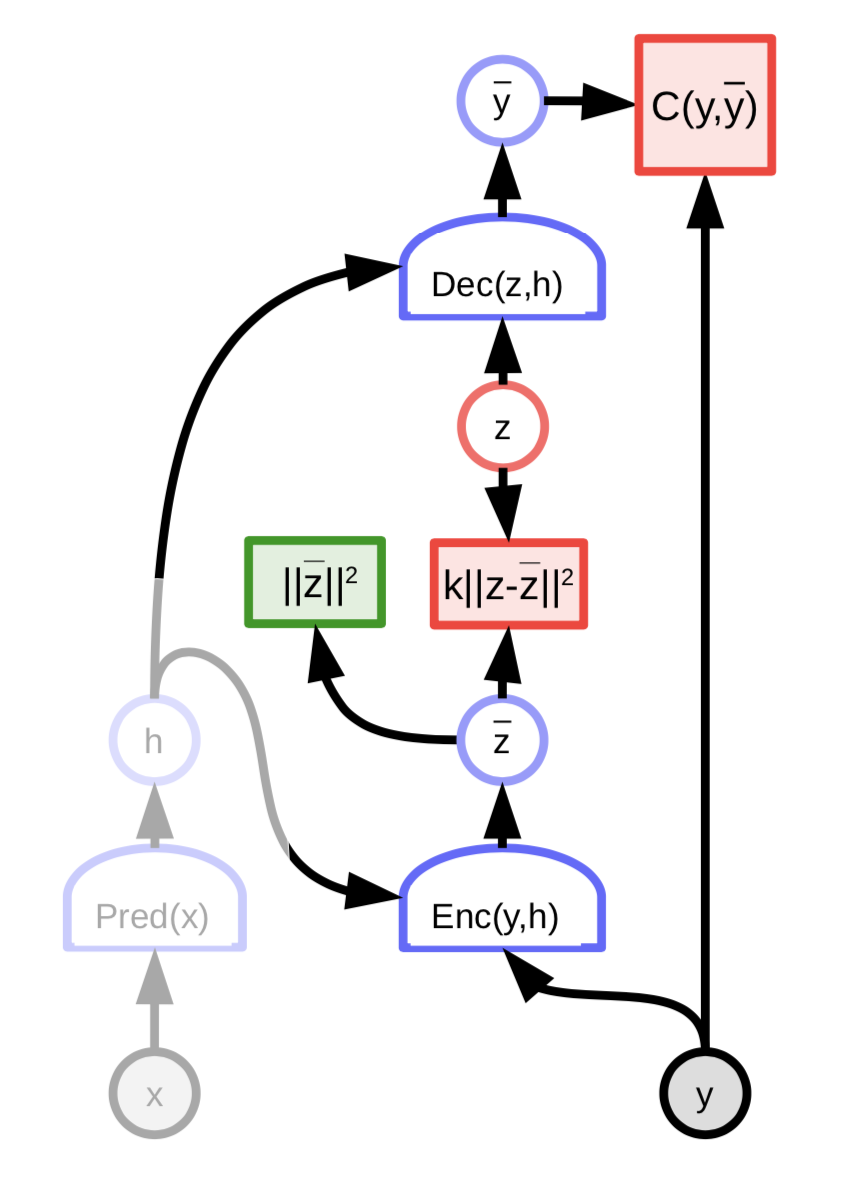
Figure 8 : Architecture de l'auto-encodeur variationnel

La variable latente $z$ n’est pas calculée en minimisant la fonction énergie par rapport à $z$. Au lieu de cela, la fonction énergie est considérée comme un échantillonnage aléatoire de $z$ selon une distribution dont le logarithme est le coût qui la relie à ${\overline z}$. La distribution est une gaussienne avec une moyenne de ${\overline z}$ et cela se traduit par l’ajout d’un bruit gaussien à ${\overline z}$.

Les vecteurs de code avec ajout de bruit gaussien peuvent être visualisés sous forme de boules floues, comme le montre la figure 9(a).

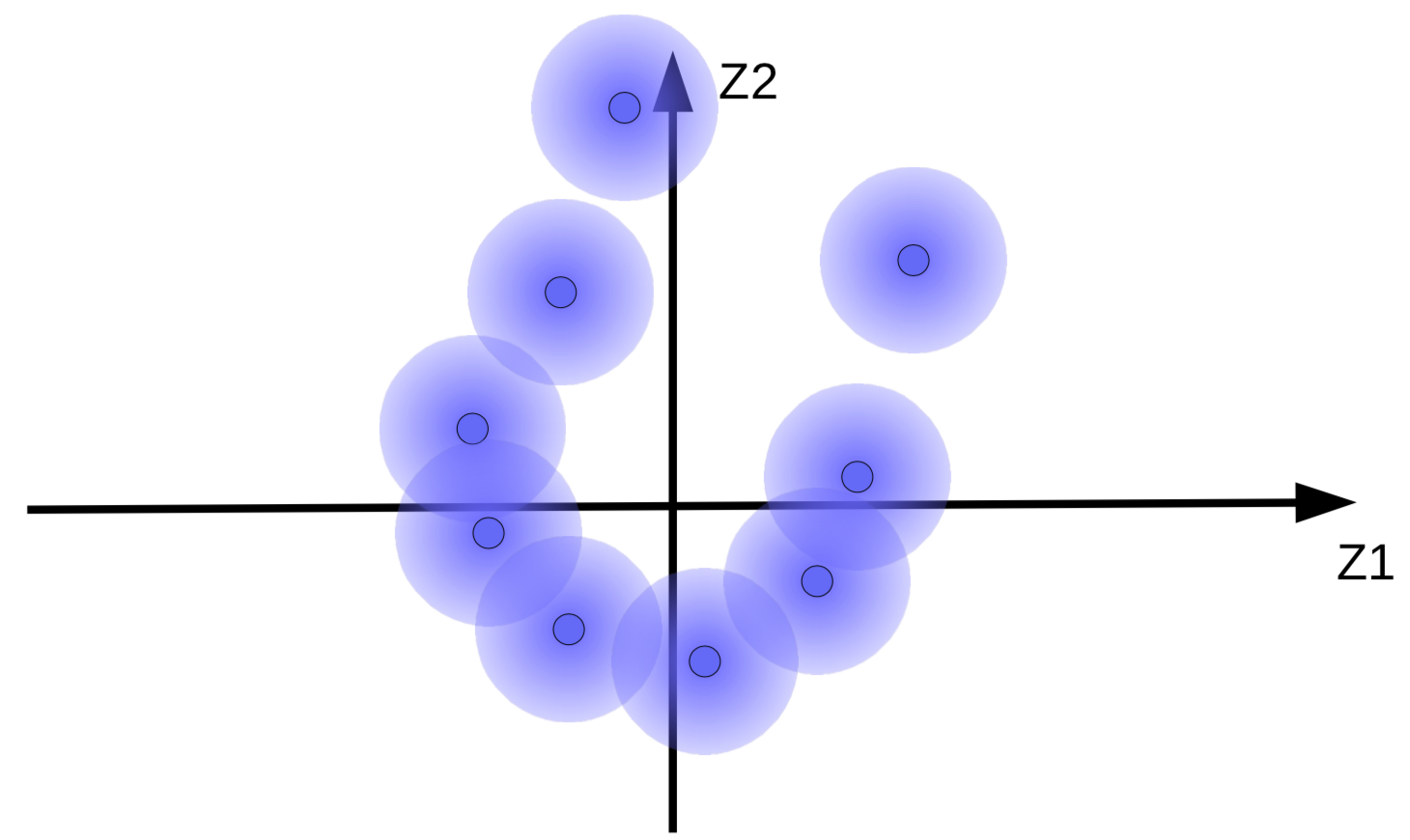(a) Ensemble original de « boules floues »

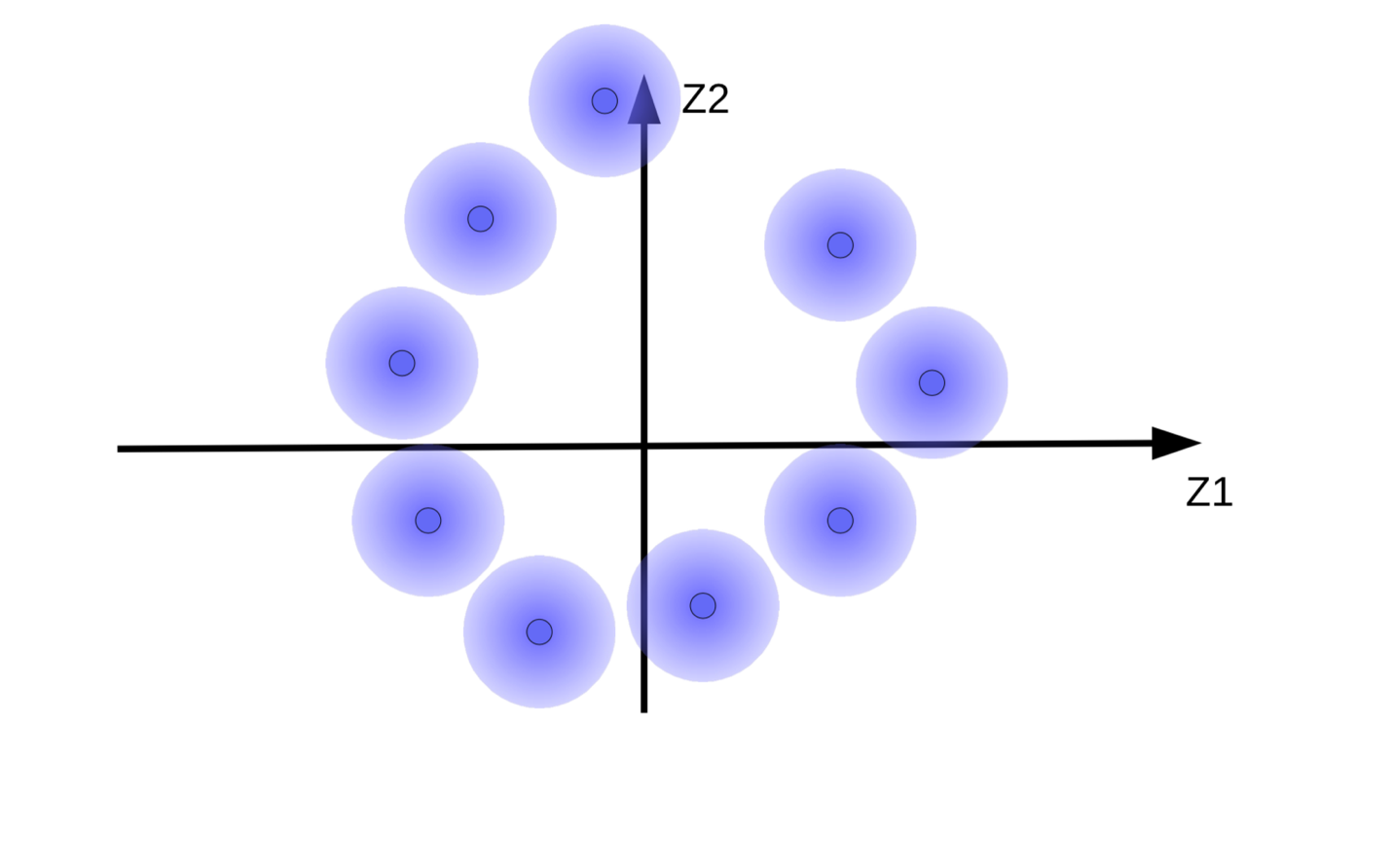(b) Mouvement de « boules floues » dû à la minimisation de l'énergie sans régularisation

Le système essaie de rendre les vecteurs de code ${\overline z}$ aussi grands que possible afin que l’effet de $z$ (bruit) soit aussi petit que possible. Cela a pour résultat que les « boules floues » s’éloignent de l’origine comme le montre la figure 9(b). Une autre raison pour laquelle le système tente de rendre les vecteurs de code plus grands est d’éviter le chevauchement des « boules floues », qui entraîne une confusion du décodeur entre les différents échantillons lors de la reconstruction.
Mais nous voulons que les boules floues se regroupent autour d’une variété de données, s’il y en a une. Ainsi, les vecteurs de code sont régularisés pour avoir une moyenne et une variance proches de 0. Pour ce faire, nous les relions à l’origine par un ressort comme le montre la figure 10.

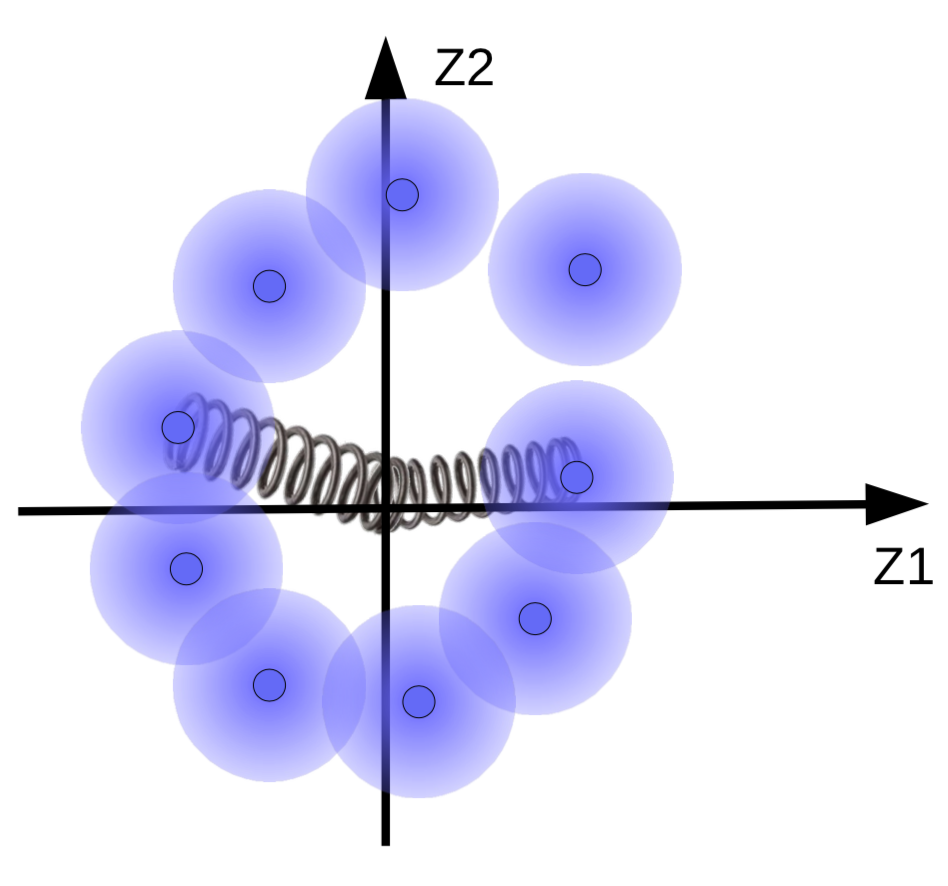
Figure 10 : Effets de la régularisation visualisés avec des ressorts

La force du ressort détermine la proximité des « boules floues » par rapport à l’origine. Si le ressort est trop faible, les boules s’éloignent de l’origine. Et si le ressort est trop fort, alors elles s’effondrent à l’origine, ce qui entraîne une valeur d’énergie élevée. Pour éviter cela, le système ne laisse les sphères se chevaucher que si les échantillons correspondants sont similaires. Il est également possible d’adapter la taille des boules floues. Ceci est limité par une fonction de pénalité (KL Divergence) qui tente de rendre la variance proche de 1 afin que la taille de la boule ne soit ni trop grande ni trop petite pour qu’elle s’effondre.