Apprentissage autosupervisé, détails des EBMs et exemples

Apprentissage autosupervisé

L’apprentissage autosupervisé (SSL pour Self-Supervised Learning) englobe à la fois l’apprentissage supervisé et non supervisé. L’objectif du SSL est d’apprendre une bonne représentation de l’entrée afin qu’elle puisse ensuite être utilisée pour des tâches supervisées. En SSL, le modèle est entraîné pour prédire une partie des données en fonction d’autres parties des données. Par exemple, BERT a été entraîné en combinant le SSL et l’auto-encodeur débruiteur. Ce modèle a montré des résultats de pointe en traitement du langage naturel (NLP pour Natural Language Processing).

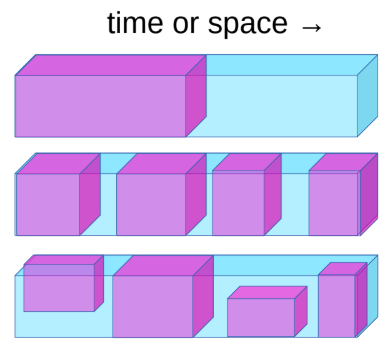
Figure 1 : Apprentissage autosupervisé

La tâche d’apprentissage autosupervisé peut être définie comme suit :

• prévoir l’avenir à partir du passé
• prédire le masqué à partir du visible
• prévoir les parties occultées à partir de toutes les parties disponibles

Par exemple, si un système est entraîné à prédire l’image suivante d’une vidéo, lorsque la caméra est déplacée, le système apprend implicitement la profondeur et la parallaxe. Cela oblige le système à apprendre que les objets occultés de sa vision ne disparaissent pas mais continuent d’exister. De même pour la distinction entre les objets animés, inanimés et l’arrière-plan. Le système peut également finir par apprendre la physique intuitive comme la gravité.

Les systèmes de NLP de pointe sont pré-entraînés via des réseaux neuronaux géants et du SSL. Nous supprimons certains mots d’une phrase et faisons en sorte que le système prédise les mots manquants. Cette méthode (BERT) a été couronnée de succès. Des idées similaires ont également été expérimentées dans le domaine de la vision par ordinateur. Comme le montre l’image ci-dessous, il est possible de prendre une image et en supprimer une partie, puis entraîner le modèle à prédire la partie manquante.

Figure 2 : Résultats en vision par ordinateur

Bien que les modèles puissent combler l’espace manquant, ils n’ont pas connu le même succès que les applications en NLP. Si nous prenons les représentations internes générées par ces modèles et les donnons en entrée d’un système de vision par ordinateur, celui-ci est incapable de battre un modèle qui a été pré-entraîné de manière supervisée sur ImageNet. La différence de succès est qu’en NLP les mots sont discrets alors qu’en vision les images sont continues. Dans le domaine discret, nous savons comment représenter l’incertitude, nous pouvons utiliser un grand softmax sur les sorties possibles alors que ce n’est pas le cas dans le domaine continu.

Un système intelligent doit être capable de prédire les résultats de sa propre action sur l’environnement et de prendre lui-même des décisions intelligentes. Comme le monde n’est pas complètement déterministe et qu’il n’y a pas assez de puissance de calcul dans une machine/un cerveau humain pour prendre en compte toutes les possibilités, nous devons apprendre aux systèmes d’IA à prédire en présence d’incertitude dans les espaces en grandes dimensions. Les EBMs peuvent être extrêmement utiles à cet effet.

Un réseau neuronal entraîné à l’utilisation des moindres carrés pour prédire la prochaine image d’une vidéo produira des images floues parce que le modèle ne peut pas prédire exactement l’avenir. Pour réduire la perte, il apprend donc à faire la moyenne de toutes les possibilités de la prochaine image à partir des données d’entraînement.

Les EMBs à variable latente comme solution pour faire des prédictions d’une image suivante

Contrairement à la régression linéaire, les EMBs à variable latente prennent ce que nous savons du monde ainsi qu’une variable latente qui nous donne des informations sur ce qui s’est passé dans la réalité. Une combinaison de ces deux éléments d’information peut être utilisée pour faire une prédiction qui sera proche de ce qui se passe réellement.

Ces modèles peuvent être considérés comme des systèmes qui évaluent la compatibilité entre l’entrée $x$ et la sortie réelle $y$ en fonction de la prédiction utilisant la variable latente qui minimise l’énergie du système. Nous observons l’entrée $x$, produisons des prédictions possibles $\bar{y}$ pour différentes combinaisons ($x$,$z$) et choisissons celle qui minimise l’énergie, l’erreur de prédiction, du système.

En fonction de la variable latente que nous tirons, nous pouvons nous retrouver avec toutes les prédictions possibles. La variable latente peut être considérée comme une information importante sur la sortie $y$ qui n’est pas présente dans l’entrée $x$.

La fonction d’énergie à valeur scalaire peut prendre deux versions :

1. conditionnelle : $F(x, y)$ mesure la compatibilité entre $x$ et $y$
2. inconditionnel : $F(y)$ mesure la compatibilité entre les composantes de $y$

Entraîner un EBM

Il existe deux classes de modèles d’apprentissage pour entraîner un EMB à paramétrer $F(x, y)$.

1. Les méthodes contrastives : on pousse vers le bas sur $F(x[i], y[i])$ et on pousse vers le haut sur d’autres points $F(x[i], y’)$
2. Les méthodes architecturales : on construit $F(x, y)$ de manière à limiter ou à minimiser le volume des régions à faible énergie par la régularisation

Il existe sept stratégies pour façonner la fonction d’énergie. Les méthodes contrastives diffèrent dans la manière de choisir les points à pousser vers le haut. Les méthodes architecturales diffèrent dans la façon dont elles limitent la capacité d’information du code.

Un exemple de la méthode contrastive est l’apprentissage par maximum de vraisemblance. L’énergie peut être interprétée comme une densité logarithmique négative non normalisée. La distribution de Gibbs nous donne la vraisemblance de $y$ pour $x$. Elle peut être formulée comme suit :

Le maximum de vraisemblance essaie de rendre le numérateur grand et le dénominateur petit pour maximiser la probabilité. Cela équivaut à minimiser $-\log(P(Y \mid W))$ qui est donné ci-dessous :

Le gradient de la perte de la vraisemblance logarithmique négative pour un échantillon Y est le suivant :

Dans le gradient ci-dessus, le premier terme du gradient au point de données $Y$ et le second terme du gradient nous donne la valeur attendue du gradient de l’énergie sur l’ensemble des $Y$. Ainsi, lorsque nous effectuons la descente de gradient, le premier terme tente de réduire l’énergie donnée au point de données $Y$ et le second terme tente d’augmenter l’énergie donnée à tous les autres $Y$.

Le gradient de la fonction d’énergie est généralement très complexe et par conséquent le calcul, l’estimation ou l’approximation de l’intégrale est un cas très intéressant car il est insoluble dans la plupart des cas.

EMB à variable latente

Le principal avantage des modèles à variables latentes est qu’ils permettent des prévisions multiples grâce à la variable latente. Comme $z$ varie sur un ensemble, $y$ varie sur la multiplicité des prédictions possibles. En voici quelques exemples :

1. K-means
2. Modélisation
3. GLO

Il peut y en avoir de deux types :

1. Modèles conditionnels où $y$ dépend de $x$ :
   1. \[F(x,y) = \text{min}_{z} E(x,y,z)\]
   2. \[F_\beta(x,y) = -\frac{1}{\beta}\log\int_z e^{-\beta E(x,y,z)}\]
2. Modèles inconditionnels qui ont une fonction d’énergie à valeur scalaire, $F(y)$ qui mesure la compatibilité entre les composantes de $y$ :
   1. \[F(y) = \text{min}_{z} E(y,z)\]
   2. \[F_\beta(y) = -\frac{1}{\beta}\log\int_z e^{-\beta E(y,z)}\]

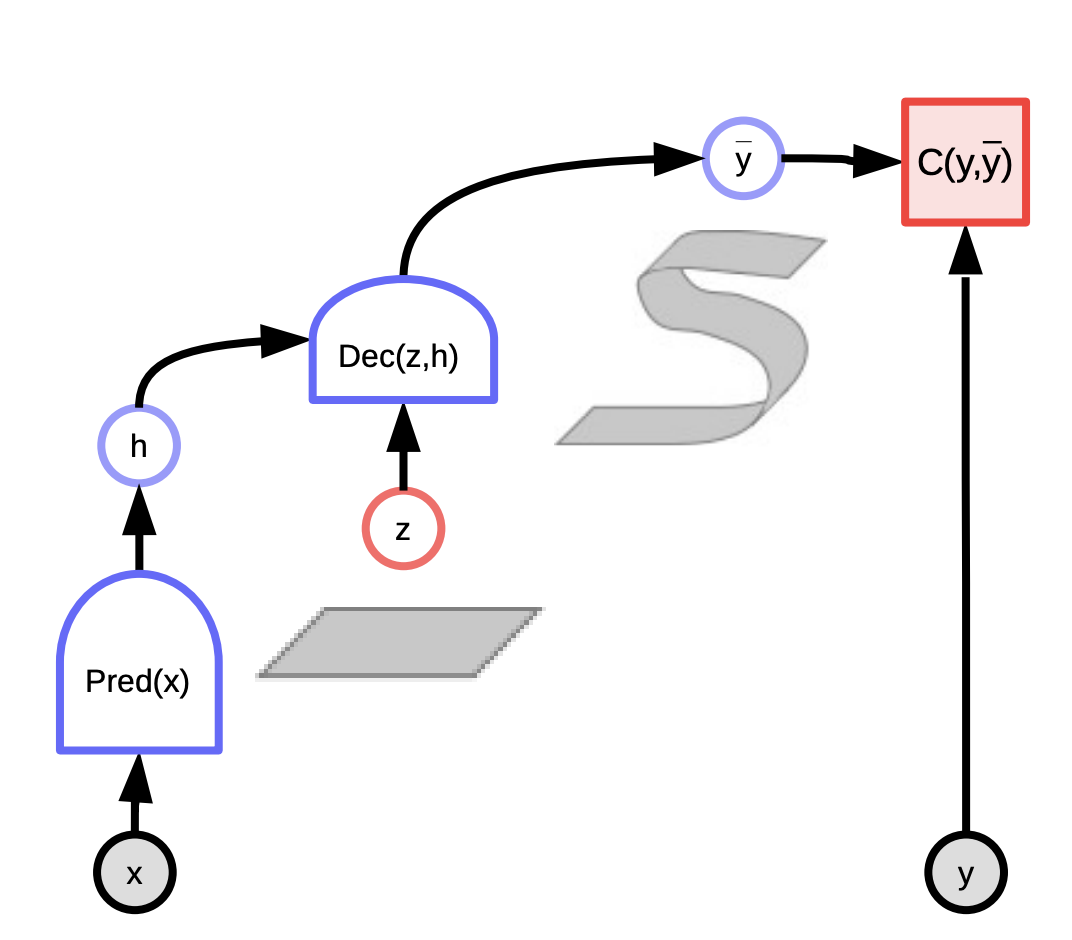
Figure 3 : EBM à variable latente

Exemple d’EMB à variable latente : les $K$-means

Les $K$-means sont un algorithme de clustering simple qui peut également être considéré comme un modèle à base d’énergie dont nous essayons de modéliser la distribution sur $y$. La fonction d’énergie est $E(y,z) = \Vert y-Wz \Vert^2$ où $z$ est un vecteur one-hot.

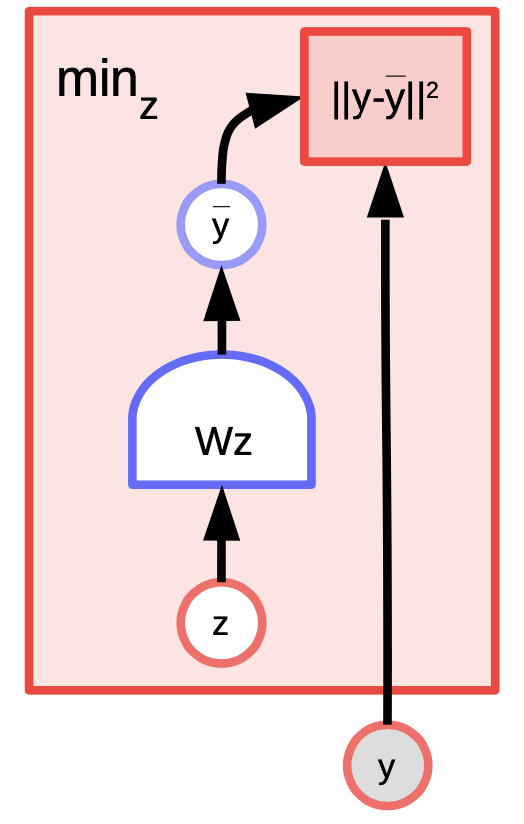
Figure 4 : Exemple des K-means

Avec une valeur de $y$ et $k$, nous pouvons faire une inférence en déterminant laquelle des colonnes possibles de $k$ de $W$ minimise l’erreur de reconstruction ou la fonction d’énergie. Pour entraîner l’algorithme, nous pouvons adopter une approche où nous pouvons trouver $z$ pour choisir la colonne de $W$ la plus proche de $y$ et ensuite essayer de nous rapprocher encore plus en prenant un pas de gradient et en répétant le processus. Cependant, la descente de gradient coordonné fonctionne en fait mieux et plus rapidement.

Dans le graphique ci-dessous, nous pouvons voir les points de données le long de la spirale rose. Les taches noires entourant cette ligne correspondent à des puits quadratiques autour de chacun des prototypes de $W$.

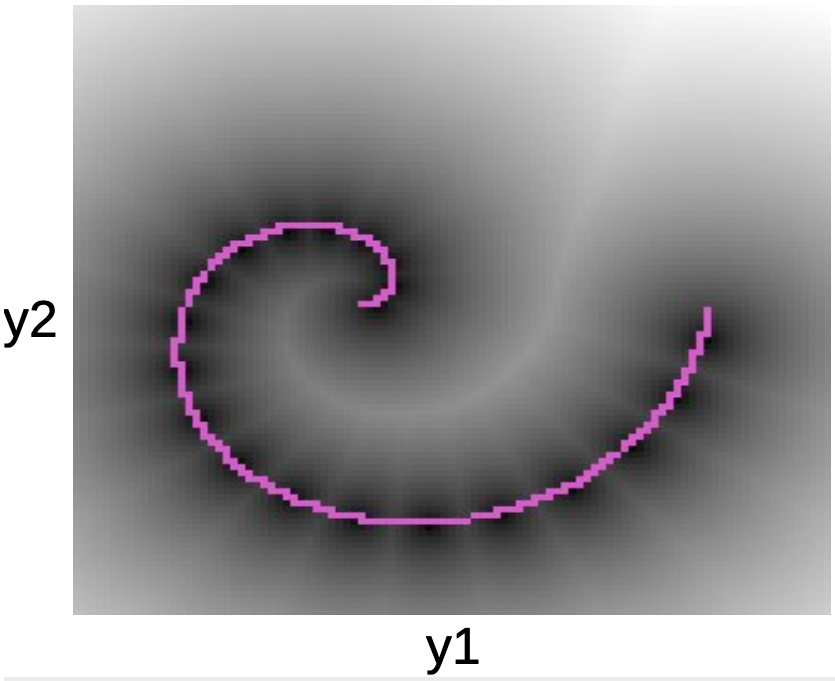
Figure 5 : Graphique de la spirale

Une fois que nous avons appris la fonction d’énergie, nous pouvons commencer à aborder des questions comme :

1. Étant donné un point $y_1$, pouvons-nous prédire $y_2$ ?
2. Étant donné $y$, pouvons-nous trouver le point le plus proche sur la variété des données ?

Les $K$-means appartiennent aux méthodes architecturales (par opposition aux méthodes contrastives). Par conséquent, nous n’augmentons l’énergie nulle part. Tout ce que nous faisons, c’est de la faire baisser dans certaines régions. Un inconvénient est qu’une fois que la valeur de $k$ a été décidée, il ne peut y avoir que des points $k$ qui ont une énergie de $0$. Tous les autres points auront une énergie plus élevée qui croîtra de façon quadratique à mesure que nous nous en éloignerons.

Les méthodes contrastives

Selon Yann, tout le monde utilisera un jour des méthodes architecturales, mais pour l’instant, ce sont les méthodes contrastives qui fonctionnent pour les images. Considérons la figure ci-dessous qui nous montre quelques points de données et les contours de la surface énergétique. Idéalement, nous voulons que la surface énergétique ait l’énergie la plus faible sur la variété des données. Par conséquent, nous aimerions réduire l’énergie (c’est-à-dire la valeur de $F(x,y)$) autour de l’exemple d’entraînement, mais cela peut ne pas suffire. C’est pourquoi nous l’augmentons également pour les $y$ dans la région qui devrait avoir une énergie élevée mais qui a une énergie faible.

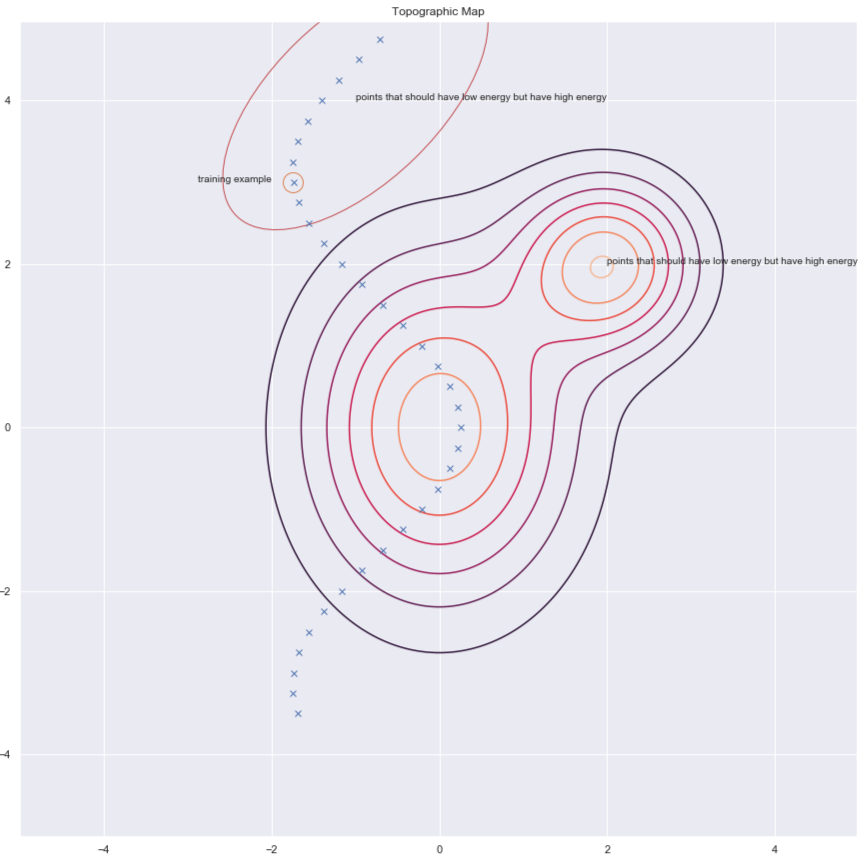
Figure 6 : Méthodes contrastives

Il y a plusieurs façons de trouver les candidats pour lesquels nous voulons collecter de l’énergie. En voici quelques exemples :

1. L’auto-encodeur débruiteur (DAE)
2. La divergence contrastive
3. Monte Carlo
4. Les chaînes de Markov par Monte Carlo
5. Monte Carlo Hamiltonien

Aborderons brièvement la question des DAEs et de la divergence contrastive.

Auto-encodeur débruiteur (DAE)

Une façon de trouver des $y$ pour augmenter l’énergie nécessaire est de perturber aléatoirement l’exemple d’entraînement comme le montrent les flèches vertes dans le graphique ci-dessous :

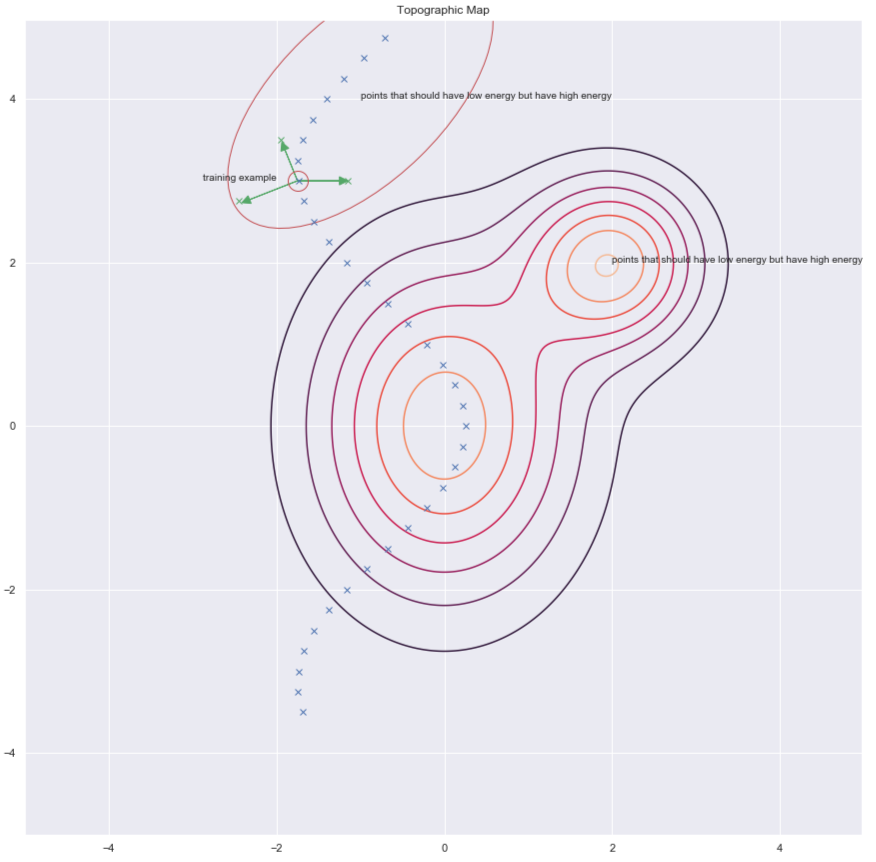
Figure 7 : Carte topographique

Une fois que nous avons un point de données corrompu, nous pouvons pousser l’énergie jusqu’ici. Si nous le faisons suffisamment de fois pour tous les points de données, l’échantillon d’énergie se recroquevillera autour des exemples d’entraînement. Le graphique suivant illustre la façon dont l’entraînement est effectué :

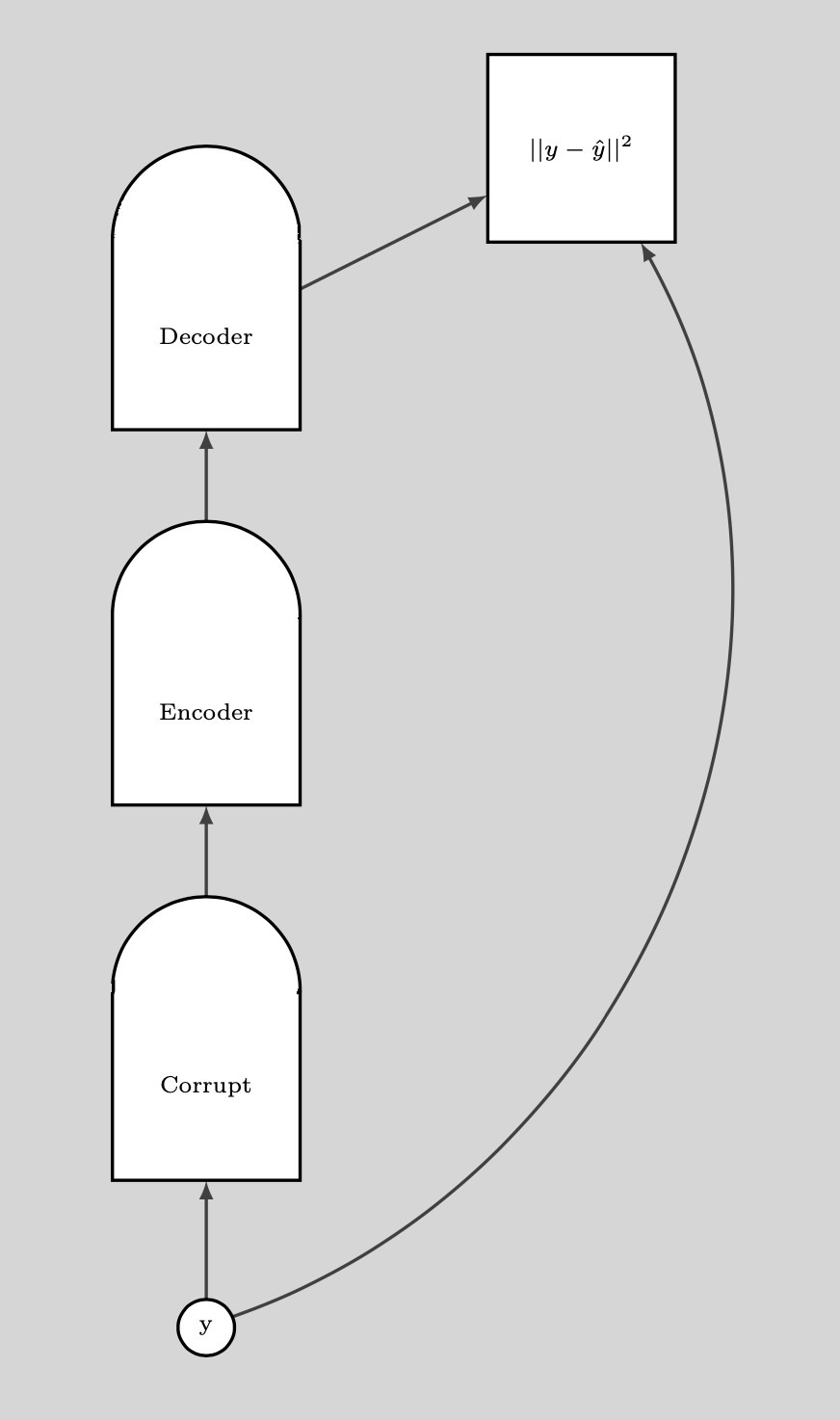
Figure 8 : Entraînement

Étapes de l’entraînement :

1. Prendre un point $y$ et le corrompre
2. Entraîner l’encodeur et le décodeur à reconstruire le point de données original à partir de ce point de données corrompu

Si le DAE est correctement entraîné, l’énergie croît de façon quadratique à mesure que nous nous éloignons de la surface de données.

Le graphique suivant illustre la façon dont nous utilisons le DAE.

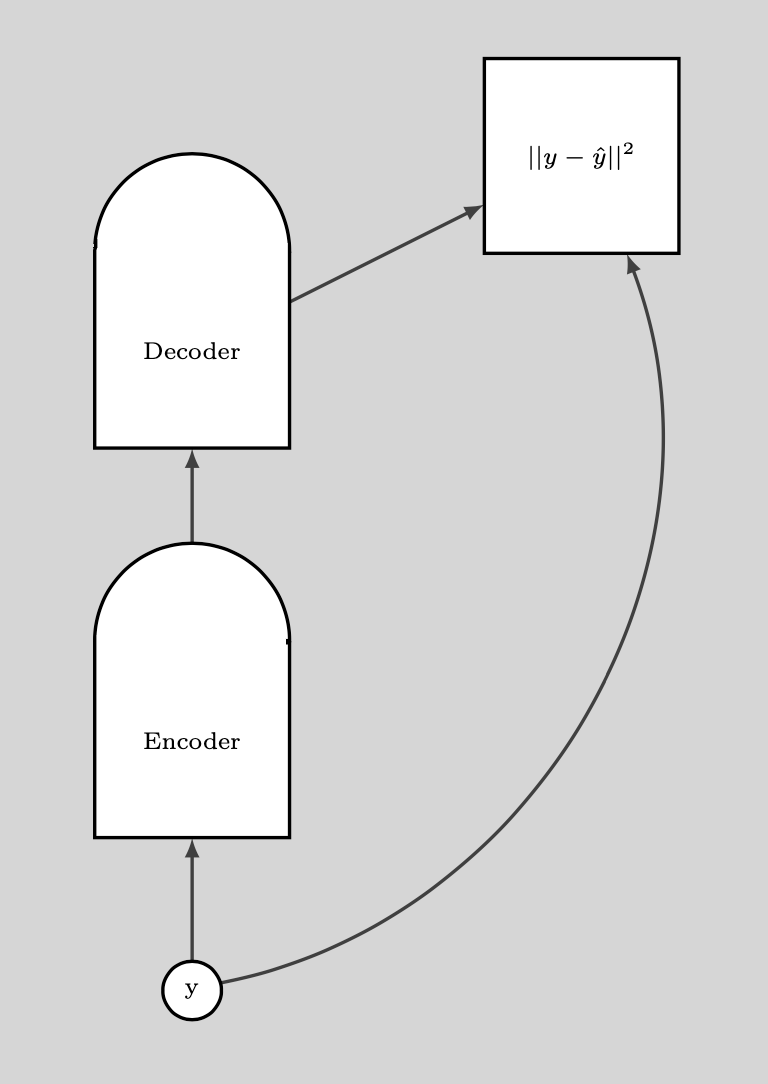
Figure 9 : Utilisation du DAE

BERT

BERT est entraîné de la même manière, sauf que l’espace est discret car nous avons affaire à du texte. La technique de corruption consiste à masquer certains mots et l’étape de reconstruction consiste à essayer de les prédire. C’est pourquoi on appelle aussi cela un auto-encodeur masqué.

Divergence contrastive

La divergence contrastive nous offre une façon plus intelligente de trouver le point $y$ pour lequel nous voulons faire monter l’énergie. Nous pouvons donner un « coup de pied » aléatoire à notre point d’entraînement et ensuite descendre la fonction d’énergie en utilisant la descente de gradient. A la fin de la trajectoire, nous poussons l’énergie vers le haut pour le point où nous atterrissons. Ceci est illustré dans le graphique ci-dessous par la ligne verte.

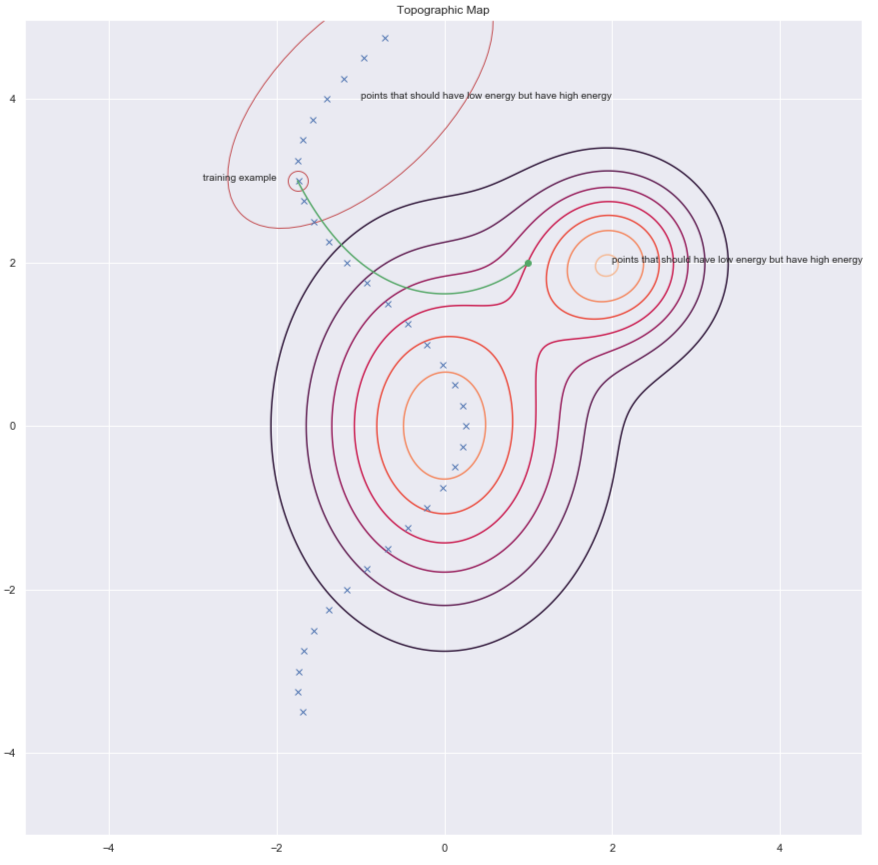
Figure 10 : Divergence contrastive