Réseau convolutif pour graphe I

🎙️ Xavier Bresson

Réseaux convolutifs traditionnels

Les réseaux convolutifs sont des architectures puissantes permettant de résoudre des problèmes d’apprentissage en grandes dimensions.

Qu’est-ce que la malédiction de la dimensionnalité ?

Considérons une image de $1024 \times 1024$ pixels. Cette image peut être considérée comme un point dans l’espace de $1 000 000$ de dimensions. L’utilisation de 10 échantillons par dimension génère ${10}^{1 000 000}$ images, ce qui est extrêmement élevé. Les réseaux convolutifs sont extrêmement puissants pour extraire la meilleure représentation des données d’images en grandes dimensions, comme celle donnée dans l’exemple.

• dim(image) = $1024 \times 1024$ = ${10}^{6}$
• Pour $N = 10$ échantillons/dim => ${10}^{1 000 000}$ points

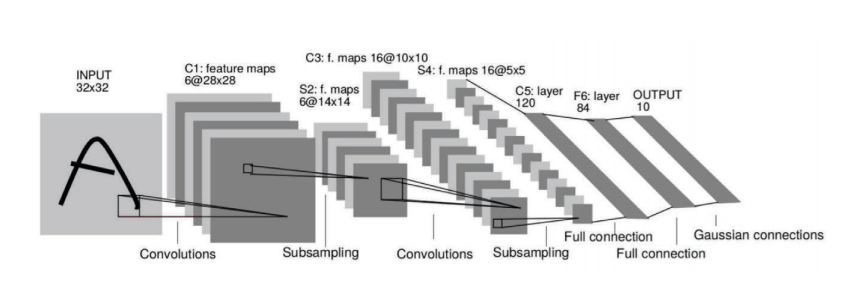
Figure 1 : Les réseaux convolutifs extraient la représentation des données en grandes dimensions des images

Principales hypothèses sur les ConvNets :

1. Les données (images, vidéos, discours) sont compositionnelles.

Elles sont formées de motifs qui sont :

• Locaux : un neurone du réseau neuronal n’est connecté qu’aux couches adjacentes, mais pas à toutes les couches du réseau. C’est ce que nous appelons l’hypothèse du champ de réception local.
• Stationnaires : nous avons des motifs qui sont similaires et qui sont partagés dans tout notre domaine d’image. Par exemple, le drap de lit jaune dans l’image du milieu de la figure 2.
• Hiérarchiques : les caractéristiques de bas niveau seront combinées pour former des caractéristiques de niveau moyen. Par la suite, ces éléments de niveau moyen seront combinés pour former des éléments de niveau supérieur.

Figure 2 : Les données sont compositionnelles

2. Les ConvNets tirent parti de la compositionnalité de la structure.

Ils extraient les caractéristiques de composition et les transmettent au classifieur, au recommandeur, etc.

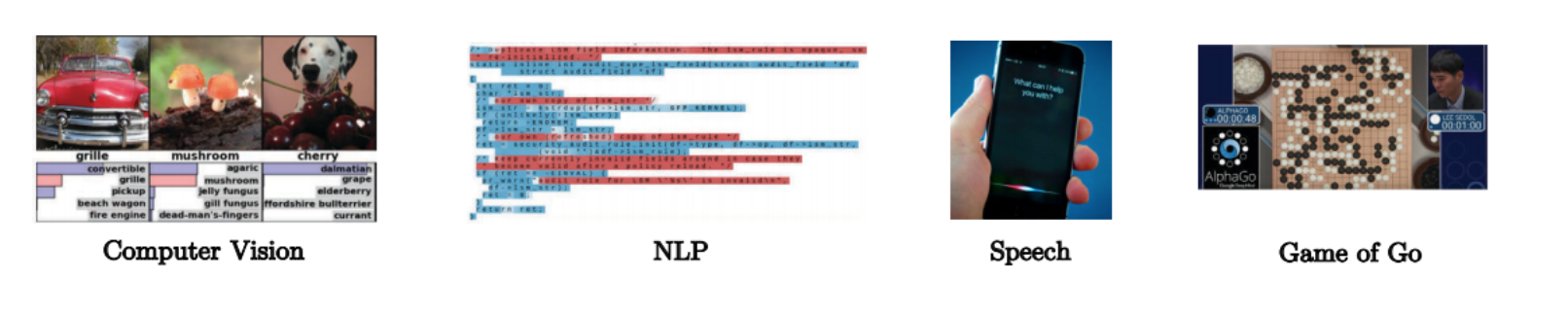
Figure 3 : Les ConvNets tirent parti de la compositionnalité de la structure

Domaine du graphe

Domaine des données

• Les images, volumes, vidéos se situent sur des domaines euclidiens 2D, 3D, 2D+1 (grilles). Chaque pixel est représenté par un vecteur de valeurs rouge, vert et bleu.

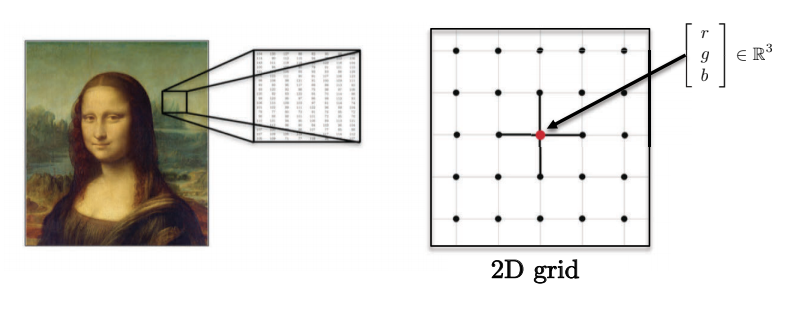
Figure 4 : Les images ont de multiples dimensions

• Les phrases, les mots, la parole se trouvent sur le domaine euclidien 1D. Par exemple, chaque caractère peut être représenté par un entier.

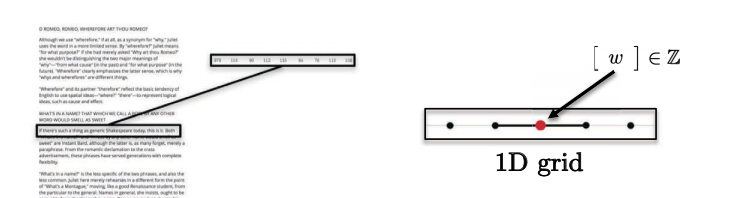
Figure 5 : Les séquences ont une seule dimension

• Ces domaines ont de fortes structures spatiales régulières, ce qui permet à toutes les opérations des réseaux convolutifs d’être rapides et mathématiquement bien définies.

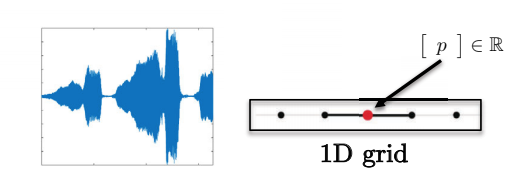
Figure 6 : Les données vocales ont une grille 1D

Domaine du graphe

Exemples de domaine du graphe

Envisageons un réseau social. Le réseau social est mieux capturé par une représentation sous forme de graphe car la connexion par paire entre deux utilisateurs ne forme pas une grille. Les nœuds du graphe représentent les utilisateurs, tandis que les arêtes entre deux nœuds représentent la connexion entre deux utilisateurs. Chaque utilisateur dispose d’une matrice de caractéristiques tridimensionnelles contenant des messages, des images et des vidéos.

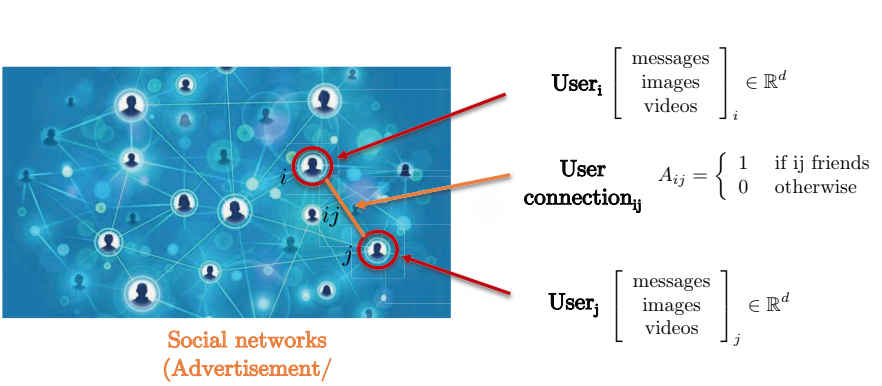
Figure 7 : Représentation d'un réseau social sous la forme d'un graphe

Le lien entre la structure et la fonction du cerveau pour prédire les maladies génétiques neurales offre un exemple de motivation à prendre en considération. Comme on peut le voir ci-dessous, le cerveau est composé de plusieurs régions d’intérêt (ROIs pour Regions of Interest). Ces ROIs ne sont connectées que localement à certaines régions d’intérêt environnantes. La matrice d’adjacence représente le degré de force entre les différentes régions d’intérêt.

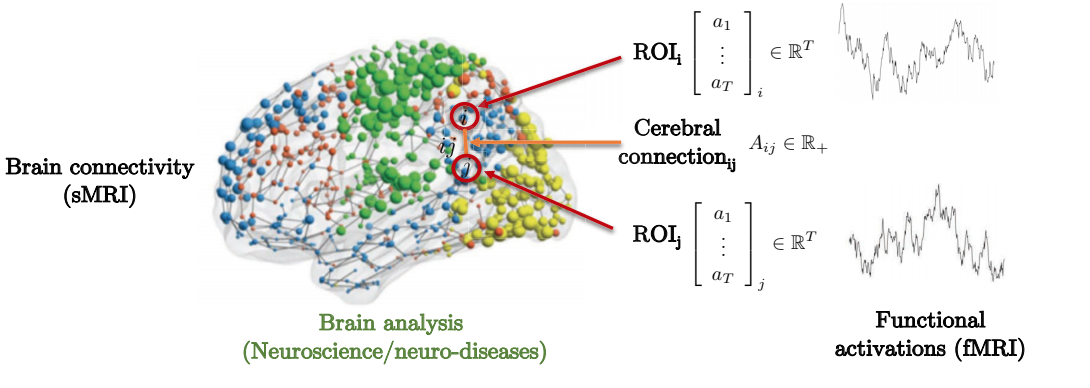
Figure 8 : Représentation de la connectivité cérébrale sous la forme d'un graphe

La chimie quantique offre également une représentation intéressante du domaine graphique. Chaque atome est représenté par un nœud dans le graphe et est relié aux autres atomes par des liaisons utilisant des arêtes. Chacun de ces molécules/atomes présente des caractéristiques différentes, telles que la charge associée, le type de liaison, etc.

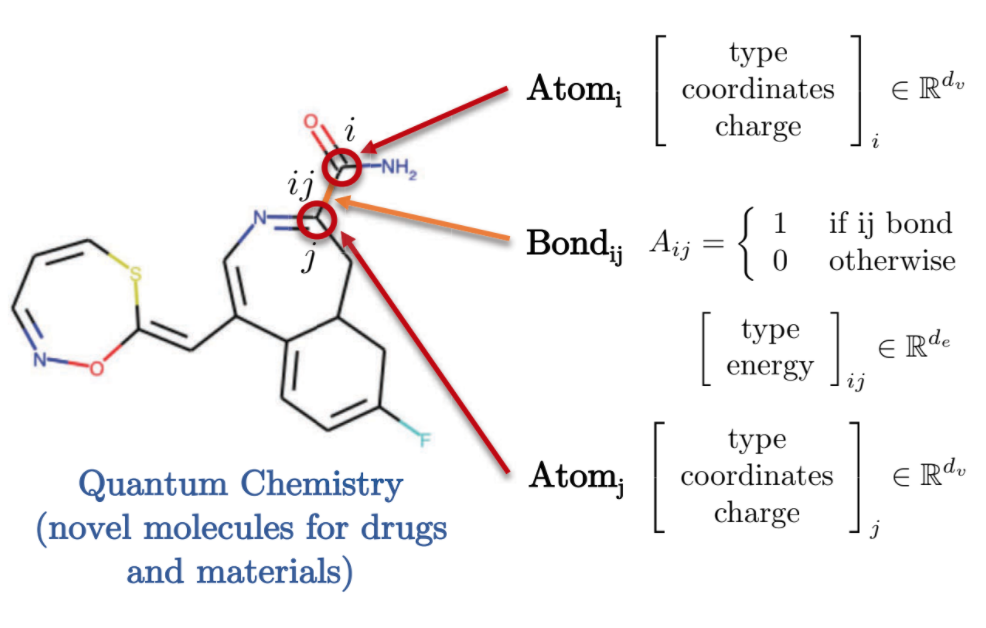
Figure 9 : Représentation de la chimie quantique sous la forme d'un graphe

Définition et caractéristiques des graphes

• Le graphe G est défini par :
  • des sommets V (V pour vertices en anglais)
  • des arêtes E (E pour edges en anglais)
  • une matrice d’adjacence A
• Les caractéristiques d’un graphe :
  • caractéristiques au niveau d’un nœud : $h_{i}$, $h_{j}$ (ex : un atome)
  • caractéristiques au niveau d’un arête : $e_{ij}$ (ex : une liaison entre atome)
  • caractéristiques au niveau du graphe : g (ex : une molécule)

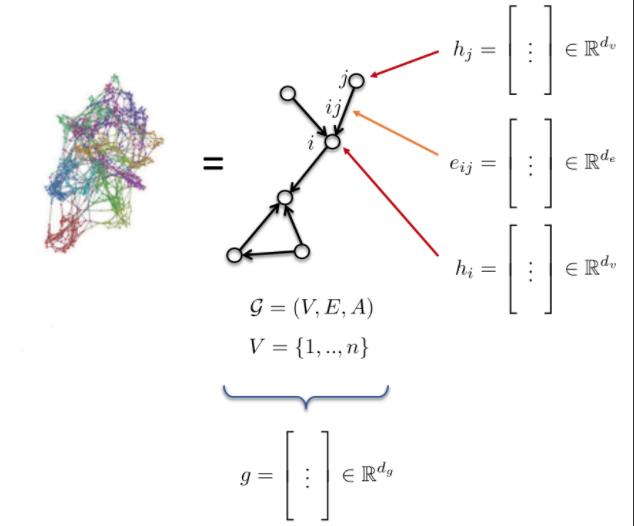
Figure 10 : Graphe

Convolution des ConvNets traditionnels

Convolution

Nous définissons abstraitement la convolution comme :

\(h^{\ell+l} = w^\ell * h^\ell,\) où $h^{\ell+1}$ est $n_1\times n_2\times d$-dimensionnel, $w^\ell$ est $3\times 3\times d$-dimensionnel, et $h^\ell$ est $n_1\times n_2\times d$-dimensionnel. Par exemple, $n_1$ et $n_2$ pourraient être le nombre de pixels dans les directions $x$ et $y$ d’une image, respectivement, et $d$ la dimensionnalité de chaque pixel (par exemple, $3$ pour une image en couleur). Ainsi, $h^{\ell+1}$ est une caractéristique au niveau de la $(\ell+1)$-ème couche cachée obtenue en appliquant la convolution $w^\ell$ à une caractéristique au niveau de la $\ell$-ème couche. Habituellement, le noyau est petit pour représenter un champ de réception local ($3\times 3$ ou $5\times 5$ par exemple). Note : nous utilisons un rembourrage pour nous assurer que les dimensions de $h^{\ell+1}$ sont les mêmes que celles de $h^\ell$.

Par exemple, dans cette image, le noyau peut être utilisé pour reconnaître les lignes.

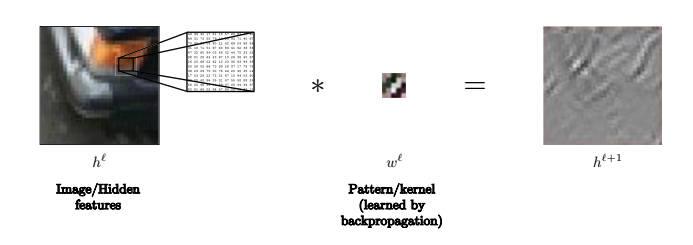
Figure 11 : Le noyau peut être utilisé pour reconnaître les lignes dans les images

Comment définir la convolution ?

Plus précisément, la convolution est définie comme suit :

\[h_i^{\ell+1} = w^\ell * h_i^\ell\] \[= \sum_{j\in\Omega}\langle w_j^\ell, h_{i-j}^\ell\rangle\] \[= \sum_{j\in\mathcal{N}_i} \langle w_j^\ell, h_{ij}^\ell\rangle\] \[=\sum_{j\in\mathcal{N}_i} \langle \Bigg[w_j^\ell\Bigg], \Bigg[h_{ij}\Bigg]\rangle\]

Ce qui précède définit la convolution comme l’appariement de patrons/pochoirs (template matching).

Nous utilisons généralement $h_{i+j}$ au lieu de $h_{i-j}$, car la première ligne est en fait une corrélation, qui ressemble davantage à l’appariement de patrons.

Cependant, peu importe que nous utilisions la première ou la deuxième ligne car notre noyau est simplement retourné et cela n’a pas d’incidence sur l’apprentissage.

Dans la troisième ligne, nous écrivons simplement $h_{i+j}^\ell$ comme $h_{ij}^\ell$.

Le noyau est très petit donc au lieu d’additionner sur toute l’image $\Omega$, comme dans la deuxième ligne, nous additionnons juste sur le voisinage de la cellule $i$, $\mathcal{N}_i$, comme indiqué dans la troisième ligne.

Cela fait que la complexité de la convolution est de $O(n)$ où $n$ est le nombre de pixels de l’image d’entrée.

La convolution est pour chacun des pixels $n$, en additionnant sur les produits internes des vecteurs de dimension $d$ sur des grilles $3\times 3$.

La complexité est donc de $n\cdot 3\cdot 3\cdot d$, ce qui correspond à $O(n)$. De plus le calcul peut être effectué en parallèle avec les GPUs pour chacun des $n$ pixels.

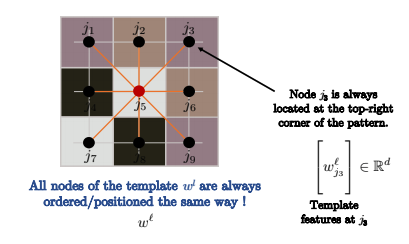
Figure 12 : Les nœuds sont ordonnés de la même manière

Si le graphe sur lequel nous effectuons la convolution est une grille, comme dans la convolution standard sur les images en vision par ordinateur, alors les nœuds sont ordonnés comme dans l’image ci-dessus. Par conséquent, $j_3$ se trouvera toujours dans le coin supérieur droit du graphe.

Ainsi, pour tous les nœuds $i$ dans l’image ci-dessous, comme $i$ et $i’$, l’ordre des nœuds du noyau est toujours le même. Par exemple, nous comparons toujours $j_3$ dans le coin supérieur droit du motif avec le coin supérieur droit du patch de l’image (ce sur quoi nous effectuons une convolution pour le pixel $i$), comme indiqué ci-dessous. Mathématiquement parlant :

\[\langle\Bigg[w_{j_3}^\ell\Bigg], \Bigg[h_{ij_3}^\ell \Bigg]\rangle\]

et

\[\langle\Bigg[w_{j_3}^\ell\Bigg], \Bigg[h_{i'j_3}^\ell \Bigg]\rangle\]

sont toujours pour le coin supérieur droit entre le modèle et les patchs d’image.

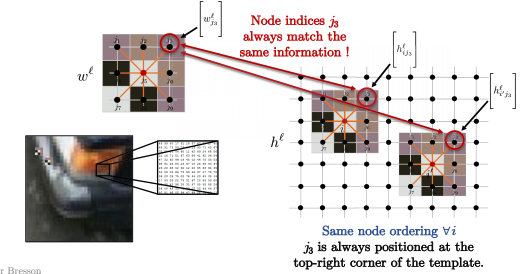
Figure 13 : Les patchs d'image correspondent aux patrons

Pouvons-nous étendre l’appariement de patrons aux graphes ?

Nous avons quelques problèmes :

1. Premièrement, dans un graphe, il n’y a pas d’ordre des nœuds.

Ainsi, dans l’image, le nœud $j_3$ n’a pas de position spécifique, mais juste un index (arbitraire). Donc lorsque nous essayons de faire correspondre les nœuds $i$ et $i’$ dans le graphe ci-dessous, nous ne savons pas si $j_3$ correspond aux mêmes nœuds dans les deux convolutions. Ceci est dû au fait qu’il n’y a pas de notion de coin supérieur droit dans le graphe. Il n’y a pas de notion de haut, bas, gauche droite. Ainsi, l’appariement de patrons n’a en fait aucune signification et nous ne pouvons pas l’utiliser directement comme ci-dessus.

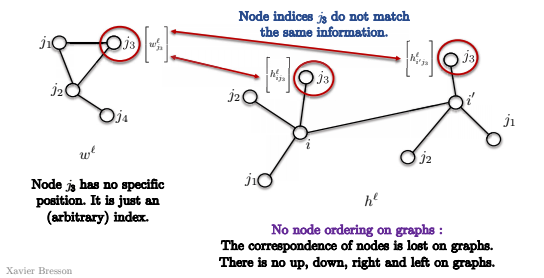
Figure 14 : Pas d'ordre des nœuds dans un graphe

1. Le deuxième problème est que la taille du voisinage peut être différente.

Le modèle $w^\ell$ présenté ci-dessous a 4 nœuds, mais le nœud $i$ a 7 nœuds dans son voisinage. Comment pouvons-nous comparer ces deux choses ?

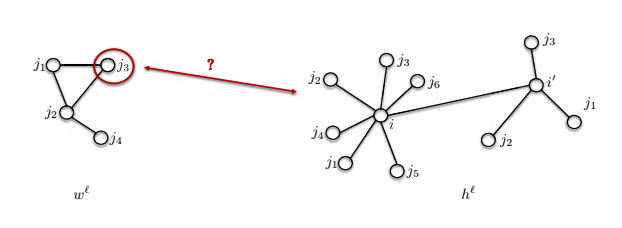
Figure 15 : Différentes tailles de voisinage dans un graphe

Convolution pour un graphe

Nous utilisons maintenant le théorème des convolutions pour définir les convolutions des graphes.

Le théorème des convolutions indique que la transformée de Fourier (FFT) de la convolution de deux fonctions est le produit élément par élément de leurs transformées de Fourier :

\[\mathcal{F}(w*h) = \mathcal{F}(w) \odot \mathcal{F}(h) \implies w * h = \mathcal{F}^{-1}(\mathcal{F}(w)\odot\mathcal{F}(h))\]

En général, la transformée de Fourier a une complexité de $O(n^2)$, mais si le domaine est une grille, alors la complexité peut être réduite à $O(n\log n)$ avec la FFT.

Peut-on étendre le théorème de la convolution aux graphes ?

Cela soulève deux questions :

1. Comment définir les transformées de Fourier pour les graphes ?
2. Comment calculer des convolutions spectrales rapides en temps $O(n)$ pour les noyaux compacts (comme dans l’appariement de patrons) ?

\[w *_{\mathcal{G}} h \stackrel{?}{=} \mathcal{F}^{-1}_{\mathcal{G}}(\mathcal{F}_{\mathcal{G}}(w)\odot\mathcal{F}_{\mathcal{G}}(h))\]

Nous allons utiliser ces deux modèles pour les réseaux de neurones pour graphes. L’appariement de patrons sera utilisé pour les GCNs (ConvNets pour graphe) spatiaux et le théorème de convolution sera utilisé pour les GCNs spectraux.

GCNs spectraux

Comment effectuer une convolution spectrale ?

Étape 1 : Graphe Laplacien

C’est l’opérateur central de la théorie des graphes spectraux.

Définir

\[\begin{aligned} \mathcal{G}=(V, E, A) & \rightarrow \underset{n \times n}{\Delta}=\mathrm{I}-D^{-1 / 2} A D^{-1 / 2} \\ & \quad \text { où } \underset{n \times n} D=\operatorname{diag}\left(\sum_{j \neq i} A_{i j}\right) \end{aligned}\]

$A$ est la matrice d’adjacence et le $\Delta$ est le Laplacien, qui est égal à l’identité moins la matrice d’adjacence normalisée par la matrice $D$. $D$ est une matrice diagonale et chaque élément de la diagonale est le degré du nœud. C’est ce qu’on appelle le Laplacien normalisé ou simplement Laplacien par défaut dans ce contexte.

Le Laplacien est interprété comme la mesure de la finesse du graphe, en d’autres termes, la différence entre la valeur locale $h_i$ et sa valeur moyenne de voisinage de $h_j$’s. $d_i$ sur la formule ci-dessous est le degré du nœud $i$, et $\mathcal{N}_{i}$ est l’ensemble des voisins du nœud $i$.

\[(\Delta h)_{i}=h_{i}-\frac{1}{d_{i}} \sum_{j \in \mathcal{N}_{i}} A_{i j} h_{j}\]

La formule ci-dessus consiste à appliquer le Laplacien à une fonction $h$ sur le nœud $i$, qui est la valeur de $h_i$ moins la valeur moyenne sur ses nœuds voisins $h_j$. Fondamentalement, si le signal est très lisse, la valeur de Laplacien est faible et vice versa.

Étape 2 : Fonctions de Fourier

Voici la décomposition en valeur propre du graphe Laplacien :

\[\underset{n \times n}{\Delta}=\Phi^{T} \Lambda \Phi\]

Le Laplacien est factorisé en trois matrices, $\Phi ^ T$, $\Lambda$, $\Phi$.

$\Phi$ est défini ci-dessous, il contient des vecteurs colonnes, ou vecteurs propres de Lap $\phi_1$ à $\phi_n$, chacun de taille $n \times 1$, et ceux-ci sont aussi appelés fonctions de Fourier. Et les fonctions de Fourier forment une base orthonormée.

\[\begin{array}{l}\text { où } \underset{n \times n}{\Delta}\Phi=\left[\phi_{1}, \ldots, \phi_{n}\right]=\text { et } \Phi^{T} \Phi=\mathrm{I},\left\langle\phi_{k}, \phi_{k^{\prime}}\right\rangle=\delta_{k k^{\prime}} \\\end{array}\]

$\Lambda$ est une matrice diagonale avec des valeurs propres Laplaciennes, et sur la diagonale se trouvent $\lambda_1$ à $\lambda_n$. Et d’après les applications normalisées, ces valeurs sont généralement comprises entre $0$ et $2$. Ces valeurs sont également connues sous le nom de « spectre du graphe ». Voir la formule ci-dessous.

\[\begin{array}{c}\text { où } \underset{n \times n}\Lambda=\operatorname{diag}\left(\lambda_{1}, \ldots, \lambda_{n}\right) \text { et } 0 \leq \lambda_{1} \leq \ldots \leq \lambda_{n}=\lambda_{\max } \leq 2\end{array}\]

Ci-dessous un exemple de vérification de la décomposition de la valeur propre. La matrice Laplacienne $\Lambda$ est multipliée par un vecteur propre $\phi_k$, la forme du résultat est $n \times 1$ et le résultat est $\lambda_k \phi_k$.

\[\begin{array}{ll}\text { et } \underset{n \times 1}{\Delta \phi_{k}}=\lambda_{k} \phi_{k}, & k=1, \ldots, n \\ & \end{array}\]

L’image ci-dessous est la visualisation des vecteurs propres du Laplacien euclidien 1D.

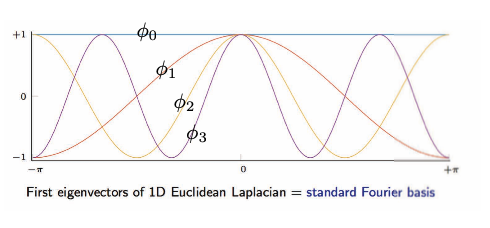
Figure 16 : Grille/domaine euclidien : vecteurs propres du Laplacien euclidien 1D.

Pour le domaine des graphes, de gauche à droite, se trouvent les première, deuxième, troisième, …, fonctions de Fourier d’un graphe. Par exemple, $\phi_1$ a des oscillations de valeurs positives (rouge) et négatives (bleu), de même pour $\phi2$, $\phi3$. Ces oscillations dépendent de la topologie d’un graphe, qui est liée à la géométrie des graphes tels que les communautés, les hubs, etc, et c’est utile pour le regroupement des graphes. Voir ci-dessous.

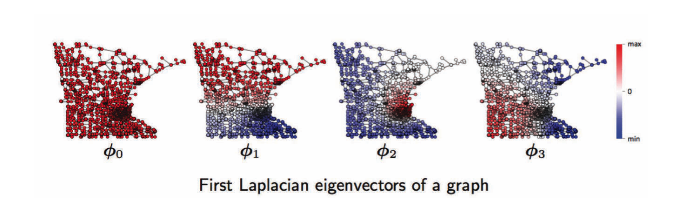
Figure 17 : Domaine du graphe : fonctions de Fourier d'un graphe

Étape 3 : Transformée de Fourier

\[\begin{aligned} \underset{n \times 1} h &=\sum_{k=1}^{n} \underbrace{\left\langle\phi_{k}, h\right\rangle}_{\mathcal{F}(h)_{k}=\hat{h}_{k}=\phi_{k}^{T} h}\underset{n \times 1}{\phi_{k}} \\\N - &=\sum_{k=1}^{n} \hat{h}_{k} \phi_{k} \\\N - &=\underbrace{\Phi \hat{h}}_{ \mathcal{F}^{-1}(\hat{h}) } \end{aligned}\]

Séries de Fourrier : décomposer la fonction $h$ avec les fonctions de Fourier.

Prendre la fonction $h$ et la projeter sur chaque fonction de Fourier $\phi_k$, ce qui donne le coefficient de la série de Fourier de $k$, une échelle, puis le multiplier par la fonction $\phi_k$.

La transformée de Fourier consiste essentiellement à projeter une fonction $h$ sur les fonctions de Fourier. Les résultats sont les coefficients des séries de Fourier.

Transformation de Fourier/ coefficients des séries de Fourier

\[\begin{aligned} \underset{n \times 1}{\mathcal{F}(h)} &=\Phi^{T} h \\ &=\hat{h} \end{aligned}\]

Transformée de Fourier inverse

\[\begin{aligned} \underset{n \times 1}{\mathcal{F}^{-1}(\hat{h})} &=\Phi \hat{h} \\\\Phi \Phi^{T} h=h \quad \text { car } \mathcal{F}^{-1} \circ \mathcal{F}=\Phi \Phi^{T}=\mathrm{I} \end{aligned}\]

Les transformées de Fourier sont des opérations linéaires, qui multiplient une matrice $\Phi^{T}$ par un vecteur $h$.

Étape 4 : Théorème des convolutions

La transformée de Fourier de la convolution de deux fonctions est le produit élément par élément de leurs transformées de Fourier.

\[\begin{aligned} \underset{n \times 1} {w * h} &=\underbrace{\mathcal{F}^{-1}}_{\Phi}(\underbrace{\mathcal{F}(w)}_{\Phi^{T} w=\hat{w}} \odot \underbrace{\mathcal{F}(h)}_{\Phi^{T} h}) \\ &=\underset{n \times n}{\Phi}\left( \underset{n \times 1}{\hat{w}}\odot \underset{n \times 1}{\Phi^{T} h}\right) \\ &=\Phi\left(\underset{n \times n}{\hat{w}(\Lambda)} \underset{n \times 1}{\Phi^{T} h}\right) \\ &=\Phi \hat{w}(\Lambda) \Phi^{T} h \\ &=\hat{w}(\underbrace{\Phi \Lambda \Phi^{T}}_{\Delta}) h \\ &=\underset{n \times n}{\hat{w}(\Delta)} \underset{n \times1}h \\ & \end{aligned}\]

L’exemple ci-dessus est la convolution de $w$ et $h$, tous deux de forme $n \times 1$, elle est égale à l’inverse de la transformée de Fourier du produit élément par élément entre la transformée de Fourier de $w$ et de $h$. La formule ci-dessus montre qu’elle est également égale à la multiplication matricielle de $\hat{w}(\Delta)$ et de $h$.

La convolution de deux fonctions sur les graphes $h$ et $w$ consiste à prendre la fonction de spectre de $w$, à l’appliquer au Laplacien et à la multiplier par $h$. C’est la définition de la convolution du spectre. Cependant, la complexité du calcul est de $\mathrm{O}\left(n^{2}\right)$, alors que $n$ est le nombre de nœuds du graphe.

Limitation

La convolution spectrale par rapport au domaine du graphe n’est pas une invariance au décalage, ce qui signifie que si elle est décalée, la forme de la fonction peut également être modifiée. Alors que dans le domaine de la grille/euclidienne, elle ne l’est pas.

Livre recommandé

Spectral graph theory de Fan Chung, (analyse harmonique, théorie des graphes, problèmes combinatoires, optimisation)

---

📝 Bilal Munawar, Alexander Bienstock, Can Cui, Shaoling Chen
Loïck Bourdois
27 Apr 2020