Introduction à la descente de gradient et à l’algorithme de rétropropagation

Algorithme de l’optimisation de la descente de gradient

Modèles paramétrés

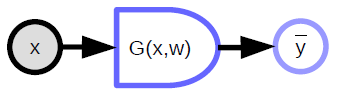
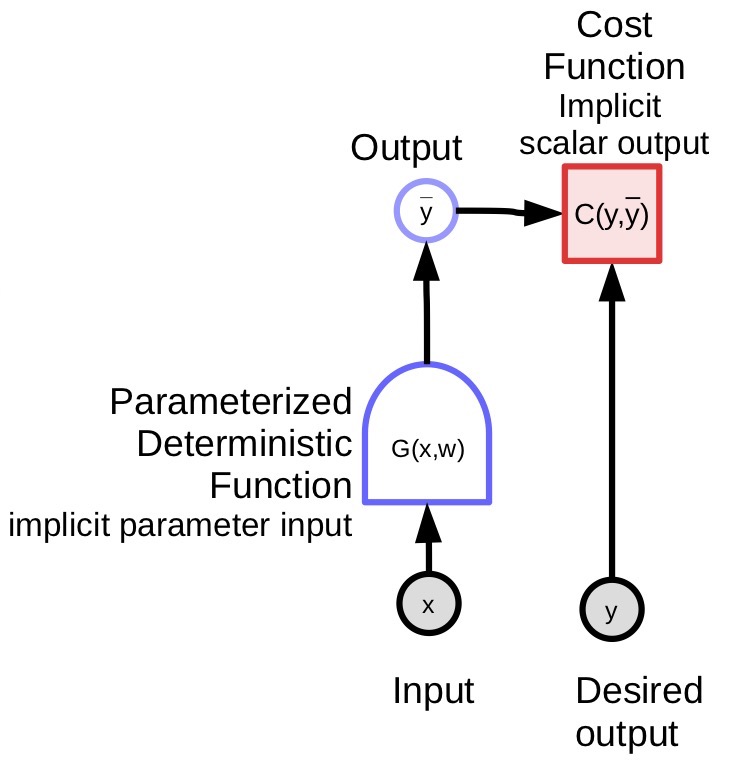
Les modèles paramétrés sont simplement des fonctions qui dépendent d’entrées et de paramètres pouvant être entrainés. Il n’y a pas de différence fondamentale entre les deux, si ce n’est que les paramètres pouvant être entrainés sont partagés entre les échantillons d’entraînement alors que l’entrée varie d’un échantillon à l’autre. Dans la plupart des cadres d’apprentissage profond, les paramètres sont implicites, c’est-à-dire qu’ils ne sont pas transmis lorsque la fonction est appelée. Ils sont « enregistrés dans la fonction », pour ainsi dire, du moins dans les versions orientées objet des modèles.

Le modèle paramétré prend une entrée, possède un vecteur de paramètres et produit une sortie. Dans l’apprentissage supervisé, cette sortie va dans la fonction de coût $C(y,\bar{y}$), qui compare la sortie réelle ${y}$ avec la sortie du modèle $\bar{y}$. Le graphe de calcul pour ce modèle est présenté à la figure 1.

Figure 1 : Représentation sous forme de graphe d'un modèle paramétré

Exemples de fonctions paramétrées :

• Modèle linéaire : la somme pondérée des composantes du vecteur d’entrée :

  \[\bar{y} = \sum_i w_i x_i, C(y,\bar{y}) = \Vert y - \bar{y}\Vert^2\]

• Voisin le plus proche : il y a une entrée $\vect{x}$ et une matrice de poids $\matr{W}$ avec chaque ligne de la matrice indexée par $k$. La sortie est la valeur de $k$ qui correspond à la ligne de $\matr{W}$ la plus proche de $\vect{x}$ :

Les modèles paramétrés peuvent également comporter des fonctions compliquées.

Notations des schémas de calcul

• Variables (tenseur, scalaire, continues, discrètes) :
• • est une entrée observée dans le système
  • est une variable calculée qui est produite par une fonction déterministe

• Fonctions déterministes :

  

  • Prend en compte de multiples entrées et peut produire de multiples sorties
  • Possède une variable paramètre implicite (${w}$)
  • Le côté arrondi indique la direction dans laquelle c’est plus facile à calculer. Dans le diagramme ci-dessus, il est plus facile de calculer ${\bar{y}}$ à partir de ${x}$ que l’inverse

• Fonction à valeur scalaire

  

  • Utilisée pour représenter les fonctions de coût
  • A une sortie scalaire implicite
  • Prend plusieurs entrées et produit une seule valeur (généralement la distance entre les entrées)

Fonctions de perte

Une fonction de perte est une fonction qui est minimisée pendant l’entraînement. Il existe deux types de pertes :

1) Perte par échantillon :

2) Perte moyenne :

Pour toute série d’échantillons $S = \lbrace(x[p],y[p]) \mid p \in \lbrace 0, \cdots, P-1 \rbrace \rbrace$, la perte moyenne sur l’ensemble des $S$ est donnée par :

Figure 2 : Graphe pour le modèle avec perte moyenne

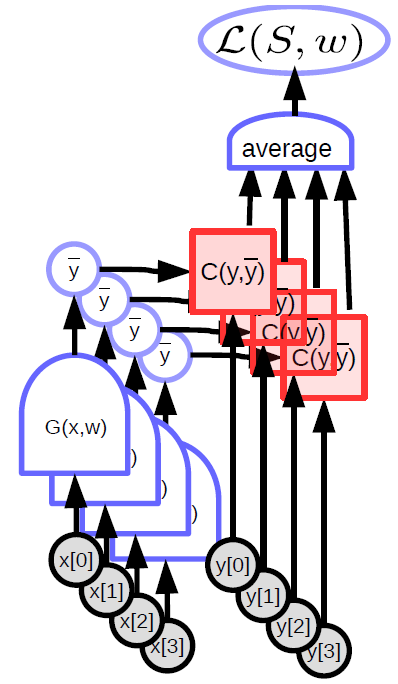Dans le paradigme standard de l’apprentissage supervisé, la perte (par échantillon) est simplement le résultat de la fonction de coût. L’apprentissage machine consiste principalement à optimiser les fonctions (généralement en les minimisant). Il peut également s’agir de trouver des équilibres de Nash entre deux fonctions, comme dans le cas des GANs (Generative adversarial networks). Cela se fait en utilisant des méthodes basées sur le gradient, mais pas nécessairement sur la descente du gradient.

Descente de gradient

Une méthode basée sur le gradient est une méthode/algorithme qui trouve les minima d’une fonction, en supposant que l’on peut facilement calculer le gradient de cette fonction. Elle suppose que la fonction est continue et différentiable presque partout (il n’est pas nécessaire qu’elle soit différentiable partout).

Intuition de la descente du gradient :

Imaginez que vous êtes dans une montagne au milieu d’une nuit brumeuse. Comme vous voulez descendre jusqu’au village et que vous n’avez qu’une vision limitée, vous regardez autour de vous pour trouver la direction de la descente la plus raide et faites un pas dans cette direction.

Différentes méthodes de descente de gradient :

• Mise à jour de la descente de gradient complète (par batch) :

  \[w \leftarrow w - \eta \frac{\partial L(S,w)}{\partial w}\]

• Pour la SGD (la Descente de Gradient Stochastique de l’anglais Stochastic Gradient Descent), la règle de mise à jour devient :

  • Choisissez un $p \in \lbrace 0, \cdots, P-1 \rbrace$, puis mettez à jour

    \[w \leftarrow w - \eta \frac{\partial L(x[p], y[p],w)}{\partial w}\]

    où ${w}$ représente le paramètre à optimiser.

    $\eta$ est une constante ici mais dans des algorithmes plus sophistiqués, il pourrait s’agir d’une matrice.

Si c’est une matrice semi-définie positive, nous continuerons à descendre, mais pas nécessairement dans le sens de la descente la plus raide. En fait, la direction de la descente la plus raide n’est pas toujours celle dans laquelle nous voulons aller.

Si la fonction n’est pas différentiable, c’est-à-dire si elle a un trou, si elle est en forme d’escalier ou si elle est plate (la pente ne donne alors aucune information), il faut recourir à d’autres méthodes appelées méthodes d’ordre 0 ou méthodes sans gradient. L’apprentissage profond est une méthode basée sur le gradient.

Cependant, le RL (Apprentissage par renforcement de l’anglais Reinforcement Learning) implique une estimation du gradient sans la forme explicite du gradient. Un exemple est un robot apprenant à faire du vélo où le robot tombe de temps en temps. La fonction objectif mesure la durée pendant laquelle le vélo reste debout sans tomber. Malheureusement, il n’y a pas de gradient pour la fonction objectif. Le robot doit essayer différentes choses.

La fonction de coût en RL n’est pas différenciable la plupart du temps, mais le réseau qui calcule la sortie est basé sur un gradient. C’est la principale différence entre l’apprentissage supervisé et l’apprentissage par renforcement. Dans ce dernier cas, la fonction de coût $C$ n’est pas différenciable. En fait, elle est totalement inconnue. Elle renvoie simplement une sortie lorsque des entrées lui sont fournies, comme une boîte noire. Cela la rend très inefficace et constitue l’un des principaux inconvénients du RL. En particulier lorsque le vecteur de paramètres est à haute dimension (ce qui implique un énorme espace de solution à rechercher, rendant difficile de trouver où se déplacer).

Une technique très populaire en RL est la méthode Acteur-Critique (AC). Une méthode critique consiste essentiellement en un second module C qui est un module connu et pouvant être entraîné. On peut entraîner le module C, qui est différenciable, à se rapprocher de la fonction de coût / fonction de récompense. La récompense est un coût négatif, pouvant être vue comme une punition. C’est une façon de rendre la fonction de coût différentiable, ou du moins de l’approcher par une fonction différentiable afin de pouvoir faire de la rétropropagation.

Avantages de la SGD et de la rétropropagation pour les réseaux de neurones traditionnels

Avantages de la descente de gradient stochastique (SGD)

En pratique, nous utilisons un gradient stochastique pour calculer le gradient de la fonction objectif sans les paramètres. Au lieu de calculer le gradient complet de la fonction objectif, qui est la moyenne de tous les échantillons, le gradient stochastique ne prend qu’un échantillon, calcule la perte $L$, et le gradient de la perte avec les paramètres. Puis on fait un pas dans la direction du gradient négatif.

Dans la formule, $w$ est approché par $w$ moins la taille du pas, multiplié par le gradient de la fonction de perte par échantillon avec les paramètres pour un échantillon donné, ($x[p]$,$y[p]$).

Si nous faisons cela sur un seul échantillon, nous obtenons une trajectoire très bruyante comme le montre la figure 3. Au lieu que la perte soit directement descendante, elle est stochastique. Chaque échantillon tire la perte vers une direction différente. En prendre la moyenne nous tire au minimum de la moyenne. Bien que cela semble inefficace, c’est beaucoup plus rapide que la descente par batch, au moins dans le contexte de l’apprentissage machine, lorsque les échantillons ont une certaine redondance.

Figure 3 : Trajectoire d'une descente de gradient stochastique pour une mise à jour par échantillon

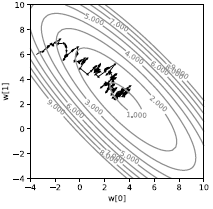En pratique, nous utilisons des batchs (des lots) au lieu de faire une descente de gradient stochastique sur un seul échantillon. Nous calculons la moyenne du gradient sur un lot d’échantillons, et non sur un seul échantillon, puis nous effectuons une étape. La seule raison pour laquelle nous faisons cela est que nous pouvons utiliser plus efficacement le matériel existant (c’est-à-dire les GPUs, les CPUs multi-cœurs) car il est plus facile de les paralléliser. La mise en lots est la façon la plus simple de paralléliser.

Réseau neuronal traditionnel

Les réseaux neuronaux traditionnels sont essentiellement des couches intercalées d’opérations linéaires et d’opérations non linéaires ponctuelles. Pour les opérations linéaires, il s’agit conceptuellement d’une simple multiplication matrice-vecteur. Nous prenons le vecteur (d’entrée) multiplié par une matrice formée par les poids. Le deuxième type d’opération consiste à prendre toutes les composantes du vecteur des sommes pondérées et à les faire passer par une simple non-linéarité (c’est-à-dire $\texttt{ReLU}(\cdot)$, $\tanh(\cdot)$, …).

Figure 4 : Réseau neuronal traditionnel

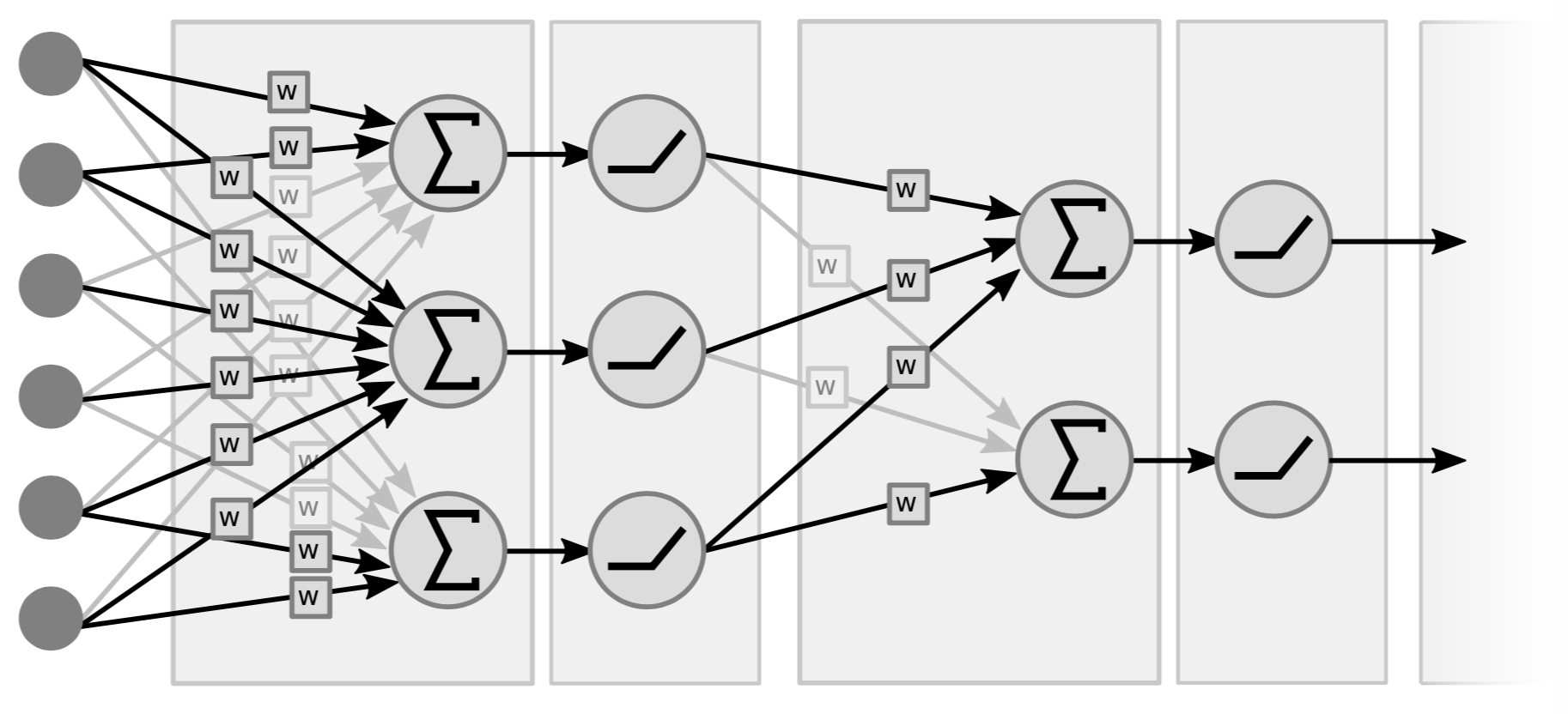La figure 4 est un exemple de réseau à deux couches, car ce sont les paires (c’est-à-dire linéaire+non linéaire) qui comptent. Certaines personnes l’appellent un réseau à 3 couches parce qu’elles comptent les variables. Notez que s’il n’y a pas de non-linéarités au milieu, nous pouvons tout aussi bien avoir une seule couche car le produit de deux fonctions linéaires est une fonction linéaire.

La figure 5 montre comment les blocs fonctionnels linéaires et non linéaires du réseau s’empilent :

Figure 5 : L'intérieur des blocs linéaires et non linéaires

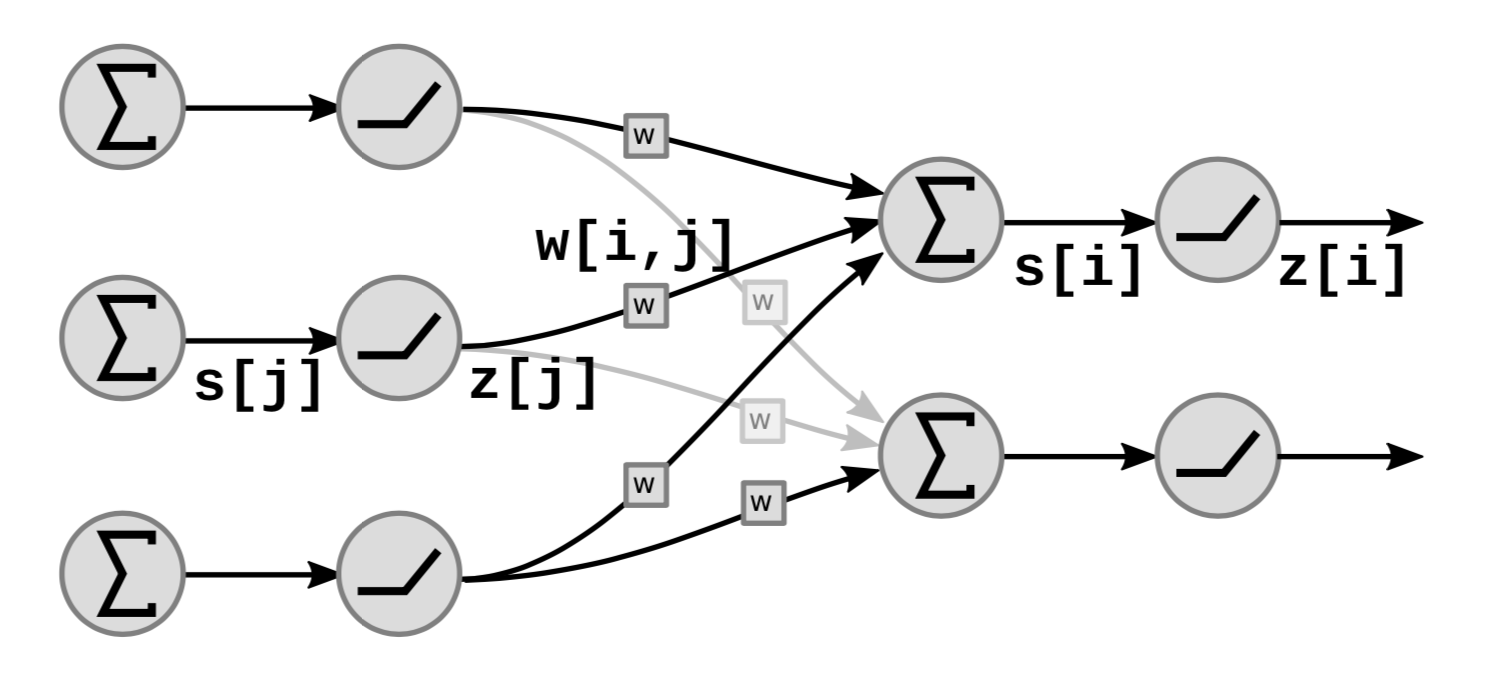Dans la figure, $s[i]$ est la somme pondérée de l’unité ${i}$ qui est calculée comme suit

où $UP(i)$ désigne les prédécesseurs de $i$ et $z[j]$ est la $j$ième sortie de la couche précédente.

La sortie $z[i]$ est calculée comme suit

où $f$ est une fonction non linéaire.

Rétropropagation par une fonction non linéaire

La première façon de faire de la rétropropagation est de rétropropager par une fonction non linéaire. Nous prenons une fonction non linéaire particulière $h$ du réseau et nous laissons tout le reste dans la boîte noire.

Figure 6 : Rétropropagation par une fonction non linéaire

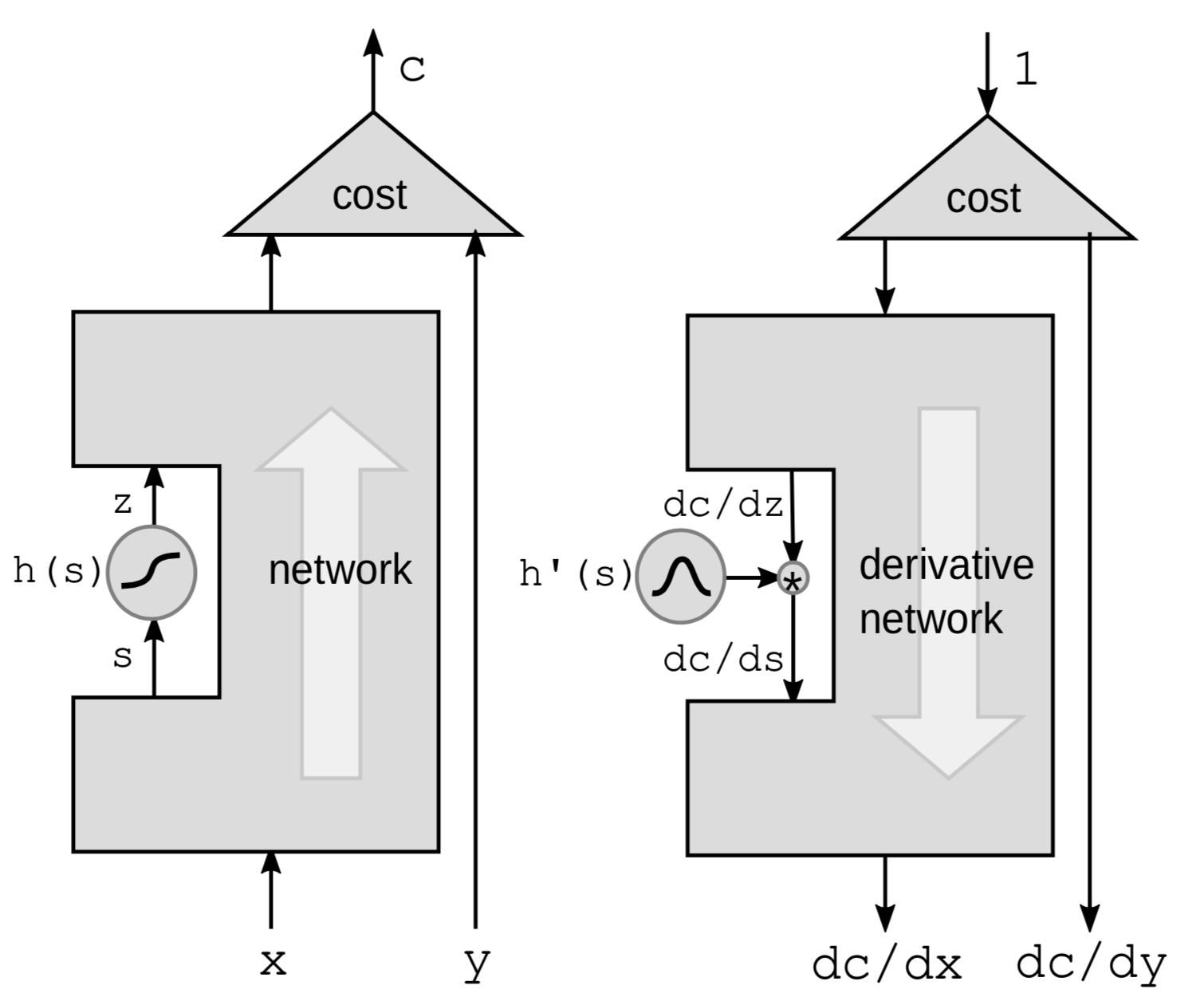Nous allons utiliser la règle de la chaîne pour calculer les gradients :

où $h’(s)$ est le dérivé de $z$ par rapport à $s$ représenté par $\frac{\mathrm{d}z}{\mathrm{d}s}$.

Pour que le lien entre les dérivés soit clair, nous réécrivons la formule ci-dessus comme suit

Par conséquent, si nous avons une chaîne de ces fonctions dans le réseau, nous pouvons faire une rétropropagation en multipliant par les dérivées de toutes les fonctions ${h}$ l’une après l’autre jusqu’au fond.

Il est plus intuitif de penser en termes de perturbations. Perturber $s$ par $\mathrm{d}s$ perturbera $z$ par :

Cela perturbera à son tour $C$ par :

Une fois de plus, nous nous retrouvons avec la même formule que celle présentée ci-dessus.

Rétropropagation par une somme pondérée

Pour un module linéaire, nous faisons la rétropropagation par une somme pondérée. Ici, nous considérons l’ensemble du réseau comme une boîte noire, à l’exception de 3 connexions allant d’une variable ${z}$ à un tas de variables $s$.

Figure 7 : Rétropropagation par la somme pondérée

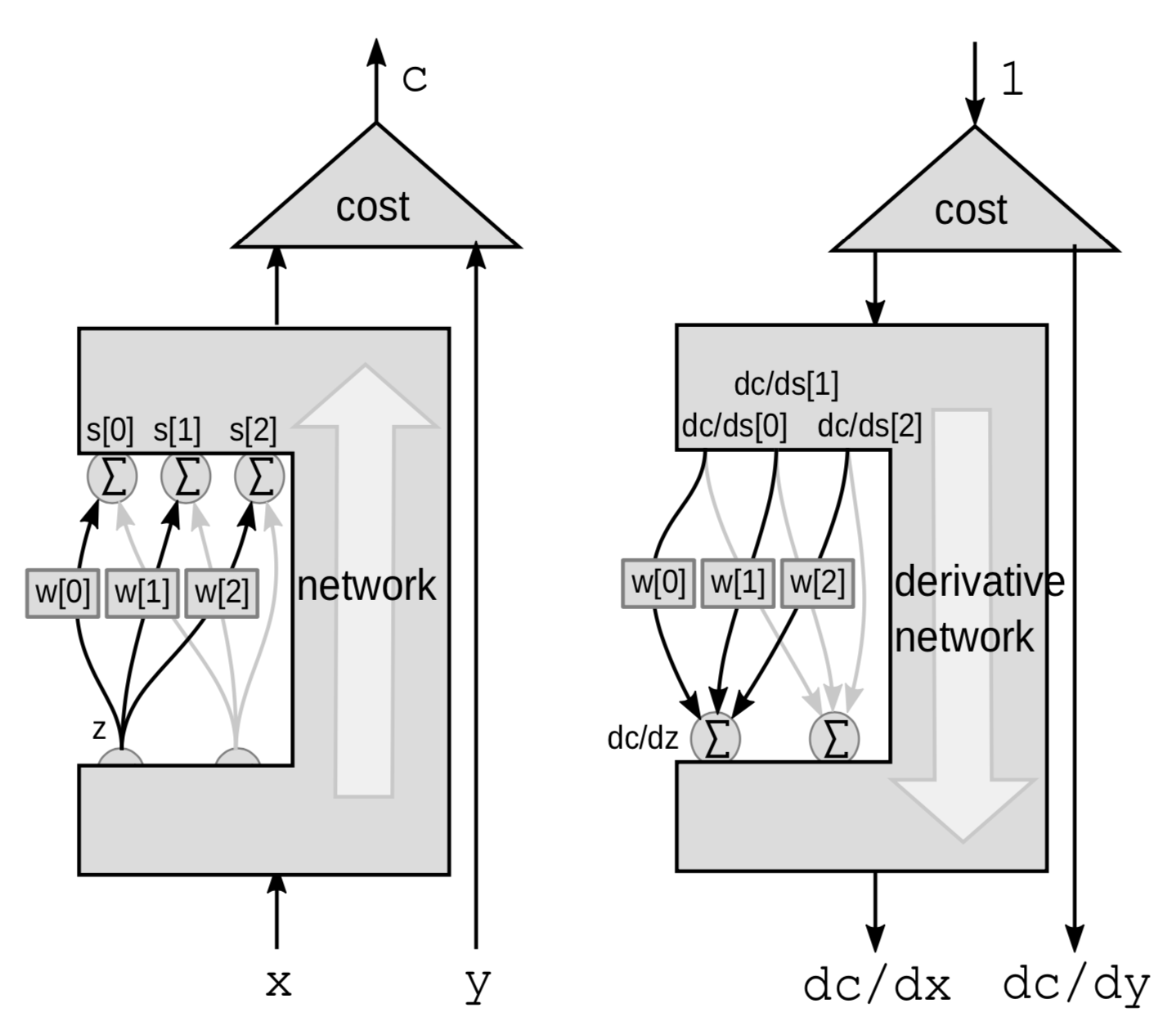Cette fois, la perturbation est une somme pondérée. $Z$ influence plusieurs variables. Perturber $z$ de $\mathrm{d}z$ perturbera $s[0]$, $s[1]$ et $s[2]$ de :

Cela perturbera $C$ de

Ainsi, $C$ va varier en fonction de la somme des 3 variations :

Implémentation PyTorch d’un reseau neuronal et de l’algorithme de rétropropagation

Schéma fonctionnel d’un réseau neuronal traditionnel

• Blocs linéaires $s_{k+1}=w_kz_k$

• Blocs non-linéaires $z_k=h(s_k)$

  

$w_k$ est une matrice, $z_k$ un vecteur et $h$ l’application de la fonction scalaire ${h}$ à chaque composant. Il s’agit d’un réseau neuronal à trois couches avec des paires de fonctions linéaires et non linéaires, bien que la plupart des réseaux neuronaux modernes n’aient pas de séparations linéaires et non linéaires aussi nettes et sont plus complexes.

Implementation en PyTorch

import torch
from torch import nn
image = torch.randn(3, 10, 20)
d0 = image.nelement()

class mynet(nn.Module):
    def __init__(self, d0, d1, d2, d3):
        super().__init__()
        self.m0 = nn.Linear(d0, d1)
        self.m1 = nn.Linear(d1, d2)
        self.m2 = nn.Linear(d2, d3)

    def forward(self,x):
        z0 = x.view(-1)  # aplatit le tenseur d'entrée
        s1 = self.m0(z0)
        z1 = torch.relu(s1)
        s2 = self.m1(z1)
        z2 = torch.relu(s2)
        s3 = self.m2(z2)
        return s3
model = mynet(d0, 60, 40, 10)
out = model(image)

Nous pouvons implémenter des réseaux neuronaux avec des classes orientées objet dans PyTorch. Tout d’abord, nous définissons une classe pour le réseau neuronal et nous initialisons les couches linéaires dans le constructeur en utilisant la classe prédéfinie nn.Linear. Les couches linéaires doivent être des objets séparés car chacune d’entre elles contient un vecteur de paramètres. La classe nn.Linear ajoute aussi implicitement le vecteur de biais. Ensuite, nous définissons une fonction directe sur la façon de calculer les sorties avec la fonction torch.relu comme activation non linéaire. Nous n’avons pas besoin d’initialiser des fonctions ReLU séparées car elles n’ont pas de paramètres.

Nous n’avons pas besoin de calculer le gradient nous-mêmes puisque PyTorch sait comment propager en arrière et calculer les gradients avec la fonction forward.

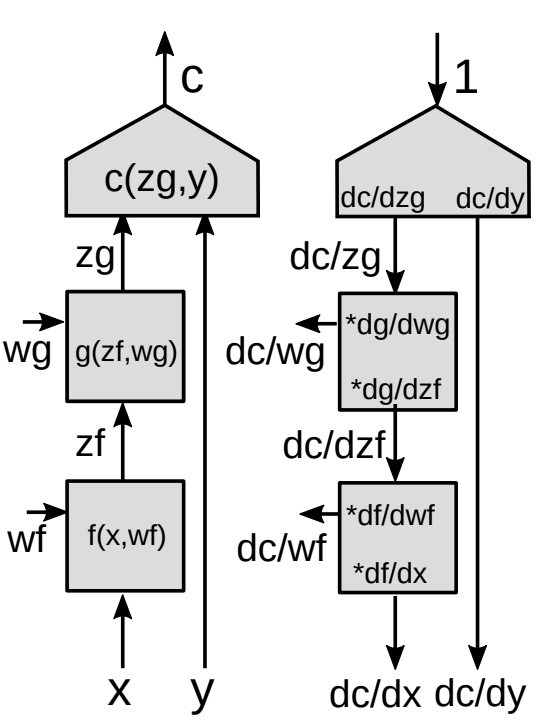
Rétropropagation par le biais d’un module fonctionnel

Nous présentons maintenant une forme plus généralisée de rétropropagation.

Figure 8 : Rétropropagation par le biais d’un module fonctionnel

• Utilisation du théorème de dérivation des fonctions composées (appelé aussi règle de la chaîne) pour les fonctions vectorielles :

  \[z_g : [d_g\times 1]\] \[z_f :[d_f\times 1]\] \[\frac{\partial c}{\partial{z_f}}=\frac{\partial c}{\partial{z_g}}\frac{\partial {z_g}}{\partial{z_f}}\] \[[1\times d_f]= [1\times d_g]\times[d_g\times d_f]\]

C’est la formule de base pour $\frac{\partial c}{\partial{z_f}}$ en utilisant la règle de la chaîne. Notez que le gradient d’une fonction scalaire par rapport à un vecteur est un vecteur de même taille que le vecteur par rapport auquel vous faites la différence. Afin de rendre les notations cohérentes, il s’agit d’un vecteur ligne au lieu d’un vecteur colonne.

• Matrice jacobienne :

  \[\left(\frac{\partial{z_g}}{\partial {z_f}}\right)_{ij}=\frac{(\partial {z_g})_i}{(\partial {z_f})_j}\]

Nous avons besoin de $\frac{\partial {z_g}}{\partial {z_f}}$ (entrées de la matrice jacobienne) pour calculer le gradient de la fonction de coût par rapport à $z_f$, étant donné le gradient de la fonction de coût par rapport à $z_g$. Chaque entrée $ij$ est égale à la dérivée partielle de la composante $i$ème du vecteur de sortie par rapport à la composante $j$ème du vecteur d’entrée.

Si nous avons une cascade de modules, nous continuons à multiplier les matrices jacobiennes de tous les modules qui descendent et nous obtenons les gradients par rapport à de toutes les variables internes.

Rétropropagation par le biais d’un graphe à plusieurs niveaux

Considérons une pile de plusieurs modules dans un réseau de neurones, comme le montre la figure 9.

Figure 9 : Rétropropagation par le biais d’un graphe à plusieurs niveaux

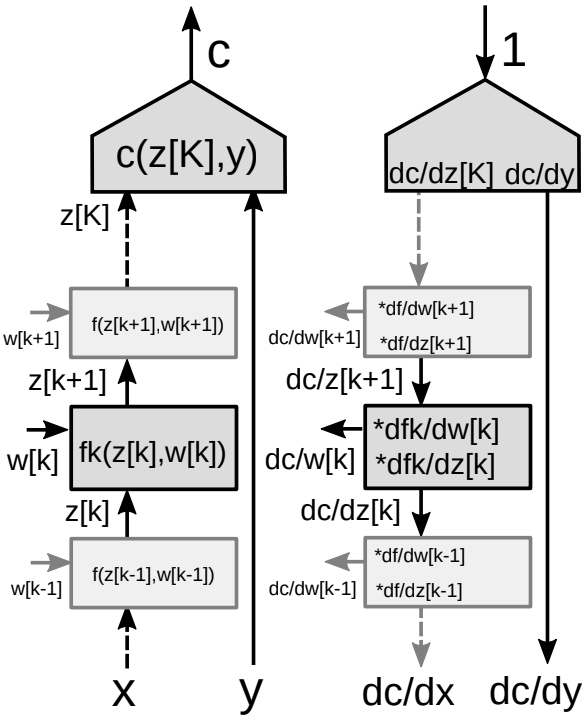Pour l’algorithme de rétropropagation, nous avons besoin de deux ensembles de gradients : un par rapport aux états (chaque module du réseau) et un par rapport aux poids (tous les paramètres d’un module particulier). Nous avons donc deux matrices jacobiennes associées à chaque module. Nous pouvons à nouveau utiliser la règle de la chaîne pour la rétropropagation.

• Utilisation de la règle en chaîne pour les fonctions vectorielles :

  \[\frac{\partial c}{\partial {z_k}}=\frac{\partial c}{\partial {z_{k+1}}}\frac{\partial {z_{k+1}}}{\partial {z_k}}=\frac{\partial c}{\partial {z_{k+1}}}\frac{\partial f_k(z_k,w_k)}{\partial {z_k}}\] \[\frac{\partial c}{\partial {w_k}}=\frac{\partial c}{\partial {z_{k+1}}}\frac{\partial {z_{k+1}}}{\partial {w_k}}=\frac{\partial c}{\partial {z_{k+1}}}\frac{\partial f_k(z_k,w_k)}{\partial {w_k}}\]

• Deux matrices jacobiennes pour le module :

  • Une en ce qui concerne $z[k]$.
  • Une en ce qui concerne $w[k]$.