Techniques d’optimisation II

Méthodes adaptatives

La SGD avec momentum est actuellement la méthode d’optimisation de pointe pour de nombreux problèmes d’apprentissage machine. Mais il existe d’autres méthodes, généralement appelées méthodes adaptatives qui sont particulièrement utiles pour les problèmes mal conditionnés (si la SGD ne fonctionne pas).

Dans la formule de la SGD, chaque poids dans le réseau est mis à jour en utilisant une équation avec le même taux d’apprentissage global ($\gamma$). Ici, pour les méthodes adaptatives, nous adaptons un taux d’apprentissage pour chaque poids individuellement. À cette fin, nous utilisons les informations que nous obtenons des gradients pour chaque poids.

Les réseaux souvent utilisés en pratique ont une structure différente dans plusieurs parties d’eux. Par exemple, les premières parties d’un ConvNet peuvent être des couches de convolution très peu profondes sur de grandes images et plus loin dans le réseau, nous pouvons avoir des convolutions d’un grand nombre de canaux sur de petites images. Ces deux opérations sont très différentes, de sorte qu’un taux d’apprentissage qui fonctionne bien pour le début du réseau peut ne pas fonctionner correctement pour les dernières parties du réseau. Cela signifie qu’un taux d’apprentissage adaptatif par couche pourrait être utile.

Les poids dans la dernière partie du réseau (4096 dans la figure 1 ci-dessous) dictent directement la sortie et ont un effet très fort sur celle-ci. C’est pourquoi nous avons besoin de taux d’apprentissage plus faibles pour ces derniers. En revanche, les pondérations antérieures auront des effets individuels plus faibles sur la sortie, en particulier lorsqu’elles sont initialisées de manière aléatoire.

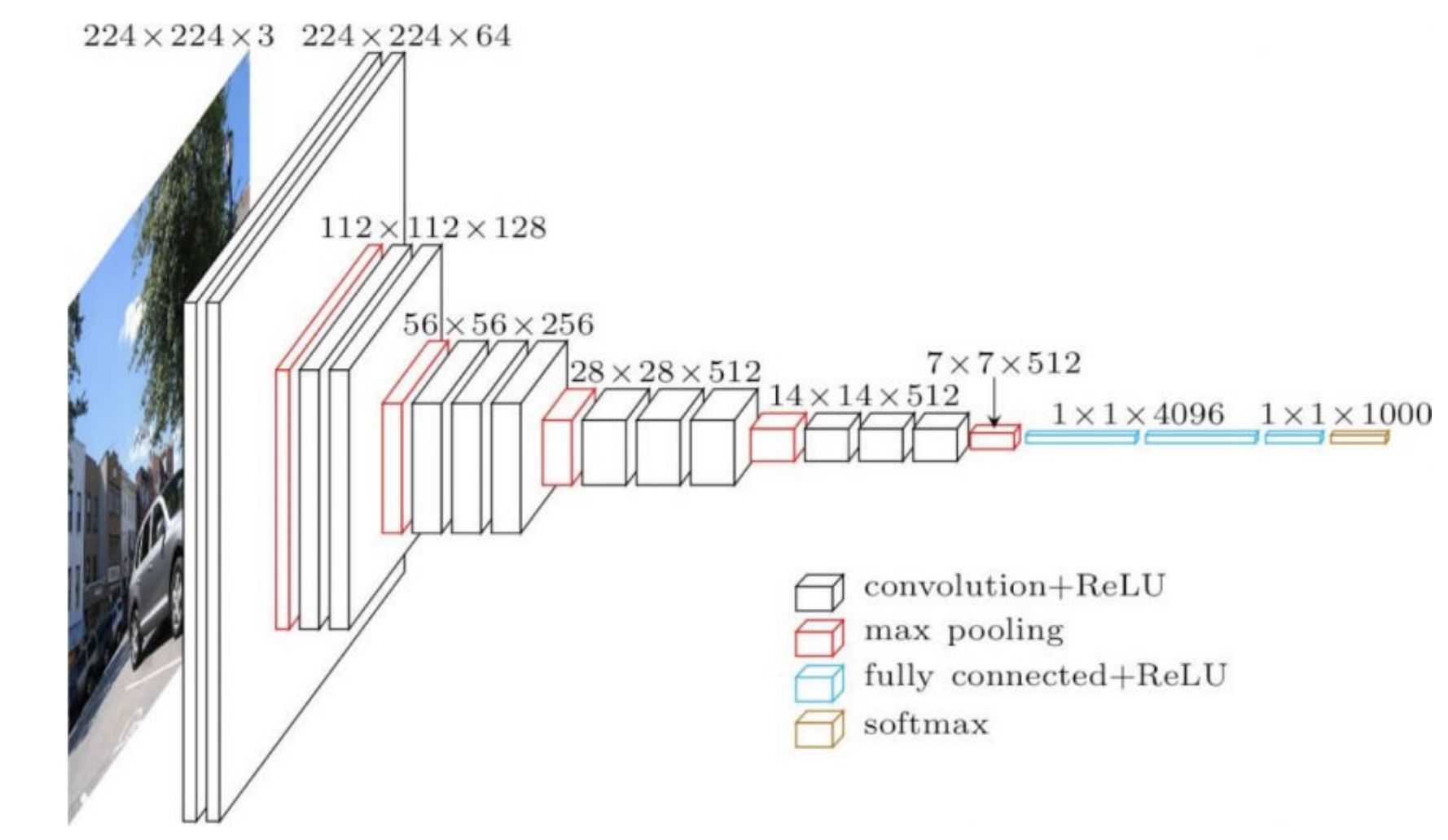
Figure 1 : VGG16

RMSprop

L’idée clé de la Root Mean Square Propagation (propagation quadratique moyenne) est que le gradient est normalisé par sa racine carrée moyenne.

Dans l’équation ci-dessous, l’élévation au carré du gradient indique que chaque élément du vecteur est élevé au carré individuellement.

où $\gamma$ est le taux d’apprentissage global, $\epsilon$ est une valeur de l’ordre de $10^{-7}$ ou $10^{-8}$) afin d’éviter les erreurs dû à la division par zéro, et $v_{t+1}$ est l’estimation du 2ème moment.

Nous mettons à jour $v$ pour estimer cette quantité bruyante via une moyenne mobile exponentielle qui est une façon standard de maintenir une moyenne d’une quantité pouvant changer dans le temps. Nous devons accorder un poids plus important aux nouvelles valeurs car elles fournissent davantage d’informations. Une façon d’y parvenir est de pondérer les anciennes valeurs de manière exponentielle. Les valeurs très anciennes dans le calcul de $v$ sont pondérées à chaque étape par une constante $\alpha$, qui varie entre 0 et 1. Cela atténue les anciennes valeurs jusqu’à ce qu’elles ne soient plus une partie importante de la moyenne mobile exponentielle.

La méthode originale conserve une moyenne mobile exponentielle d’un second moment non central, donc nous ne soustrayons pas la moyenne ici. Le deuxième moment est utilisé pour normaliser par élément le gradient, ce qui signifie que chaque élément du gradient est divisé par la racine carrée de l’estimation du deuxième moment. Si la valeur attendue du gradient est faible, ce processus est similaire à la division du gradient par l’écart-type.

L’utilisation d’un petit $\epsilon$ au dénominateur ne diverge pas car lorsque $v$ est très petit, le momentum est également très petit.

ADAM

ADAM ou Adaptive Moment Estimation est une méthode couramment utilisée consistant en un RMSprop avec momentum. La mise à jour du momentum est convertie en une moyenne mobile exponentielle et nous n’avons pas besoin de changer le taux d’apprentissage lorsque nous traitons avec $\beta$. Tout comme pour RMSprop, nous prenons ici une moyenne mobile exponentielle du gradient au carré.

où $m_{t+1}$ est la moyenne mobile exponentielle du momentum.

La correction de biais qui est utilisée pour maintenir la moyenne mobile non biaisée pendant les premières itérations n’est pas présentée ici.

Côté pratique

Lors de l’entraînement des réseaux neuronaux, la SGD va souvent dans la mauvaise direction au début du processus, alors que RMSprop va dans la bonne direction. Cependant, RMSprop souffre du même bruit que la SGD normale, donc il rebondit autour de l’optimum de manière significative. Tout comme lorsque nous ajoutons un momentum à la SGD, nous obtenons le même type d’amélioration avec ADAM. C’est une bonne estimation, non bruyante, de la solution. Ainsi ADAM est généralement recommandé par rapport à RMSprop.

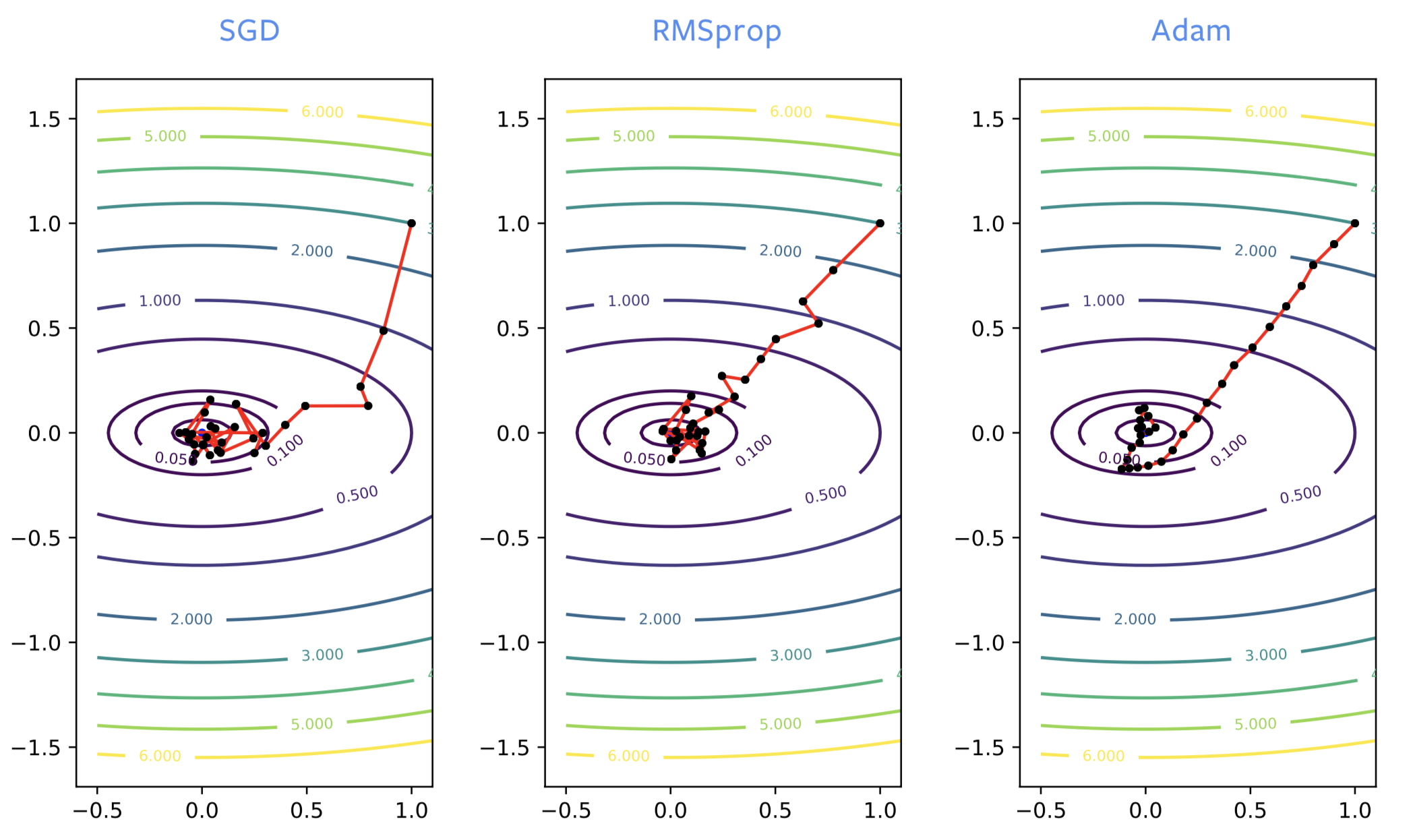
Figure 2 : SGD vs RMSprop vs ADAM

ADAM est nécessaire pour entraîner certains des modèles linguistiques. Pour optimiser les réseaux de neurones, il est généralement préférable d’utiliser la SGD avec momentum ou ADAM. Cependant, la théorie derrière ADAM est mal comprise et elle présente également plusieurs inconvénients :

• On peut montrer sur des problèmes de test très simples que la méthode ne converge pas.
• Elle est connue pour donner des erreurs de généralisation. Si le réseau est entraîné à donner une perte nulle sur les données sur lesquelles on l’a entraîné, il ne donnera pas une perte nulle sur d’autres données que le réseau n’aura jamais vus auparavant. Il est assez courant, en particulier pour les problèmes d’image, que nous obtenions des erreurs de généralisation pires que lorsque la SGD est utilisée. Cela peut venir du fait qu’il trouve le minimum local le plus proche, qu’il y ait moins de bruit dans ADAM, ou encore sa structure.
• Avec ADAM, nous devons garder en mémoire 3 paramètres, alors que la SGD en a besoin que de 2. Cela n’a pas vraiment d’importance, à moins que nous n’entrainions un modèle de l’ordre de plusieurs giga-octets, auquel cas il pourrait ne pas tenir en mémoire.
• 2 paramètres de momentum doivent être réglés au lieu d’un seul.

Couches de normalisation

Plutôt que d’améliorer les algorithmes d’optimisation, les couches de normalisation améliorent la structure même du réseau. Il s’agit de couches supplémentaires entre les couches existantes. L’objectif est d’améliorer les performances d’optimisation et de généralisation.

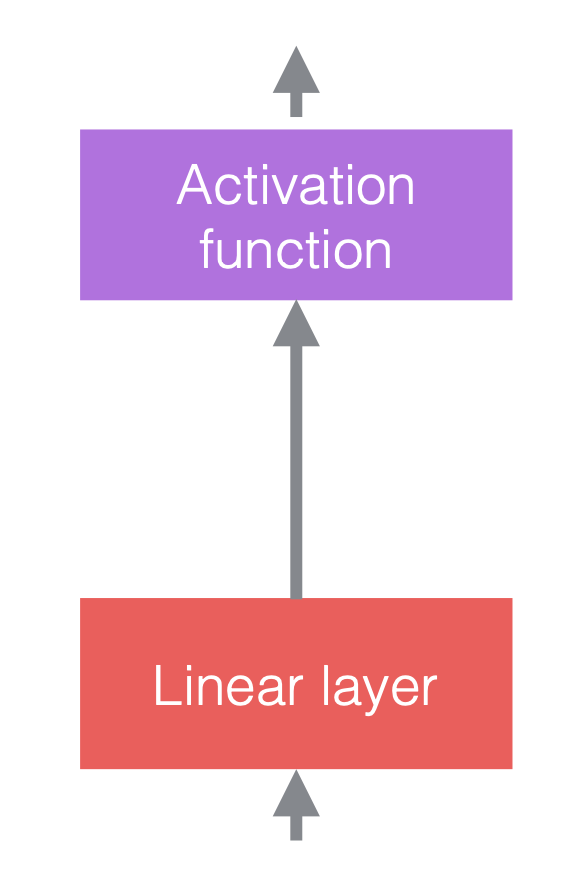
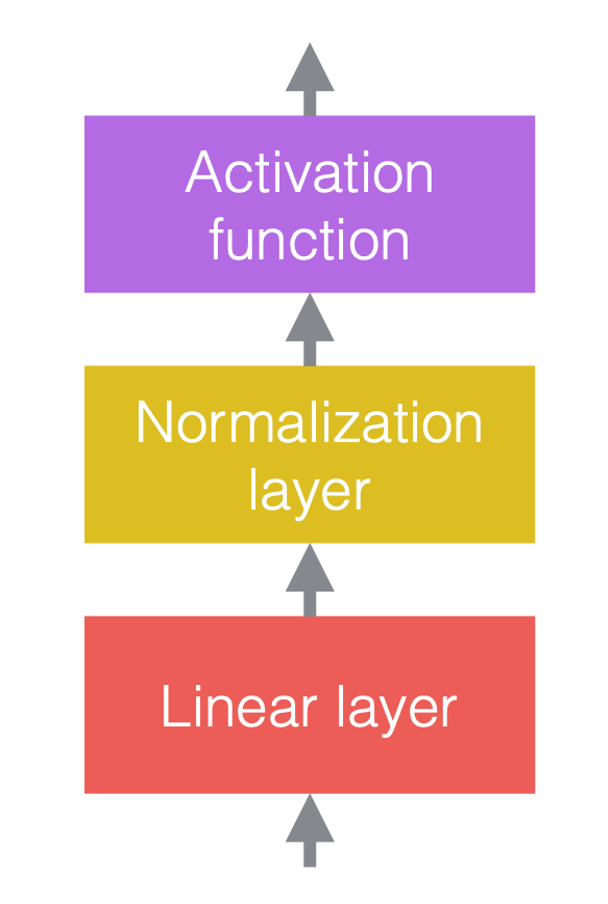
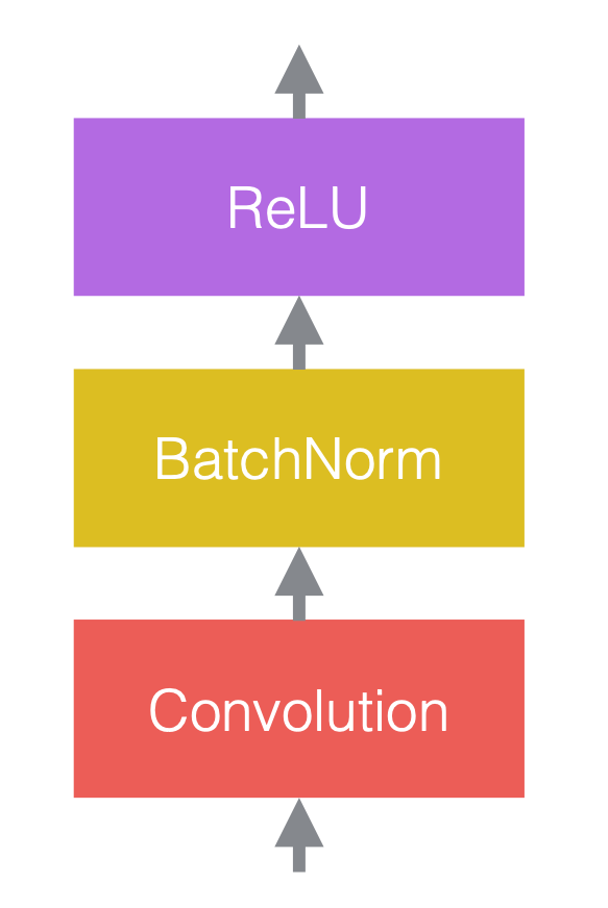
Dans les réseaux de neurones, nous alternons généralement des opérations linéaires et des opérations non linéaires. Les opérations non linéaires sont également connues sous le nom de fonctions d’activation, telles que la ReLU. Nous pouvons placer des couches de normalisation avant les couches linéaires ou après les fonctions d’activation. La pratique la plus courante consiste à les placer entre les couches linéaires et les fonctions d’activation comme dans la figure ci-dessous.

(a) Avant d’ajouter la normalisation	(b) Après avoir ajouté la normalisation	(c) Un exemple dans les ConvNets

Dans la figure 3(c), la convolution est la couche linéaire, suivie de la normalisation par batchs, puis d’une ReLU.

Notons que les couches de normalisation affectent les données qui passent, mais elles ne modifient pas la puissance du réseau dans le sens où, avec une configuration appropriée des poids, le réseau non normalisé peut toujours donner le même résultat qu’un réseau normalisé.

Opérations de normalisation

Il s’agit de la notation générique pour la normalisation :

où $x$ est le vecteur d’entrée, $y$ est le vecteur de sortie, $\mu$ est l’estimation de la moyenne de $x$, $\sigma$ est l’estimation de l’écart-type de $x$, $a$ est le coefficient d’apprentissage et $b$ est le terme de biais apprenant.

Sans les paramètres d’apprentissage $a$ et $b$, la distribution du vecteur de sortie $y$ a une moyenne fixe de 0 et un écart-type de 1. Le coefficient $a$ et le terme de biais $b$ maintiennent le pouvoir de représentation du réseau, c’est-à-dire que les valeurs de sortie peuvent toujours être sur une plage particulière. A noter que $a$ et $b$ n’inversent pas la normalisation car ce sont des paramètres qui peuvent être appris et qui sont beaucoup plus stables que $\mu$ et $\sigma$.

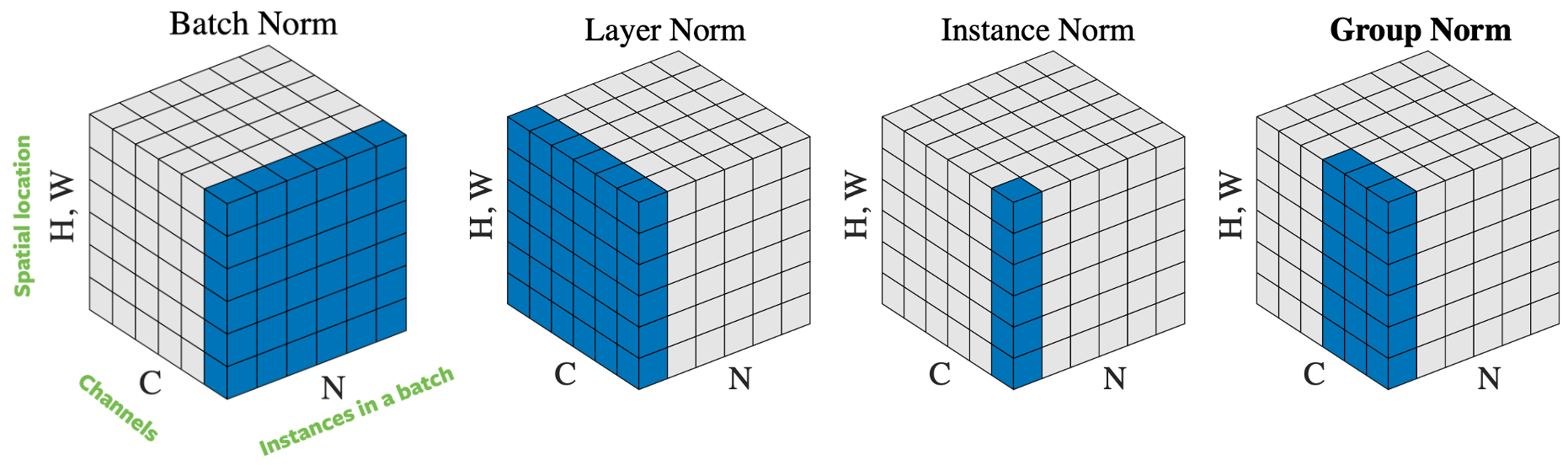
Figure 4 : Opérations de normalisation

Il existe plusieurs façons de normaliser le vecteur d’entrée, en fonction de la façon de sélectionner les échantillons à normaliser. La figure 4 énumère 4 approches de normalisation différentes, pour un mini-batch d’images $N$ de hauteur $H$ et de largeur $W$, avec des canaux $C$ :

• Batch Normalisation : la normalisation n’est appliquée que sur un canal de l’entrée. C’est la première approche proposée et la plus connue. Nous vous invitons à consulter How to Train Your ResNet 7 : Batch Norm (en anglais) pour plus d’informations.
• Layer norm : la normalisation est appliquée dans une image à travers tous les canaux.
• Instance norm : la normalisation est appliquée sur une seule image et un seul canal.
• Group norm : la normalisation est appliquée sur une seule image mais sur un certain nombre de canaux. Par exemple, le canal 0 à 9 est un groupe, puis le canal 10 à 19 est un autre groupe, et ainsi de suite. En pratique, la taille du groupe est presque toujours de 32. C’est l’approche recommandée par Aaron Defazio, puisqu’elle donne de bons résultats dans la pratique et qu’elle n’est pas en conflit avec la SGD.

Dans la pratique, la normalisation par batch et la normalisation par groupes fonctionnent bien pour les problèmes de vision par ordinateur. La normalisation par couches et la normalisation par instances sont quant à elles fortement utilisées pour les problèmes de langage.

Pourquoi la normalisation est-elle utile ?

Bien que la normalisation fonctionne bien dans la pratique, les raisons de son efficacité sont encore contestées. À l’origine, la normalisation est proposée pour réduire le déplacement interne des covariables, mais certains chercheurs ont prouvé qu’elle était erronée lors d’expériences. Néanmoins, la normalisation présente clairement une combinaison des facteurs suivants :

• Les réseaux comportant des couches de normalisation sont plus faciles à optimiser, ce qui permet d’utiliser des taux d’apprentissage plus importants. La normalisation a un effet d’optimisation qui accélère l’entraînement des réseaux neuronaux.
• Les estimations de la moyenne/écart-type sont bruyantes en raison du caractère aléatoire des échantillons en batch. Ce « bruit » supplémentaire entraîne une meilleure généralisation dans certains cas. La normalisation a un effet de régularisation.
• La normalisation réduit la sensibilité à l’initialisation du poids.

Par conséquent, la normalisation permet d’être plus négligent au sens qu’il est possible de combiner presque tous les blocs constitutifs d’un réseau de neurones et avoir de bonnes chances de l’entraîner sans avoir à considérer son mauvais conditionnement.

Considérations pratiques

Il est important que la rétropropagation se fasse par le calcul de la moyenne et des écarts-types ainsi que par l’application de la normalisation. Sinon l’entraînement du réseau diverge. Le calcul de la rétropropagation est assez difficile et sujet à erreur mais PyTorch est capable de le calculer automatiquement pour nous, ce qui est très utile. Deux classes de couches de normalisation dans PyTorch sont énumérées ci-dessous :

torch.nn.BatchNorm2d(num_features, ...)
torch.nn.GroupNorm(num_groups, num_channels, ...)

La normalisation par batchs a été la première méthode développée et est la plus connue. Cependant, Aaron Defazio recommande d’utiliser plutôt la normalisation par groupes. Elle est plus stable, théoriquement plus simple, et fonctionne généralement mieux. La taille de groupe 32 est une bonne valeur par défaut.

Notez que pour la normalisation par batchs et la normalisation par instances, la moyenne/l’écart-type utilisé est fixé après l’entraînement plutôt que recalculé à chaque fois que le réseau est évalué. En effet de multiples échantillons d’entraînement sont nécessaires pour effectuer la normalisation. Cela n’est pas nécessaire pour la normalisation par groupes et la normalisation par couches, puisque leur normalisation ne porte que sur un seul échantillon d’entraînement.

La mort de l’optimisation

Parfois, nous pouvons faire irruption dans un domaine que nous ne connaissons pas et améliorer la façon dont les choses sont mises en œuvre. L’utilisation de réseaux neuronaux profonds dans le domaine de l’imagerie par résonance magnétique (IRM) pour accélérer la reconstruction des images IRM en est un exemple.

Figure 5 : Parfois, ça marche vraiment !

Reconstruction d’une IRM

Dans le problème traditionnel de la reconstruction d’une IRM, les données brutes sont extraites d’un appareil IRM et une image est reconstruite à partir de celles-ci à l’aide d’un simple algorithme. Les machines d’IRM capturent les données dans un domaine de Fourier en deux dimensions, une ligne ou une colonne à la fois (toutes les quelques millisecondes). Cette entrée brute est composée d’un canal de fréquence et d’un canal de phase et la valeur représente l’amplitude d’une onde sinusoïdale avec cette fréquence et cette phase particulières. En termes simples, on peut considérer qu’il s’agit d’une image de valeur complexe, ayant un canal réel et un canal imaginaire. Si nous appliquons une transformée de Fourier inverse sur cette entrée, c’est-à-dire si nous additionnons toutes ces ondes sinusoïdales pondérées par leurs valeurs, nous pouvons obtenir l’image anatomique originale.

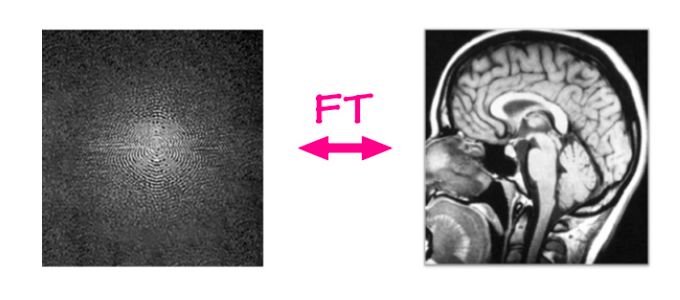
Figure 6 : Reconstruction d’une IRM

Une association linéaire existe pour passer du domaine de Fourier au domaine de l’image. Elle est très efficace, prenant littéralement des millisecondes, quelle que soit la taille de l’image. Mais la question est de savoir si nous pouvons le faire encore plus rapidement.

IRM accélérée

Le nouveau problème qui doit être résolu est l’accélération de l’IRM, où nous entendons rendre le processus de reconstruction de l’IRM beaucoup plus rapide. Nous voulons faire fonctionner les machines plus rapidement tout en étant capables de produire des images de qualité identique. Une façon d’y parvenir, et la plus efficace jusqu’à présent, est de ne pas capturer toutes les colonnes de l’IRM. Nous pouvons sauter certaines colonnes de manière aléatoire, bien qu’il soit utile en pratique de capturer les colonnes du milieu car elles contiennent beaucoup d’informations sur l’ensemble de l’image. Le problème est que nous ne pouvons plus utiliser notre association linéaire pour reconstruire l’image. L’image la plus à droite de la figure 7 montre le résultat d’une association linéaire appliquée à l’espace de Fourier sous-échantillonné. Il est clair que cette méthode ne nous donne pas de résultats très utiles, et qu’il est possible de faire quelque chose d’un peu plus intelligent.

Figure 7 : Association linéaire sur un espace de Fourier sous-échantillonné

Détection comprimée

L’une des plus grandes percées en mathématiques théoriques est la détection comprimée. Un article de Candes et al. a montré que théoriquement, nous pouvons obtenir une reconstruction parfaite à partir de l’image du domaine de Fourier sous-échantillonnée. En d’autres termes, lorsque le signal que nous essayons de reconstruire est épars ou peu structuré, il est alors possible de le reconstruire parfaitement à partir de moins de mesures. Mais pour que cela fonctionne, il y a certaines conditions pratiques à remplir : nous n’avons pas besoin d’échantillonner au hasard mais plutôt d’échantillonner de manière incohérente, bien qu’en pratique, les gens finissent par échantillonner au hasard. En outre, il faut le même temps pour échantillonner une colonne entière ou une demi-colonne, donc en pratique nous échantillonnons aussi des colonnes entières.

Une autre condition est que nous devons avoir une éparsité dans notre image, où par éparsité nous voulons dire beaucoup de zéros ou de pixels noirs dans l’image. L’entrée brute peut être représentée de façon éparse si nous effectuons une décomposition en longueur d’onde. Cependant même cette décomposition nous donne une image approximativement éparse et pas exactement éparse. Ainsi, cette approche nous donne une reconstruction assez bonne mais pas parfaite, comme nous pouvons le voir sur la figure 8. Si l’entrée était très éparse dans le domaine des longueurs d’onde, alors nous obtiendrions certainement une image parfaite.

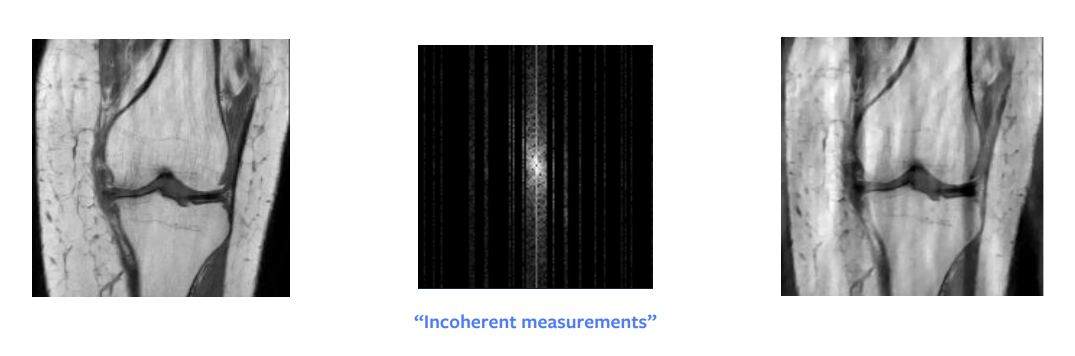
Figure 8 : Détection comprimée

La détection comprimée est basée sur la théorie de l’optimisation. La façon dont nous pouvons obtenir cette reconstruction est de résoudre un mini-problème d’optimisation qui a un terme de régularisation supplémentaire :

où $M$ est la fonction de masque qui met à zéro les entrées non échantillonnées, $\mathcal{F}$ est la transformée de Fourier, $y$ est la donnée observée du domaine de Fourier, $\lambda$ est la force de la pénalité de régularisation et $V$ est la fonction de régularisation.

Le problème d’optimisation doit être résolu pour chaque pas de temps ou chaque « tranche » d’un examen IRM, qui prend souvent beaucoup plus de temps que l’examen lui-même. Cela nous donne une raison supplémentaire de trouver quelque chose de mieux.

Qui a besoin d’une optimisation ?

Au lieu de résoudre le petit problème d’optimisation à chaque étape, pourquoi ne pas utiliser un grand réseau de neurones pour produire directement la solution requise ? Nous espérons pouvoir entraîner un réseau de neurones suffisamment complexe pour qu’il résolve le problème d’optimisation en une seule étape et produise un résultat aussi bon que la solution obtenue en résolvant le problème d’optimisation à chaque étape temporelle.

où $B$ est notre modèle d’apprentissage profond et $y$ est la donnée observée dans le domaine de Fourier.

Il y a 15 ans, cette approche était difficile mais est aujourd’hui beaucoup plus facile à mettre en œuvre. La figure 9 montre le résultat d’une approche d’apprentissage profond au problème. Nous pouvons voir qu’il est bien meilleur que l’approche de détection comprimée et ressemble beaucoup au scanner réel.

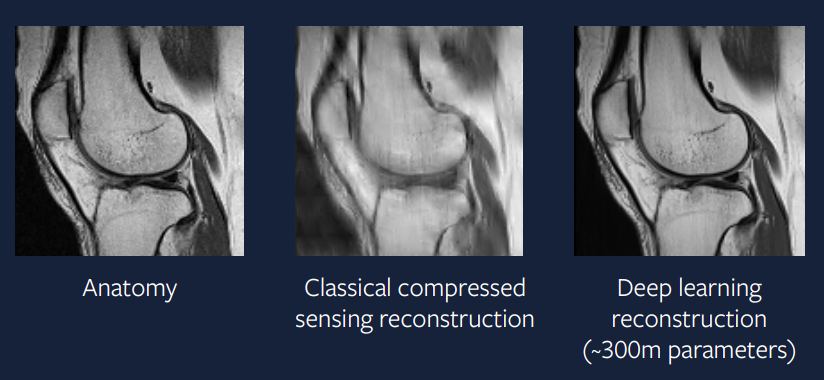
Figure 9 : Apprentissage profond

Le modèle utilisé pour générer cette reconstruction fait appel à un optimiseur ADAM, à des couches de normalisation par groupes et à un ConvNet basé sur U-Net.