Prediction et apprentissage d'une politique sous incertitude

Introduction et configuration du problème

Disons que nous voulons apprendre à conduire dans un modèle d’apprentissage par renforcement (RL pour Reinforcement learning). Nous entraînons des modèles en RL en laissant le modèle faire des erreurs et en apprenant de celles-ci. Mais ce n’est pas la meilleure façon de procéder car les erreurs peuvent nous conduire au paradis ou en enfer où il est inutile d’apprendre.

Parlons donc d’une méthode plus « humaine » pour apprendre à conduire une voiture. Prenons un exemple de changement de voie. En supposant que la voiture roule à 100 km/h, ce qui correspond à peu près à 30 m/s, si nous regardons à 30 m devant nous, nous regardons en gros 1 s dans le futur.

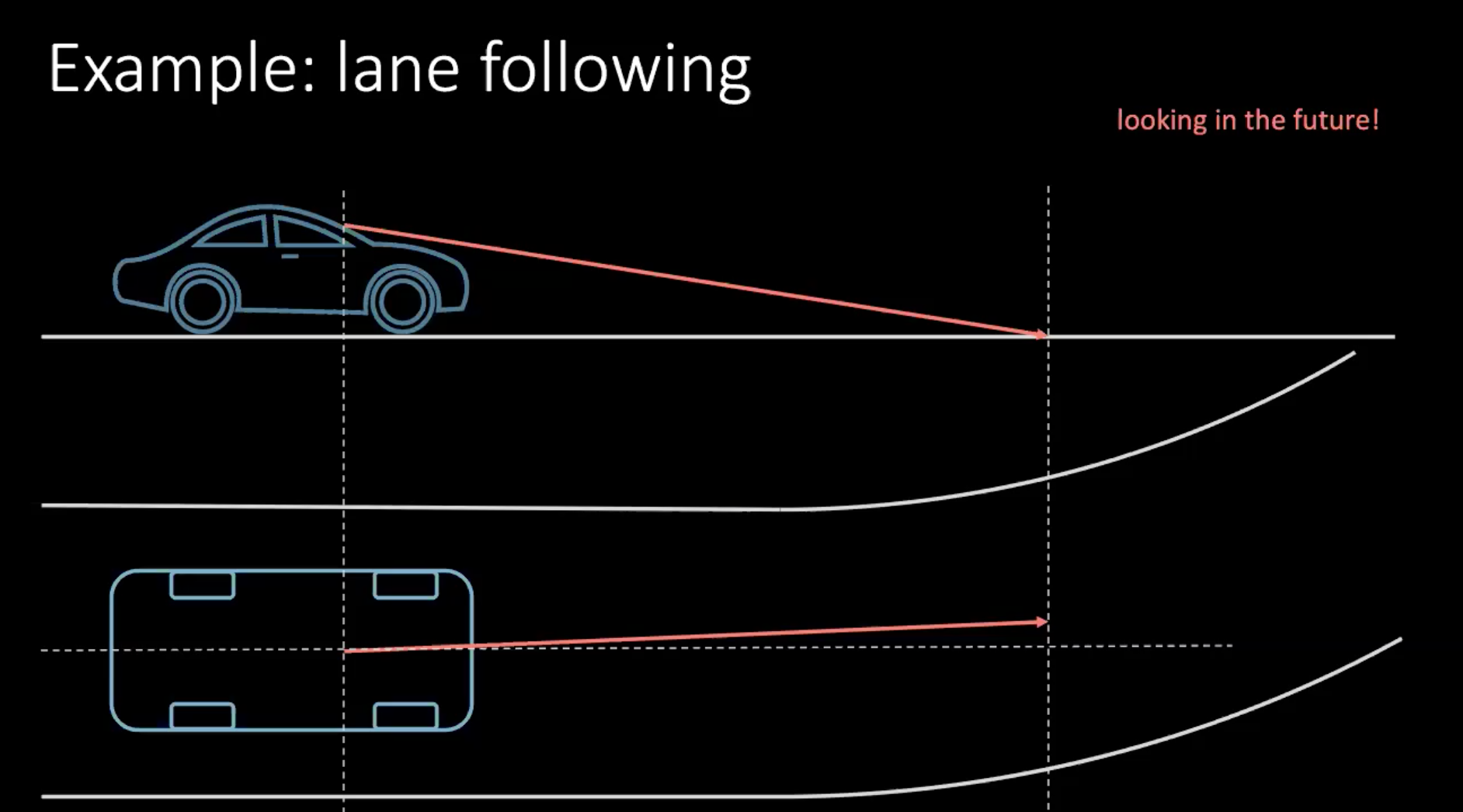
Figure 1 : Regarder vers l'avenir en conduisant

Si nous devons tourner, nous devons prendre une décision en fonction de l’avenir proche. Pour prendre un virage dans quelques mètres, nous prenons une mesure maintenant, qui dans ce contexte est de tourner le volant. Prendre une décision ne dépend pas seulement de notre conduite, mais aussi des véhicules environnants dans la circulation. Comme tout le monde autour de nous n’est pas aussi déterministe, il est très difficile de prendre en compte toutes les possibilités.

Décomposons maintenant ce qui se passe dans ce scénario. Nous avons un agent (représenté ici par un cerveau) qui prend l’entrée $s_t$ (images de la position, de la vitesse et du contexte) et produit une action $a_t$ (contrôle de la direction, accélération et freinage). L’environnement nous amène à un nouvel état et nous renvoie un coût $c_t$.

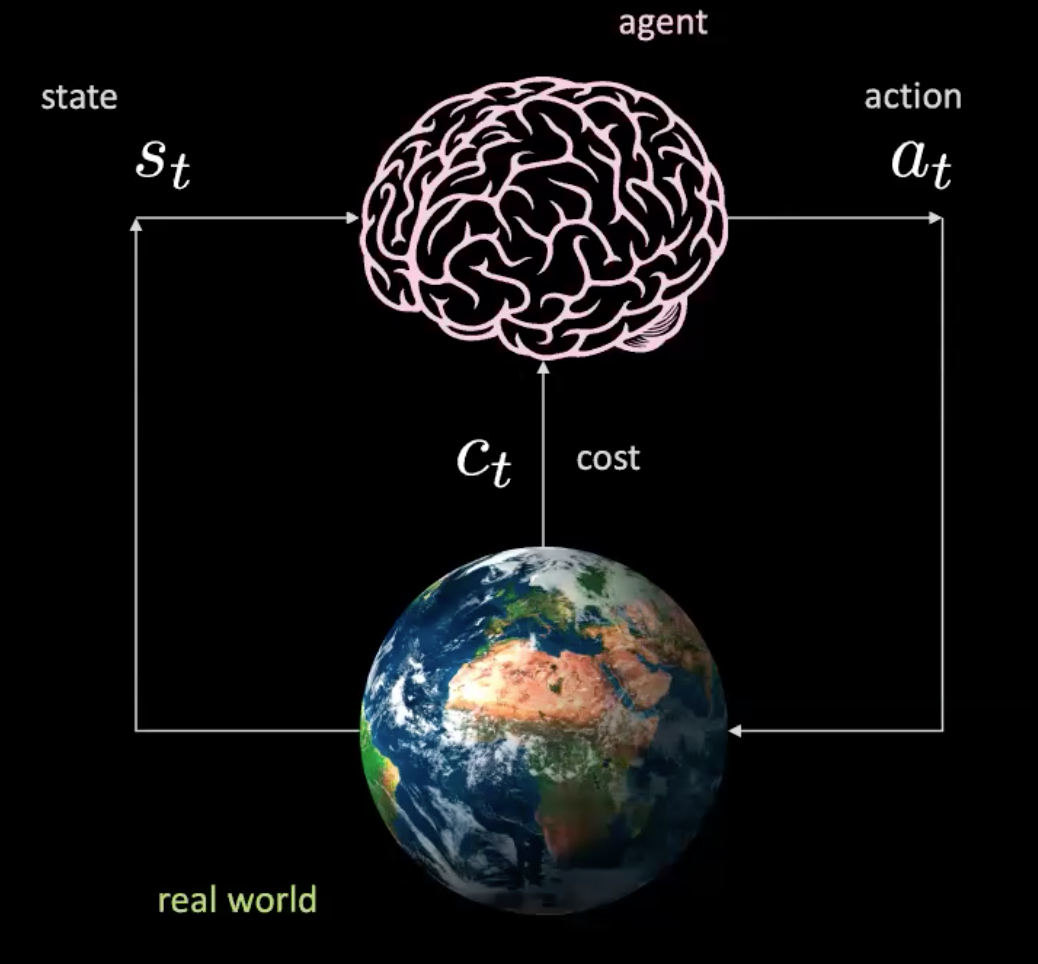
Figure 2 : Illustration d'un agent dans le monde réel

C’est comme un réseau où nous prenons des actions étant donné un état spécifique et où le monde nous donne l’état suivant et la conséquence suivante. C’est un modèle libre, car chaque action nous fait interagir avec le monde réel. Mais pouvons-nous entraîner un agent sans interagir avec le monde réel ?

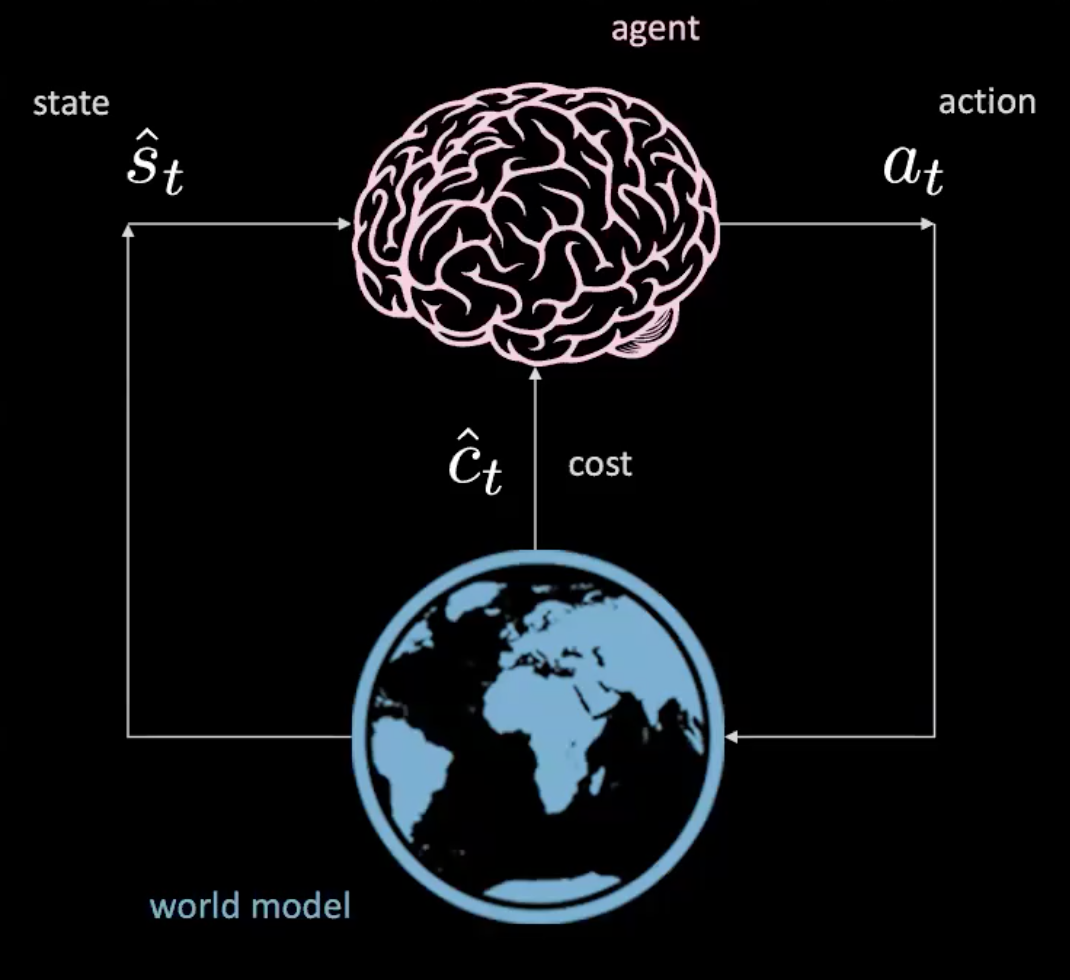
Figure 3 : Illustration d'un agent dans le modèle du monde

Jeu de données

Avant de discuter de la manière d’apprendre le modèle du monde, explorons le jeu de données dont nous disposons. Nous avons 7 caméras montées sur le toit d’un bâtiment de 30 étages qui fait face à une autoroute. Nous ajustons les caméras pour obtenir une vue de haut en bas et extrayons ensuite des boîtes de délimitation pour chaque véhicule. Au temps $t$, nous pouvons déterminer $p_t$ représentant la position, $v_t$ représentant la vitesse et $i_t$ représentant l’état actuel de la circulation autour du véhicule.

Comme nous connaissons les cinématiques de la conduite, nous pouvons les inverser pour déterminer quelles sont les actions que le conducteur effectue. Par exemple, si la voiture se déplace dans un mouvement rectiligne uniforme, nous savons que l’accélération est nulle (ce qui signifie qu’il n’y a pas d’action).

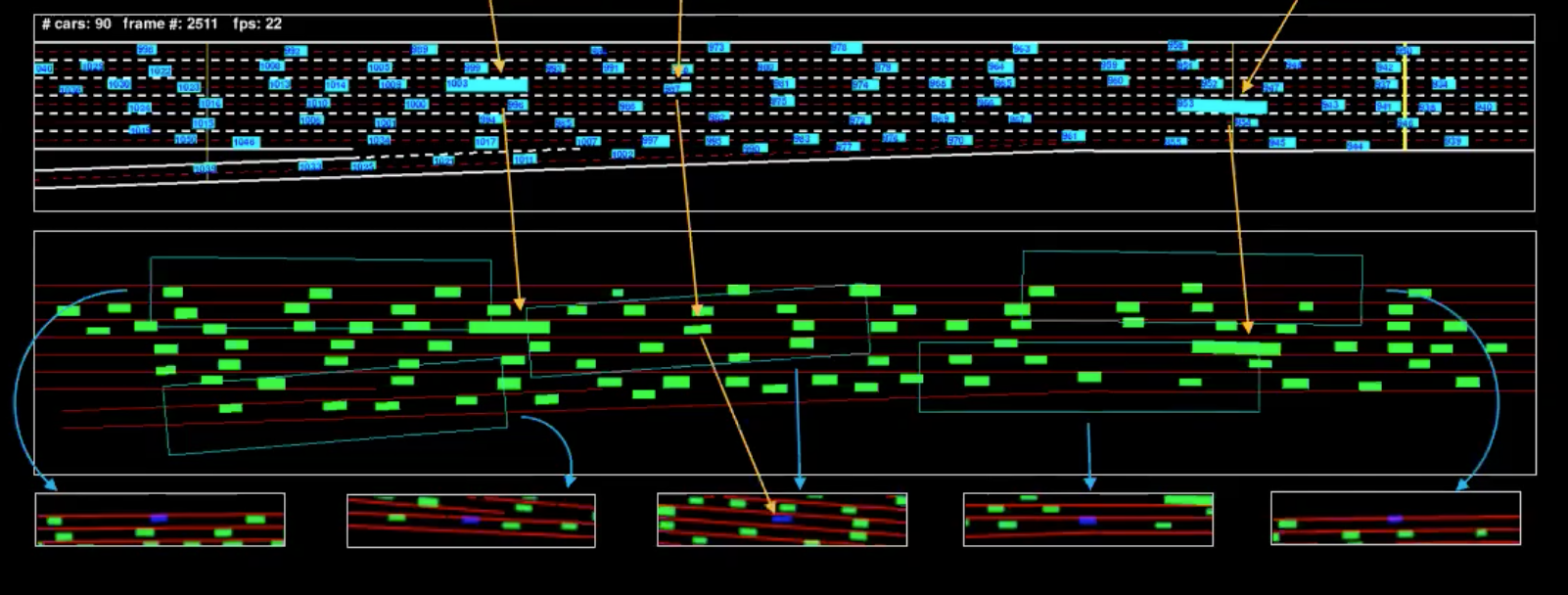
Figure 4 : Représentation mécanique d'une seule image

L’illustration en bleu est le flux et l’illustration en vert est ce que l’on peut appeler la représentation de la machine. Pour mieux comprendre cela, nous avons isolé quelques véhicules (marqués dans l’illustration). Les vues que nous voyons ci-dessus sont les boites délimitant le champ de vision de ces véhicules.

Coût

Il y a deux types de coûts différents ici : le coût de la voie et le coût de proximité. Le coût de la voie nous indique dans quelle mesure nous sommes à l’intérieur d’une voie et le coût de proximité nous indique dans quelle mesure nous sommes proches des autres voitures.

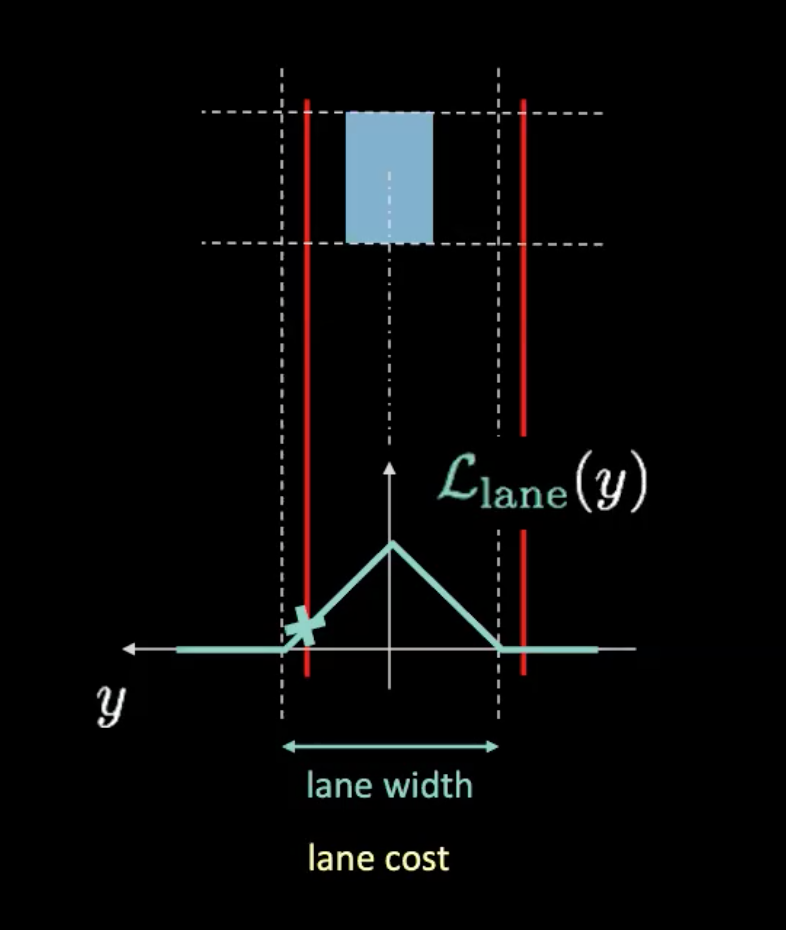
Figure 5 : Coût des voies

Dans la figure ci-dessus, les lignes pointillées représentent les voies réelles et les lignes rouges nous aident à calculer le coût de la voie compte tenu de la position actuelle de notre voiture. Les lignes rouges se déplacent en fonction de la position de notre voiture. La hauteur de l’intersection des lignes rouges avec la courbe potentielle (en cyan) nous donne le coût. Si la voiture est au centre de la voie, les deux lignes rouges se chevauchent avec les voies réelles, ce qui donne un coût nul. D’autre part, lorsque la voiture s’éloigne du centre, les lignes rouges se déplacent également, ce qui entraîne un coût non nul.

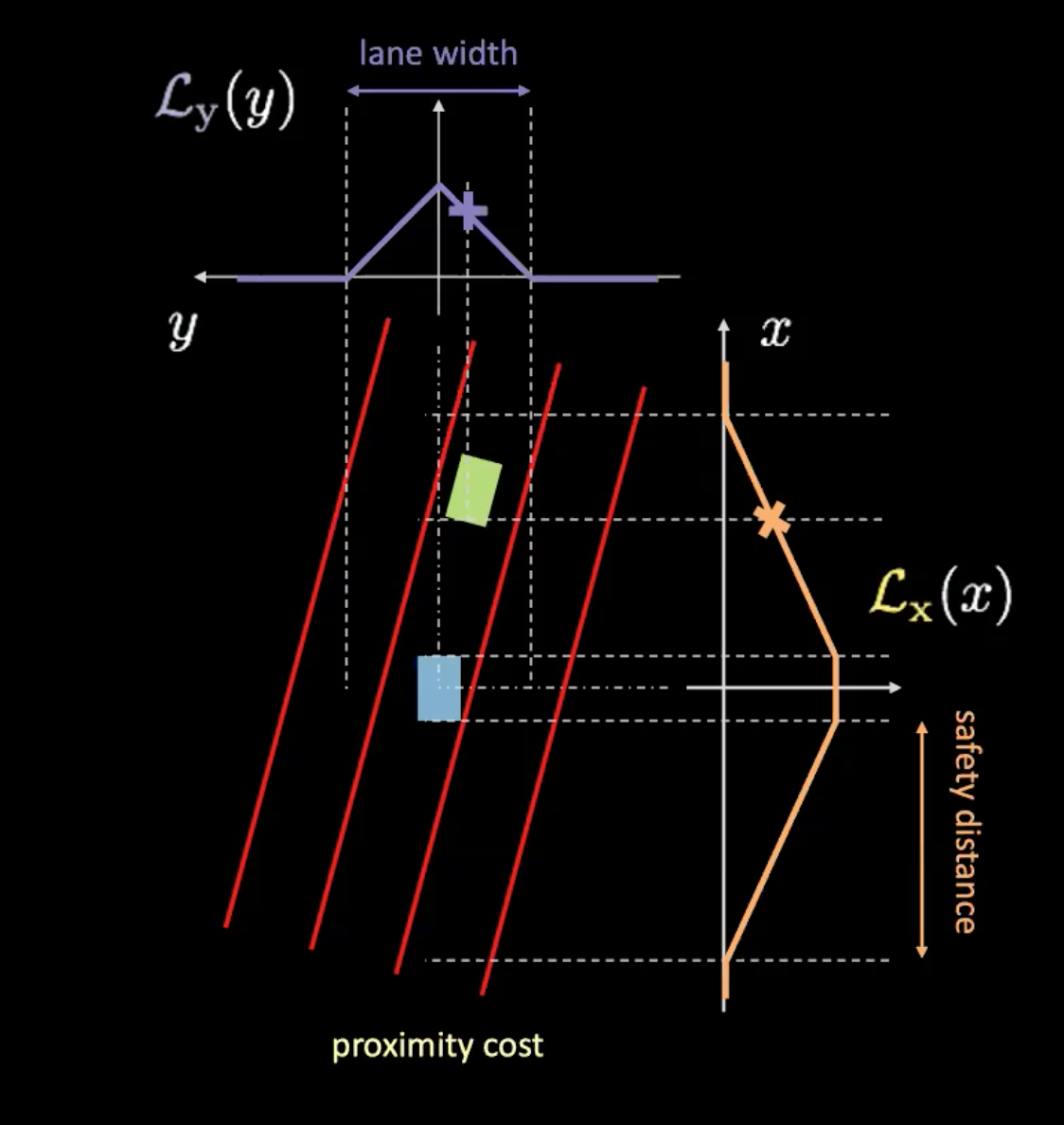
Figure 6 : Coût de proximité

Le coût de proximité a deux composantes ($\mathcal{L}_x$ et $\mathcal{L}_y$). $\mathcal{L}_y$ est similaire au coût de la voie et $\mathcal{L}_x$ dépend de la vitesse de notre voiture. La courbe orange de la figure 6 nous renseigne sur la distance de sécurité. Plus la vitesse de la voiture augmente, plus la courbe orange s’élargit. Plus la voiture roule vite, plus il faut regarder devant et derrière. La hauteur de l’intersection d’une voiture avec la courbe orange détermine $\mathcal{L}_x$.

Le produit de ces deux éléments nous donne le coût de la proximité.

Apprentissage d’un modèle du monde

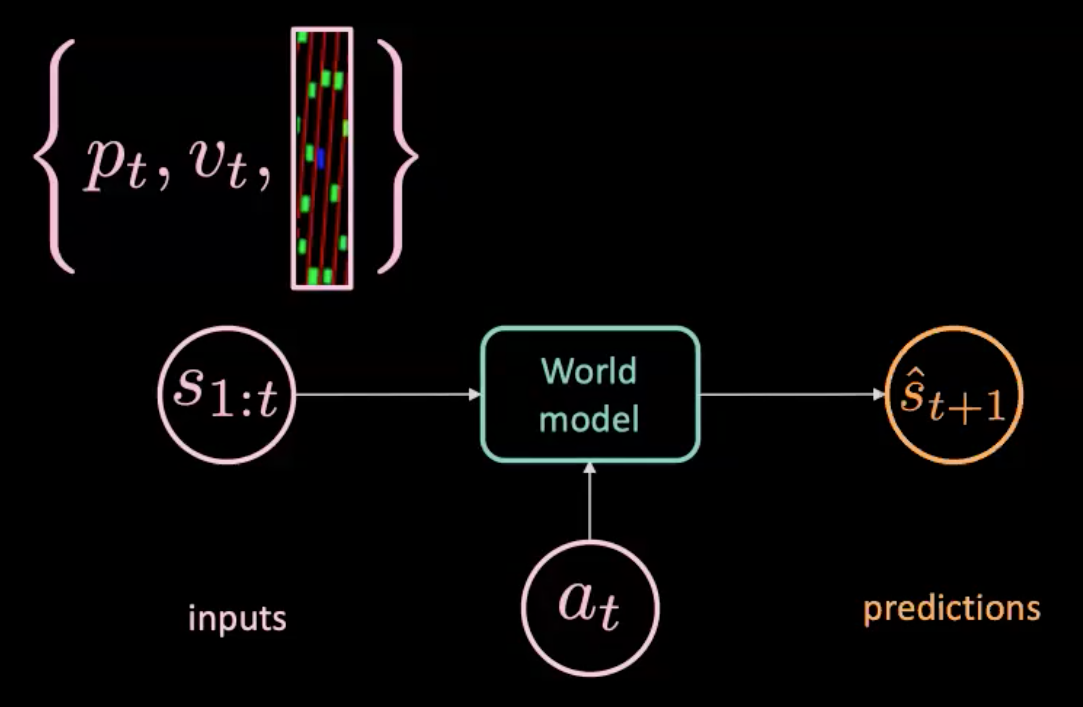
Figure 7 : Illustration d’un modèle du monde

Le modèle du monde est alimenté par une action $a_t$ (direction, freinage et accélération) et $s_{1:t}$ (séquence d’états où chaque état est représenté par des images de position, de vitesse et de contexte à ce temps) et il prédit l’état suivant $\hat s_{t+1}$. D’autre part, nous avons le monde réel qui nous dit ce qui s’est réellement passé ($s_{t+1}$). Nous optimisons la MSE entre la prédiction ($\hat s_{t+1}$) et la cible ($s_{t+1}$) pour entraîner notre modèle.

Prédicteur-décodeur déterministe

L’une des façons d’entraîner notre modèle du monde est d’utiliser un modèle prédicteur-décodeur expliqué ci-dessous.

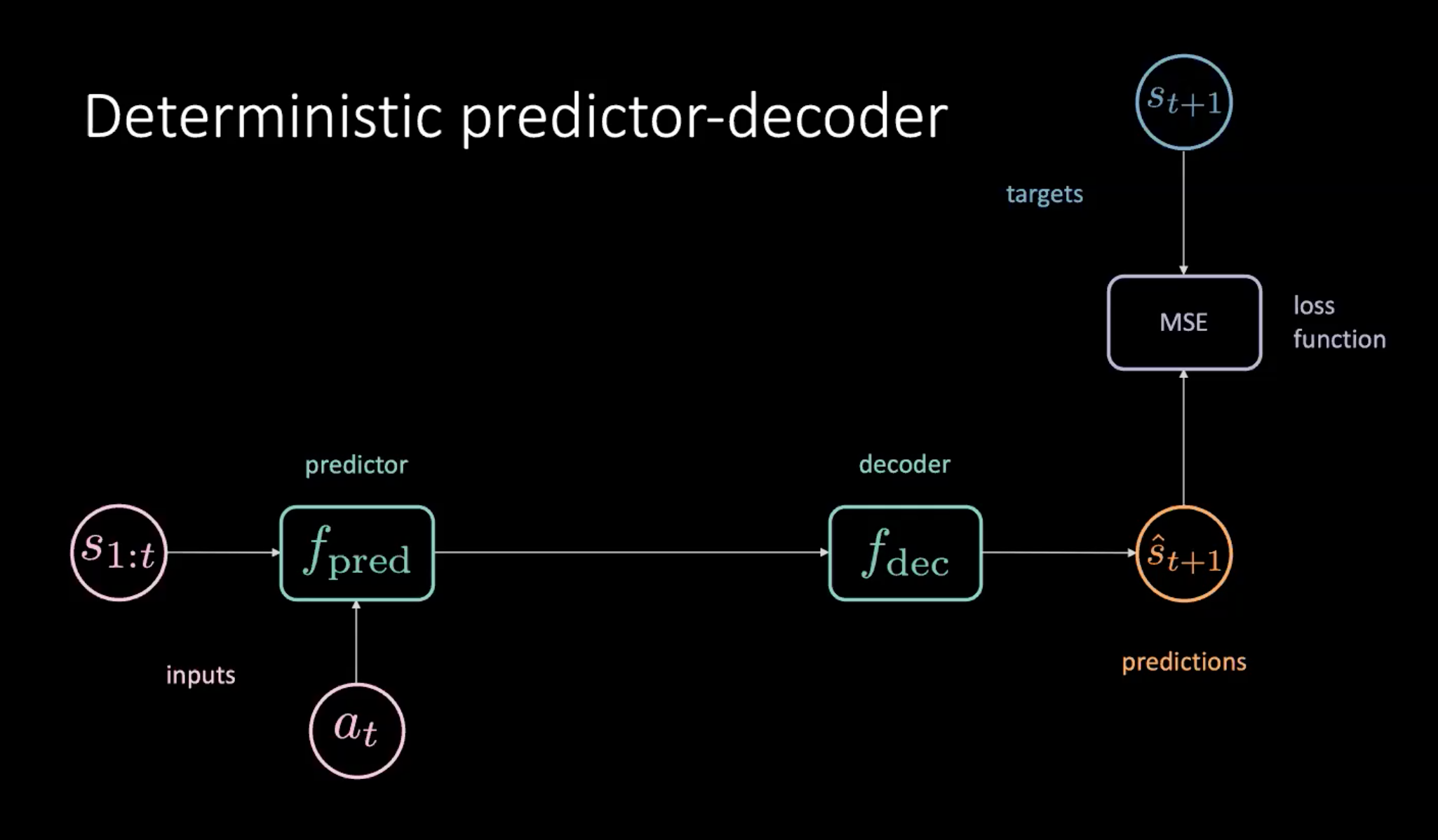
Figure 8 : Prédicteur-décodeur déterministe pour apprendre le modèle du monde

Comme le montre la figure 8, nous avons une séquence d’états ($s_{1:t}$) et d’actions ($a_t$) qui sont fournies au module prédicteur. Le prédicteur produit une représentation cachée de l’avenir qui est transmise au décodeur. Le décodeur décode la représentation cachée du futur et émet une prédiction ($\hat s_{t+1}$). Nous entraînons ensuite notre modèle en minimisant la MSE entre la prédiction $\hat s_{t+1}$ et la cible $s_{t+1}$.

Figure 9 : Avenir réel vs Avenir déterministe

Malheureusement, cela ne fonctionne pas !

Nous constatons que le résultat déterministe devient très flou. C’est parce que notre modèle fait la moyenne de toutes les possibilités futures. Cela peut être comparé à la multimodalité du futur dont nous avons déjà évoqué dans un cours précédent où un stylo placé à l’origine est laché au hasard. Si nous prenons la moyenne de tous les endroits, cela nous donne l’impression que le stylo n’a jamais bougé, ce qui est incorrect.

Nous pouvons résoudre ce problème en introduisant des variables latentes dans notre modèle.

Réseau prédictif variationnel

Pour résoudre le problème énoncé dans la section précédente, nous ajoutons une variable latente de faible dimension $z_t$ au réseau d’origine qui passe par un module d’expansion $f_{exp}$ pour correspondre à la dimensionnalité.

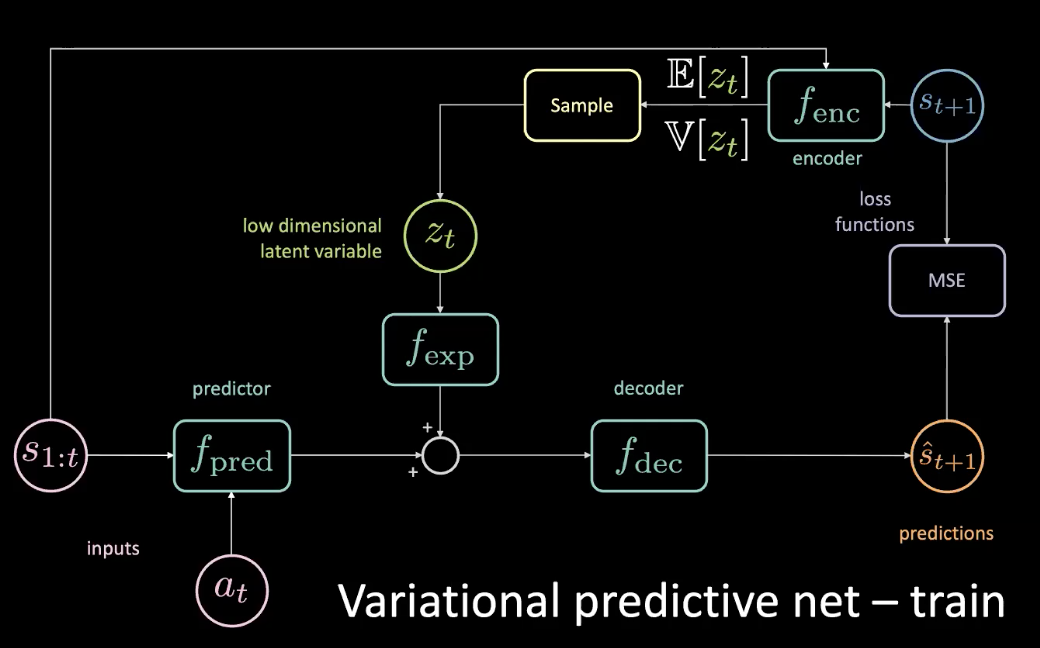
Figure 10 : Réseau prédictif variationnel - entraînement

Le $z_t$ est choisi de telle sorte que la MSE soit minimisée pour une prévision spécifique. En réglant la variable latente, vous pouvez toujours ramener la MSE à zéro en effectuant une descente de gradient dans l’espace latent. Mais c’est très coûteux. Nous pouvons donc réellement prédire cette variable latente en utilisant un encodeur. L’encodeur prend l’état futur pour nous donner une distribution avec une moyenne et une variance à partir de laquelle nous pouvons échantillonner $z_t$.

Pendant l’entraînement, nous pouvons découvrir ce qui se passe en regardant dans le futur et en en tirant des informations et utiliser ces informations pour prédire la variable latente. Cependant, nous n’avons pas accès à l’avenir pendant la durée des tests. Nous réglons ce problème en appliquant l’encodeur pour obtenir une distribution postérieure aussi proche que possible de la distribution antérieure en optimisant la divergence KL.

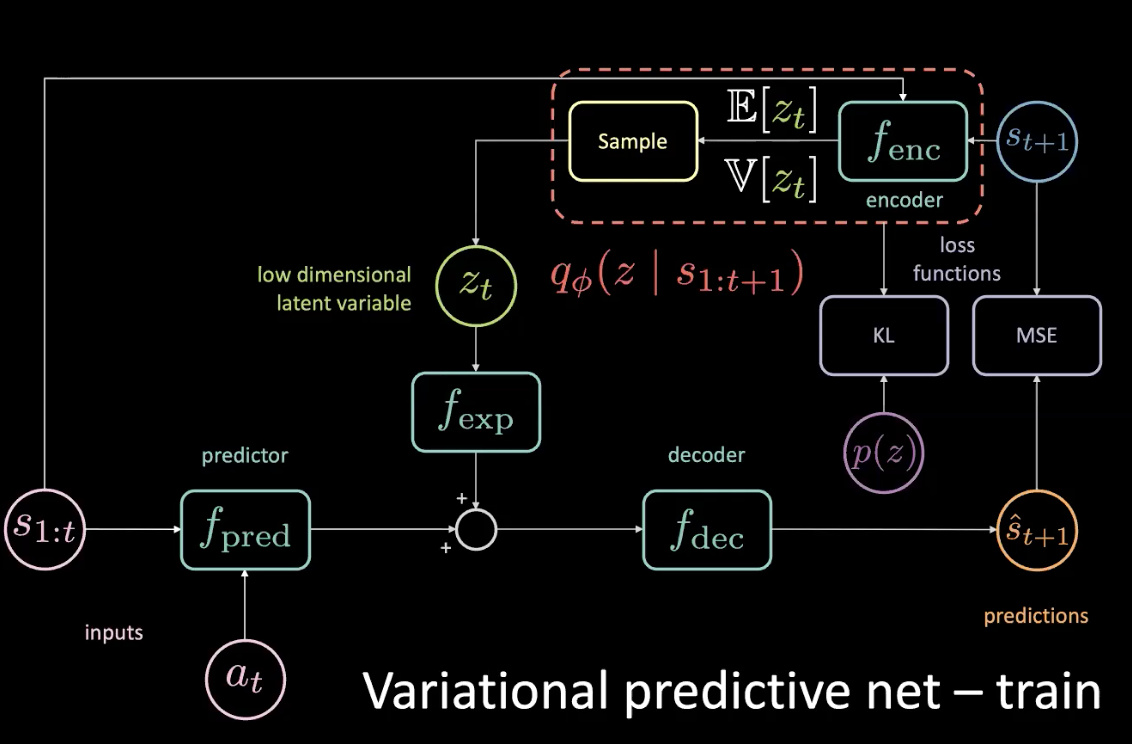
Figure 11 : Réseau prédictif variationnel - entraînement (avec distribution préalable)

Maintenant, examinons l’inférence. Comment conduisons-nous ?

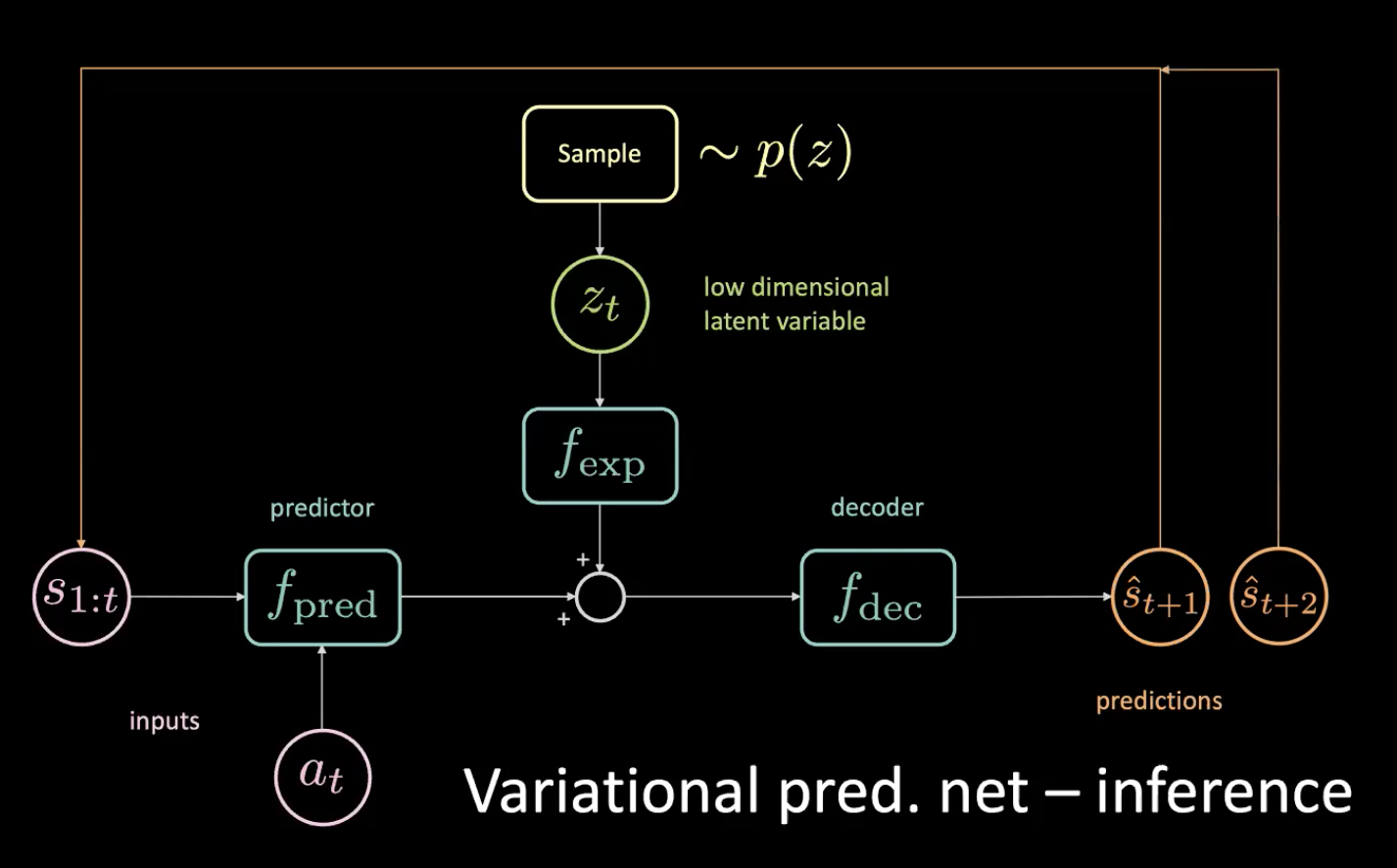
Figure 12 : Réseau prédictif variationnel - inférence

Nous échantillonnons la variable latente de faible dimension $z_t$ de la précédente en forçant l’encodeur à la tirer vers cette distribution. Après avoir obtenu la prédiction $\hat s_{t+1}$, nous la remettons (dans une étape autorégressive) et obtenons la prédiction suivante $\hat s_{t+2}$ et continuons à alimenter le réseau de cette façon.

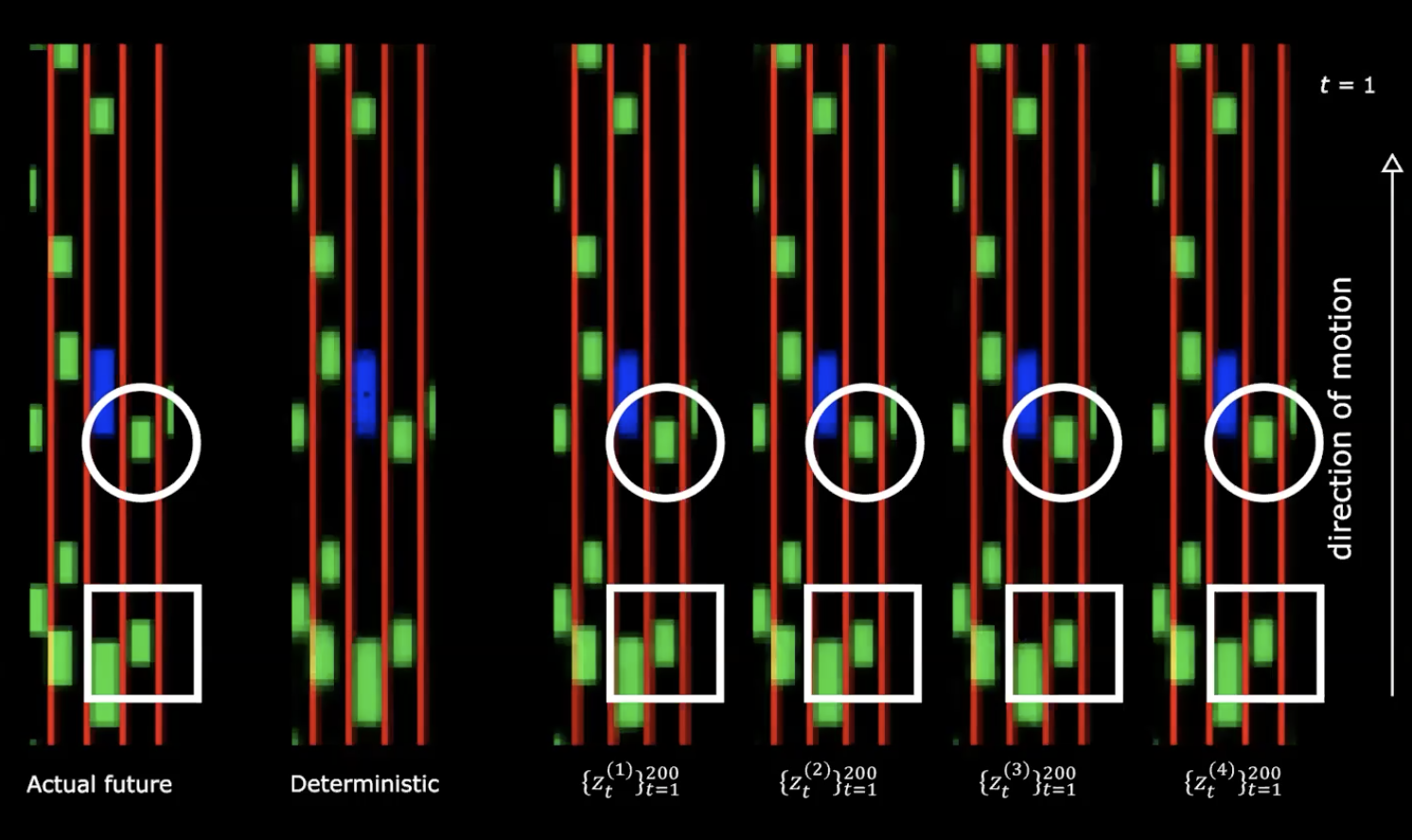
Figure 13 : Avenir réel vs Déterministe

Dans la partie droite de la figure ci-dessus, on peut voir quatre tirages différents de la distribution normale. Nous partons du même état initial et fournissons 200 valeurs différentes à la variable latente.

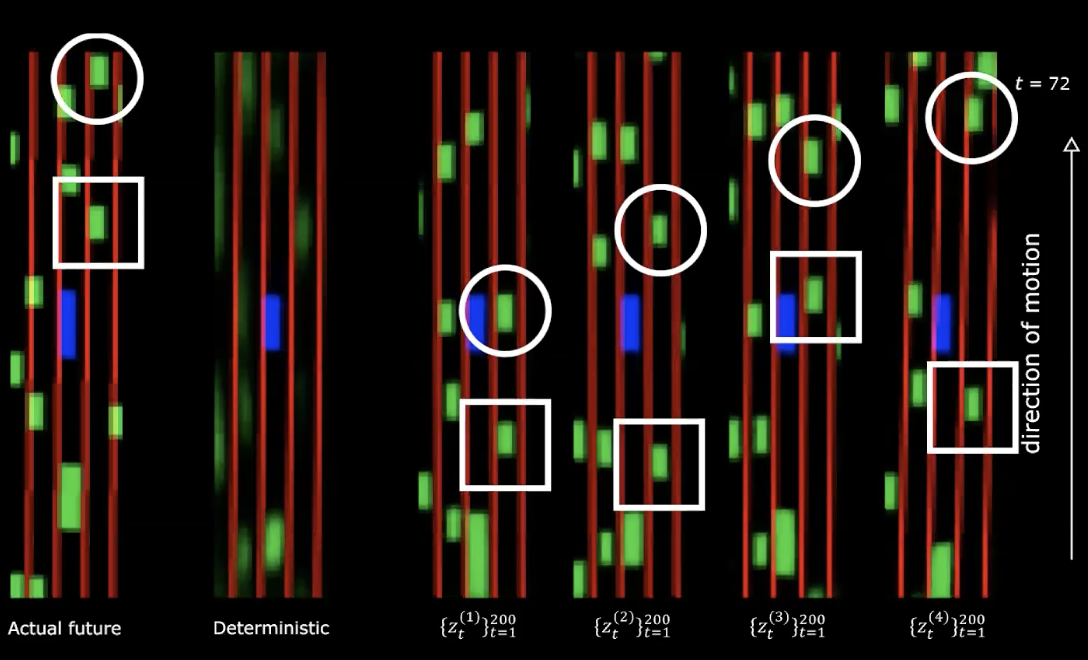
Figure 14 : Avenir réel vs Déterministe - après mouvement

Nous pouvons remarquer que le fait de fournir différentes variables latentes génère différentes séquences d’états avec différents comportements. Ce qui signifie que nous disposons d’un réseau qui génère le futur.

Quelle est la prochaine étape ?

Nous pouvons maintenant utiliser cette énorme quantité de données pour entraîner notre politique en optimisant les coûts de voies et de proximité décrits ci-dessus.

Ces futurs multiples proviennent de la séquence de variables latentes que l’on donne au réseau. Si nous effectuons une montée de gradient dans l’espace latent, nous essayons d’augmenter le coût de proximité afin d’obtenir la séquence de variables latentes de sorte que les autres voitures vont nous foncer dessus.

Insensibilité à l’action et dropout latent

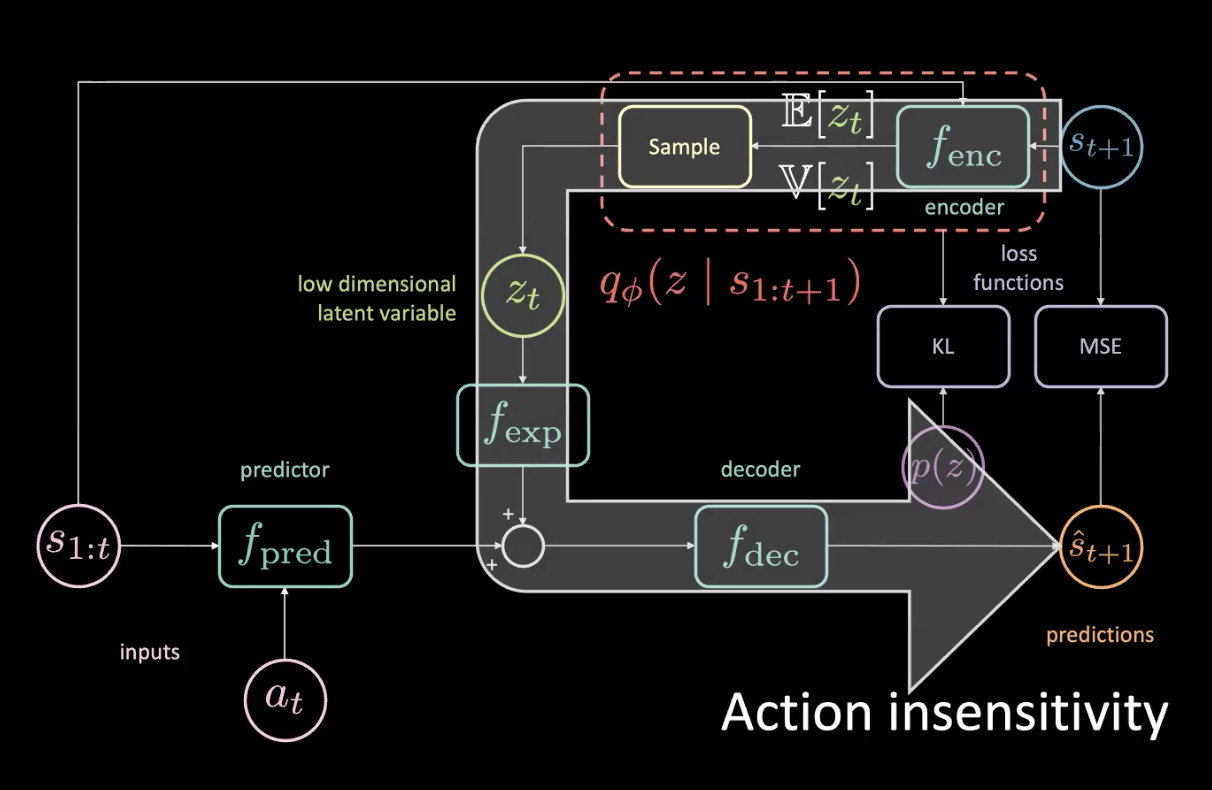
Figure 15 : Problèmes - Insensibilité à l'action

Étant donné que nous avons réellement accès à l’avenir, si nous tournons à gauche, même légèrement, tout va tourner à droite et cela va contribuer de façon énorme à la MSE. La perte MSE peut être minimisée si la variable latente peut informer la partie inférieure du réseau que tout va tourner à droite, ce qui n’est pas ce que nous voulons ! Nous pouvons dire quand tout tourne à droite puisque c’est une tâche déterministe.

La grande flèche de la figure 15 signifie une fuite d’informations et donc n’est pas plus sensible à l’action en cours fournie au prédicteur.

Figure 16 : Problème - Insensibilité à l'action

Dans la figure 16, dans le diagramme le plus à droite, nous avons la séquence réelle des variables latentes (les variables latentes qui nous permettent d’obtenir le futur le plus précis) et nous avons la séquence réelle des actions prises par l’expert. Les deux figures à gauche de celle-ci ont un échantillon aléatoire de variables latentes mais la séquence réelle d’actions, donc nous nous attendons à voir le pilotage. La dernière à gauche a la séquence réelle des variables latentes, mais des actions arbitraires, et nous pouvons clairement voir que la rotation provient principalement de la variable latente plutôt que de l’action, ce qui encode la rotation et l’action (qui sont échantillonnées à partir d’autres épisodes).

Comment résoudre ce problème ?

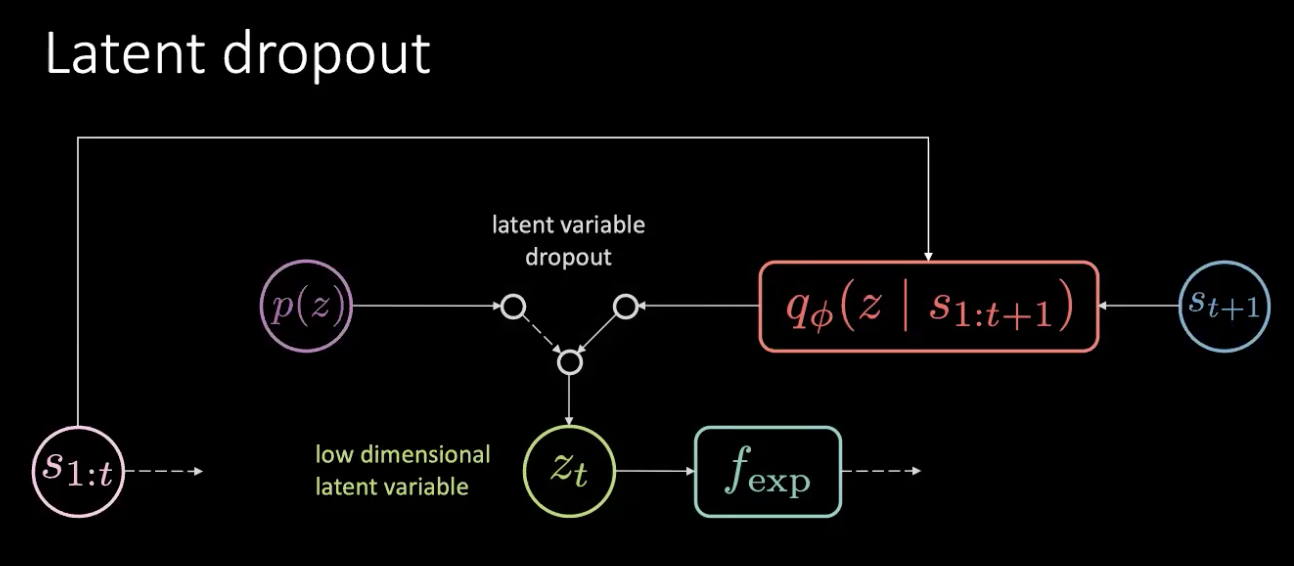
Figure 17 : Correction - Dropout latent

Le problème n’est pas une fuite de mémoire mais une fuite d’informations. Nous réglons ce problème en éliminant simplement cette latente et en la prélevant au hasard dans la distribution antérieure. Nous ne nous appuyons pas toujours sur la sortie de l’encodeur ($f_{enc}$) mais nous prélevons dans la distribution antérieure. De cette façon, nous ne pouvons plus encoder la rotation dans la variable latente. Ainsi l’information est encodée dans l’action plutôt que dans la variable latente.

Figure 18 : Performance avec dropout latent

Sur les deux dernières images de droite, on voit deux ensembles différents de variables latentes ayant une séquence réelle d’actions et ces réseaux ont été entraînés avec l’astuce du dropout latent. Nous pouvons maintenant voir que la rotation est maintenant codée par l’action et non plus par les variables latentes.

Entraînement de l’agent

Dans les sections précédentes, nous avons vu comment nous pouvons obtenir un modèle du monde en simulant des expériences réelles. Dans cette section, nous utilisons ce modèle du monde pour l’entraînement de notre agent. Notre objectif est d’apprendre la politique à suivre pour agir, compte tenu de l’histoire des états précédents. Étant donné un état $s_t$ (vitesse, position et images de contexte), l’agent entreprend une action $a_t$ (accélération, freinage et direction), le modèle du monde produit un état suivant et le coût associé à cette paire $(s_t, a_t)$ qui est une combinaison du coût de proximité et du coût de la voie.

Comme nous l’avons vu dans la section précédente, pour éviter des prédictions floues, nous devons échantillonner la variable latente $z_t$ du module encodeur de l’état futur $s_{t+1}$ ou de la distribution antérieure $P(z)$. Le modèle du monde obtient les états précédents $s_{1:t}$, les mesures prises par notre agent et la variable latente $z_t$ pour prédire l’état suivant $\hat s_{t+1}$ et le coût. Cela constitue un module qui est reproduit plusieurs fois (figure 19) pour nous donner la prédiction finale et la perte à optimiser.

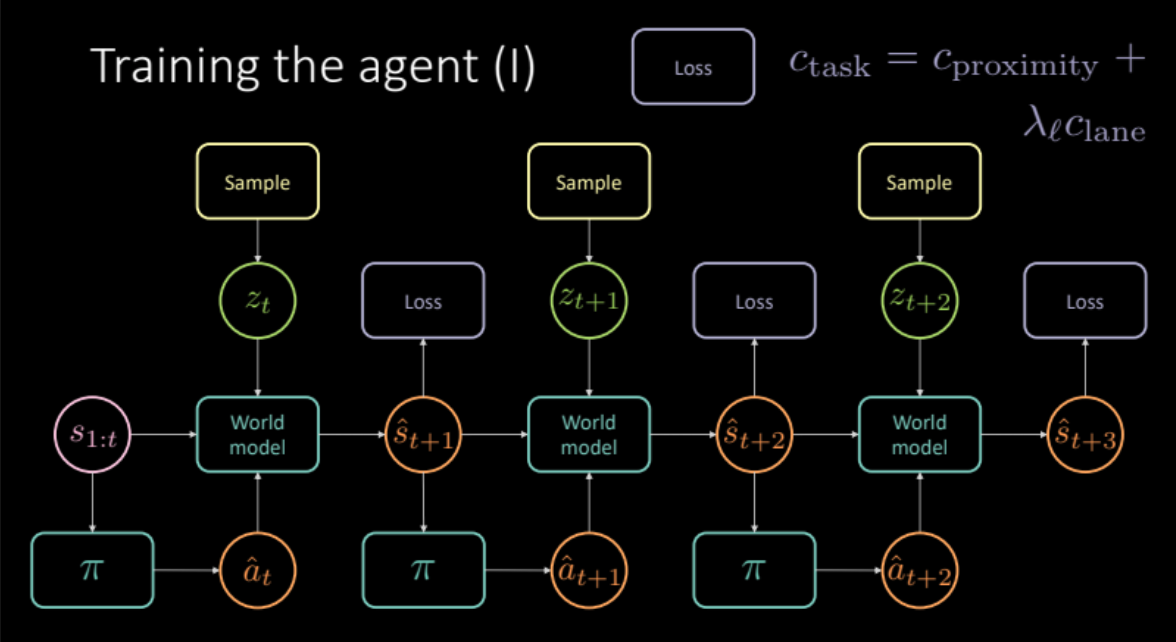
Figure 19 : Architecture du modèle spécifique à la tâche

Notre modèle est prêt, voyons de quoi il a l’air.

Figure 20 : Politique apprise : l'agent entre en collision ou s'éloigne de la route

Malheureusement, cela ne fonctionne pas. La politique entraînée de cette façon n’est pas utile car elle apprend à prédire tout le noir puisqu’il en résulte un coût nul.

Comment pouvons-nous résoudre ce problème ? Pouvons-nous essayer d’imiter d’autres véhicules pour améliorer nos prévisions ?

Imiter l’expert

Comment imiter les experts ici ? Nous voulons que la prédiction de notre modèle après une action particulière d’un état soit aussi proche que possible de l’avenir réel. Cela agit comme un régulariseur expert pour notre entraînement. Notre fonction de coût comprend maintenant à la fois le coût spécifique de la tâche (coût de proximité et coût de la voie) et ce terme de régulariseur expert. Maintenant que nous calculons également la perte par rapport à l’avenir réel, nous devons supprimer la variable latente du modèle parce qu’elle nous donne une prédiction spécifique, mais ce paramètre fonctionne mieux si nous travaillons uniquement avec la prédiction moyenne.

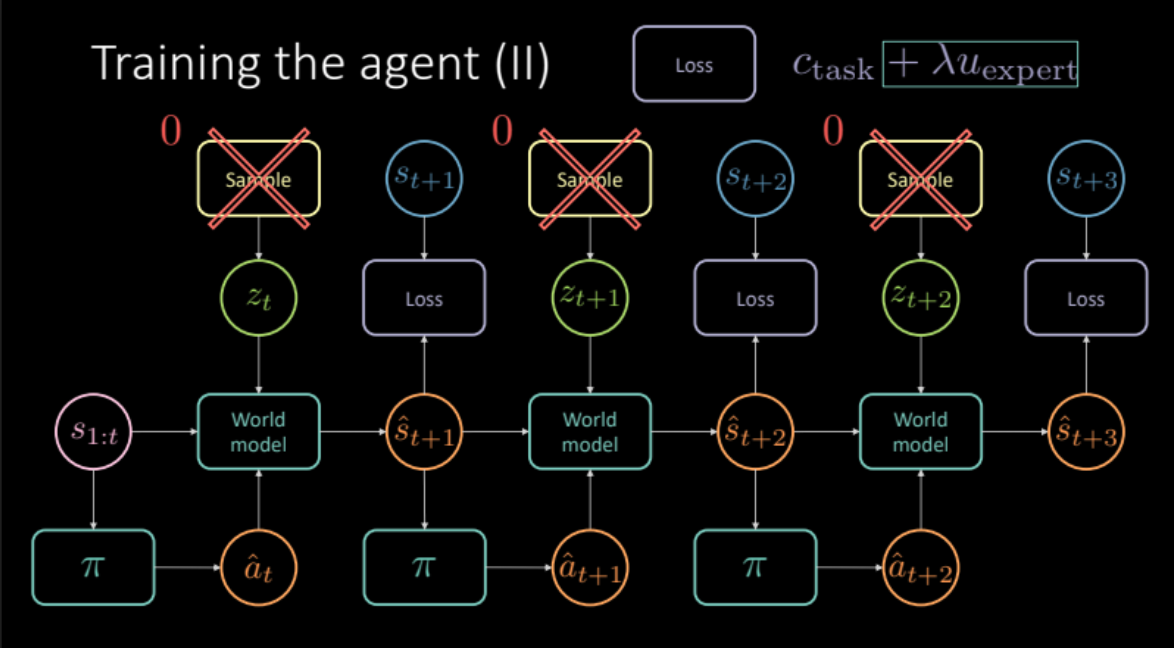
Figure 21 : Architecture de modèle basée sur la régularisation expert

Comment ce modèle fonctionne-t-il ?

Figure 22 : Politique apprise en imitant les experts

Comme nous pouvons le voir dans la figure ci-dessus, le modèle fonctionne en fait incroyablement bien et apprend à faire de très bonnes prédictions. C’était un apprentissage par imitation basé sur le modèle, nous avons essayé de modeler notre agent pour essayer d’imiter les autres.

Mais pouvons-nous faire mieux ? Avons-nous simplement entraîné l’auto-encodeur variationnel pour le supprimer à la fin ?

Il s’avère que nous pouvons encore améliorer les résultats si nous cherchons à minimiser l’incertitude des prédictions du modèle prédictif.

Minimiser l’incertitude du modèle prédictif

Qu’entendons-nous par réduire au minimum l’incertitude des modèles de prédiction et comment le faire ? Avant de répondre à cette question, récapitulons ce que nous avons vu au cours de la troisième semaine.

Si nous entraînons plusieurs modèles sur les mêmes données, tous ces modèles s’accordent sur les points de la région d’entraînement (indiquée en rouge), ce qui donne une variance nulle dans la région d’entraînement. Mais plus nous nous éloignons de la région d’entraînement, plus les trajectoires des fonctions de perte de ces modèles commencent à diverger et plus la variance augmente. Ceci est illustré par la figure 23. Mais comme la variance est différentiable, nous pouvons effectuer une descente de gradient sur la variance afin de la minimiser.

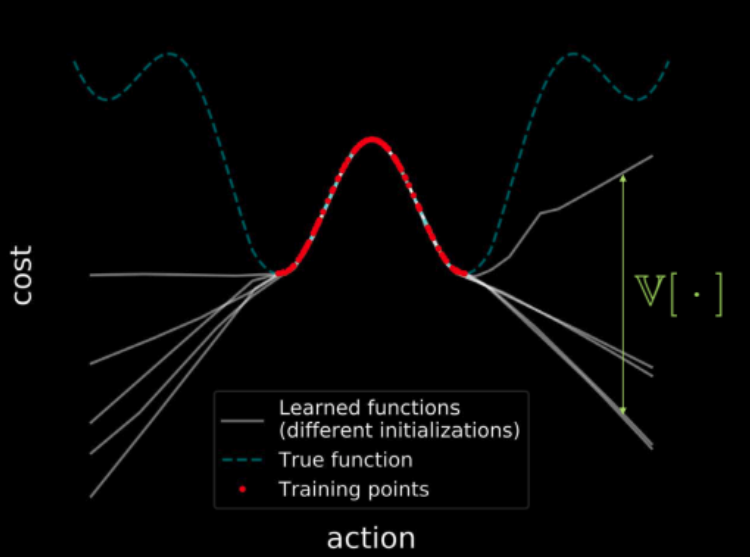
Figure 23 : Visualisation des coûts sur l'ensemble de l'espace d'entrée

Pour en revenir à notre discussion, nous constatons que l’apprentissage d’une politique uniquement à l’aide de données d’observation est difficile car la distribution des états qu’elle produit au moment de l’exécution peut différer de ce qui a été observé pendant la phase d’entraînement. Le modèle du monde peut faire des prédictions arbitraires en dehors du domaine sur lequel il a été entraîné, ce qui peut entraîner des coûts peu élevés. Le réseau politique peut alors exploiter ces erreurs dans le modèle dynamique et produire des actions qui conduisent à des états faussement optimistes.

Pour y remédier, nous proposons un coût supplémentaire qui mesure l’incertitude du modèle dynamique sur ses propres prédictions. Ce coût peut être calculé en faisant passer la même entrée et la même action par plusieurs masques de dropout différents, et en calculant la variance entre les différentes sorties. Cela encourage le réseau politique à ne produire que des actions pour lesquelles le modèle de prospective est confiant.

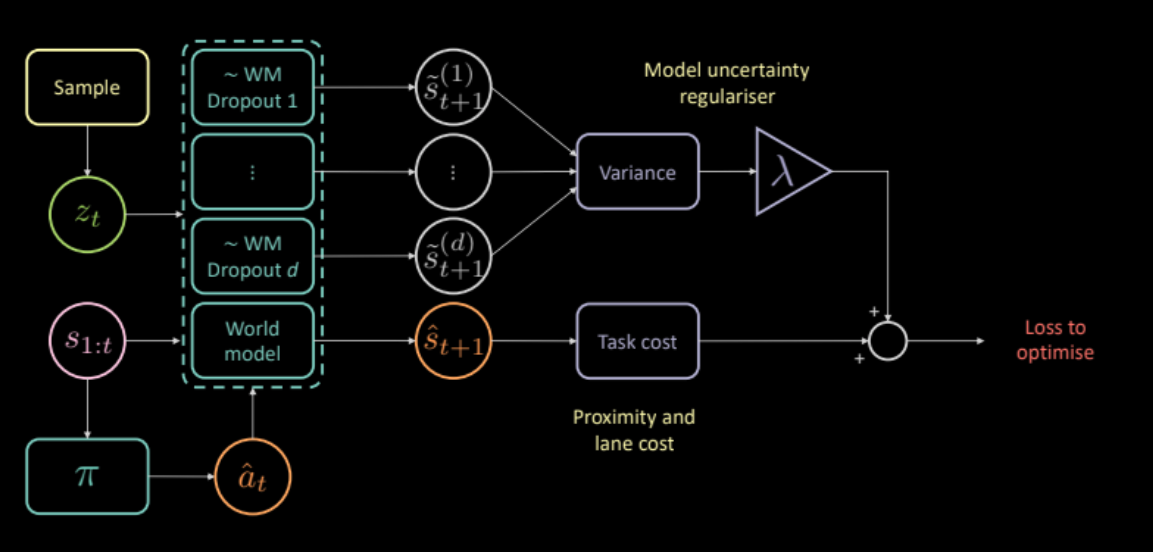
Figure 24 : Architecture de modèle basée sur la régularisation de l'incertitude

Alors, la régularisation de l’incertitude nous aide-t-elle à apprendre une meilleure politique ? Oui. La politique ainsi apprise est meilleure que les modèles précédents.

Figure 25 : Politique apprise basée sur la régularisation de l'incertitude

Évaluation

La figure 26 montre à quel point notre agent a appris à conduire dans un trafic dense. La voiture jaune est le conducteur d’origine, la voiture bleue est notre agent entraîné et toutes autres, les voitures vertes, sont celles qui ne peuvent pas être contrôlées.

Figure 26 : Performance du modèle avec régularisation de l'incertitude