Apprentissage profond pour une prédiction utilisant la structure

Prédiction utilisant la structure

Nous sommes dans le cas de la prédiction de la variable $y$ pour une entrée $x$ donnée qui est mutuellement dépendante et contrainte plutôt que des valeurs scalaires discrètes ou réelles. Alors la variable de sortie n’appartient pas à une seule catégorie mais peut avoir des valeurs possibles exponentielles ou infinies. Par exemple, dans le cas de la reconnaissance de la parole/écriture ou de traduction en langage naturel, la sortie doit être grammaticalement correcte et il n’est pas possible de limiter le nombre de possibilités de sortie. La tâche du modèle est de capturer la structure séquentielle, spatiale ou combinatoire dans le domaine du problème.

Premiers travaux sur la prédiction utilisant la structure

Ce vecteur est transmis à un réseau de neurones à retard temporel (TDNN pour Time Delay Neural Network) qui donne un vecteur de caractéristiques qui, dans le cas de systèmes de modèles, peut être comparé au softmax représentant une catégorie. Un problème qui se pose dans le cas de la reconnaissance de la parole est que différentes personnes peuvent prononcer le même mot de différentes manières et à des vitesses différentes. Pour résoudre ce problème, on utilise la déformation temporelle dynamique (DTW pour Dynamic Time Warping).

L’idée est de fournir au système un ensemble de patrons pré-enregistrés qui correspondent à des vecteurs de séquences ou de caractéristiques qui ont été enregistrés par quelqu’un. Le réseau neuronal est entraîné en même temps que le patron afin que le système apprenne à reconnaître le mot pour différentes prononciations. La variable latente nous permet de modifier le vecteur de caractéristique de manière à ce qu’il corresponde à la longueur des modèles.

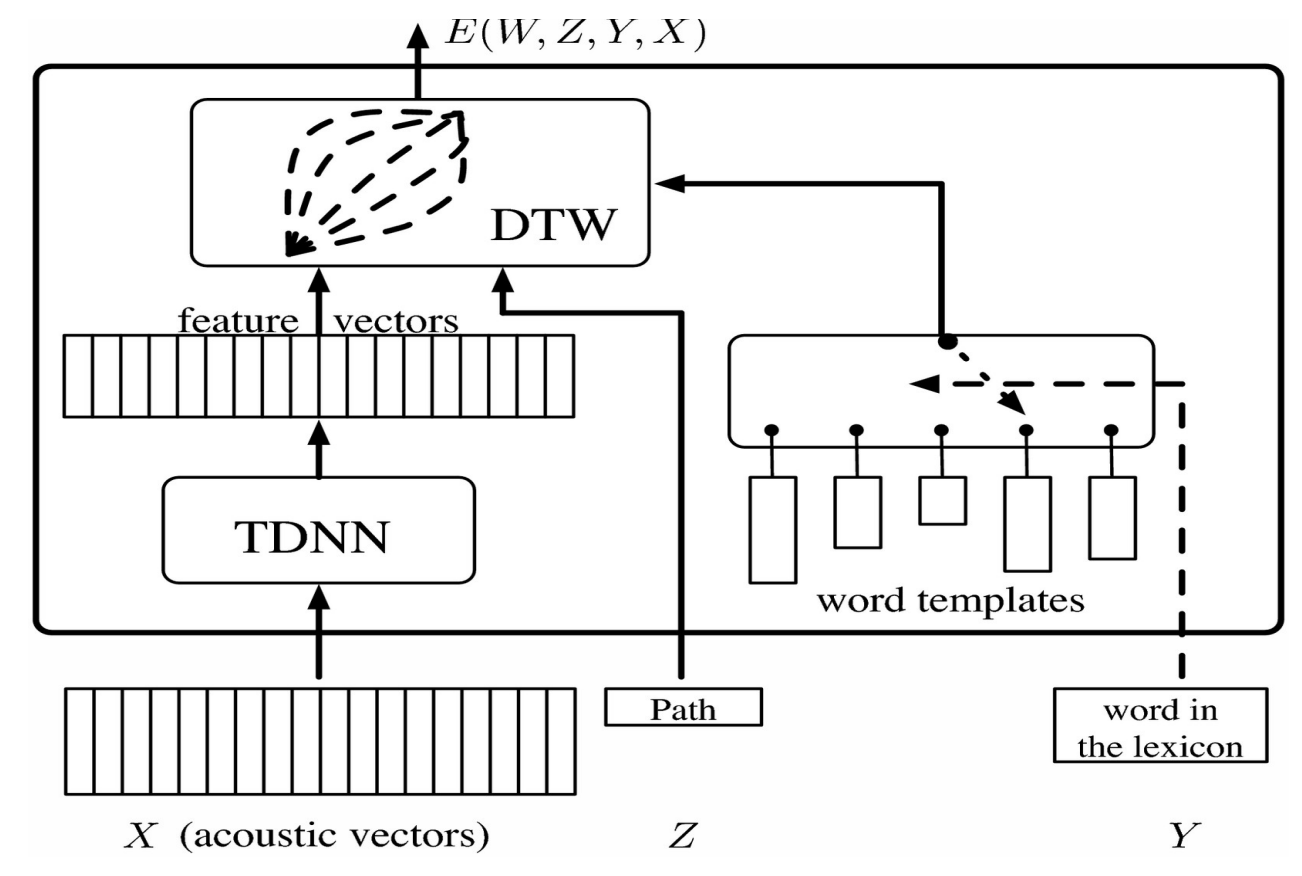
Figure 1 : Schéma du modèle

Cela peut être visualisé sous forme de matrice en organisant les vecteurs de caractéristiques du TDNN horizontalement et les modèles de mots verticalement. Chaque entrée dans la matrice correspond à la distance entre les vecteurs de caractéristiques. Cela peut être visualisé comme un problème de graphe où le but est de partir du coin inférieur gauche et d’atteindre le coin supérieur droit en parcourant le chemin qui minimise la distance.

Pour entraîner ce modèle à variable latente, nous devons rendre l’énergie pour les bonnes réponses aussi petite que possible et plus grande pour chaque mauvaise réponse. Pour ce faire, nous utilisons une fonction objectif qui prend des patrons pour les mots incorrects, les repousse loin de la séquence actuelle des caractéristiques et rétropropage les gradients.

Graphes factoriels à base d’énergie

L’idée derrière les graphes factoriels à base d’énergie est de construire un EBM dans lequel l’énergie est la somme de termes énergétiques partiels ou lorsque la probabilité est un produit de facteurs. L’avantage de ces modèles est que des algorithmes d’inférence efficaces peuvent être utilisés.

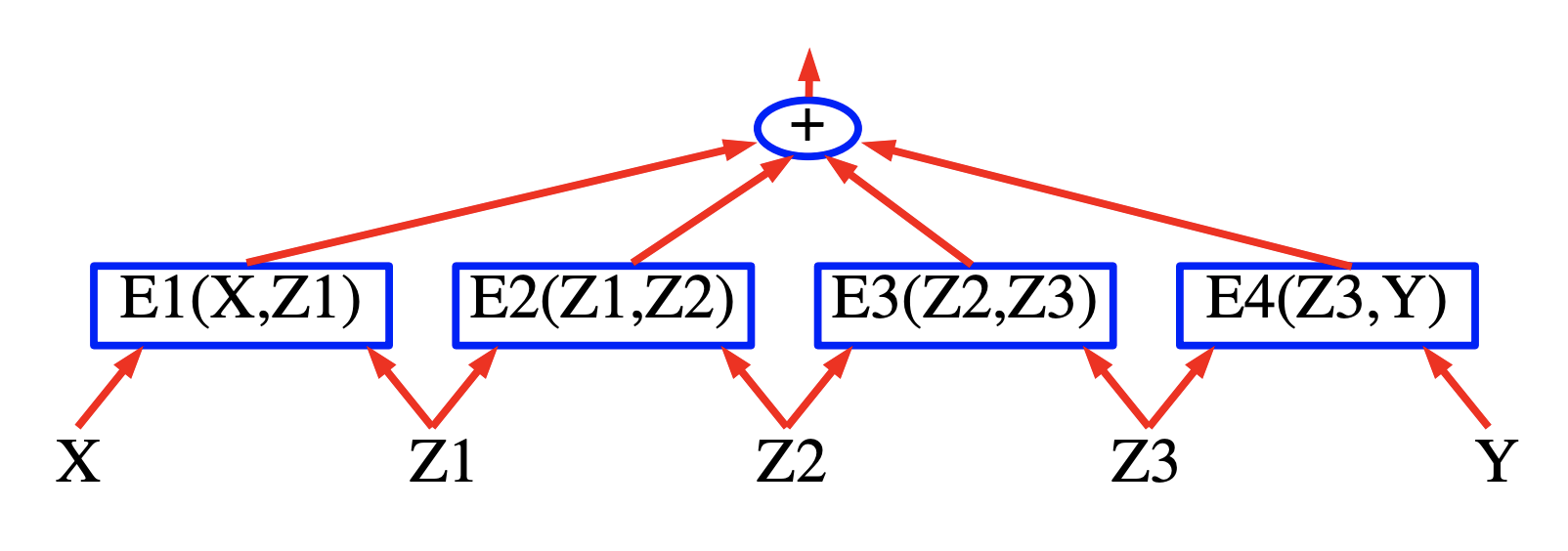
Figure 2 : Graphes factoriels à base d'énergie

Etiquetage des séquences

Le modèle prend un signal vocal d’entrée $X$ et sort les labels $Y$ de telle sorte qu’ils minimisent le terme d’énergie total.

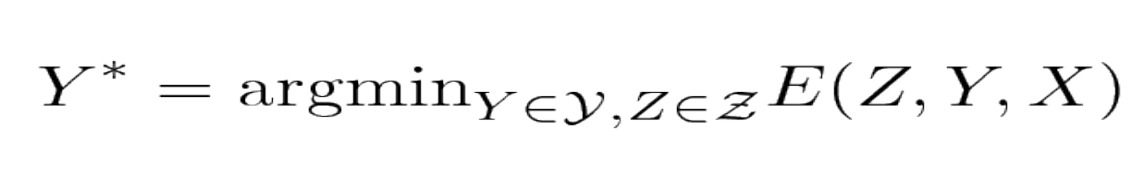
Figure 3 : Minimisation de l'énergie

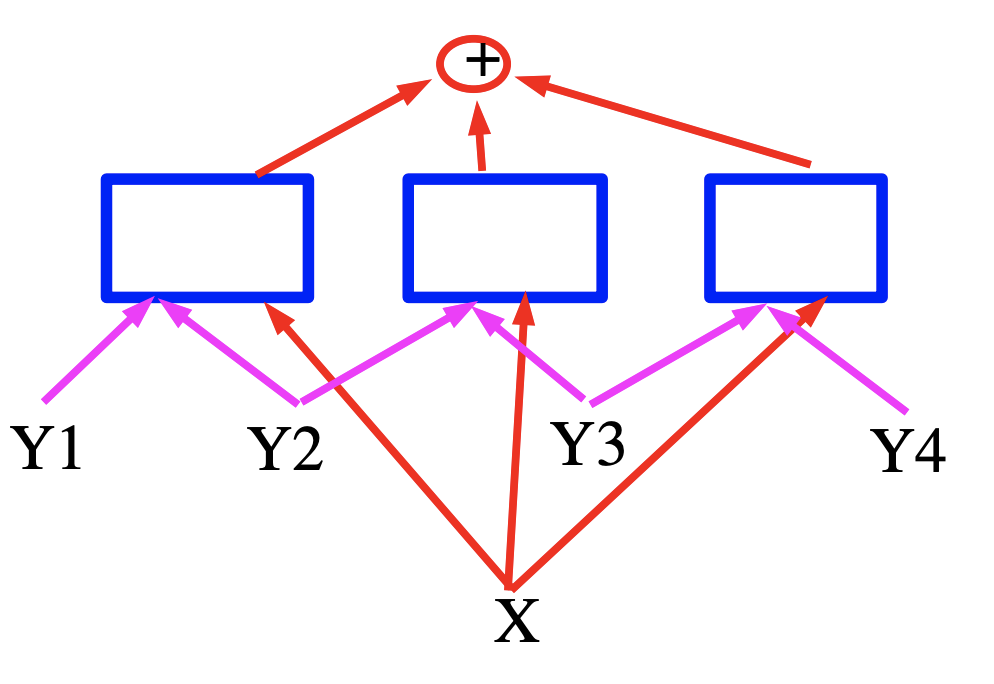
Figure 4 : Minimisation de l'énergie sous la forme d'un graphe

Dans ce cas, l’énergie est une somme de trois termes représentés par des carrés bleus qui sont des réseaux de neurones qui produisent des vecteurs de caractéristiques pour les variables d’entrée. Dans le cas de la reconnaissance vocale, $X$ peut être considéré comme un signal vocal, les carrés implémentent les contraintes grammaticales et $Y$ représente les labels de sortie générées.

Inférence efficiente pour les graphes factoriels à base d’énergie

Un tutoriel sur l’apprentissage à base d’énergie est disponible ici (Le Cun et al. (2006)).

L’apprentissage et l’inférence avec les modèles à base d’énergie impliquent une minimisation de l’énergie sur l’ensemble des réponses $\mathcal{Y}$ et des variables latentes $\mathcal{Z}$. Lorsque la cardinalité de $\mathcal{Y}\times \mathcal{Z}$ est importante, cette minimisation peut devenir insoluble. Une approche du problème consiste à exploiter la structure de la fonction énergie afin d’effectuer la minimisation de manière efficace. Un cas où la structure peut être exploitée se produit lorsque l’énergie peut être exprimée comme une somme de fonctions individuelles (appelées facteurs) qui dépendent chacune de différents sous-ensembles des variables de $\mathcal{Y}$ et $\mathcal{Z}$. Ces dépendances sont mieux exprimées sous la forme d’un graphe factoriel. Les graphes factoriels sont une forme générale de modèles graphiques ou de réseaux de croyances.

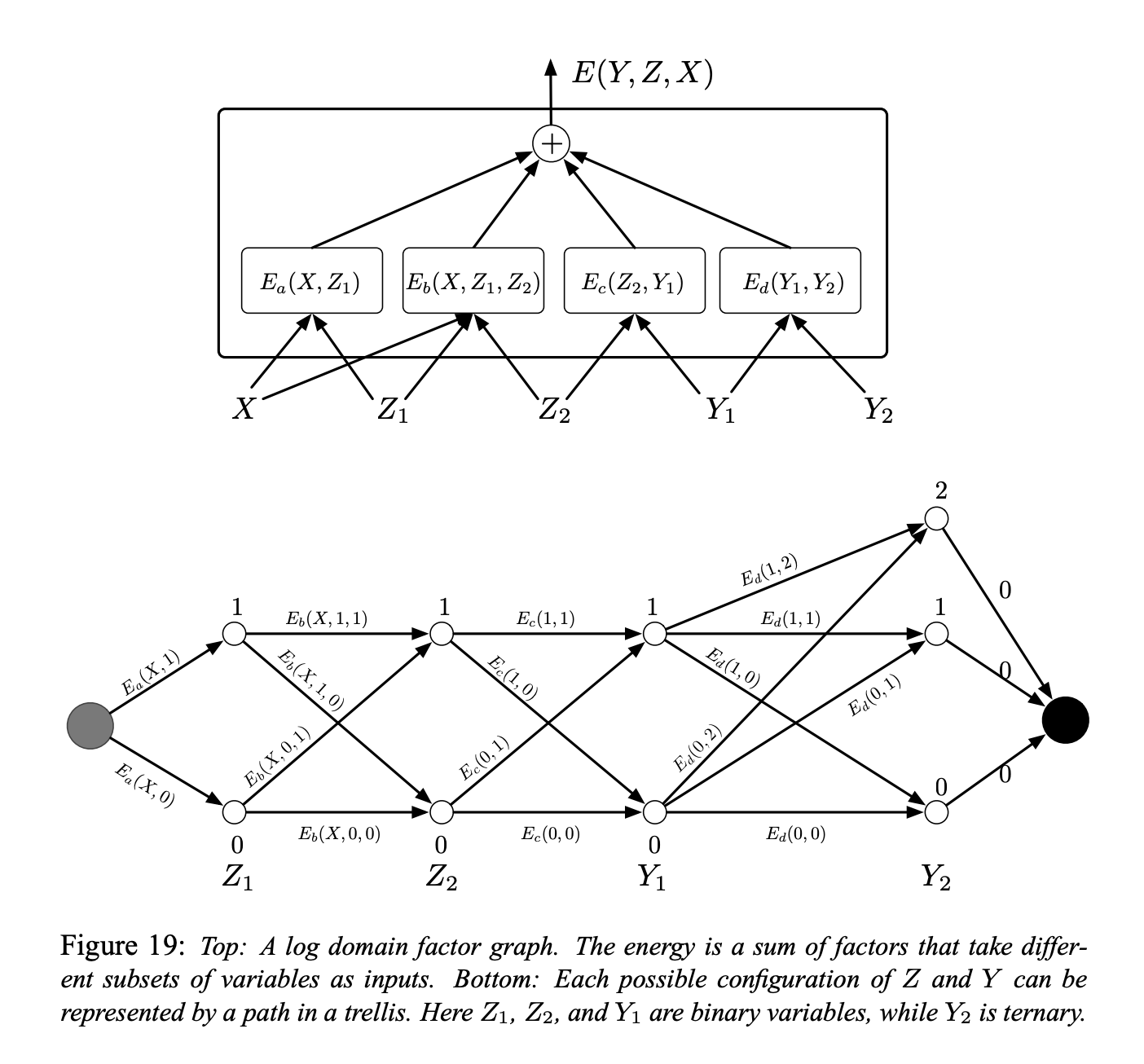
Figure 5 : Graphes factoriels à base d'énergie

Un exemple simple de graphe de facteur est présenté à la figure 5 (en haut). La fonction énergie est la somme de quatre facteurs :

où $Y = [Y_1, Y_2]$ sont les variables de sortie et $Z = [Z_1, Z_2]$ sont les variables latentes. Chaque facteur peut être considéré comme représentant des contraintes souples entre les valeurs de ses variables d’entrée. Le problème d’inférence consiste à trouver :

Supposons que $Z_1$, $Z_2$ et $Y_1$ sont des variables binaires discrètes et que $Y_2$ est une variable ternaire. La cardinalité du domaine de $X$ est sans importance puisque $X$ est toujours observé. Le nombre de configurations possibles de $Z$ et $Y$ étant donné $X$ est de $2 \times 2 \times 2 \times 3 = 24$. Un algorithme de minimisation naïf par recherche exhaustive évaluerait la fonction énergie entière $24$ fois ($96$ évaluations à facteur unique).

Cependant, nous remarquons que pour un $X$ donné, $E_a$ n’a que deux configurations d’entrée possibles : $Z_1 = 0$ et $Z_1 = 1$. De même, $E_b$ et $E_c$ n’ont que 4 configurations d’entrée possibles, et $E_d$ en a $6$, il n’est pas nécessaire d’avoir plus de $2 + 4 + 4 + 6 = 16$ d’évaluations de facteur unique.

Nous pouvons donc précalculer les $16$ valeurs de facteurs et les placer sur les arcs d’un trellis comme le montre la figure 5 (en bas).

Les nœuds de chaque colonne représentent les valeurs possibles d’une seule variable. Chaque arc est pondéré par l’énergie de sortie du facteur pour les valeurs correspondantes de ses variables d’entrée. Avec cette représentation, un seul chemin du nœud de départ au nœud d’arrivée représente une configuration possible de toutes les variables. La somme des poids le long d’un chemin est égale à l’énergie totale pour la configuration correspondante. Par conséquent, le problème d’inférence peut être réduit à la recherche du plus court chemin dans ce graphe. Ceci peut être réalisé en utilisant une méthode de programmation dynamique telle que l’algorithme de Viterbi ou l’algorithme A*. Le coût est proportionnel au nombre d’arêtes ($16$) qui est exponentiellement plus petit que le nombre de chemins en général.

Pour calculer $E(Y, X) = \min_{z\in Z} E(Y, z, X)$ nous suivons la même procédure mais nous limitons le graphe au sous-ensemble des arcs qui sont compatibles avec la valeur prescrite de $Y$.

La procédure ci-dessus est parfois appelée l’algorithme min-sum et il s’agit de la version logarithmique du domaine du max-product traditionnel pour les modèles graphiques. La procédure peut facilement être généralisée aux graphes factoriels où les facteurs prennent plus de deux variables comme entrées et aux graphes factoriels qui ont une structure arborescente au lieu d’une structure de chaîne.

Toutefois, elle ne s’applique qu’aux graphes de facteurs qui sont des arbres bipartites (sans boucles). Lorsque des boucles sont présentes dans le graphe, l’algorithme min-sum peut donner une solution approximative lorsqu’il est répété, ou peut ne pas converger du tout. Dans ce cas, un algorithme de descente tel que l’annealing simulé peut être utilisé.

Graphes factoriels simples à base d’énergie avec facteurs peu profonds

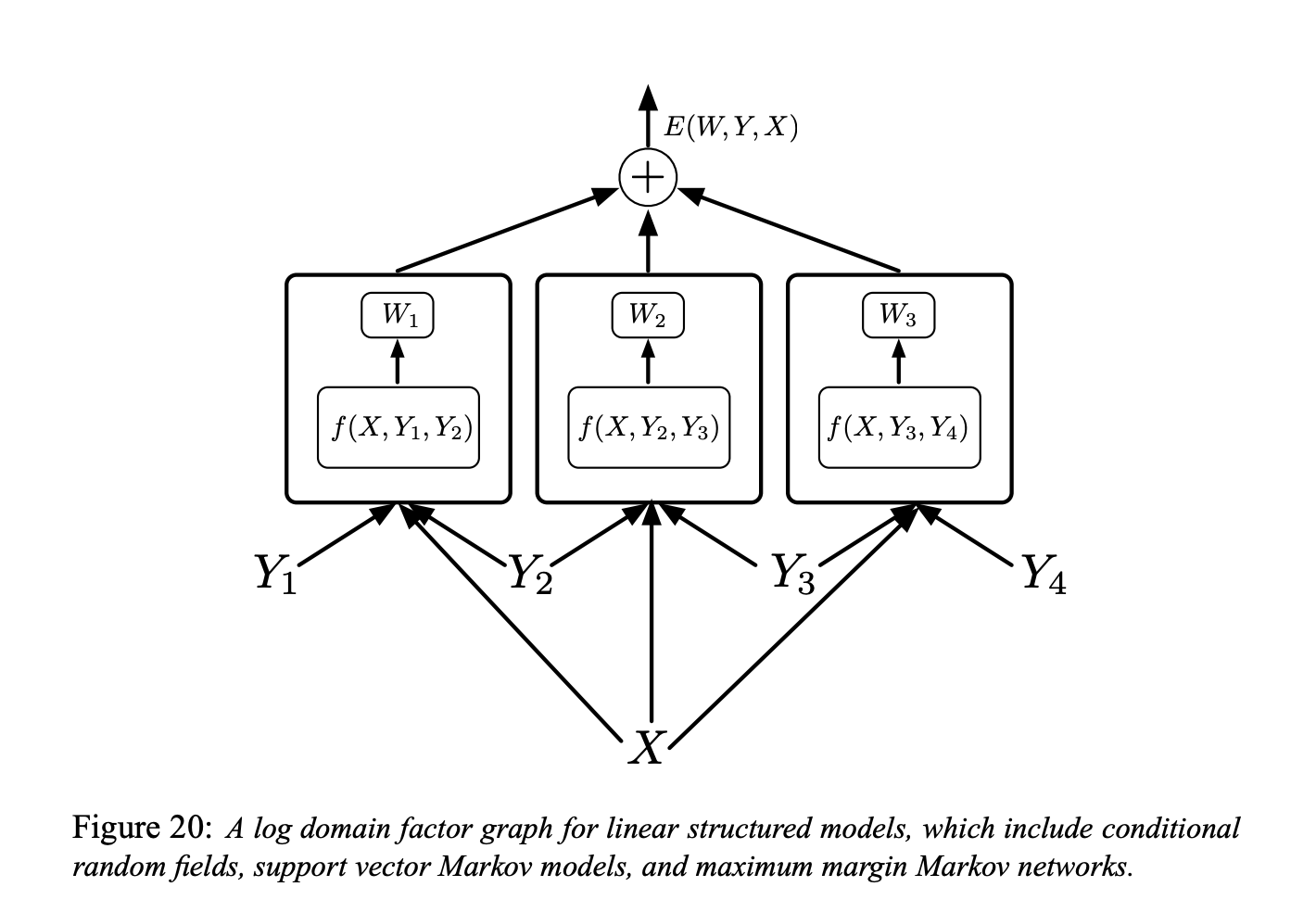
Figure 6 : Graphe factoriel pour des modèles à structure linéaire

Chaque facteur dans la figure 6 est une fonction de paramètres entraînables dépendant de $X$ et d’une paire de labels individuels $(Y_m, Y_n)$. En général, chaque facteur peut dépendre de plus de deux labels individuels mais nous limitons la discussion aux facteurs par paires pour simplifier la notation :

Ici, $\mathcal{F}$ désigne l’ensemble des facteurs (l’ensemble des paires de labels individuels qui ont une interdépendance directe), $W_{m n}$ est le vecteur de paramètre pour le facteur $(m, n),$ et $f_{m n}\left(X, Y_{m}, Y_{n}\right)$ est un vecteur de caractéristique (fixe). Le vecteur paramètre global $W$ est la concaténation de tous les $W_{m n}.$

On peut alors réfléchir au type de la fonction de perte. Voici plusieurs modèles différents.

Champ aléatoire conditionnel

Nous pouvons utiliser la fonction de perte de log-vraisemblance négative pour entraîner un modèle à structure linéaire.

Il s’agit du champ aléatoire conditionnel.

L’intuition est que nous voulons que l’énergie de la bonne réponse soit basse et que le logarithme de l’exponentielle pour toutes les réponses, y compris la bonne, soit grand.

Voici la définition formelle de la fonction de perte de probabilité logarithmique négative :

Réseaux de Markov à marge maximale et les SVMs latentes

Nous pouvons également utiliser la fonction de perte Hinge pour l’optimisation.

L’intuition est que nous voulons que l’énergie de la bonne réponse soit faible. Puis parmi toutes les configurations possibles de réponses incorrectes, nous allons chercher celle qui a l’énergie la plus faible parmi toutes les mauvaises réponses. Nous allons ensuite augmenter l’énergie de celle-ci. Nous n’avons pas besoin d’augmenter l’énergie pour les autres mauvaises réponses parce qu’elles sont de toute façon plus grandes.

C’est l’idée qui sous-tend les réseaux de Markov à marge maximale et les SVMs latentes.

Modèle avec une strcuture perceptron

Nous pouvons entraîner un modèle linéaire en utilisant la perte de perceptron.

Collins (2000 et 2002) a préconisé son utilisation pour les modèles linéaires structurés dans le contexte du traitement du langage naturel :

où $Y^{* i}=\operatorname{argmin}_{y \in \mathcal{Y}} E\left(W, y, X^{i}\right)$ est la réponse produite par le système.

Premières pistes sur un entraînement discriminant pour la reconnaissance de la parole et de l’écriture

Minimum Empirical Error Loss (Ljolje et Rabiner 1990) : En entraînant au niveau de la séquence, les auteurs n’indiquent pas au système tel ou tel son ou endroit. Ils donnent au système la phrase d’entrée et sa transcription en termes de mots, et demandent au système de la comprendre en faisant une distorsion temporelle. Ils n’ont pas utilisé de réseaux de neurones et disposent d’autres moyens pour transformer les signaux vocaux en catégories de sons.

Graph Transformer Network (GTN)

Ici, le problème est que nous avons une séquence de chiffres en entrée et que nous ne savons pas comment faire la segmentation. Nous pouvons néanmoins construire un graphe dans lequel chaque chemin est un moyen de décomposer la séquence de caractères. Nous allons alors trouver le chemin avec la plus faible énergie. En gros cela revient à trouver le chemin le plus court. Voici un exemple concret de la façon dont cela fonctionne.

Nous avons en entrée l’image du nombre 34. On la passe dans le segmenteur et on obtient plusieurs segmentations alternatives. Ces segmentations sont des moyens de regrouper ces blocs de choses. Chaque chemin dans le graphe de segmentation correspond à une façon particulière de regrouper les taches d’encre.

Figure 7 : Image d'un 34

Nous passons chaque segment par le même ConvNet de reconnaissance de caractères et obtenons une liste de $10$ scores ($2$ ici mais généralement on en a $10$ représentant les $10$ catégories/chiffres). Par exemple, 1 [0,1] signifie que l’énergie est de $0,1$ pour la catégorie $1$. On obtient alors un graphe pouvant être considéré comme une forme étrange de tenseur peu dense). C’est un tenseur qui pour chaque configuration possible de cette variable, demande le coût de la variable. Il s’agit davantage d’une distribution sur les tenseurs, ou une distribution logarithmique car nous parlons d’énergies.

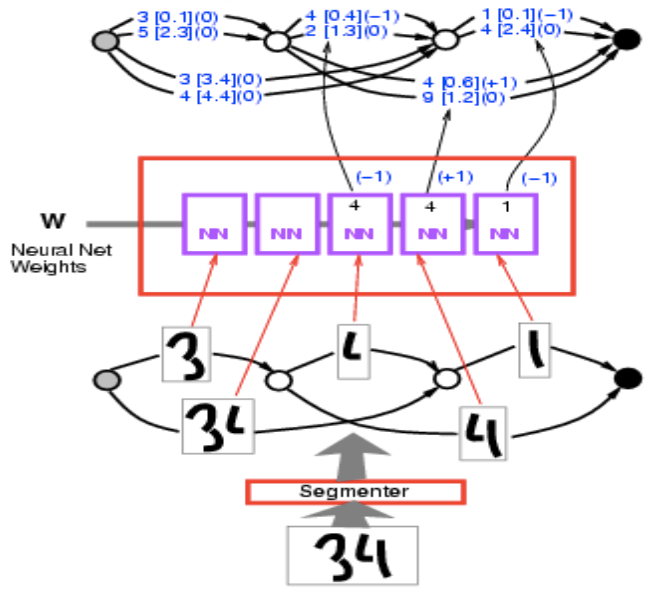
Figure 8 : Graphe d'ensemble

Si on prend le graphe de la figure 9 et devons calculer l’énergie de la bonne réponse ($34$), nous devons sélectionner dans ces chemins ceux donnant la bonne réponse. Il y en a deux, l’une est l’énergie $3,4 + 2,4 = 5,8$ et l’autre $0,1 + 0,6 = 0,7$. Il nous reste alors plus qu’à prendre le chemin qui a l’énergie la plus faible. Ici, nous obtenons le chemin avec l’énergie $0,7$.

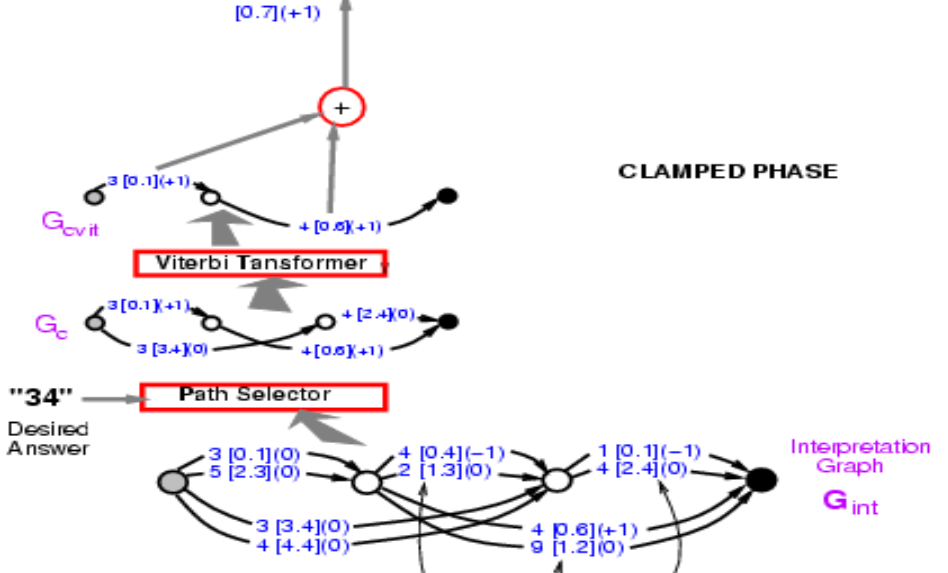
Figure 9 : Graphe avec les valeurs d'énergie

Trouver le chemin est donc comme minimiser sur une variable latente où la variable latente est le chemin choisi. Conceptuellement, il s’agit d’un modèle d’énergie avec une variable latente comme chemin.

Nous avons donc l’énergie du chemin correct, $0,7$. Ce que nous devons faire maintenant, c’est rétropropager le gradient à travers toute cette structure, afin de pouvoir modifier le poids dans le ConvNet de telle sorte que l’énergie finale diminue. Cela semble intimidant, mais c’est tout à fait possible. Comme tout ce système est construit à partir d’éléments que nous connaissons déjà, le réseau neuronal est classique. Le sélecteur de chemin et le transformer de Viterbi sont essentiellement des interrupteurs qui choisissent une arête particulière ou non.

Alors comment rétropropager ? Le point $0,7$ est la somme de $0,1$ et $0,6$. Donc, les points $0,1$ et $0,6$ auront tous deux un gradient de $+1$, indiqué entre parenthèses dans la figure 9. Ensuite, le transformer de Viterbi n’a qu’à sélectionner un chemin parmi deux. Il suffit donc de copier le gradient pour l’arête correspondante dans le graphe d’entrée et de définir le gradient des autres trajectoires comme étant nulles car non retenues. C’est exactement ce qui se passe dans le max-pooling ou le mean-pooling. Le sélecteur de trajectoire est le même, c’est juste un système qui sélectionne la bonne réponse. A noter qu’à ce stade, le 3 [0.1] (0) dans le graphe de la figure 9, deviendrait 3 [0.1] (1). Nous pouvons alors rétroprogager le gradient à travers le réseau rendant l’énergie de la bonne réponse faible.

Ce qui est important ici, c’est que cette structure est dynamique. Car si on nous donne une nouvelle entrée, le nombre d’instances du réseau névralgique changera avec le nombre de segmentations et les graphes dérivés changeront également. Nous devons faire une rétropropagation à travers cette structure dynamique. C’est là que des frameworks comme PyTorch sont vraiment importantes.

Cette phase de rétropropagation rend l’énergie de la bonne réponse faible. Et il y aura une deuxième phase où nous allons rendre l’énergie de la mauvaise réponse grande. Dans ce cas, nous laissons le système choisir la réponse qu’il veut. Il s’agira d’une forme simplifiée d’entraînement discriminatoire pour la prédiction des structures qui utilisent la perte de perception.

Les premières étapes de la deuxième phase sont exactement les mêmes que celles de la première. Le transformer de Viterbi ici choisi simplement le meilleur chemin avec la plus faible énergie. Nous ne nous soucions pas de savoir si ce chemin est correct ou non. L’énergie obtenue ici sera plus petite ou égale à celle obtenue dans la première phase puisque l’énergie obtenue ici est la plus petite de toutes les voies possibles.

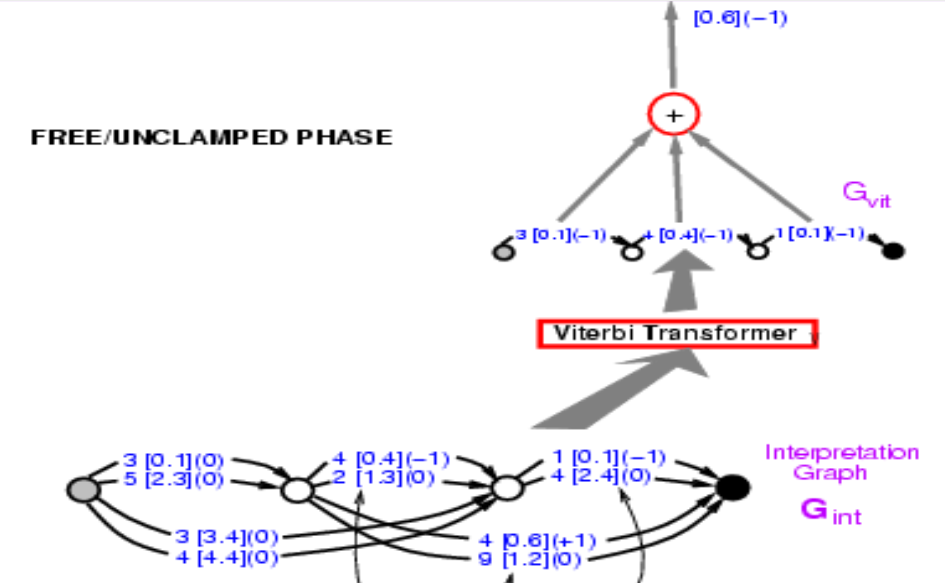
Figure 10 : Raisonnement de la rétropropagation

En mettant la phase une et deux ensemble, la fonction de perte devrait être $énergie1 - énergie2$. Avant, nous avons introduit la rétropropagation par la partie gauche et maintenant nous devons en fait rétropropager à travers toute la structure. Quel que soit le chemin sur le côté gauche on obtiendra $+1$ et quel que soit le chemin sur le côté droit on obtiendra $-1$. Donc 3 [0,1] est apparu dans les deux chemins et nous obtenons un gradient nul. Si nous faisons cela, le système fini par minimiser la différence entre l’énergie de la bonne réponse et l’énergie de la meilleure réponse quelle qu’elle soit. La fonction de perte ici est la perte de perceptron.

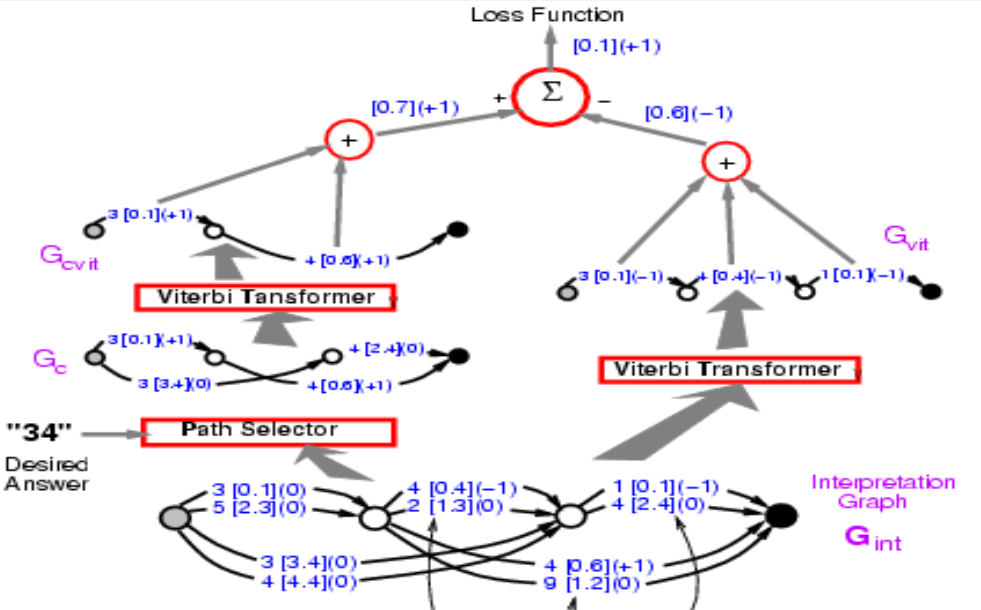
Figure 11 : Raisonnement de la rétropropagation sur deux chemins

Questions des étudiants

Pourquoi l’inférence est-elle facile dans le cas des graphes factoriels à base d’énergie ?

L’inférence dans le cas d’un EBM avec variable latente implique l’utilisation de techniques exhaustives telles que la descente de gradient pour minimiser l’énergie. Cependant dans ce cas puisque l’énergie est la somme des facteurs, des techniques telles que la programmation dynamique peuvent être utilisées à la place.

Que faire si les variables latentes des graphes factoriels sont des variables continues ? Peut-on encore utiliser l’algorithme min-sum ?

Nous ne le pouvons pas car nous ne pouvons pas rechercher toutes les combinaisons possibles pour toutes les valeurs des facteurs. Cependant, dans ce cas, les énergies nous donnent aussi un avantage car nous pouvons faire des optimisations indépendantes. Comme la combinaison de $Z_1$ et $Z_2$ n’affecte que $E_b$ dans la figure 5. Nous pouvons faire des optimisations indépendantes et une programmation dynamique pour faire l’inférence.

Les boîtes font-elles référence à des ConvNets séparés ?

Elles sont partagées. Ce sont des copies multiples du même ConvNet. Il s’agit simplement d’un réseau de reconnaissance de caractères.