Algebre linéaire et convolutions

🎙️ Alfredo Canziani

Rappel d’algèbre linéaire

Cette partie est une récapitulation de l’algèbre linéaire de base dans le contexte des réseaux de neurones. Nous commençons par une simple couche cachée $\boldsymbol{h}$ :

\[\boldsymbol{h} = f(\boldsymbol{z})\]

La sortie est une fonction non linéaire $f$ appliquée à un vecteur $z$. Ici, $z$ est la sortie d’une transformation affine $\boldsymbol{A} \in\mathbb{R^{m\times n}}$ au vecteur d’entrée $\boldsymbol{x} \in\mathbb{R^n}$ :

\[\boldsymbol{z} = \boldsymbol{A} \boldsymbol{x}\]

Par souci de simplicité, les biais sont ignorés. L’équation linéaire peut être développée comme suit :

\[\boldsymbol{A}\boldsymbol{x} = \begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n}\\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{pmatrix} \begin{pmatrix} x_1 \\ \vdots \\x_n \end{pmatrix} = \begin{pmatrix} \text{---} \; \boldsymbol{a}^{(1)} \; \text{---} \\ \text{---} \; \boldsymbol{a}^{(2)} \; \text{---} \\ \vdots \\ \text{---} \; \boldsymbol{a}^{(m)} \; \text{---} \\ \end{pmatrix} \begin{matrix} \rvert \\ \boldsymbol{x} \\ \rvert \end{matrix} = \begin{pmatrix} {\boldsymbol{a}}^{(1)} \boldsymbol{x} \\ {\boldsymbol{a}}^{(2)} \boldsymbol{x} \\ \vdots \\ {\boldsymbol{a}}^{(m)} \boldsymbol{x} \end{pmatrix}_{m \times 1}\]

où $\boldsymbol{a}^{(i)}$ est la $i$-ième ligne de la matrice $\boldsymbol{A}$.

Pour comprendre la signification de cette transformation, analysons une composante de $\boldsymbol{z}$ telle que $a^{(1)}\boldsymbol{x}$. Soit $n=2$, alors $\boldsymbol{a} = (a_1,a_2)$ et $\boldsymbol{x} = (x_1,x_2)$.

$\boldsymbol{a}$ et $\boldsymbol{x}$ peuvent être dessinés comme des vecteurs dans l’axe des coordonnées 2D. Maintenant, si l’angle entre $\boldsymbol{a}$ et $\hat{\boldsymbol{\imath}}$ est $\alpha$ et l’angle entre $\boldsymbol{x}$ et $\hat{\boldsymbol{\imath}}$ est $\xi$, alors avec les formules trigonométriques $a^\top\boldsymbol{x}$ (la traduction impose d’utiliser la notation anglo-saxonne de la transposée) peut être étendu comme :

\[\begin {aligned} \boldsymbol{a}^\top\boldsymbol{x} &= a_1x_1+a_2x_2\\ &=\lVert \boldsymbol{a} \rVert \cos(\alpha)\lVert \boldsymbol{x} \rVert \cos(\xi) + \lVert \boldsymbol{a} \rVert \sin(\alpha)\lVert \boldsymbol{x} \rVert \sin(\xi)\\ &=\lVert \boldsymbol{a} \rVert \lVert \boldsymbol{x} \rVert \big(\cos(\alpha)\cos(\xi)+\sin(\alpha)\sin(\xi)\big)\\ &=\lVert \boldsymbol{a} \rVert \lVert \boldsymbol{x} \rVert \cos(\xi-\alpha) \end {aligned}\]

La sortie mesure l’alignement de l’entrée sur une ligne spécifique de la matrice $\boldsymbol{A}$. Cela peut être compris en observant l’angle entre les deux vecteurs, $\xi-\alpha$. Lorsque $\xi = \alpha$, les deux vecteurs sont parfaitement alignés et le maximum est atteint. Si $\xi - \alpha = \pi$, alors $\boldsymbol{a}^\top\boldsymbol{x}$ atteint son minimum et les deux vecteurs sont orientés dans des directions opposées. En substance, la transformation linéaire permet de voir la projection d’une entrée vers différentes orientations définies par $A$. Cette intuition est également extensible à des dimensions plus élevées.

Une autre façon de comprendre la transformation linéaire est de comprendre que $\boldsymbol{z}$ peut aussi être étendu comme :

\[\boldsymbol{A}\boldsymbol{x} = \begin{pmatrix} \vert & \vert & & \vert \\ \boldsymbol{a}_1 & \boldsymbol{a}_2 & \cdots & \boldsymbol{a}_n \\ \vert & \vert & & \vert \\ \end{pmatrix} \begin{matrix} \rvert \\ \boldsymbol{x} \\ \rvert \end{matrix} = x_1 \begin{matrix} \rvert \\ \boldsymbol{a}_1 \\ \rvert \end{matrix} + x_2 \begin{matrix} \rvert \\ \boldsymbol{a}_2 \\ \rvert \end{matrix} + \cdots + x_n \begin{matrix} \rvert \\ \boldsymbol{a}_n \\ \rvert \end{matrix}\]

La sortie est la somme pondérée des colonnes de la matrice $\boldsymbol{A}$. Par conséquent, le signal n’est rien d’autre qu’une composition de l’entrée.

Extension de l’algèbre linéaire aux convolutions

Nous étendons maintenant l’algèbre linéaire aux convolutions en utilisant l’exemple de l’analyse des données audio. Nous commençons par représenter une couche entièrement connectée comme une forme de multiplication matricielle :

\[\begin{bmatrix} w_{11} & w_{12} & w_{13}\\ w_{21} & w_{22} & w_{23}\\ w_{31} & w_{32} & w_{33}\\ w_{41} & w_{42} & w_{43} \end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ x_3 \end{bmatrix} = \begin{bmatrix} y_1\\ y_2\\ y_3\\ y_4 \end{bmatrix}\]

Dans cet exemple, la matrice de poids a une taille de $4 \times 3$, le vecteur d’entrée a une taille de $3 \times 1$ et le vecteur de sortie a une taille de $4 \times 1$.

Cependant, pour les données audio, les données sont beaucoup plus longues (pas de $3$ échantillons). Le nombre d’échantillons dans les données audio est égal à la durée de l’audio (par exemple 3 secondes) multipliée par le taux d’échantillonnage (par exemple $22,05$ kHz). Comme indiqué ci-dessous, le vecteur d’entrée $\boldsymbol{x}$ est assez long. En conséquence, la matrice de poids devient « grosse ».

\[\begin{bmatrix} w_{11} & w_{12} & w_{13} & w_{14} & \cdots &w_{1k}& \cdots &w_{1n}\\ w_{21} & w_{22} & w_{23}& w_{24} & \cdots & w_{2k}&\cdots &w_{2n}\\ w_{31} & w_{32} & w_{33}& w_{34} & \cdots & w_{3k}&\cdots &w_{3n}\\ w_{41} & w_{42} & w_{43}& w_{44} & \cdots & w_{4k}&\cdots &w_{4n} \end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ x_3\\ x_4\\ \vdots\\ x_k\\ \vdots\\ x_n \end{bmatrix} = \begin{bmatrix} y_1\\ y_2\\ y_3\\ y_4 \end{bmatrix}\]

La formulation ci-dessus sera difficile à entraîner. Heureusement, il existe des moyens de la simplifier.

Propriété : localité

En raison de la localité (c’est-à-dire que nous ne nous soucions pas des points de données qui sont éloignés) des données, $w_{1k}$ de la matrice de pondération ci-dessus, peut être rempli par des $0$ lorsque $k$ est relativement important. Par conséquent, la première ligne de la matrice devient un noyau de taille $3$. Désignons ce noyau de taille $3$ comme $\boldsymbol{a}^{(1)} = \begin{bmatrix} a_1^{(1)} & a_2^{(1)} & a_3^{(1)} \end{bmatrix}$.

\[\begin{bmatrix} a_1^{(1)} & a_2^{(1)} & a_3^{(1)} & 0 & \cdots &0& \cdots &0\\ w_{21} & w_{22} & w_{23}& w_{24} & \cdots & w_{2k}&\cdots &w_{2n}\\ w_{31} & w_{32} & w_{33}& w_{34} & \cdots & w_{3k}&\cdots &w_{3n}\\ w_{41} & w_{42} & w_{43}& w_{44} & \cdots & w_{4k}&\cdots &w_{4n} \end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ x_3\\ x_4\\ \vdots\\ x_k\\ \vdots\\ x_n \end{bmatrix} = \begin{bmatrix} y_1\\ y_2\\ y_3\\ y_4 \end{bmatrix}\]

Propriété : stationnarité

Les signaux de données naturelles ont la propriété d’être stationnaires (c’est-à-dire que certains modèles/motifs se répètent). Cela nous permet de réutiliser le noyau $\mathbf{a}^{(1)}$ que nous avons défini précédemment. Nous utilisons ce noyau en le plaçant chaque fois un pas plus loin (c’est-à-dire que le pas est de $1$), ce qui donne le résultat suivant :

\[\begin{bmatrix} a_1^{(1)} & a_2^{(1)} & a_3^{(1)} & 0 & 0 & 0 & 0&\cdots &0\\ 0 & a_1^{(1)} & a_2^{(1)} & a_3^{(1)} & 0&0&0&\cdots &0\\ 0 & 0 & a_1^{(1)} & a_2^{(1)} & a_3^{(1)} & 0&0&\cdots &0\\ 0 & 0 & 0& a_1^{(1)} & a_2^{(1)} &a_3^{(1)} &0&\cdots &0\\ 0 & 0 & 0& 0 & a_1^{(1)} &a_2^{(1)} &a_3^{(1)} &\cdots &0\\ \vdots&&\vdots&&\vdots&&\vdots&&\vdots \end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ x_3\\ x_4\\ \vdots\\ x_k\\ \vdots\\ x_n \end{bmatrix}\]

La partie supérieure droite et la partie inférieure gauche de la matrice sont toutes deux remplies de $0$ grâce à la localité, ce qui entraîne une certaine éparsité. La réutilisation d’un certain noyau encore et encore est appelée partage du poids.

Plusieurs couches de la matrice de Toeplitz

Après ces changements, le nombre de paramètres qui nous reste est de $3$ (c’est-à-dire $a_1,a_2,a_3$). Par rapport à la matrice de pondération précédente, qui comportait $12$ paramètres (c’est-à-dire $w_{11},w_{12},\cdots,w_{43}$), le nombre actuel de paramètres est trop restrictif et nous souhaitons le développer.

La matrice précédente peut être considérée comme une couche (c’est-à-dire une couche convolutive) avec le noyau $\boldsymbol{a}^{(1)}$. Nous pouvons alors construire plusieurs couches avec différents noyaux $\boldsymbol{a}^{(2)}$, $\boldsymbol{a}^{(3)}$, etc.

Chaque couche a une matrice contenant un seul noyau qui est répliqué plusieurs fois. Ce type de matrice est appelé matrice de Toeplitz. Dans chaque matrice de Toeplitz, chaque diagonale descendante de gauche à droite est constante. Les matrices de Toeplitz que nous utilisons ici sont également des matrices sparses.

Étant donné le premier noyau $\boldsymbol{a}^{(1)}$ et le vecteur d’entrée $\boldsymbol{x}$, la première entrée dans la sortie donnée par cette couche est, $a_1^{(1)} x_1 + a_2^{(1)} x_2 + a_3^{(1)}x_3$. Par conséquent, le vecteur de sortie entier ressemble à ce qui suit :

\[\begin{bmatrix} \mathbf{a}^{(1)}x[1:3]\\ \mathbf{a}^{(1)}x[2:4]\\ \mathbf{a}^{(1)}x[3:5]\\ \vdots \end{bmatrix}\]

La même méthode de multiplication matricielle peut être appliquée sur les couches convolutionnelles suivantes avec d’autres noyaux (par exemple $\boldsymbol{a}^{(2)}$ et $\boldsymbol{a}^{(3)}$) pour obtenir des résultats similaires.

Écouter les convolutions - Notebook Jupyter

La version anglaise du notebook Jupyter se trouve ici, la version française est disponible là.

Dans ce notebook, nous allons explorer la convolution en tant que produit scalaire courant.

La bibliothèque librosa nous permet de charger le clip audio $\boldsymbol{x}$ et son taux d’échantillonnage. Dans ce cas, il y a $70 641$ échantillons, le taux d’échantillonnage est de $22,05$kHz et la durée totale du clip est de $3.2$s. Le signal audio importé est ondulé (voir la figure 1) et nous pouvons deviner à quoi il ressemble d’après l’amplitude de l’axe $y$. Le signal audio $x(t)$ est en fait le son joué lorsque le système Windows s’éteint (voir la figure 2).

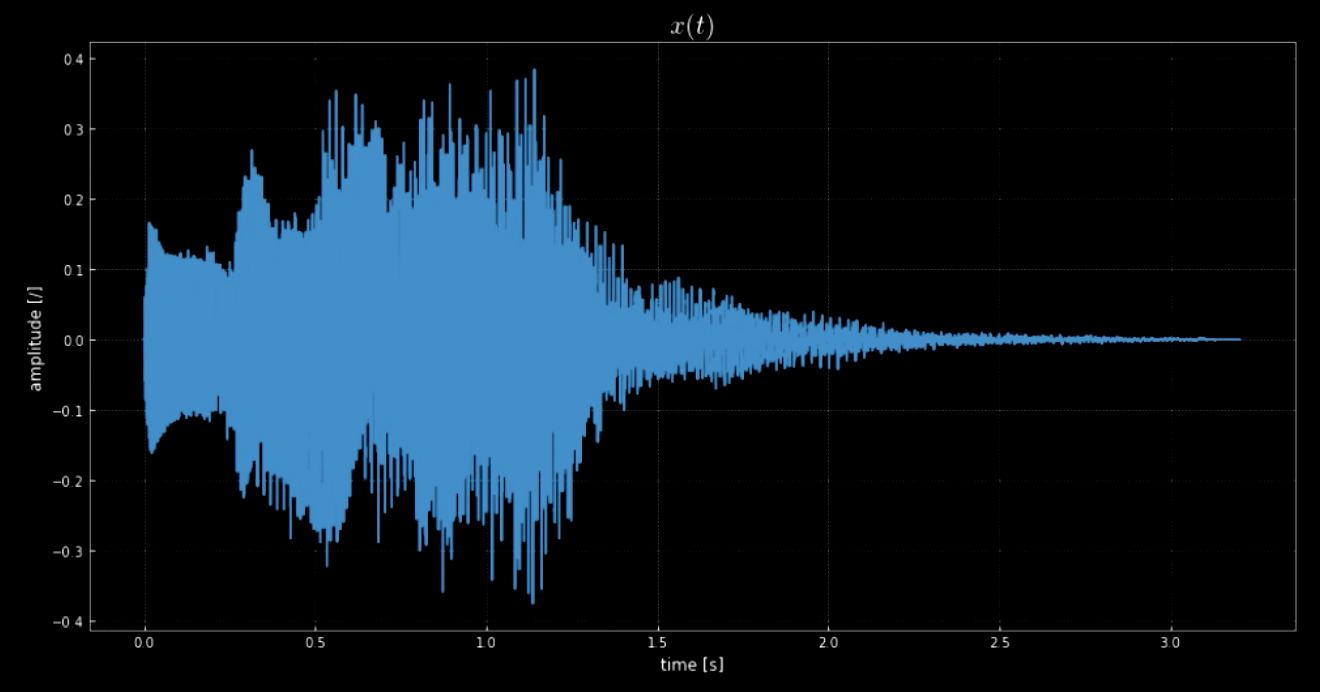
Figure 1 : Une visualisation du signal audio.

Figure 2 : Notes pour le signal audio ci-dessus

Nous devons séparer les notes de la forme de l’onde. Pour y parvenir, si nous utilisons la transformée de Fourier (FT), toutes les notes sortiront ensemble et il sera difficile de déterminer le moment et l’emplacement exacts de chaque hauteur. C’est pourquoi il est nécessaire d’utiliser une transformée de Fourier localisée (également appelée spectrogramme). Comme on peut l’observer dans le spectrogramme (voir la figure 3), les différentes hauteurs de son culminent à des fréquences différentes (par exemple, la première hauteur de son culmine à $1600$). En concaténant les quatre hauteurs à leurs fréquences, on obtient une version à hauteur du signal original.

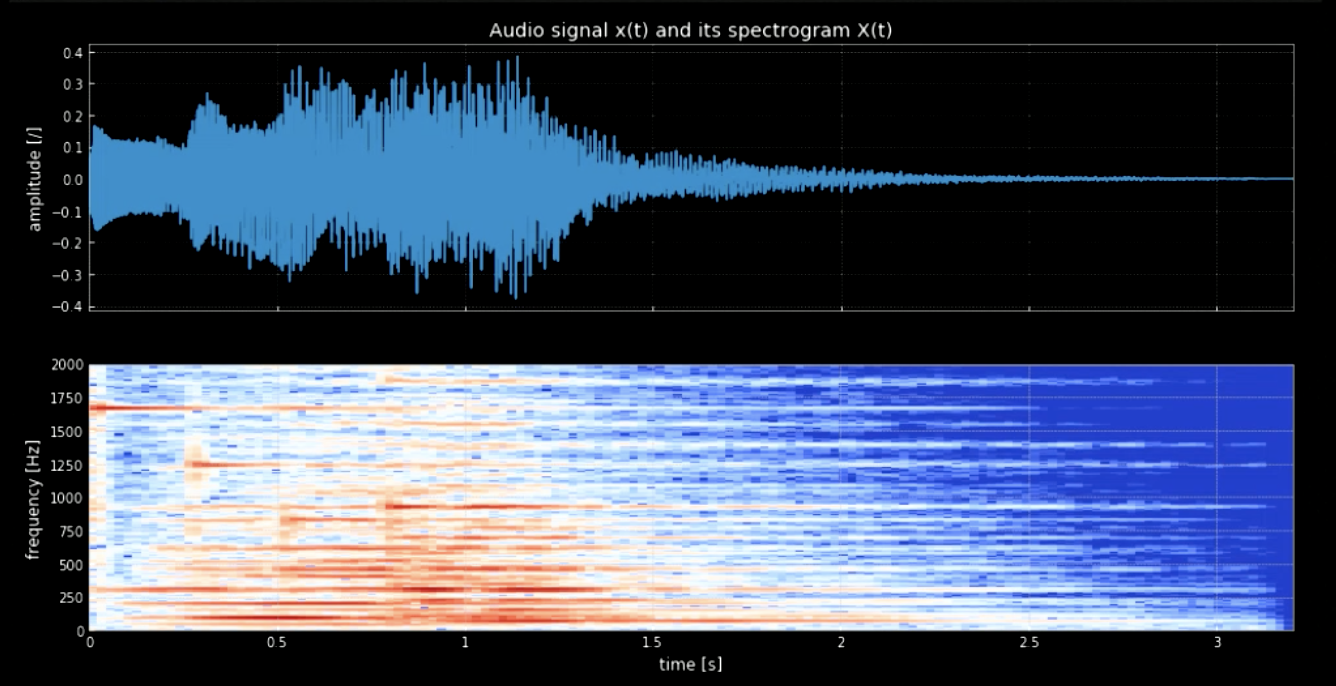
Figure 3 : Signal audio et son spectrogramme

La convolution du signal d’entrée avec toutes les hauteurs (toutes les touches du piano par exemple) peut aider à extraire toutes les notes du morceau d’entrée (c’est-à-dire les coups lorsque l’audio correspond aux noyaux spécifiques). Les spectrogrammes du signal original et du signal des hauteurs concaténées sont illustrés à la figure 4, tandis que les fréquences du signal original et des quatre hauteurs sont illustrées à la figure 5. Le tracé des convolutions des quatre noyaux avec le signal d’entrée (signal original) est illustré à la figure 6. La figure 6 ainsi que les clips audios des convolutions prouvent l’efficacité des convolutions dans l’extraction des notes.

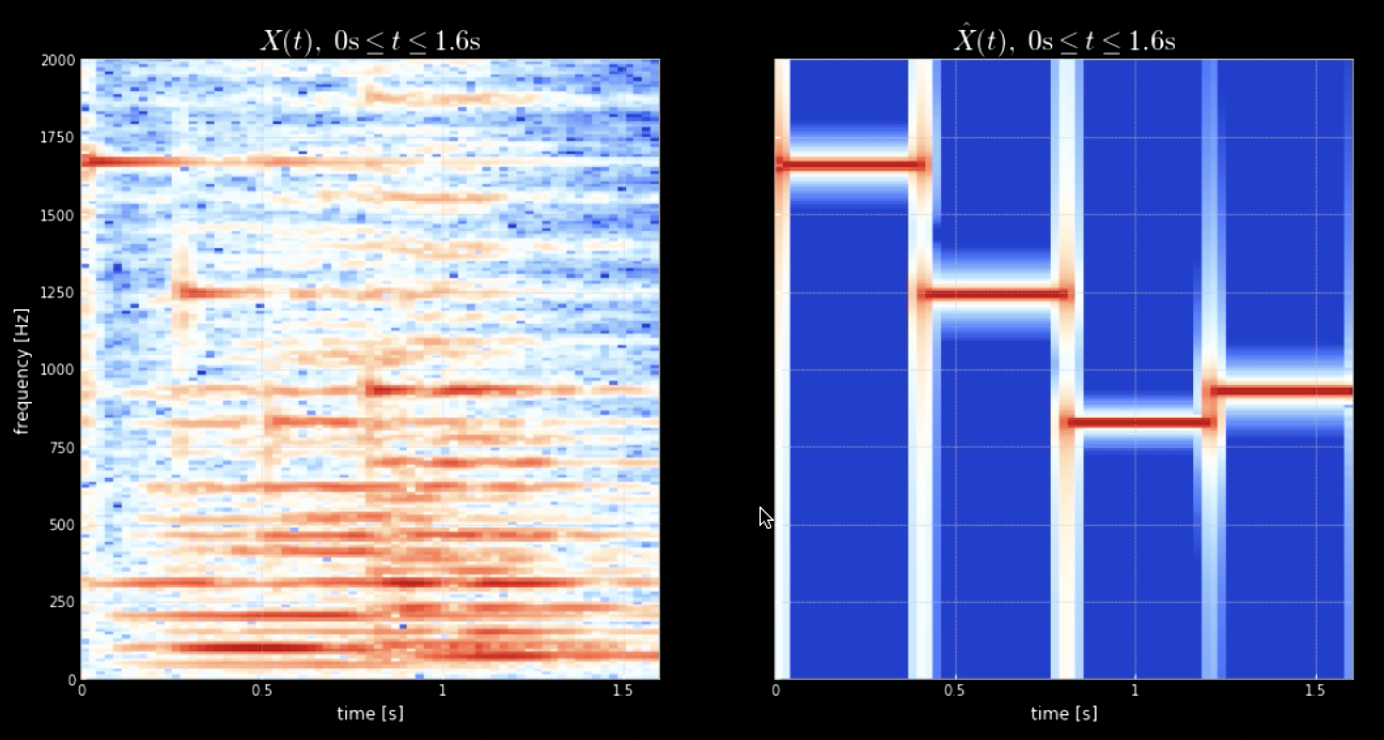
Figure 4 : Spectrogramme du signal original (à gauche) et Spectrogramme de la concaténation des hauteurs (à droite)

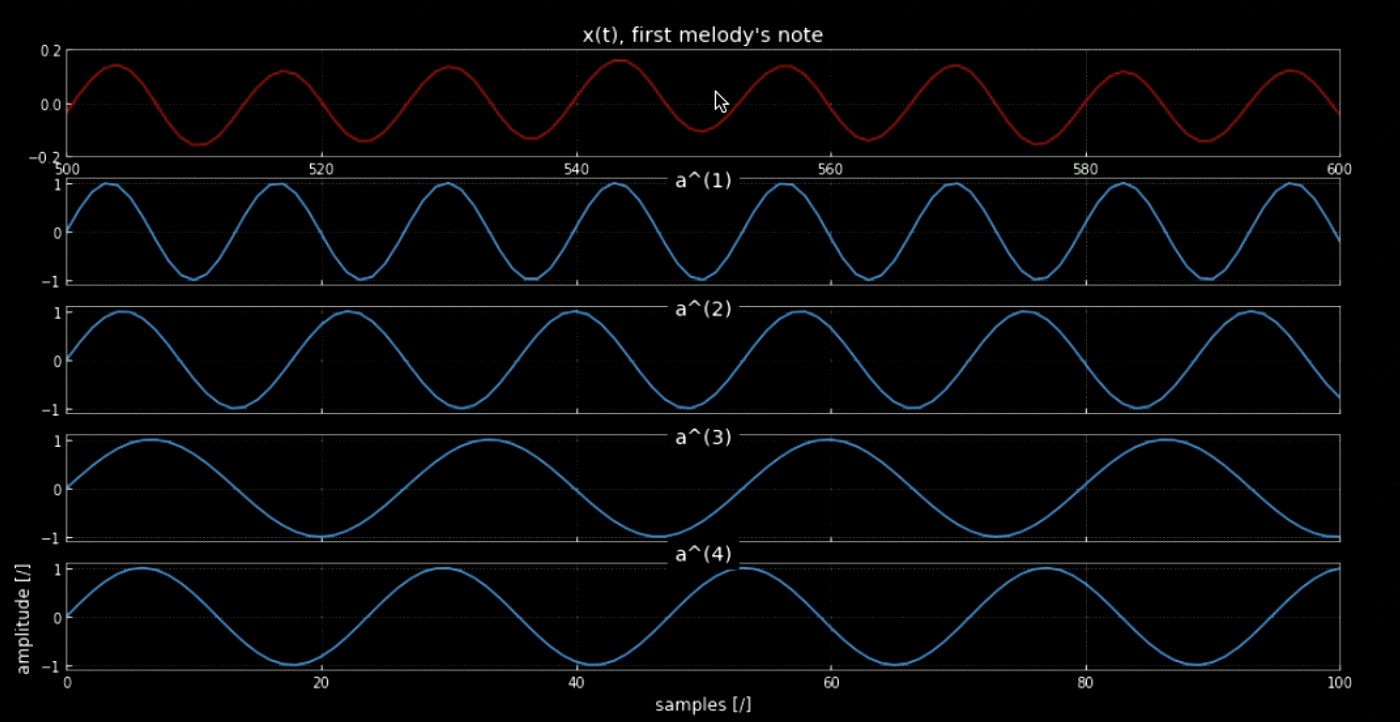
Figure 5 : Première note de la mélodie

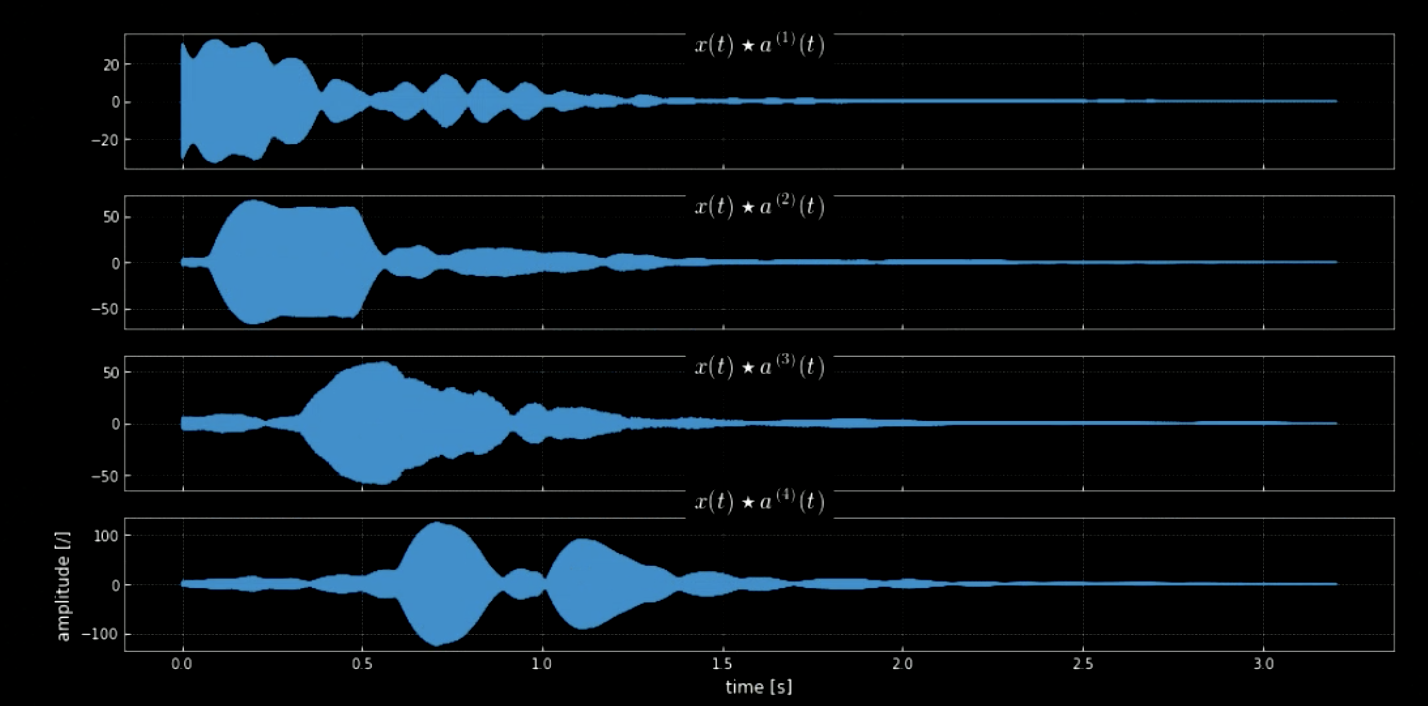
Figure 6 : Convolution de quatre noyaux

Dimensionnalité des différents jeux de données

La dernière partie est une courte digression sur les différentes représentations de la dimensionnalité et des exemples pour celle-ci. Nous considérons ici que l’ensemble d’entrée $X$ est constitué de fonctions de cartographie des domaines $\Omega$ aux canaux $c$.

Exemples

• Données audios : le domaine est 1D, signal discret indexé par le temps. Le nombre de canaux $c$ peut varier entre différentes possibilités : 1 (mono), 2 (stéréo), 5+1 (Dolby 5.1), etc.
• Données d’image : le domaine est 2D (pixels) et le $c$ peut varier entre 1 (niveaux de gris), 3 (couleur), 20 (hyperspectral), etc.
• Relativité spéciale : le domaine est $\mathbb{R^4} \times \mathbb{R^4}$ (espace-temps $\times$ quatre-momentum). Quand $c = 1$ on dit Hamiltonien.

Figure 7 : Différentes dimensions de différents types de signaux

---

📝 Yuchi Ge, Anshan He, Shuting Gu, and Weiyang Wen
Loïck Bourdois
18 Feb 2020