Introduction aux auto-encodeurs

Application des auto-encodeurs

Génération d’images

Pouvez-vous dire quel visage est faux dans la figure 1 ? En fait, les deux sont produits par le générateur StyleGan2. Bien que les détails du visage soient très réalistes, l’arrière-plan semble bizarre (à gauche : flou, à droite : objets déformés). Cela s’explique par le fait que le réseau neuronal est entraîné sur des échantillons de visages. L’arrière-plan présente alors une variabilité beaucoup plus importante. Ici, la variété des données a environ 50 dimensions, ce qui équivaut aux degrés de liberté d’une image de visage.

Figure 1 : Visages générés à partir de StyleGan2

Différence d’interpolation dans l’espace des pixels et l’espace latent

Figure 2 : Un chien et un oiseau

Si nous interpolons linéairement entre l’image du chien et celle de l’oiseau (figure 2) dans l’espace des pixels, nous obtenons une superposition de deux images en fondu dans la figure 3. Du haut à gauche au bas à droite, le poids de l’image du chien diminue et celui de l’image de l’oiseau augmente.

Figure 3 : Résultats après interpolation

Si nous interpolons sur deux représentations de l’espace latent et les transmettons au décodeur, nous obtenons la transformation du chien en l’oiseau visible sur la figure 4.

Figure 4 : Résultats après passage dans le décodeur

De toute évidence, l’espace latent est plus efficace pour saisir la structure d’une image.

Exemples de transformation

Figure 5 : Zoom

Figure 6 : Décalage

Figure 7 : Luminosité

Figure 8 : Rotation (la rotation peut être en 3D)

Image en super-résolution

Ce modèle vise à améliorer les images et à reconstruire les visages originaux. De gauche à droite sur la figure 9, la première colonne est l’image d’entrée 16x16, la deuxième est ce que nous obtenons avec une interpolation bicubique standard, la troisième est la sortie générée par le réseau neuronal, et à droite est la véritable image.

Figure 9 : Reconstitution des visages originaux

D’après les images de sortie, il est clair qu’il existe des biais dans les données d’entraînement, ce qui rend les visages reconstruits inexacts. Par exemple, l’homme asiatique en haut à gauche a l’air européen dans les images de sortie en raison du déséquilibre des images d’entraînement. Le visage reconstruit en bas à gauche est bizarre en raison de l’absence d’images sous cet angle dans les données d’entraînement.

Images non complètes

Figure 10 : Placement d'une tache grise sur les visages

En plaçant une tache grise sur le visage, comme sur la figure 10, on éloigne l’image de la variété d’entraînement. La reconstruction du visage de la figure 11 est réalisée en trouvant l’échantillon d’image le plus proche sur la variété d’entraînement via la minimisation de la fonction énergie.

Figure 11 : Image reconstruite à partir de la figure 10

Génération d’images d’après une légende

Figure 12 : Exemple de génération d’images d’après une légende

La traduction en image de la description textuelle de la figure 12 est réalisée en extrayant les représentations des caractéristiques textuelles associées à des informations visuelles importantes, puis en les décodant en images.

Qu’est-ce qu’un auto-encodeur ?

Les auto-encodeurs sont des réseaux de neurones artificiels, entraînés de manière non supervisée, qui visent à apprendre d’abord les représentations codées de nos données et ensuite à générer les données d’entrée (aussi proches que possible) à partir des représentations codées apprises. Ainsi, la sortie d’un auto-encodeur est sa prédiction pour l’entrée.

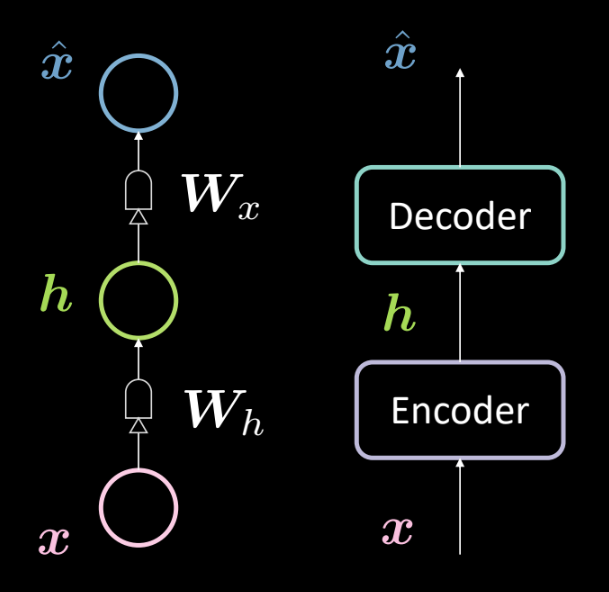
Figure 13 : Architecture d'un auto-encodeur de base

La figure 13 montre l’architecture d’un auto-encodeur de base. Comme précédemment, nous partons du bas avec l’entrée $\boldsymbol{x}$ qui est soumise à un encodeur (transformation affine définie par $\boldsymbol{W_h}$, suivie d’un écrasement). Il en résulte la couche cachée intermédiaire $\boldsymbol{h}$. Celle-ci est soumise au décodeur (une autre transformation affine définie par $\boldsymbol{W_x}$, suivie d’un autre écrasement). Cela produit la sortie $\boldsymbol{\hat{x}}$, qui est la prédiction/reconstruction de l’entrée par notre modèle.

Nous pouvons représenter mathématiquement le réseau ci-dessus en utilisant les équations suivantes :

Nous précisons également les dimensions suivantes :

Note : Pour représenter l’ACP, nous pouvons avoir des poids serrés (ou des poids liés) définis par le symbole $\boldsymbol{W_x}\ \dot{=}\ \boldsymbol{W_h}^\top$

Pourquoi utilisons-nous des auto-encodeurs ?

Les principales applications d’un auto-encodeur sont la détection d’anomalies ou le débruitage d’images. Nous savons que la tâche d’un auto- encodeur est de reconstruire des données qui vivent sur la variété, c’est-à-dire que si nous avons une variété de données, nous voudrions que notre auto-encodeur ne puisse reconstruire que l’entrée qui existe dans cette variété. Ainsi, nous contraignons le modèle à reconstruire les choses qui ont été observées pendant l’entraînement et donc toute variation présente dans les nouvelles entrées sera supprimée car le modèle est insensible à ce genre de perturbations.

Une autre application de l’auto-encodeur est la compression d’images. Si nous avons une dimension intermédiaire $d$ inférieure à la dimension d’entrée $n$, alors l’encodeur peut être utilisé comme un compresseur et les représentations cachées (représentations codées) traitent toutes (ou la plupart) des informations de l’entrée spécifique en prenant moins de place.

Perte de reconstruction

Examinons maintenant les pertes liées à la reconstruction que nous utilisons généralement avec les auto-encodeurs. La perte globale pour le jeu de données est donnée comme la perte moyenne par échantillon, c’est-à-dire :

Lorsque l’entrée est catégorielle, nous pouvons utiliser la perte d’entropie-croisée pour calculer la perte par échantillon qui est donnée par :

Et lorsque l’entrée est évaluée en valeur réelle, nous pouvons utiliser la perte d’erreur moyenne au carré donnée par :

Couche cachée sous/sur-complète

Lorsque la dimensionnalité de la couche cachée $d$ est inférieure à la dimensionnalité de l’entrée $n$, on dit que la couche cachée est sous-complète. Et de même, lorsque $d>n$, nous disons qu’il s’agit d’une couche cachée sur-complète. La figure 14 montre une couche cachée sous-complète à gauche et une couche cachée sur-complète à droite.

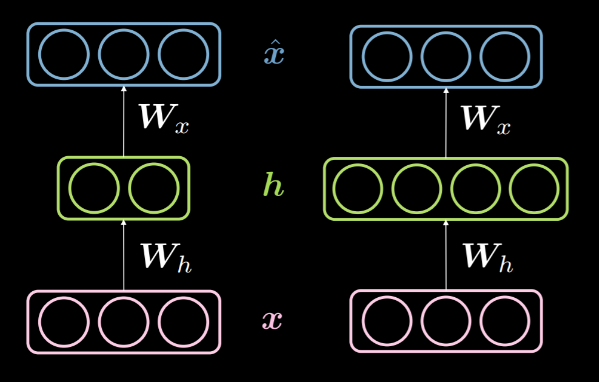
Figure 14 : Une couche cachée sous-complète vs une couche cachée sur-complète

Comme nous l’avons vu plus haut, une couche cachée sous-complète peut être utilisée pour la compression car nous encodons les informations provenant de l’entrée en moins de dimensions. En revanche, dans une couche sur-complète, nous utilisons un codage de dimension plus élevée que l’entrée. Cela facilite l’optimisation.

Comme nous essayons de reconstruire l’entrée, le modèle est enclin à copier toutes les caractéristiques d’entrée dans la couche cachée et à la faire passer comme sortie, se comportant ainsi essentiellement comme une fonction identité. Cela doit être évité car cela impliquerait que notre modèle n’apprend rien. Nous devons donc appliquer des contraintes supplémentaires en créant un goulot d’étranglement au niveau de l’information. Nous le faisons en limitant les configurations possibles que la couche cachée peut prendre aux seules configurations vues pendant l’entraînement. Cela permet une reconstruction sélective (limitée à un sous-ensemble de l’espace d’entrée) et rend le modèle insensible à tout ce qui ne se trouve pas dans la variété.

Il est à noter qu’une couche sous-complète ne peut pas se comporter comme une fonction d’identité simplement parce que la couche cachée n’a pas assez de dimensions pour copier l’entrée. Ainsi, une couche cachée sous-complète a moins de chances de faire du surentraînement qu’une couche cachée sur-complète. Néanmoins elle peut quand même en faire. Par exemple, avec un encodeur et un décodeur puissants, le modèle pourrait simplement associer un numéro à chaque point de données et apprendre l’association. Il existe plusieurs méthodes pour éviter le surentraînement, telles que les méthodes de régularisation, les méthodes architecturales, etc.

Auto-encodeur débruiteur

La figure 15 montre les multiples possibilités de l’auto-encodeur débruiteur et l’intuition de son fonctionnement.

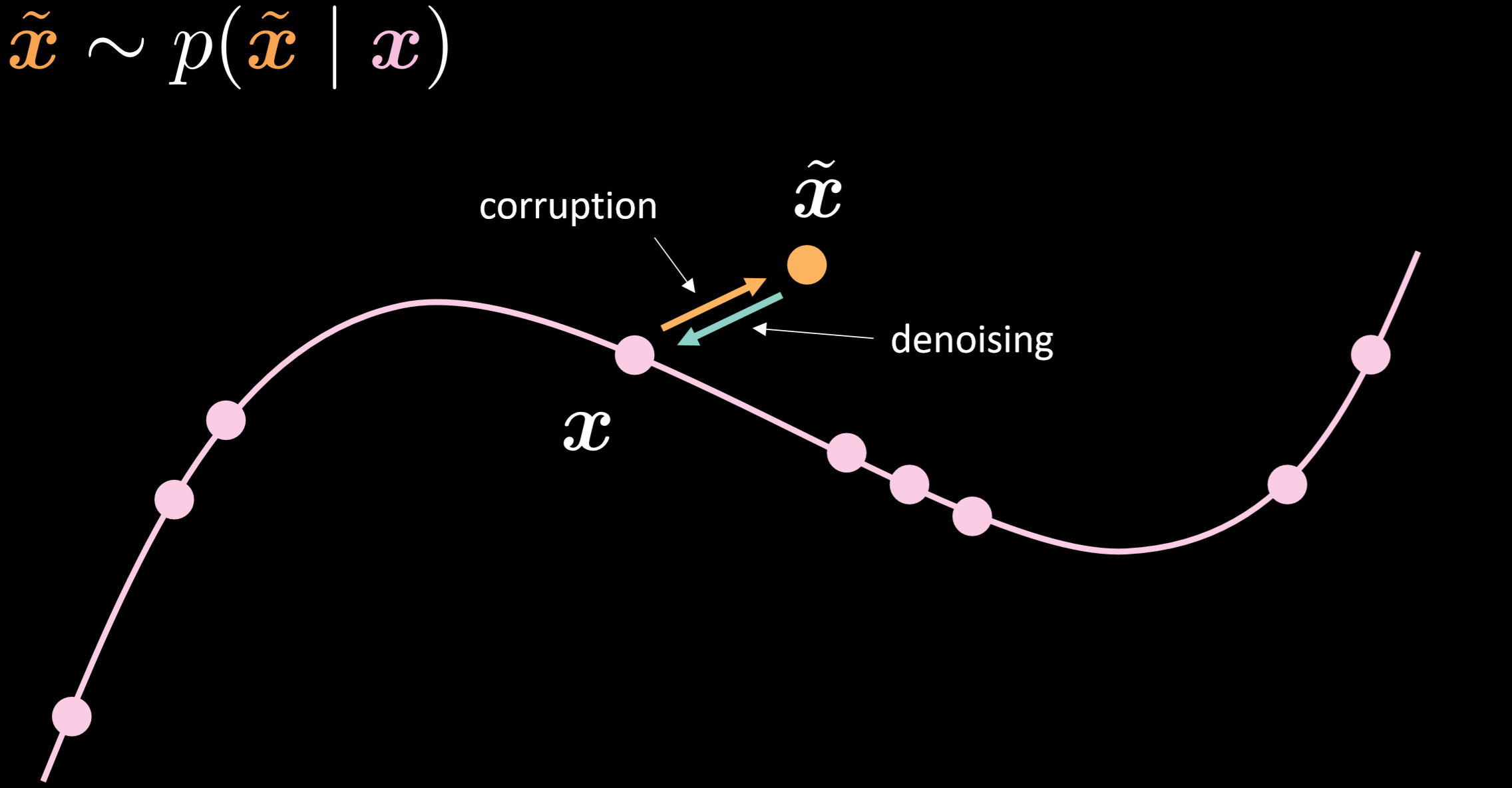
Figure 15 : Auto-encodeur débruiteur

Dans ce modèle, nous supposons que nous injectons la même distribution bruitée que celle que nous allons observer dans la réalité, afin que nous puissions apprendre à nous en remettre de manière robuste. En comparant l’entrée et la sortie, nous pouvons dire que les points qui se trouvaient déjà sur la variété des données n’ont pas bougé et que les points qui étaient éloignés sur la variété ont beaucoup bougé.

La figure 16 présente la relation entre les données d’entrée et les données de sortie.

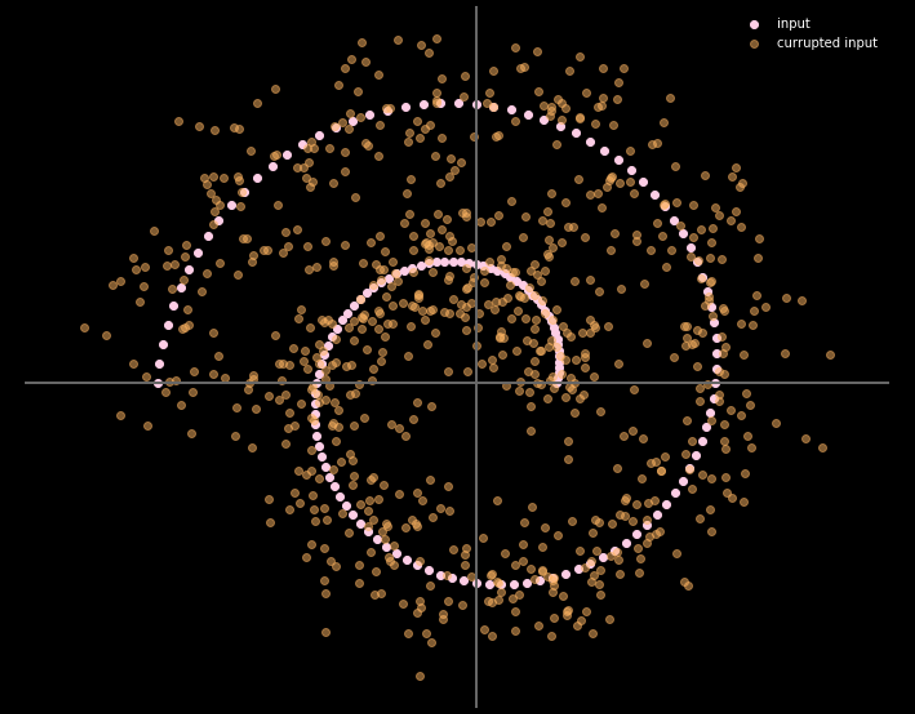
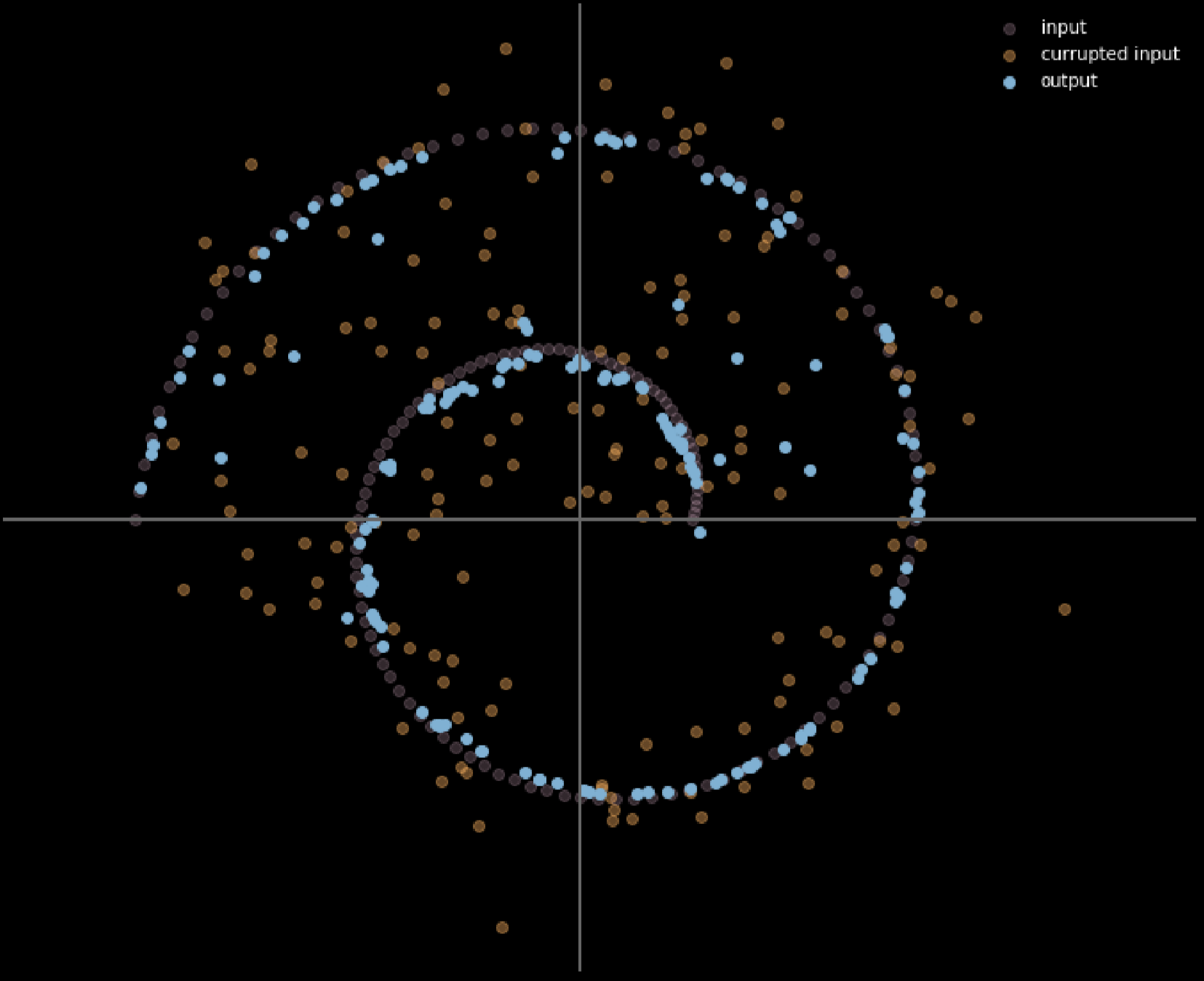
Figure 16 : Entrée et sortie de l'auto-encodeur débruiteur

Nous pouvons utiliser différentes couleurs pour représenter la distance de chaque mouvement de point d’entrée, la figure 17 montre le diagramme.

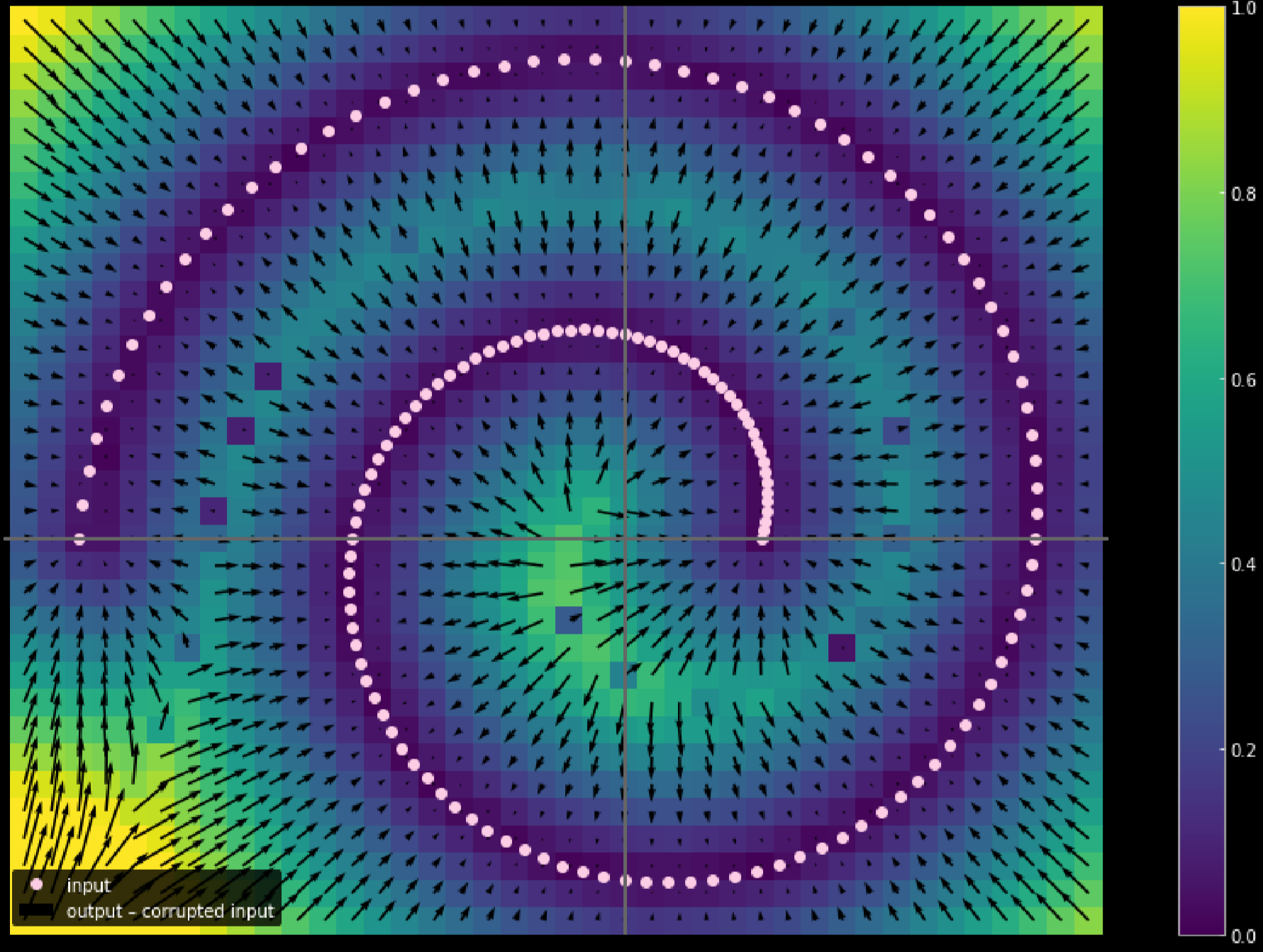
Figure 17 : Mesure de la distance parcourue par les données d'entrée

Plus la couleur est claire, plus la distance parcourue par un point est longue. D’après le diagramme, nous pouvons dire que les points aux coins ont parcouru une distance proche d’une unité, alors que les points à l’intérieur des deux branches n’ont pas bougé du tout puisqu’ils sont attirés par les branches supérieures et inférieures pendant le processus d’entraînement.

Auto-encoder contractif

La figure 18 montre la fonction de perte de l’auto-encodeur contractif et de la variété.

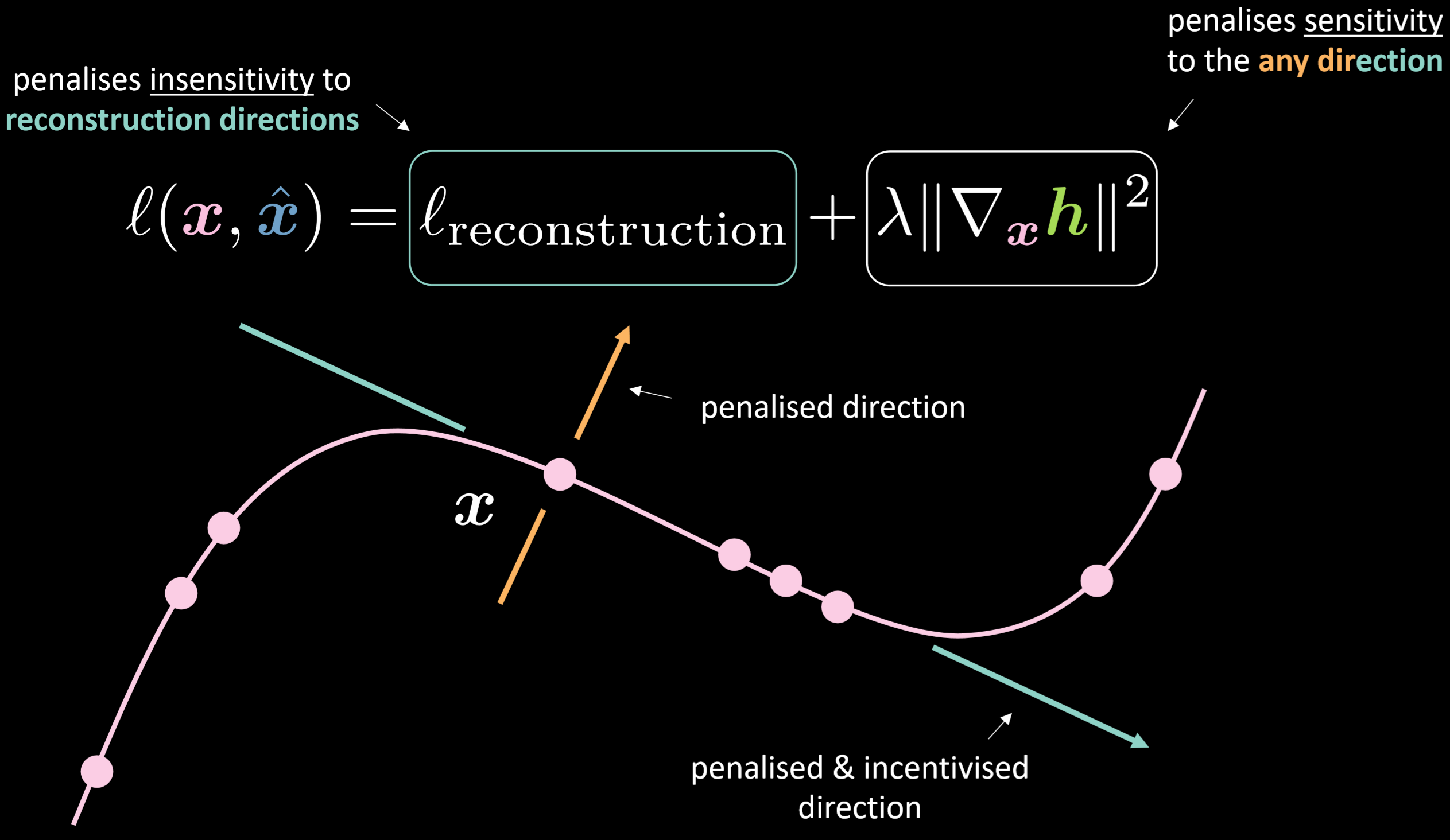
Figure 18 : Auto-encodeur contractif

La fonction de perte contient le terme de reconstruction plus la norme au carré du gradient de la représentation cachée par rapport à l’entrée. Par conséquent, la perte globale minimise la variation de la couche cachée compte tenu de la variation de l’entrée. L’avantage est de rendre le modèle sensible aux directions de reconstruction tout en étant insensible aux autres directions possibles.

La figure 19 montre comment ces auto-encodeurs fonctionnent en général.

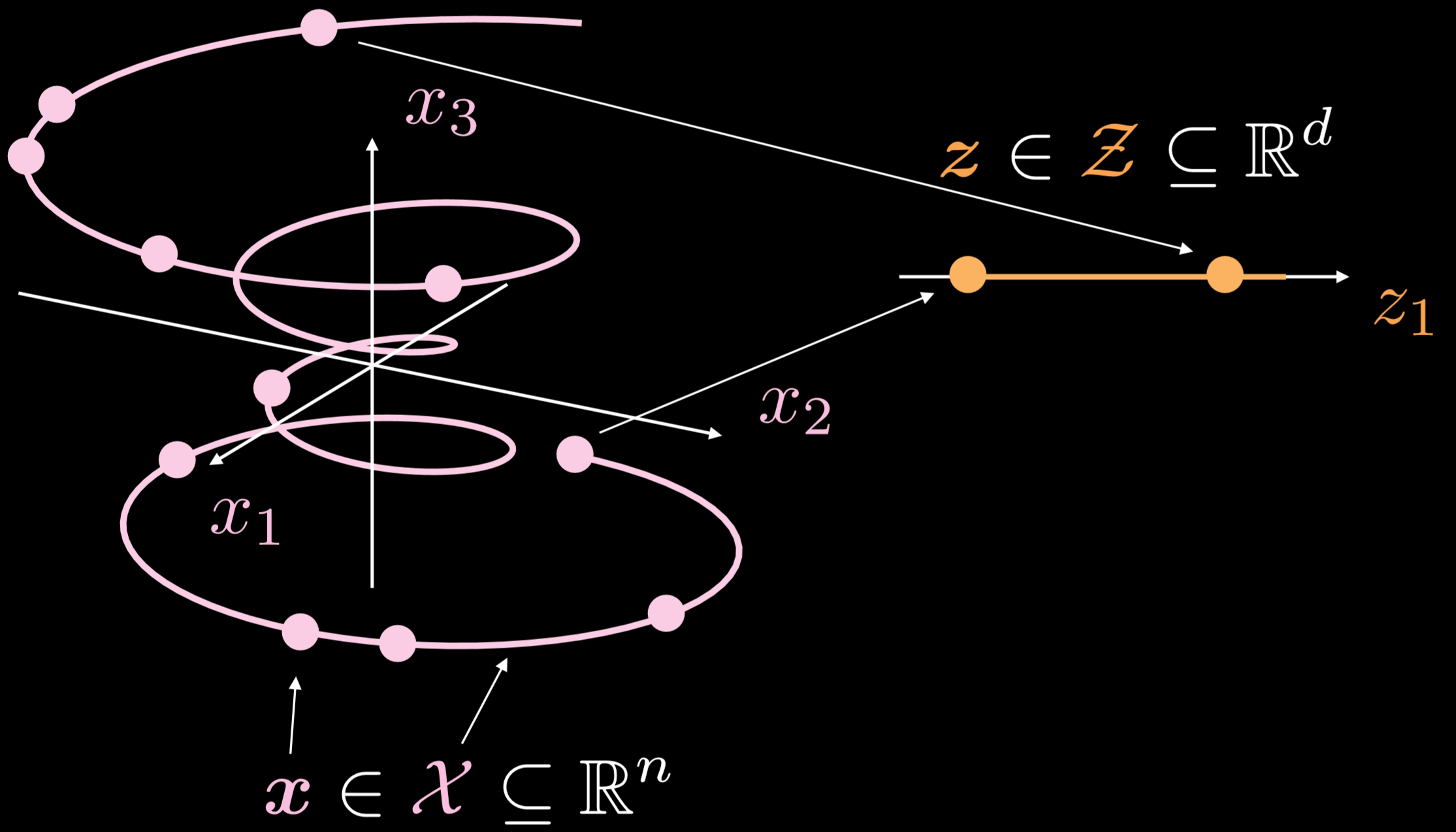
Figure 19 : Auto-encodeur standard

La variété d’entraînement est un objet unidimensionnel allant à trois dimensions. Où $\boldsymbol{x}\in \boldsymbol{X}\subseteq\mathbb{R}^{n}$, le but de l’auto-encodeur est d’étirer la ligne bouclée dans une direction, où $\boldsymbol{z}\in \boldsymbol{Z}\subseteq\mathbb{R}^{d}$. En conséquence, un point de la couche d’entrée est transformé en un point de la couche latente. Nous avons maintenant la correspondance entre les points de l’espace d’entrée et les points de l’espace latent, mais pas la correspondance entre les régions de l’espace d’entrée et les régions de l’espace latent. Ensuite, nous utilisons le décodeur pour transformer un point de la couche latente afin de générer une couche de sortie significative.

Notebook : Implémenter l’auto-encodeur

La version anglaise du notebook Jupyter se trouve ici et la version française ici.

Dans ce notebook, nous allons implémenter un auto-encodeur standard et un auto-encodeur débruiteur, puis comparer les résultats.

Définir l’architecture du modèle d’auto-encodeur et la perte de reconstruction

On utilise une image $28 \times 28$ et une couche cachée en $30$ dimensions. La routine de transformation passe de $784\to30\to784$. En appliquant la fonction tangente hyperbolique à la routine d’encodage et de décodage, nous sommes en mesure de limiter la plage de sortie à $(-1, 1)$. La perte d’erreur quadratique moyenne (MSE) est utilisée comme fonction de perte de ce modèle.

class Autoencoder(nn.Module):
    def __init__(self):
        super().__init__()
        self.encoder = nn.Sequential(
            nn.Linear(n, d),
            nn.Tanh(),
        )
        self.decoder = nn.Sequential(
            nn.Linear(d, n),
            nn.Tanh(),
        )

    def forward(self, x):
        x = self.encoder(x)
        x = self.decoder(x)
        return x

model = Autoencoder().to(device)
criterion = nn.MSELoss()

Entraîner un auto-encodeur standard

Pour entraîner un auto-encodeur standard en utilisant PyTorch, nous devons mettre les 5 méthodes suivantes dans la boucle d’entraînement :

Passe avant :

1) Envoyer l’image d’entrée à travers le modèle en appelant output = model(img).
2) Calculer la perte en utilisant : criterion(output, img.data).

Passe arrière :

3) Effacer le gradient pour s’assurer que nous n’accumulons pas la valeur : optimizer.zero_grad().
4) Rétropropagation : loss.backward()
5) étape arrière : optimizer.step()

La figure 20 montre la sortie de l’auto-encodeur standard.

Figure 20 : Sortie de l’auto-encodeur standard

Entraîner un auto-encodeur débruiteur

Pour l’auto-encodeur débruiteur, nous devons ajouter les étapes suivantes :
1) Appeler do = nn.Dropout() crée une fonction qui éteint les neurones de façon aléatoire.
2) Créer un masque de bruit : do(torch.ones(img.shape)).
3) Créez de mauvaises images en multipliant les bonnes images aux masques binaires : img_bad = (img * noise).to(device).

La figure 21 montre la sortie de l’auto-encodeur débruiteur.

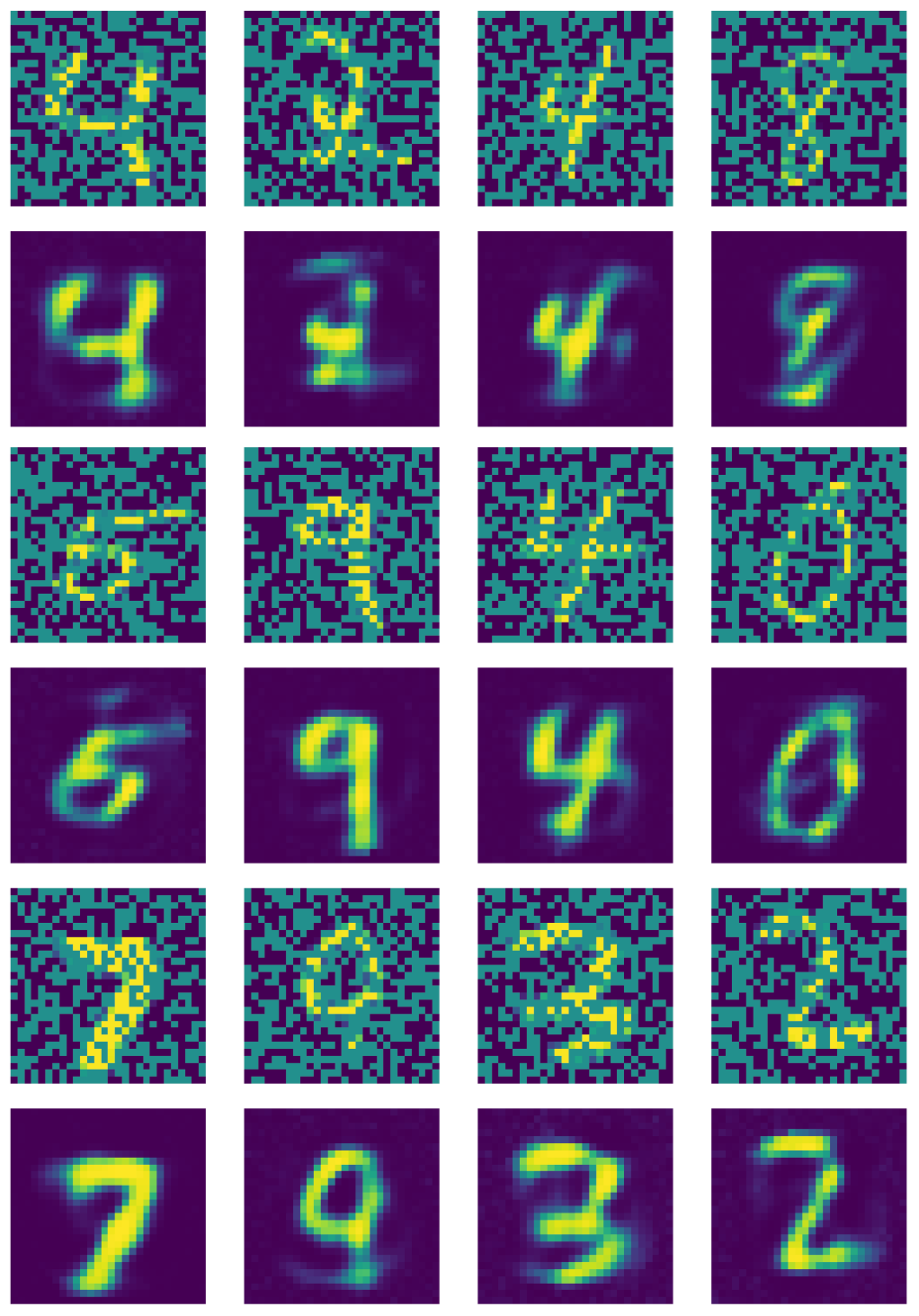
Figure 21 : Sortie de l'auto-encodeur débruiteur

Comparaison des noyaux

Il est important de noter que malgré le fait que la dimension de la couche d’entrée est de $28 \times 28 = 784$ une couche cachée d’une dimension de 500 est toujours une couche sur-complète en raison du nombre de pixels noirs dans l’image. Nous pouvons voir ci-dessous des exemples de noyaux utilisés dans un auto-encodeur standard sous-complet entraîné. Il est clair que les pixels dans la région où le nombre existe indiquent la détection d’une sorte de motif, tandis que les pixels en dehors de cette région sont essentiellement aléatoires. Cela indique que l’auto-encodeur standard ne se soucie pas des pixels situés en dehors de la région où se trouve le nombre.

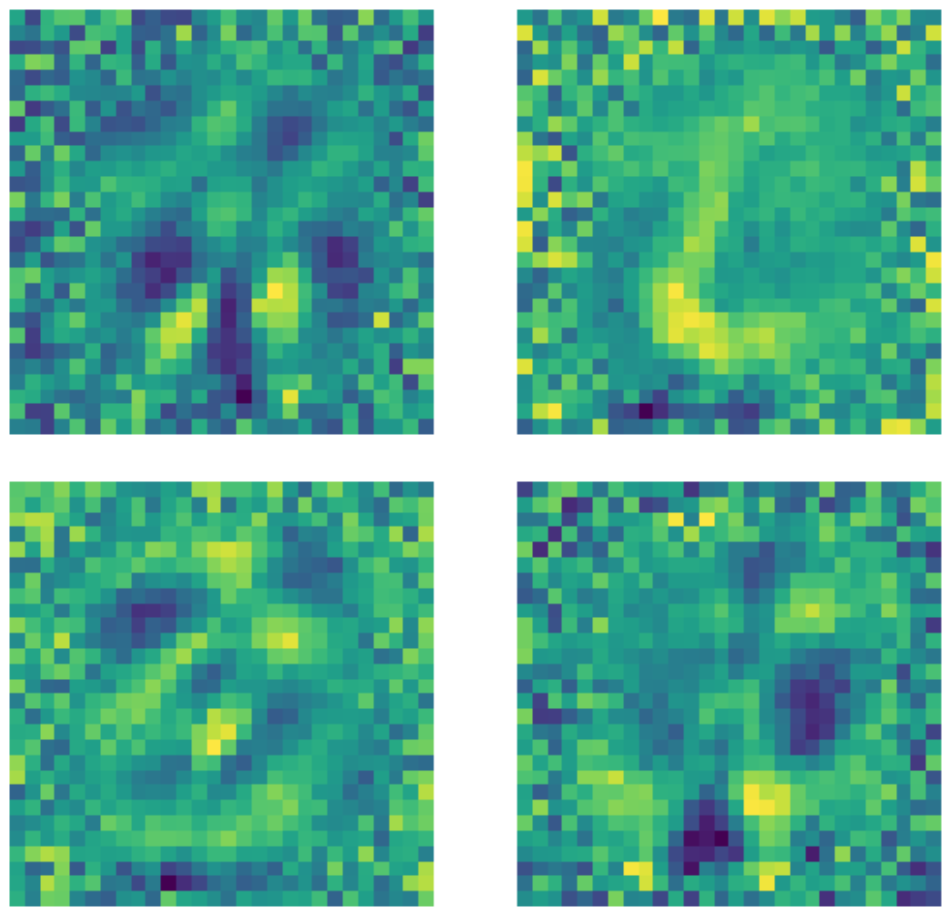
Figure 22 : Noyaux d’auto-encodeurs standards

D’autre part, lorsque les mêmes données sont transmises à un auto-encodeur débruiteur où un masque de dropout est appliqué à chaque image avant l’application du modèle, quelque chose de différent se produit. Chaque noyau qui apprend un modèle fixe les pixels en dehors de la région où le nombre existe à une certaine valeur constante. Comme un masque de dropout est appliqué aux images, le modèle se préoccupe maintenant des pixels situés en dehors de la région où le nombre existe.

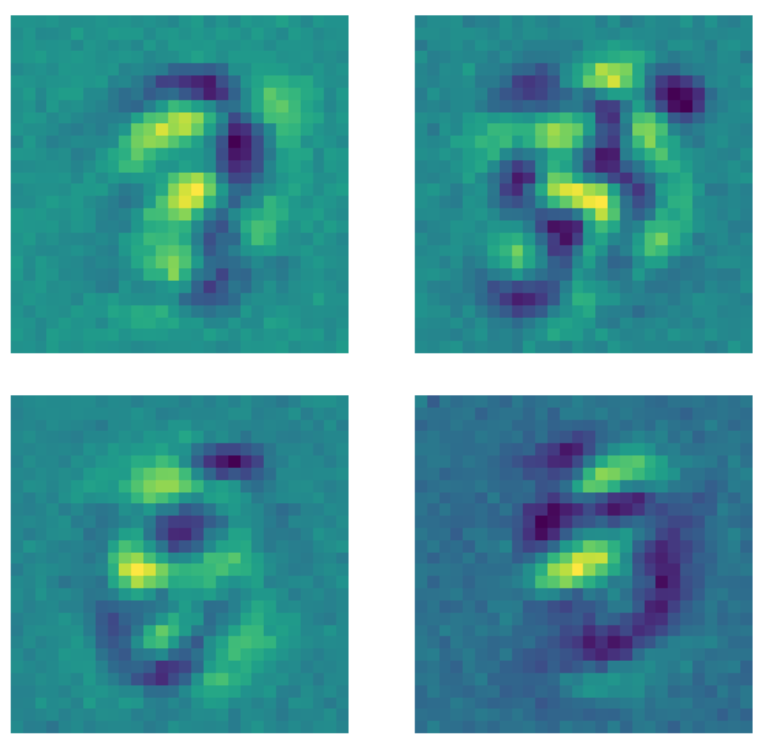
Figure 23 : Noyaux d’auto-encodeurs débruiteur

Par rapport à l’état de l’art, notre auto-encodeur fait en fait mieux ! Regardons les résultats ci-dessous :

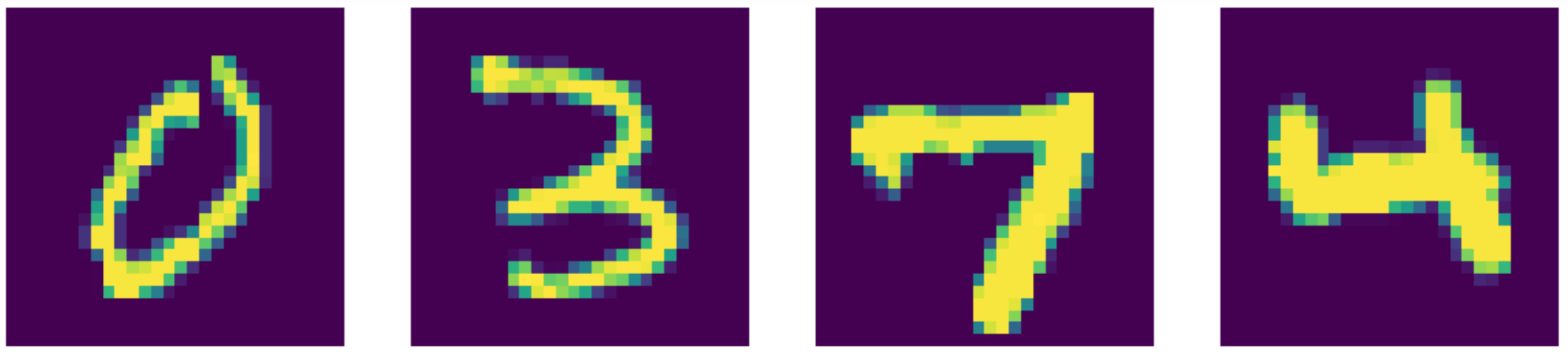
Figure 24 : Données d’entrées (MNIST)

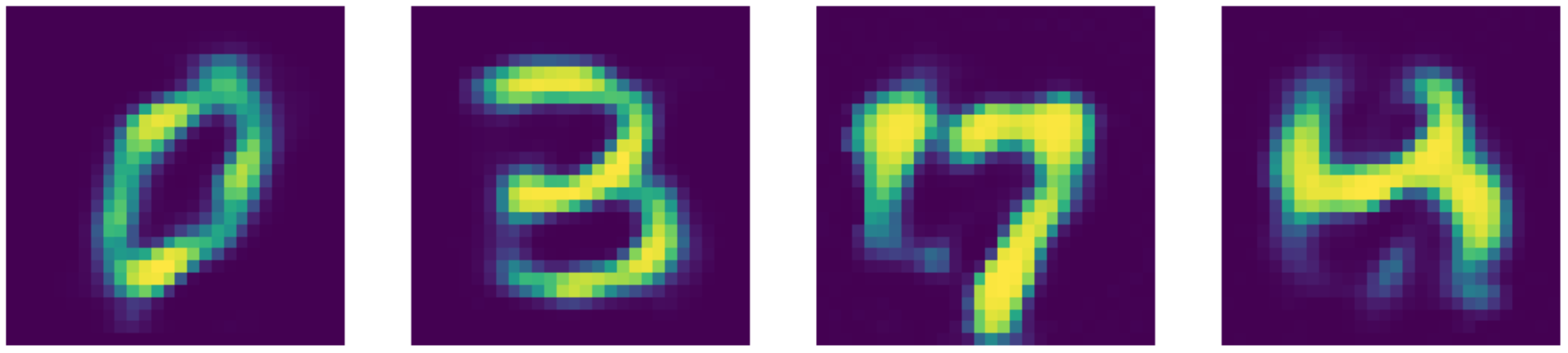
Figure 25 : Reconstructions de l'auto-encodeur débruiteur

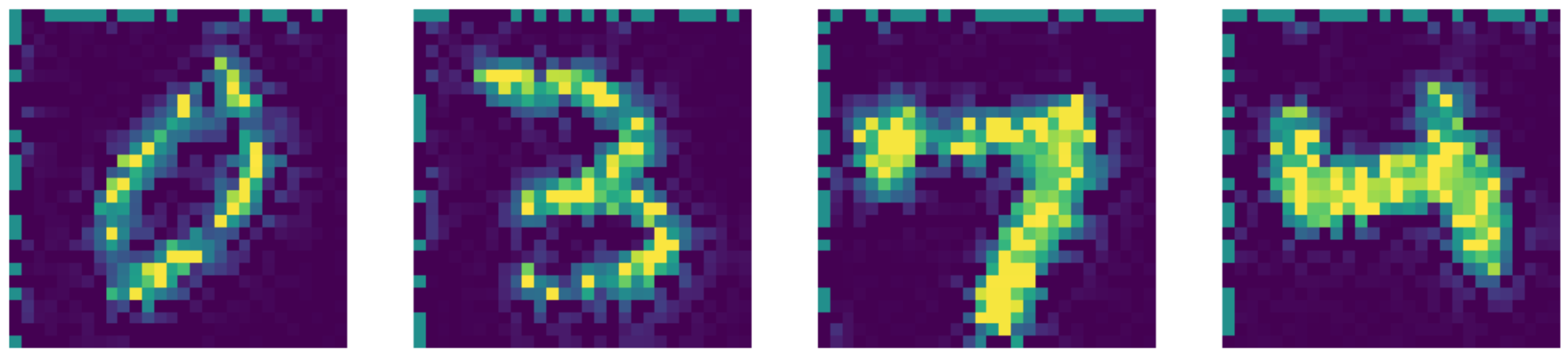
Figure 26 : Sortie obtenue via Telea

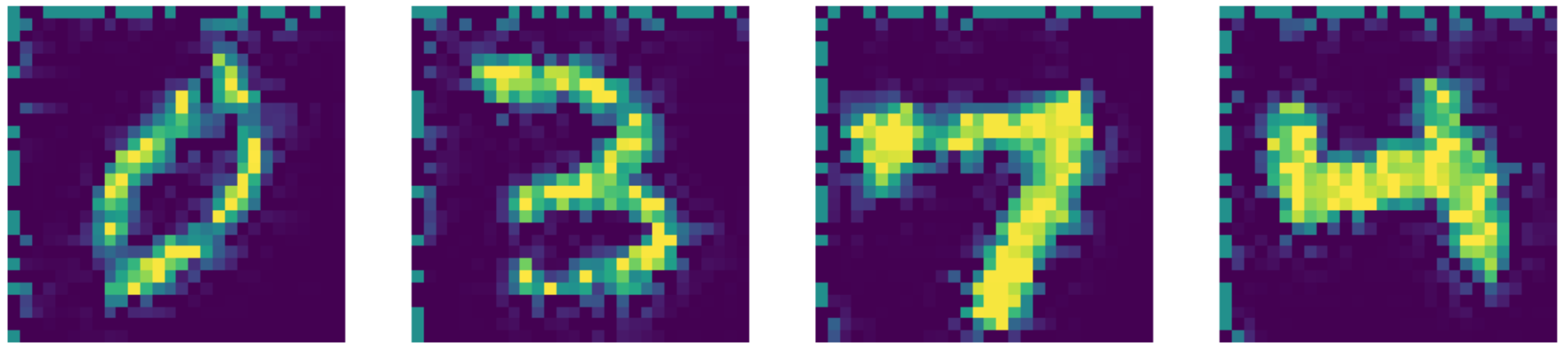
Figure 27 : Sortie obtenue via Navier-Stokes