Modèles à base d’énergie (EBMs)

Vue d’ensemble

Nous allons introduire un nouveau cadre pour la définition des modèles. Il fournit un parapluie unificateur qui aide à définir des modèles supervisés, non supervisés et autosupervisé. Les modèles à base d’énergie (EBMs) observent un ensemble de variables $x$ et produisent un ensemble de variables $y$. Les réseaux feed-forward posent deux problèmes majeurs :

1. Que faire si la procédure d’inférence est un calcul plus complexe que des couches empilées de sommes pondérées ?
2. Que faire s’il y a plusieurs résultats possibles pour une seule entrée comme par exemple la prédiction des images futures dans une vidéo ?
   Dans un réseau de classification, nous entraînons ce réseau à émettre un score pour chaque classe. Toutefois, cela n’est pas possible dans un domaine continu à haute dimension comme les images : nous ne pouvons pas avoir de softmax sur les images ! Même si la sortie est discrète, elle pourrait avoir un grand espace d’échantillonnage. Le texte est compositionnel, ce qui conduit à un grand nombre de combinaisons possibles. Les modèles basés sur l’énergie fournissent un meilleur cadre pour modéliser ces modalités.

L’approche des EBMs

Au lieu d’essayer de classer les $x$ en $y$, nous aimerions prédire si une certaine paire de ($x$, $y$) s’assemble ou non. Ou, en d’autres termes, trouver un $y$ compatible avec $x$. Nous pouvons également poser le problème de trouver un $y$ pour lequel certains $F(x,y)$ sont faibles. Par exemple :

• est-ce que $y$ est une image haute résolution précise de $x$ ?
• le texte $A$ est-il une bonne traduction du texte $B$ ?

Définition

Nous définissons une fonction énergie $F : \mathcal{X} \times \mathcal{Y} \rightarrow \mathcal{R}$ où $F(x,y)$ décrit le niveau de dépendance entre les paires $(x,y)$.
A noter que cette énergie est utilisée en inférence et non pas pour l’apprentissage. L’inférence est donnée par l’équation suivante :

Solution : l’inférence basée sur les gradients

Nous aimerions que la fonction d’énergie soit lisse et différenciable afin d’effectuer l’inférence. Nous recherchons cette fonction en utilisant la descente de gradient pour trouver des $y$ compatibles. Il existe de nombreuses méthodes alternatives aux méthodes de gradient pour obtenir le minimum.

Note : les modèles graphiques sont un cas particulier des modèles à base d’énergie. La fonction d’énergie se décompose en une somme de termes d’énergie. Chaque terme énergétique prend en compte un sous-ensemble de variables que nous avons à traiter. S’ils s’organisent sous une forme particulière, il existe des algorithmes d’inférence efficaces pour trouver le minimum de la somme des termes par rapport à la variable que nous souhaitons inférer.

EBMs à variables latentes

La sortie $y$ dépend de $x$ ainsi que d’une variable supplémentaire $z$ (la variable latente) dont nous ne connaissons pas la valeur. Ces variables latentes peuvent fournir des informations auxiliaires. Par exemple, elle peut vous indiquer la position des limites des mots dans un morceau de texte. C’est utile quand nous voulons interpréter une écriture sans espaces. C’est aussi particulièrement utile pour les discours qui peuvent présenter des lacunes difficiles à déchiffrer. De plus, certaines langues ont des limites de mots très faibles comme par exemple le français. Ainsi, la présence de cette variable latente dans notre modèle est très utile pour interpréter de telles entrées.

Inférence

Pour réaliser l’inférence d’un EBM à variable latente, nous voulons minimiser simultanément la fonction d’énergie par rapport à $y$ et $z$ :

Et cela équivaut à redéfinir la fonction énergie comme : \(F_\infty(x,y) = \text{argmin}_{z}E(x,y,z)\), ce qui équivaut à : \(F_\beta(x,y) = -\frac{1}{\beta}\log\int_z \exp(-\beta E(x,y,z))\).
Lorsque $\beta \rightarrow \infty$, alors $\check{y} = \text{argmin}_{y}F(x,y)$.

Un autre grand avantage d’autoriser des variables latentes est qu’en faisant varier la variable latente sur un ensemble, nous pouvons aussi faire varier la prédiction $y$ sur la multitude de prédictions possibles (le ruban est montré dans le graphique ci-dessous) : $F(x,y) = \text{argmin}_{z} E(x,y,z)$.

Cela permet à une machine de produire plusieurs sorties.

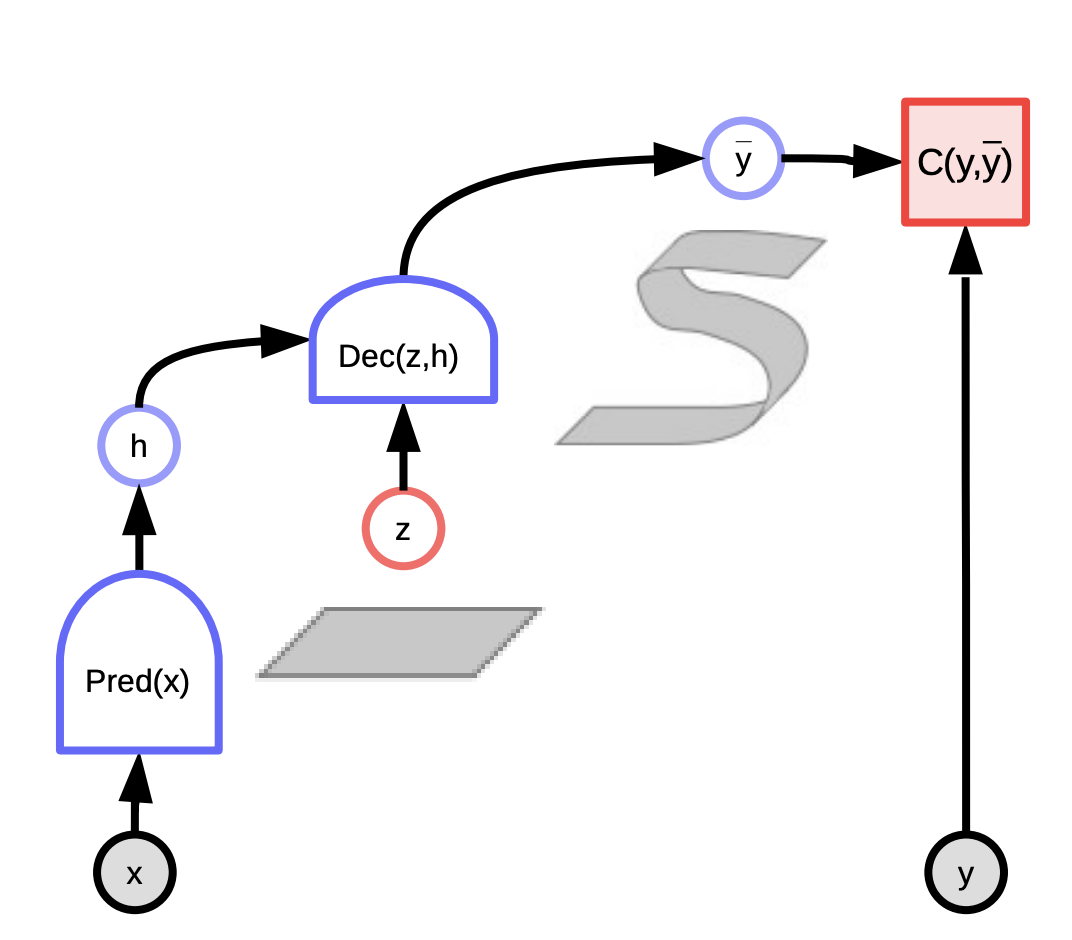
Figure 1 : Graphe de calcul pour les modèles à base d’énergie

Exemples

Un exemple est la prédiction vidéo. Il existe de nombreuses bonnes applications pour l’utilisation de la prédiction vidéo, par exemple pour la réalisation d’un système de compression vidéo. Une autre est d’utiliser la vidéo d’une voiture autonome et de prédire ce que les autres voitures vont faire.

Un autre exemple est la traduction. La traduction a toujours été un problème difficile car il n’existe pas de traduction unique et correcte d’un texte d’une langue à l’autre. En général, il existe de nombreuses façons différentes d’exprimer une même idée et les gens ont du mal à comprendre pourquoi ils en choisissent une plutôt qu’une autre. Il serait donc bon que nous ayons un moyen de paramétrer toutes les traductions possibles qu’un système pourrait produire pour un texte donné. Disons que si nous voulons traduire de l’allemand en anglais, il pourrait y avoir plusieurs traductions en anglais qui sont toutes correctes, et en faisant varier certaines variables latentes, vous pourriez alors faire varier la traduction produite.

Les EBMs vs les modèles probabilistes

Nous pouvons considérer les énergies comme des probabilités logarithmiques négatives non normalisées et utiliser la distribution de Gibbs-Boltzmann pour convertir l’énergie en probabilité après normalisation qui est :

où $\beta$ est une constante positive et doit être calibrée pour s’adapter à votre modèle.
Un plus grand $\beta$ donne un modèle plus fluctuant tandis qu’un plus petit $\beta$ donne un modèle plus lisse. En physique, $\beta$ est la température inverse : $\beta \rightarrow \infty$ signifie que la température va à 0.

Maintenant, si on marginalise sur $y$ : $P(y \mid x) = \int_z P(y,z \mid x)$, on a :

Ainsi, si nous disposons d’un modèle à variable latente et que nous voulons éliminer la variable latente $z$ de manière probabiliste, il suffit de redéfinir la fonction d’énergie $F_\beta$ : l’énergie libre.

L’énergie libre

Calculer ceci peut être très difficile. En fait, dans la plupart des cas, c’est probablement insoluble. Donc si vous avez une variable latente que vous voulez minimiser à l’intérieur de votre modèle ou si vous avez une variable latente que vous voulez marginaliser (ce que vous faites en définissant cette fonction d’énergie $F$) et que la minimisation correspond à la limite infinie $\beta$ de cette formule, alors c’est possible.

Selon la définition de $F_\beta(x, y)$ ci-dessus, $P(y \mid x)$ n’est qu’une application de la formule de Gibbs-Boltzmann et $z$ a été implicitement marginalisé à l’intérieur de celle-ci. Les physiciens appellent cela l’énergie libre, c’est pourquoi nous l’appelons $F$ (free energy en anglais). Donc $e$ est l’énergie et $F$ est l’énergie libre.

Quels sont les avantages qu’offrent les modèles à base d’énergie ?

En effet, dans les modèles basés sur les probabilités, il est aussi possible d’avoir des variables latentes qui peuvent être marginalisées.

La différence est que dans les modèles probabilistes, nous n’avons pas le choix de la fonction objectif que nous allons minimiser. Il faut rester fidèle au cadre probabiliste au sens que chaque objet qui est manipulé doit avoir une distribution normalisée (qu’il est possible d’approximer en utilisant des méthodes variationnelles, etc.).
Ce que nous voulons faire en fin de compte avec ces modèles, c’est prendre des décisions. Par exemple avec un système qui conduit une voiture et qui indique « Tourner à gauche avec une probabilité de 0,8 ou tourner à droite avec une probabilité de 0,2 », on va tourner à gauche. Le fait que les probabilités soient de 0,2 et 0,8 n’a pas d’importance. Ce que nous voulons, c’est prendre la meilleure décision, parce que nous sommes obligés de prendre une décision. Les probabilités sont donc inutiles quand nous voulons prendre des décisions.
Si nous voulons combiner la sortie d’un système automatisé avec un autre (par exemple, un système humain ou autre) et que ces systèmes n’ont pas été entraînés ensemble, mais plutôt séparément, alors ce que nous voulons, ce sont des scores calibrés pour pouvoir combiner les scores des deux systèmes afin de prendre une bonne décision. Il n’y a qu’une seule façon de calibrer les scores et c’est de les transformer en probabilités. Tous les autres moyens sont soit inférieurs, soit équivalents. Mais si on souhaite entraîner un système de bout en bout à la prise de décision, alors n’importe quelle fonction de notation utilisée est bonne, à condition qu’elle donne le meilleur score à la meilleure décision.

Les EBMs offrent beaucoup plus de choix quant à la façon de manipuler le modèle, peut-être même plus de choix sur la manière de l’entraîner ainsi que pour la fonction objectif pouvant être utilisée. Si nous insistons pour que votre modèle soit probabiliste, nous devons utiliser le maximum de vraisemblance. Il nous faut entraîner le modèle de telle manière que la probabilité qu’il donne aux données observées soit maximale. Le problème est que l’on ne peut prouver que cela fonctionne que si votre modèle est « correct » mais un modèle n’est jamais « correct ». Le statisticien Goerge Box a dit : « Tous les modèles sont faux mais certains sont utiles ». Les modèles probabilistes, en particulier ceux dans les espaces en grandes dimensions et dans les espaces combinatoires comme le texte, sont donc tous des modèles approximatifs. Ils sont tous erronés d’une certaine manière et si nous essayons de les normaliser, nous les rendons encore plus erronés. Il est donc préférable de ne pas les normaliser.

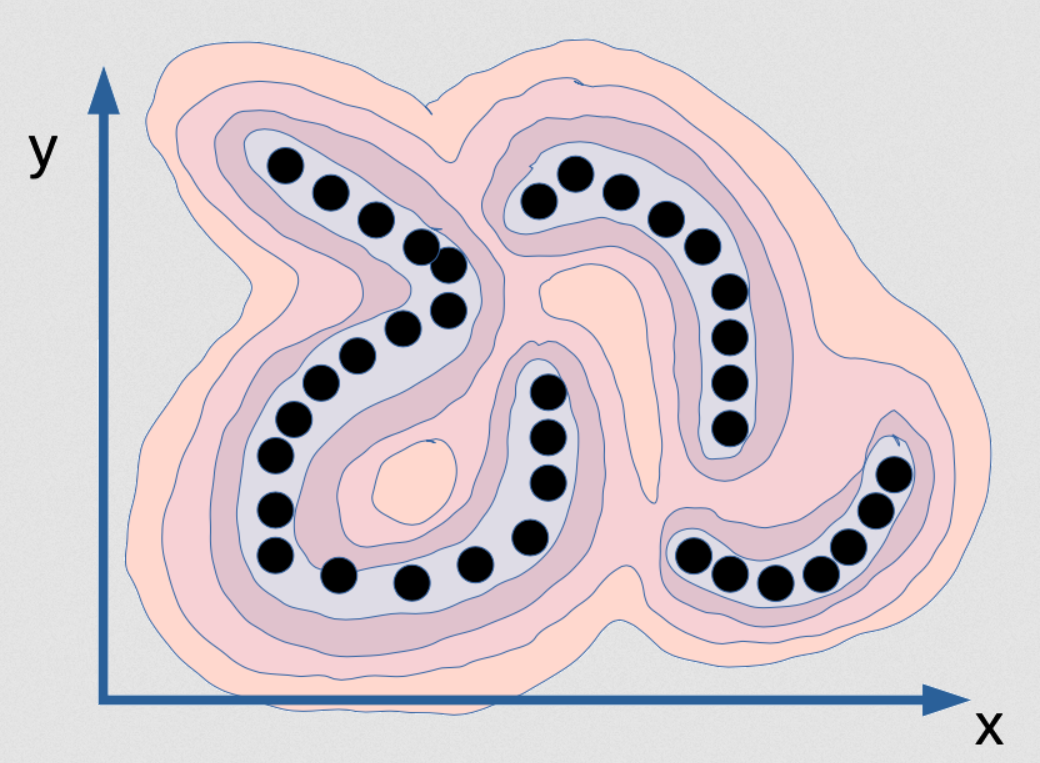
Figure 2 : Visualisation de la fonction d'énergie qui saisit la dépendance entre x et y

Il s’agit d’une fonction d’énergie qui vise à capturer la dépendance entre $x$ et $y$. C’est comme une chaîne de montagnes. Les vallées sont là où se trouvent les points noirs (ce sont des points de données) et il y a des montagnes tout autour. Considérons que les points sont sur une variété infiniment mince, la distribution des données pour les points noirs n’est donc en fait qu’une ligne, et il y en a trois. Ils n’ont aucune largeur. Donc si nous entraînons un modèle probabiliste sur cela, le modèle de densité devrait vous dire quand nous sommes sur cette surface. Sur cette variété, la densité est infinie et toutes $\varepsilon$ en dehors d’elle devrait être zéro. Ce serait le modèle correct de cette distribution. Ainsi non seulement la densité doit être infinie, mais l’intégrale sur [x et y] doit être égale à 1. C’est très difficile à mettre en œuvre sur ordinateur car c’est fondamentalement impossible. Si nous voulions calculer cette fonction par une sorte de réseau neuronal, celui-ci devra avoir des poids infinis et ils devront être calibrés de telle sorte que l’intégrale de la sortie de ce système sur l’ensemble du domaine soit de 1. C’est pratiquement impossible. Le modèle probabiliste précis et correct pour cet exemple particulier de données est impossible. C’est ce que le maximum de vraisemblance voudra que nous produisions mais aucun ordinateur au monde peut calculer ça. Donc, en fait, ce n’est même pas intéressant.
Et si nous imaginons avoir le modèle de densité parfait pour cet exemple, qui est une fine plaque dans cet espace ($x$, $y$), nous ne pourrions pas faire d’inférence ! Si on nous donne une valeur de $x$ et qu’on nous demande quelle est la meilleure valeur pour $y$, nous ne pourrions pas la trouver car toutes les valeurs de $y$, à l’exception d’un ensemble de probabilité 0, ont une probabilité de zéro et il n’y a que quelques valeurs possibles.

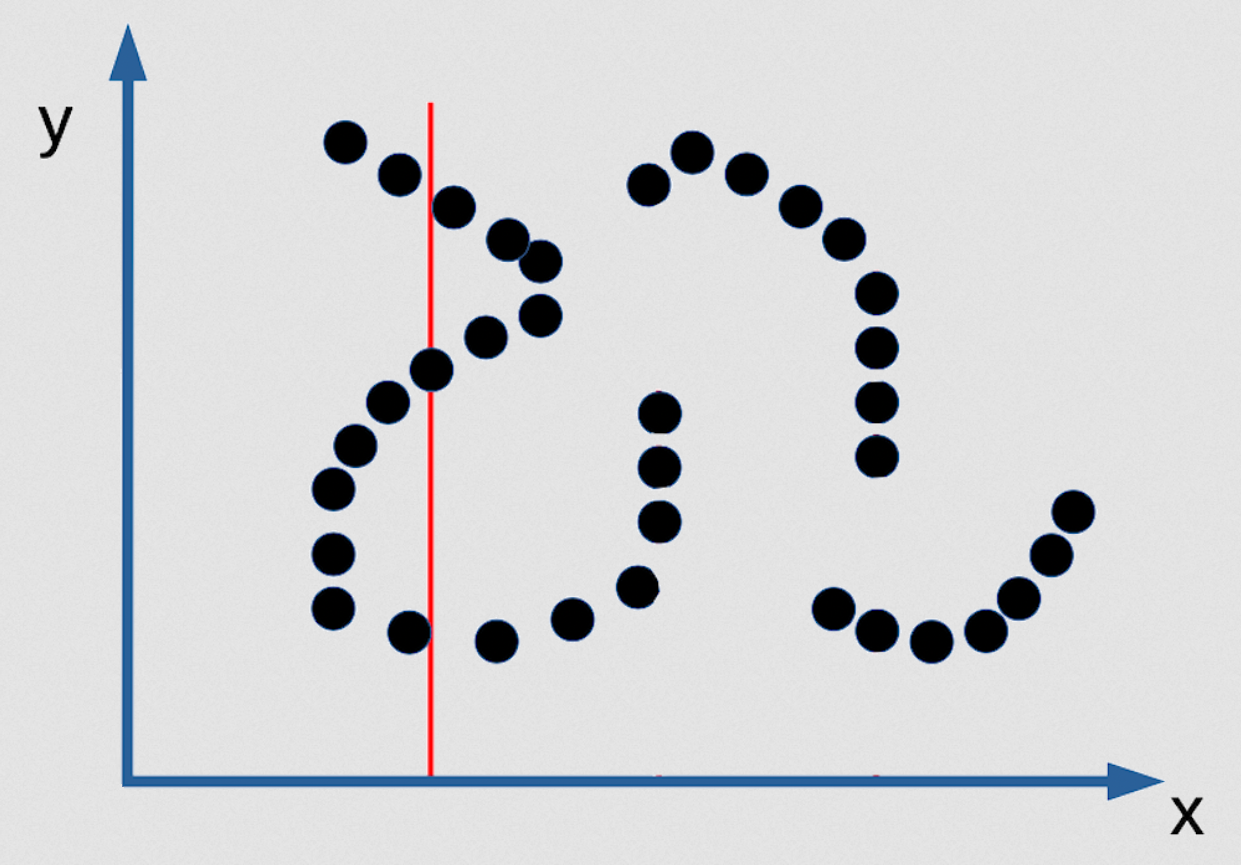
Figure 3 : Exemple de prédiction multiple de l'EBM en tant que fonction implicite

Dans la figure ci-dessous, il y a 3 valeurs de $y$ qui sont possibles pour le $x$ donné et elles sont infiniment étroites. Il n’y a pas d’algorithme d’inférence permettant de les trouver. La seule façon de faire ça est de rendre votre fonction de contraste lisse et différentiable. Alors il est possible de partir de n’importe quel point et par descente de gradient trouver une bonne valeur pour $y$ pour n’importe quelle valeur de $x$. Mais ce ne sera pas un bon modèle probabiliste de la distribution si la distribution est comme celle mentionnée. Voici donc un cas où insister pour avoir un bon modèle probabiliste est en fait mauvais. Le maximum de vraisemblance est néfaste dans ce cas !

Si vous êtes un Bayésien, vous dites « oh mais on peut corriger ça en ayant un a priori fort indiquant que la fonction de densité doit être lisse ». Mais, tout ce qui est fait en termes bayésiens (mathématiquement parlant), mène aux modèles à base d’énergie. Les EBMs qui ont un régulariseur, qui est additif à la fonction d’énergie, sont complètement équivalents aux modèles bayésiens où la vraisemblance de l’énergie est exponentielle : nous avons $\exp(\text{énergie}) \exp(\text{ régulariseur })$ et c’est égal à $\exp(\text{énergie} + \text{régulariseur})$. Supprimer l’exponentielle, donne un modèle à base d’énergie avec un régulariseur additif. Il y a donc là une correspondance entre les méthodes probabilistes et bayésiennes.