Fonction de perte et d’activation

🎙️ Yann Le Cun

Fonctions d’activation

Passons en revue certaines fonctions d’activation importantes et leurs implémentations dans PyTorch. Elles sont issues de diverses publications affirmant que ces fonctions fonctionnent mieux pour des problèmes spécifiques.

ReLU - nn.ReLU()

La fonction ReLU (Rectified Linear Unit) est définie par :

\[\text{ReLU}(x) = (x)^{+} = \max(0,x)\]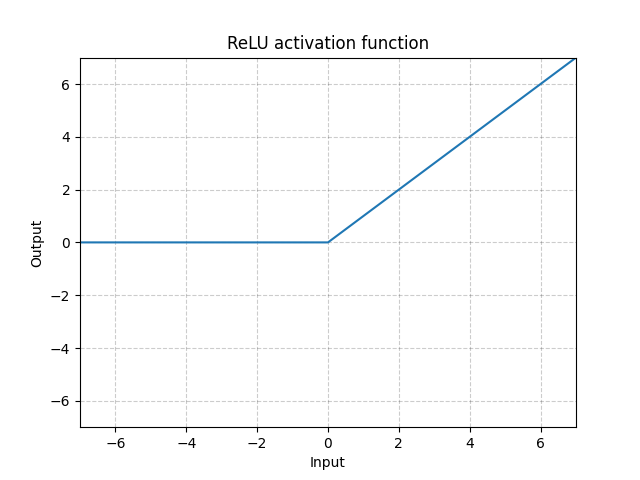
Figure 1 : ReLU

RReLU - nn.RReLU()

Il y a des variations de la ReLU. La ReLU aléatoire (RReLU pour Random ReLU) est définie comme suit :

\[\text{RReLU}(x) = \begin{cases} x, & \text{si } x \geq 0\\ ax, & \text{sinon} \end{cases}\]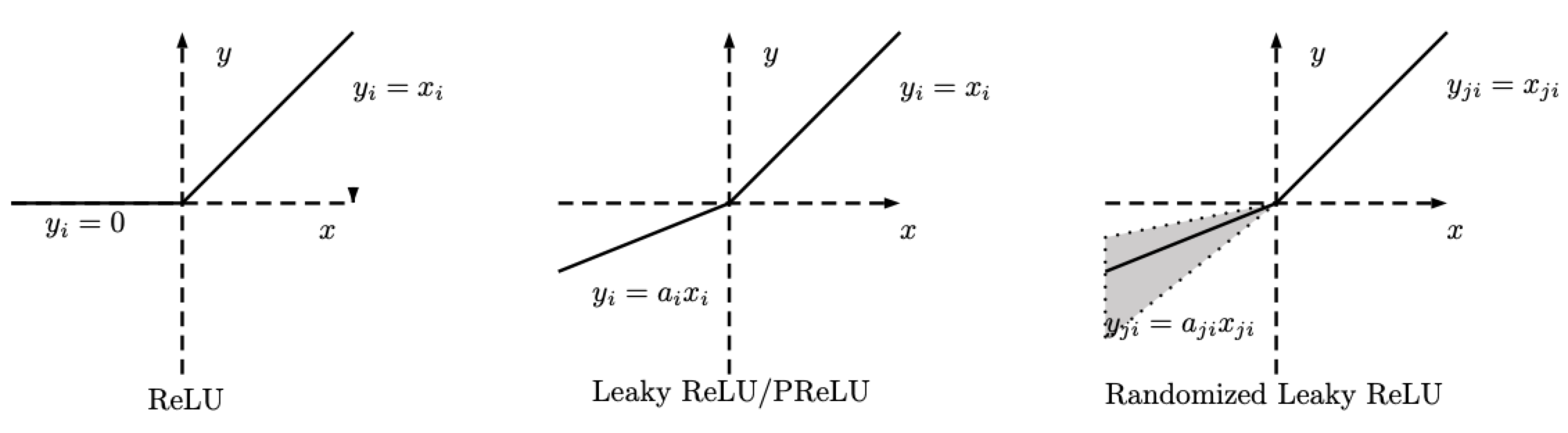
Figure 2 : ReLU, Leaky ReLU/PReLU, RReLU

Notez que pour la RReLU, $a$ est une variable aléatoire qui maintient les échantillonages dans une fourchette donnée pendant l’entraînement, et reste fixe pendant le test. Pour la PReLU, $a$ est également appris. Pour la LeakyReLU, $a$ est fixe.

LeakyReLU - nn.LeakyReLU()

\[\text{LeakyReLU}(x) = \begin{cases} x, & \text{si } x \geq 0\\ a_\text{negative slope}x, & \text{sinon} \end{cases}\]
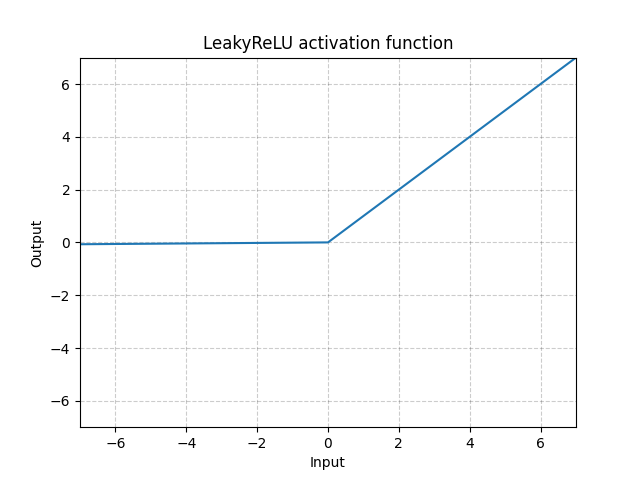
Figure 3 : LeakyReLU

Ici, $a$ est un paramètre fixe. La partie inférieure de l’équation évite que les neurones ReLU deviennent inactifs et ne renvoient à chaque fois 0 pour toute entrée donnée. Par conséquent, sa pente est nulle. En utilisant une pente négative, la fonction permet au réseau de se rétropropager et d’apprendre quelque chose d’utile.

Avec la LeakyReLU, le réseau peut toujours avoir des gradients même si nous sommes dans une région où tout est à zéro.

PReLU - nn.PReLU()

\[\text{PReLU}(x) = \begin{cases} x, & \text{si } x \geq 0\\ ax, & \text{sinon} \end{cases}\]

Ici, $a$ est un paramètre qui peut être appris.

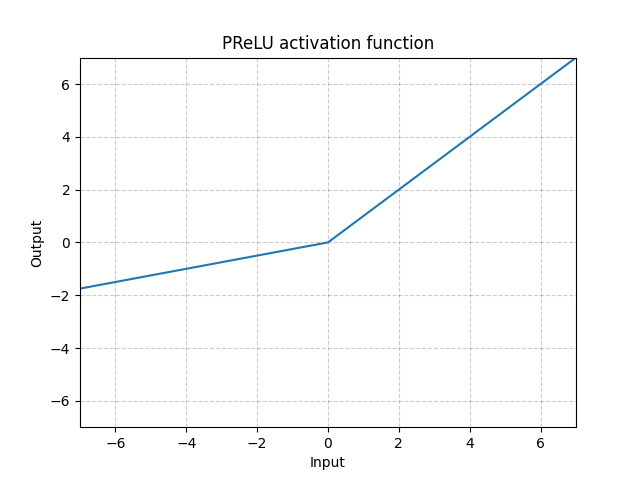
Figure 4 : PReLU

Les fonctions d’activation ci-dessus (ReLU, LeakyReLU, PReLU) sont invariantes au changement d’échelle.

Softplus - Softplus()

\[\text{Softplus}(x) = \frac{1}{\beta} * \log(1 + \exp(\beta * x))\]
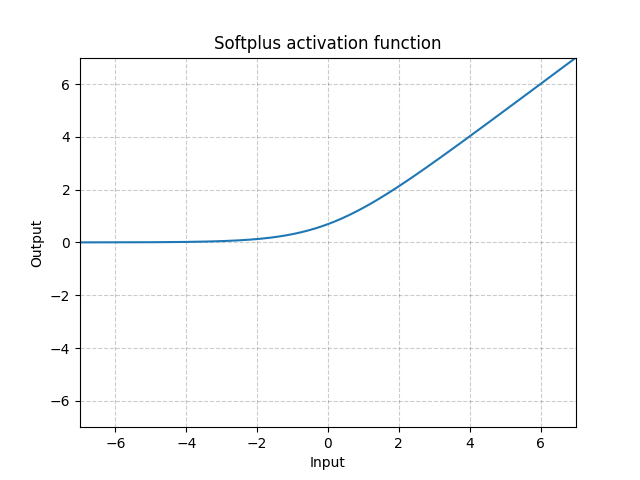
Figure 5 : Softplus

La softplus est une approximation lisse de la fonction ReLU et peut être utilisée pour contraindre la sortie d’une machine à toujours être positive.

La fonction ressemble davantage à la fonction ReLU quand le $\beta$ augmente.

ELU - nn.ELU()

\[\text{ELU}(x) = \max(0, x) + \min(0, \alpha * (\exp(x) - 1)\]
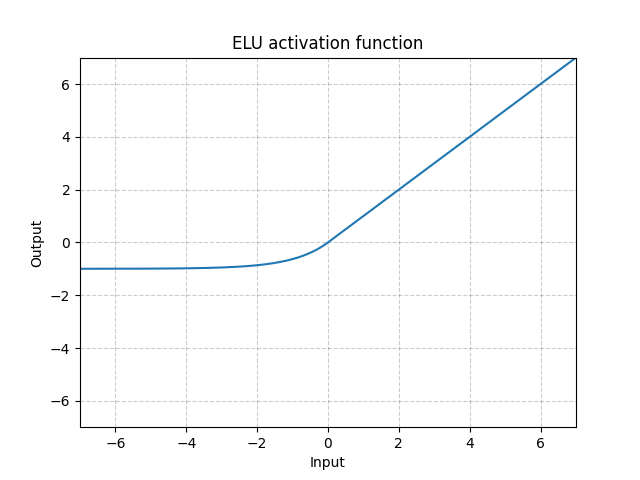
Figure 6 : ELU

Contrairement à la ReLU, cette fonction peut descendre en dessous de 0, ce qui permet au système d’avoir une sortie moyenne de $0$. Par conséquent, le modèle peut converger plus rapidement. Ses variations (CELU, SELU) ne sont que des paramétrages différents.

CELU - nn.CELU()

\[\text{CELU}(x) = \max(0, x) + \min(0, \alpha * (\exp(x/\alpha) - 1)\]
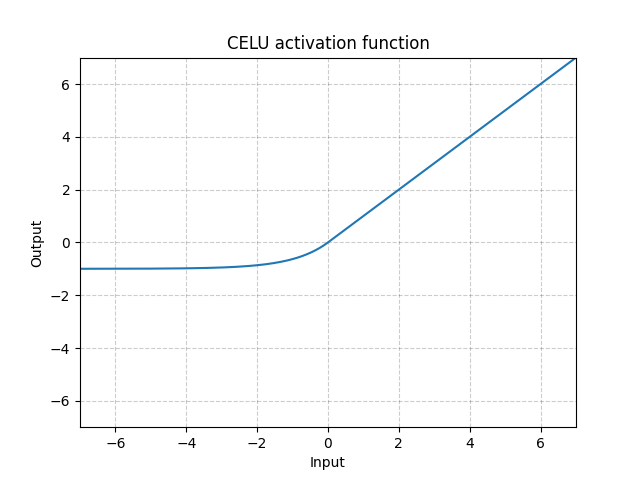
Figure 7 : CELU

SELU - nn.SELU()

\[\text{SELU}(x) = \text{scale} * (\max(0, x) + \min(0, \alpha * (\exp(x) - 1))\]
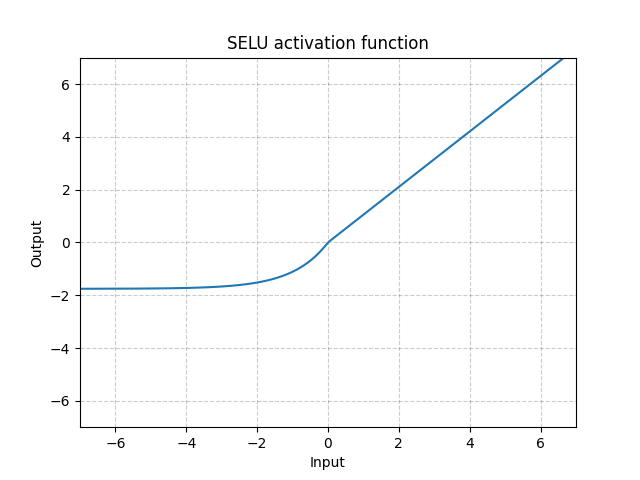
Figure 8 : SELU

GELU - nn.GELU()

\[\text{GELU(x)} = x * \Phi(x)\]

où $\Phi(x)$ est la fonction de distribution cumulative pour la distribution gaussienne.

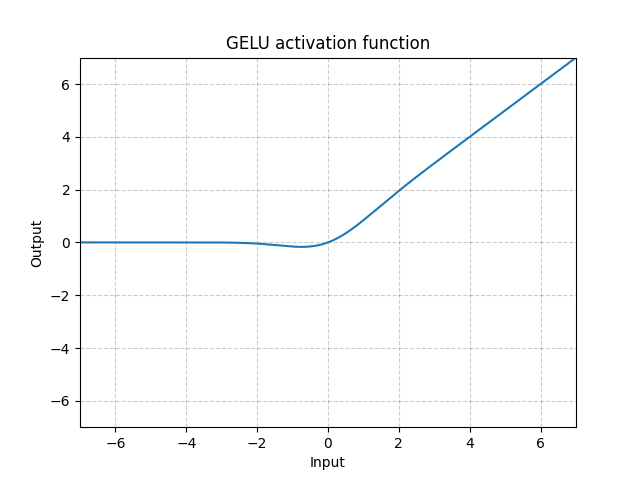
Figure 9 : GELU

ReLU6 - nn.ReLU6()

\[\text{ReLU6}(x) = \min(\max(0,x),6)\]
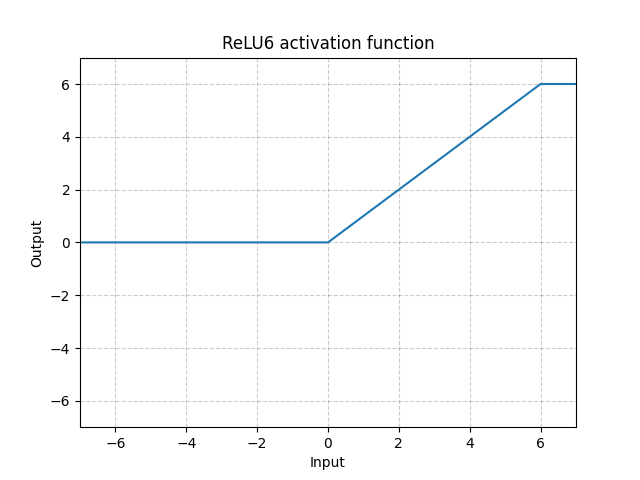
Figure 10 : ReLU6

C’est la saturation de la ReLU à 6. Mais il n’y a pas de raison particulière de choisir 6 comme saturation, nous pouvons donc faire mieux en utilisant la fonction Sigmoïde ci-dessous.

Sigmoïde - nn.Sigmoid()

\[\text{Sigmoid}(x) = \sigma(x) = \frac{1}{1 + \exp(-x)}\]
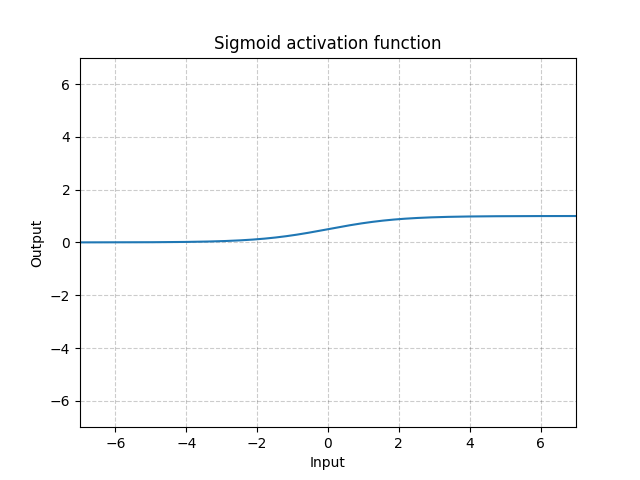
Figure 11 : Sigmoïde

Si nous empilons des sigmoïdes sur plusieurs couches, cela peut être inefficace pour l’apprentissage et nécessite une initialisation soigneuse. En effet, si l’entrée est très grande ou très petite, le gradient de la fonction sigmoïde est proche de 0. Dans ce cas, il n’y a pas de retour de gradient pour mettre à jour les paramètres. C’est ce qu’on appelle le problème de la saturation du gradient. C’est pourquoi, pour les réseaux neuronaux profonds, une seule fonction (comme la ReLU) est préférable.

Tanh - nn.Tanh()

\[\text{Tanh}(x) = \tanh(x) = \frac{\exp(x) - \exp(-x)}{\exp(x) + \exp(-x)}\]
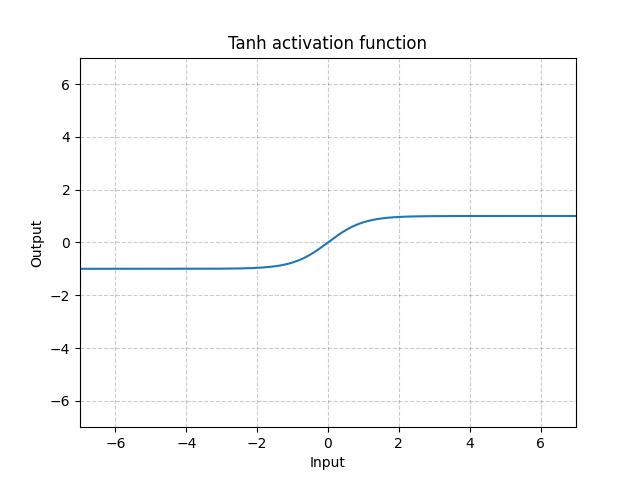
Figure 12 : Tanh

Tanh est fondamentalement identique à la Sigmoïde sauf qu’elle est centrée et va de $-1$ à $1$. La sortie de la fonction a une moyenne à peu près nulle. Par conséquent, le modèle converge plus rapidement. A noter que la convergence est généralement plus rapide si la moyenne de chaque variable d’entrée est proche de $0$. Un exemple est la normalisation par batch.

Softsign - nn.Softsign()

\[\text{SoftSign}(x) = \frac{x}{1 + |x|}\]
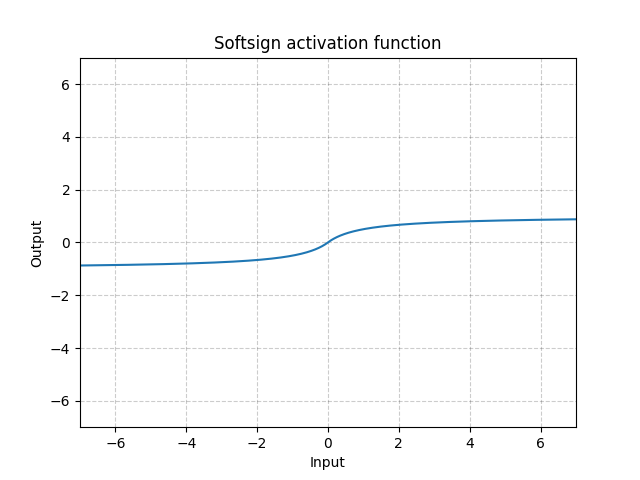
Figure 13 : Softsign

Elle est similaire à la fonction Sigmoïde mais arrive lentement à l’asymptote et atténue le problème de la disparition du gradient (dans une certaine mesure).

Hardtanh - nn.Hardtanh()

\[\text{HardTanh}(x) = \begin{cases} 1, & \text{si } x > 1\\ -1, & \text{si } x < -1\\ x, & \text{sinon} \end{cases}\]

L’étendue de la région linéaire [$-1$, $1$] peut être ajustée en utilisant min_val et max_val.

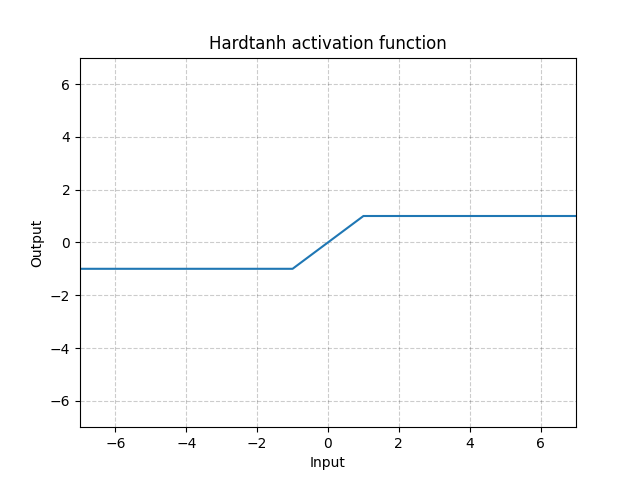
Figure 14 : Hardtanh

Elle fonctionne étonnamment bien, surtout lorsque les poids sont maintenus dans une fourchette de petites valeurs.

Threshold - nn.Threshold()

\[y = \begin{cases} x, & \text{si} x > \text{threshold}\\ v, & \text{sinon} \end{cases}\]

Rarement utilisée car nous ne pouvons pas rétropropager le gradient. C’est aussi la raison pour laquelle les gens ne pouvaient pas utiliser la rétropropagation dans les années 60 et 70 lorsqu’ils utilisaient des neurones binaires.

Tanhshrink - nn.Tanhshrink()

\[\text{Tanhshrink}(x) = x - \tanh(x)\]
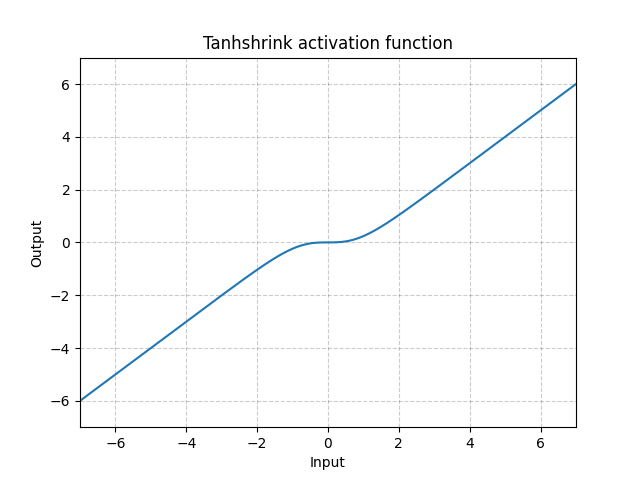
Figure 15 : Tanhshrink

Elle est rarement utilisée sauf pour les codages épars afin de calculer la valeur de la variable latente.

Softshrink - nn.Softshrink()

\[\text{SoftShrinkage}(x) = \begin{cases} x - \lambda, & \text{si } x > \lambda\\ x + \lambda, & \text{si } x < -\lambda\\ 0, & \text{sinon} \end{cases}\]
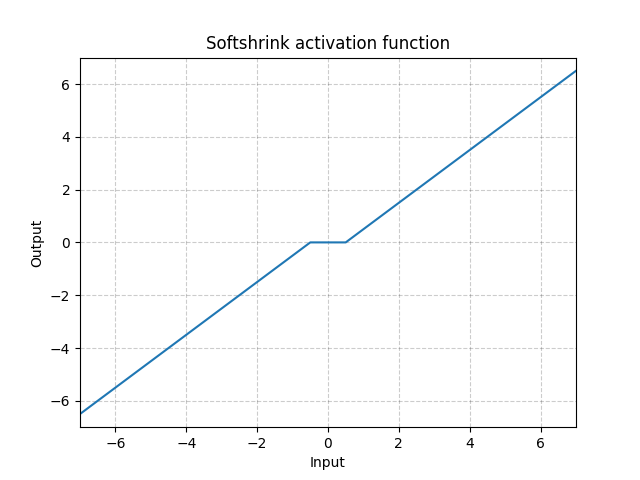
Figure 16 : Softshrink

Grossièrement, cela réduit la variable d’une constante vers $0$ et la force à $0$ si la variable est proche de $0$. Elle peut être considérée comme une étape de gradient pour le critère $\ell_1$. C’est également l’une des étapes de l’algorithme ISTA (Iterative Shrinkage-Thresholding Algorithm). Mais elle n’est pas couramment utilisée comme activation dans les réseaux de neurones standard.

Hardshrink - nn.Hardshrink()

\[\text{HardShrinkage}(x) = \begin{cases} x, & \text{si } x > \lambda\\ x, & \text{si } x < -\lambda\\ 0, & \text{sinon} \end{cases}\]
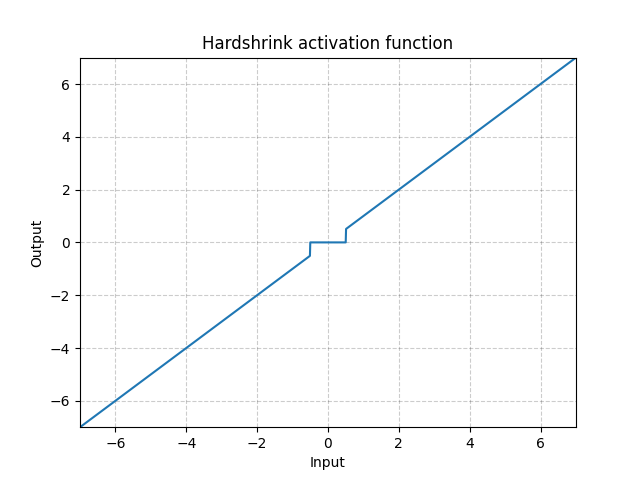
Figure 17 : Hardshrink

Rarement utilisée sauf pour des codages épars.

LogSigmoid - nn.LogSigmoid()

\[\text{LogSigmoid}(x) = \log\left(\frac{1}{1 + \exp(-x)}\right)\]
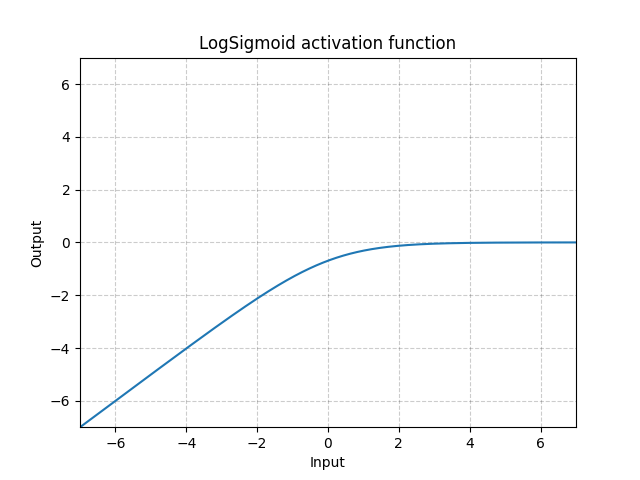
Figure 18 : LogSigmoid

Principalement utilisée comme fonction de perte mais n’est pas couramment comme fonction d’activation.

Softmin - nn.Softmin()

\[\text{Softmin}(x_i) = \frac{\exp(-x_i)}{\sum_j \exp(-x_j)}\]

Transforme les chiffres en une distribution de probabilité.

Soft(arg)max - nn.Softmax()

\[\text{Softmax}(x_i) = \frac{\exp(x_i)}{\sum_j \exp(x_j)}\]

LogSoft(arg)max - nn.LogSoftmax()

\[\text{LogSoftmax}(x_i) = \log\left(\frac{\exp(x_i)}{\sum_j \exp(x_j)}\right)\]

Principalement utilisée comme fonction de perte mais n’est pas couramment comme fonction d’activation.

Questions des étudiants sur les fonctions d’activation

Questions relatives à nn.PRELU()

Pourquoi voudrait-on la même valeur de $a$ pour toutes les canaux ?

Différents canaux pourraient avoir des $a$ différents. Vous pourriez utiliser $a$ comme paramètre de chaque unité. Il pourrait également être partagé sous forme de carte de caractéristiques.

Est-ce qu’on apprend $a$ ? Est-il avantageux d’apprendre $a$ ?

Vous pouvez apprendre $a$ ou le corriger. La raison de la correction est de s’assurer que la non-linéarité vous donne un gradient non nul même s’il est dans une région négative. Rendre $a$ apprenable permet au système de transformer la non-linéarité en une association linéaire ou une rectification complète. Cela peut être utile pour certaines applications comme la mise en œuvre d’un détecteur de bord, quelle que soit la polarité du bord.

Quelle complexité souhaitez-vous donner à la non-linéarité ?

Théoriquement, nous pouvons paramétrer une fonction non linéaire entière de manière très compliquée, comme avec des paramètres de ressort, le polynôme de Tchebyshev, etc. Le paramétrage pourrait faire partie du processus d’apprentissage.

Quel est l’avantage du paramétrage par rapport au fait d’avoir plus d’unités dans le système ?

Cela dépend vraiment de ce que vous voulez faire. Par exemple, lorsque vous faites une régression dans un espace de faible dimension, le paramétrage peut vous aider. Cependant, si votre tâche se situe dans un espace à haute dimension comme la reconnaissance d’images, une simple non-linéarité « a » est nécessaire et une non-linéarité monotone fonctionnera mieux. En bref, vous pouvez paramétrer toutes les fonctions que vous voulez, mais cela n’apporte pas un énorme avantage.

Questions relatives aux coudes

Un coude contre un double coude

Le double coude a une échelle intégrée. Cela signifie que si la couche d’entrée est multipliée par deux (ou si l’amplitude du signal est multipliée par deux), les sorties seront complètement différentes. Le signal sera plus en non-linéarité, donc vous obtiendrez un comportement complètement différent de la sortie. Alors que si vous avez une fonction avec un seul coude, si vous multipliez l’entrée par deux, alors votre sortie sera également multipliée par deux.

Différences entre une activation non linéaire ayant des coudes et une activation non linéaire lisse. Pourquoi/quand l’une d’entre elles est préférée ?

C’est une question d’équivariance d’échelle. Si le coude est difficile, vous multipliez l’entrée par deux et la sortie est multipliée par deux. Si vous avez une transition en douceur, par exemple si vous multipliez l’entrée par $100$, la sortie semble avoir un coude dur parce que la partie lisse est réduite d’un facteur $100$. Si vous divisez l’entrée par $100$, le coude devient une fonction convexe très lisse. Ainsi, en changeant l’échelle de l’entrée, vous modifiez le comportement de l’unité d’activation. Parfois, cela peut poser un problème. Par exemple, lorsque vous entraînez un réseau neuronal multicouche et que vous avez deux couches qui se suivent l’une l’autre. Vous n’avez pas un bon contrôle sur la taille des poids d’une couche par rapport aux poids de l’autre couche. Si vous avez une non-linéarité qui se soucie des échelles, votre réseau n’a pas le choix de la taille de la matrice de poids qui peut être utilisée dans la première couche car cela changera complètement le comportement. Une façon de résoudre ce problème est de fixer une échelle dure sur les poids de chaque couche afin de pouvoir normaliser les poids des couches, comme la batch normalisation. Ainsi, la variance qui va dans une unité devient toujours constante. Si vous fixez l’échelle, alors le système n’a aucun moyen de choisir quelle partie de la non-linéarité sera utilisée dans deux systèmes de fonction de coude. Cela peut poser un problème si cette partie fixe devient trop linéaire. Par exemple, Sigmoïde devient presque linéaire près de $0$ et donc les sorties de la batch normalisation (proches de $0$) ne pourraient pas être activées non linéairement. Il n’est pas tout à fait clair pourquoi les réseaux profonds fonctionnent mieux avec des fonctions de coude unique. C’est probablement dû à la propriété d’équivariance d’échelle.

Coefficient de température dans une fonction soft(arg)max

Quand utilisons-nous le coefficient de température et pourquoi l’utilisons-nous ?

Dans une certaine mesure, la température est redondante avec les poids entrants. Si vous avez des sommes pondérées qui arrivent dans votre softmax, le paramètre $\beta$ est redondant avec la taille des poids. La température contrôle le degré de difficulté de la distribution des sorties. Lorsque $\beta$ est très grand, il devient très proche de $1$ ou de $0$. Lorsque $\beta$ est petit, il est plus doux. Lorsque la limite de $\beta$ est égale à $0$, c’est comme une moyenne. Lorsque $\beta$ va à l’infini, il se comporte comme argmax. Ce n’est plus sa version douce. Ainsi, si vous avez une sorte de normalisation avant le softmax, alors, le réglage de ce paramètre vous permet de contrôler la dureté. Parfois, vous pouvez commencer avec un petit $\beta$ afin d’avoir des descentes de gradient bien conduites et ensuite, au fur et à mesure que la course avance, si vous voulez une décision plus difficile dans votre mécanisme d’attention, vous augmentez $\beta$. Ainsi, vous pouvez affiner les décisions. Il peut être utile pour un mélange d’experts comme un mécanisme d’auto-attention.

Fonctions de perte

PyTorch a également mis en place de nombreuses fonctions de perte. Nous allons en passer quelques-unes en revue ici.

nn.MSELoss()

Cette fonction donne l’erreur quadratique moyenne (norme L2 au carré) entre chaque élément de l’entrée $x$ et la cible $y$. Elle est également appelée perte L2.

Si nous utilisons un mini-lot d’échantillons $n$, alors il y a des pertes $n$, une pour chaque échantillon du lot. Nous pouvons dire à la fonction de perte de conserver cette perte comme vecteur ou de la réduire.

Si elle n’est pas réduite (reduction='none'), la perte est :

\[l(x,y) = L = \{l_1, \dots, l_N\}^\top, l_n = (x_n - y_n)^2\]

où $N$ est la taille du lot, $x$ et $y$ sont des tenseurs de formes arbitraires avec un total de n éléments chacun.

Les options de réduction sont ci-dessous (notez que la valeur par défaut est reduction='mean').

\[l(x,y) = \begin{cases}\text{mean}(L), \quad &\text{si reduction='mean'}\\ \text{sum}(L), \quad &\text{si reduction='sum'} \end{cases}\]

L’opération de la somme fonctionne toujours sur tous les éléments et se divise par $n$.

La division par $n$ peut être évitée si l’on définit reduction = 'sum'.

nn.L1Loss()

Elle mesure l’erreur moyenne absolue entre chaque élément de l’entrée $x$ et de la cible $y$ (ou entre la sortie réelle et la sortie souhaitée).

Si elle n’est pas réduite (reduction='none'), la perte est

\[l(x,y) = L = \{l_1, \dots, l_N\}^\top, l_n = \vert x_n - y_n\vert\]

où $N$ est la taille du lot, $x$ et $y$ sont des tenseurs de formes arbitraires avec un total de $n$ éléments chacun.

Il dispose également d’une option reduction de 'mean' et 'sum', similaire à celle de nn.MSELoss().

Cas d’utilisation : la perte L1 est plus robuste contre les valeurs aberrantes et le bruit que la perte L2. En L2, les erreurs de ces points aberrants/bruits sont élevées au carré, de sorte que la fonction de coût devient très sensible aux aberrants.

Problème : la perte en L1 n’est pas différentiable dans la partie inférieure (0). Nous devons être prudents lorsque nous traitons ses gradients (à savoir la Softshrink). C’est ce qui motive la perte L1 lisse suivante.

nn.SmoothL1Loss()

Cette fonction utilise la perte de L2 si l’erreur absolue au niveau de l’élément tombe en dessous de $1$ et la perte de L1 dans le cas contraire.

\(\text{loss}(x, y) = \frac{1}{n} \sum_i z_i\) où $z_i$ est donné par

\[z_i = \begin{cases}0.5(x_i-y_i)^2, \quad &\text{si } |x_i - y_i| < 1\\\\ |x_i - y_i| - 0,5, \quad &\text{sinon} \end{cases}\]

Elle dispose également d’options de reduction.

Elle est utilisée par Ross Girshick dans Fast R-CNN. La perte L1 lisse est également connue sous le nom de perte de Huber ou d’ElasticNet lorsqu’elle est utilisée comme fonction objective.

Cas d’utilisation : elle est moins sensible aux valeurs aberrantes que la MSELoss et est lisse dans le bas. Cette fonction est souvent utilisée en vision par ordinateur pour se protéger contre les valeurs aberrantes.

Problème : cette fonction a une échelle ($0,5$ dans la fonction ci-dessus).

L1 vs L2 pour la vision par ordinateur

En faisant des prédictions quand nous avons beaucoup de $y$ différents :

• Si nous utilisons la MSE (perte L2), nous obtenons une moyenne de tous les $y$, ce qui signifie que nous aurons une image floue.
• Si nous utilisons la perte L1, la valeur $y$ qui minimise la distance L1 est le milieu, qui n’est pas flou, mais notons que le milieu est difficile à définir en plusieurs dimensions.

L’utilisation de la distance L1 donne une image plus nette pour la prédiction.

nn.NLLLoss()

Il s’agit de la perte de probabilité logarithmique négative utilisée lors de l’entraînement d’un problème de classification à $C$ classes.

Mmathématiquement, l’entrée de NLLLoss devrait être la probabilité (log), mais PyTorch ne l’impose pas. L’effet est donc de rendre la composante désirée aussi grande que possible.

La perte non réduite (avec :attr:reduction réglé sur 'none') peut être décrite comme :

\[\ell(x, y) = L = \{l_1,\dots,l_N\}^\top, \quad l_n = - w_{y_n} x_{n,y_n}, \quad w_{c} = \text{weight}[c] \cdot \mathbb{1}\{c \not= \text{ignore\_index}\}\]

où $N$ est la taille du lot.

Si reduction n’est pas à 'none' (par défaut 'mean'), alors :

\[\ell(x, y) = \begin{cases} \sum_{n=1}^N \frac{1}{\sum_{n=1}^N w_{y_n}} l_n, & \text{si reduction} = \text{"mean";}\\\\ \sum_{n=1}^N l_n, & \text{si reduction} = \text{"sum".} \end{cases}\]

Cette fonction de perte a un argument optionnel weight qui peut être transmis en utilisant un tenseur 1D qui assigne un poids à chacune des classes. Ceci est utile lorsqu’il s’agit d’un jeu d’entraînement déséquilibré.

Poids et classes déséquilibrées :

Le vecteur de poids est utile si la fréquence est différente pour chaque catégorie/classe. Par exemple, la fréquence de la grippe commune est beaucoup plus élevée que celle du cancer du poumon. Nous pouvons simplement augmenter le poids pour les catégories qui ont un petit nombre d’échantillons.

Cependant, au lieu de fixer le poids, il est préférable d’égaliser la fréquence à l’entraînement afin de mieux exploiter les gradients stochastiques.

Pour égaliser les classes à l’entraînement, nous plaçons des échantillons de chaque classe dans une mémoire tampon différente. Ensuite, nous générons chaque mini-batch en prélevant le même nombre d’échantillons dans chaque tampon. Lorsque le petit tampon est à court d’échantillons à utiliser, nous itérons à nouveau à travers le petit tampon depuis le début jusqu’à ce que chaque échantillon de la grande classe soit utilisé. De cette façon, nous obtenons une fréquence égale pour toutes les catégories en passant par ces tampons. Nous ne devrions jamais utiliser la méthode facile pour égaliser la fréquence en n’ utilisant pas tous les échantillons de la classe majoritaire. Ne laissez pas de données de côté !

Un problème évident de la méthode ci-dessus est que notre modèle ne connaîtrait pas la fréquence relative des échantillons réels. Pour résoudre ce problème, nous affinons le système en exécutant quelques époques à la fin avec la fréquence réelle de la classe, de sorte que le système s’adapte aux biais de la couche de sortie pour favoriser les choses qui sont plus fréquentes.

Pour avoir une intuition de ce schéma, revenons à l’exemple de la faculté de médecine : les étudiants passent autant de temps sur les maladies rares que sur les maladies fréquentes (ou peut-être même plus de temps, puisque les maladies rares sont souvent les plus complexes). Ils apprennent à s’adapter aux caractéristiques de chacune d’entre elles, puis à les corriger pour savoir lesquelles sont rares.

nn.CrossEntropyLoss()

Cette fonction combine nn.LogSoftmax et nn.NLLLoss dans une seule classe. La combinaison des deux rend le score de la classe correcte aussi grand que possible.

La raison pour laquelle les deux fonctions sont fusionnées ici est la stabilité numérique du calcul du gradient. Lorsque la valeur après softmax est proche de $1$ ou $0$, le log de cette fonction peut se rapprocher de $0$ ou $-\infty$. La pente du log proche de $0$ est proche de $-\infty$, ce qui entraîne des problèmes numériques à l’étape intermédiaire de la rétropropagation. Lorsque les deux fonctions sont combinées, le gradient est saturé, de sorte que nous obtenons un nombre raisonnable à la fin.

On s’attend à ce que l’entrée soit un score non normalisé pour chaque classe.

La perte peut être décrite comme suit :

\[\text{loss}(x, c) = -\log\left(\frac{\exp(x[c])}{\sum_j \exp(x[j])}\right) = -x[c] + \log\left(\sum_j \exp(x[j])\right)\]

ou dans le cas où l’argument weight est spécifié :

\[\text{loss}(x, c) = w[c] \left(-x[c] + \log\left(\sum_j\exp(x[j])\right)\right)\]

La moyenne des pertes est calculée à partir des observations de chaque mini-batch.

Une interprétation physique de la perte d’entropie croisée est liée à la divergence de Kullback-Leibler (divergence KL), où nous mesurons la divergence entre deux distributions. Ici, les (quasi) distributions sont représentées par le vecteur $x$ (prédictions) et la distribution cible (un vecteur one-hot avec $0$ sur les mauvaises classes et $1$ sur la bonne classe).

Mathématiquement :

\[H(p,q) = H(p) + \mathcal{D}_{KL} (p \mid\mid q)\]

où \(H(p,q) = - \sum_i p(x_i) \log (q(x_i))\) est l’entropie croisée (entre deux distributions), \(H(p) = - \sum_i p(x_i) \log (p(x_i))\) est l’entropie, et \(\mathcal{D}_{KL} (p \mid\mid q) = \sum_i p(x_i) \log \frac{p(x_i)}{q(x_i)}\) est la divergence KL.

nn.AdaptiveLogSoftmaxWithLoss()

Il s’agit d’une approximation efficace de la softmax pour un grand nombre de classes (par exemple, des millions de classes). Elle met en œuvre des astuces pour améliorer la rapidité du calcul. Les détails de la méthode sont décrits dans Efficient softmax approximation for GPUs de Grave et al.

---

📝 Haochen Wang, Eunkyung An, Ying Jin, Ningyuan Huang
Loïck Bourdois
13 April 2020