Fonctions de perte (continues) et fonctions de perte pour les EBMs

Perte d’entropie croisée binaire (Binary Cross Entropy : BCE) - nn.BCELoss()

Cette perte est un cas particulier de l’entropie croisée car lorsque nous n’avons que deux classes, elle peut être réduite à une fonction plus simple. Elle est utilisée pour mesurer l’erreur d’une reconstruction dans, par exemple un auto-encodeur. Cette formule suppose que $x$ et $y$ sont des probabilités, elles sont donc strictement comprises entre $0$ et $1$.

Perte de divergence de Kullback-Leibler - nn.KLDivLoss()

Il s’agit d’une fonction de perte simple pour les cas où la cible est une distribution one-hot (c’est-à-dire que $y$ est une catégorie). Là encore, elle suppose que $x$ et $y$ sont des probabilités. Elle présente l’inconvénient de ne pas être fusionnée avec une softmax ou une log-softmax, ce qui peut poser des problèmes de stabilité numérique.

BCE Loss with Logits - nn.BCEWithLogitsLoss()

Cette version de la perte d’entropie croisée binaire prend les scores qui ne sont pas passés par la softmax, donc elle ne suppose pas que $x$ est compris entre $0$ et $1$. Elle passe ensuite par une sigmoïde pour s’assurer qu’elle est dans cette fourchette. La fonction de perte a plus de chances d’être numériquement stable lorsqu’elle est combinée de cette manière.

Perte Margin Ranking - nn.MarginRankingLoss()

Les pertes avec marge constituent une catégorie importante de pertes. Si nous avons deux entrées, cette fonction de perte indique que l’une d’elles doit être plus importante que l’autre d’au moins une marge. Dans ce cas, $y$ est une variable binaire $\in { -1, 1}$. Imaginons que les deux entrées sont des scores de deux catégories. Nous voulons que le score de la catégorie correcte soit plus grand que le score de la catégorie incorrecte d’au moins une certaine marge. Comme pour la perte Hinge, si $y*(x_1-x_2)$ est supérieur à la marge, le coût est de $0$. S’il est inférieur, le coût augmente de façon linéaire. Si nous devons l’utiliser pour la classification, nous aurions $x_1$ comme score de la bonne réponse et $x_2$ comme score de la réponse incorrecte la plus élevée du mini-batch. Si elle est utilisée dans des modèles à base d’énergie (voir plus loin), cette fonction de perte pousse vers le bas la bonne réponse $x_1$ et vers le haut la mauvaise réponse $x_2$.

Perte Triplet Margin - nn.TripletMarginLoss()

Cette perte est utilisée pour mesurer une similarité relative entre les échantillons. Par exemple, nous faisons passer deux images de même catégorie dans un ConvNet et nous obtenons deux vecteurs. Nous voulons que la distance entre ces deux vecteurs soit la plus petite possible. Cette fonction de perte essaie d’envoyer la première distance vers $0$ et la seconde distance plus grande qu’une certaine marge. Cependant, la seule chose qui importe est que la distance entre la bonne paire soit plus petite que la distance entre la mauvaise paire.

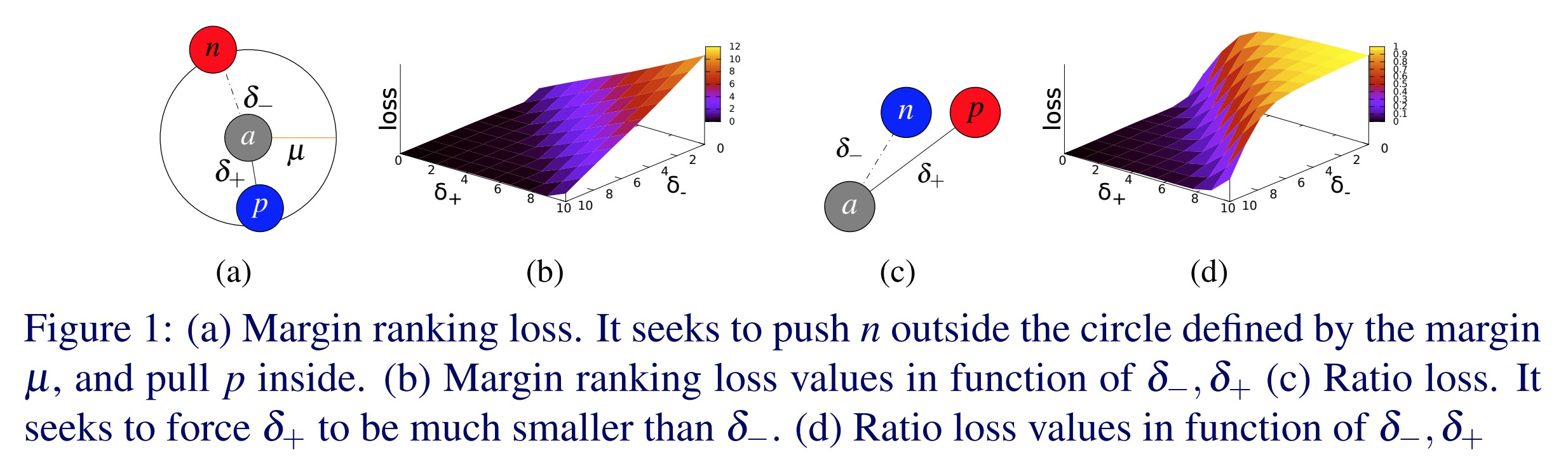
Figure 1 : Perte Triplet Margin

Elle a été utilisée à l’origine pour l’entraînement d’un système de recherche d’images pour Google. À l’époque, il fallait taper une requête dans Google et celui-ci l’encodait dans un vecteur. Il comparait ensuite ce vecteur à un ensemble de vecteurs provenant d’images qui avaient été précédemment indexées. Google récupère alors les images qui sont les plus proches de votre vecteur.

Perte SoftMargin - nn.SoftMarginLoss()

Crée un critère qui optimise une perte logistique de classification à deux classes entre le tenseur d’entrée $x$ et le tenseur cible $y$ (contenant $1$ ou $-1$).

• C’est la version softmax de la perte avec marge. Nous avons un tas de positifs et un tas de négatifs que nous voulons faire passer par une softmax. Cette fonction de perte tente alors de rendre $\text{exp}(-y[i]*x[i])$ plus petit que les autres pour le bon $x[i]$.
• Cette fonction de perte veut rapprocher les valeurs positives de $y[i]*x[i]$ et éloigner les valeurs négatives, mais par opposition à une marge fixe, avec un effet continu de décroissance exponentielle sur la perte.

Perte Multi-Class Hinge - nn.MultiLabelMarginLoss()

Cette perte permet à différentes entrées d’avoir des quantités variables d’objectifs. Dans ce cas, nous avons plusieurs catégories pour lesquelles nous souhaitons obtenir des scores élevés et elle additionne la perte sur toutes les catégories. Pour les EBMs, cette fonction de perte pousse vers le bas les catégories souhaitées et vers le haut les catégories non souhaitées.

Perte Hinge Embedding - nn.HingeEmbeddingLoss()

Cette perte est utilisée pour l’apprentissage semisupervisé en mesurant si deux entrées sont similaires ou dissemblables. Elle rassemble les choses qui sont similaires et repousse celles qui sont dissemblables. La variable $y$ indique si la paire de notes doit aller dans une certaine direction. En utilisant une telle perte, le score est positif si $y$ est égal à $1$ et une certaine marge $\Delta$ si $y$ est égal à $-1$.

Perte Cosine Embedding - nn.CosineEmbeddingLoss()

Cette perte est utilisée pour mesurer si deux entrées sont similaires ou dissemblables, en utilisant la distance cosinusoïdale et est généralement utilisée pour l’apprentissage d’enchâssements non linéaires ou pour l’apprentissage semisupervisé.

• Pensée d’une autre manière, $1$ moins le cosinus de l’angle entre les deux vecteurs est fondamentalement la distance euclidienne normalisée.
• L’avantage de cette méthode est que lorsque nous avons deux vecteurs et que voulons rendre leur distance aussi grande que possible, il est très facile de faire en sorte que le réseau y parvienne en rendant les vecteurs très longs. Bien sûr, ce n’est pas optimal. Nous ne voulons pas que le système fabrique des vecteurs de grande taille, mais qu’il fasse tourner les vecteurs dans la bonne direction, de sorte que nous normalisons les vecteurs et calculons la distance euclidienne normalisée.
• Pour les cas positifs, cette perte essaie de rendre les vecteurs aussi alignés que possible. Pour les paires négatives, cette perte essaie de rendre le cosinus plus petit qu’une marge particulière. La marge doit ici être une petite valeur positive.
• Dans un espace de grande dimension, il y a beaucoup de régions près de l’équateur de la sphère. Après la normalisation, tous nos points sont maintenant normalisés sur la sphère. Ce que nous voulons, c’est que les échantillons qui nous ressemblent sémantiquement soient proches. Les échantillons qui sont dissemblables doivent être orthogonaux. Nous ne voulons pas qu’ils soient opposés entre eux car il n’y a qu’un seul point au pôle opposé. Au contraire, sur l’équateur, il y a une très grande quantité d’espace, donc nous voulons que la marge ait une petite valeur positive afin de pouvoir profiter de toute cette zone.

La perte Connectionist Temporal Classification (CTC) - nn.CTCLoss()

Calcule la perte entre une série chronologique continue (non segmentée) et une séquence cible.

• Les sommes des pertes CTC sur la probabilité des alignements possibles de l’entrée vers la cible, produisent une valeur de perte qui est différenciable par rapport à chaque nœud d’entrée.
• L’alignement de l’entrée sur la cible est supposé être « plusieurs vers un », ce qui limite la longueur de la séquence cible de sorte qu’elle doit être inférieure ou égale à la longueur d’entrée.
• Utile lorsque votre sortie est une séquence de vecteurs, qui correspond à un grand nombre de catégories.

Figure 2 : Perte CTC pour la reconnaissance vocale

Exemple d’un système de reconnaissance vocale :

• Objectif : prédire quel mot est prononcé toutes les 10 millisecondes.
• Chaque mot est représenté par une séquence de sons.
• En fonction de la vitesse de la personne qui parle, des sons de différentes longueurs peuvent être associés au même mot.
• Trouver la meilleure correspondance entre la séquence d’entrée et la séquence de sortie. Une bonne méthode pour cela consiste à utiliser la programmation dynamique pour trouver le chemin le moins coûteux.

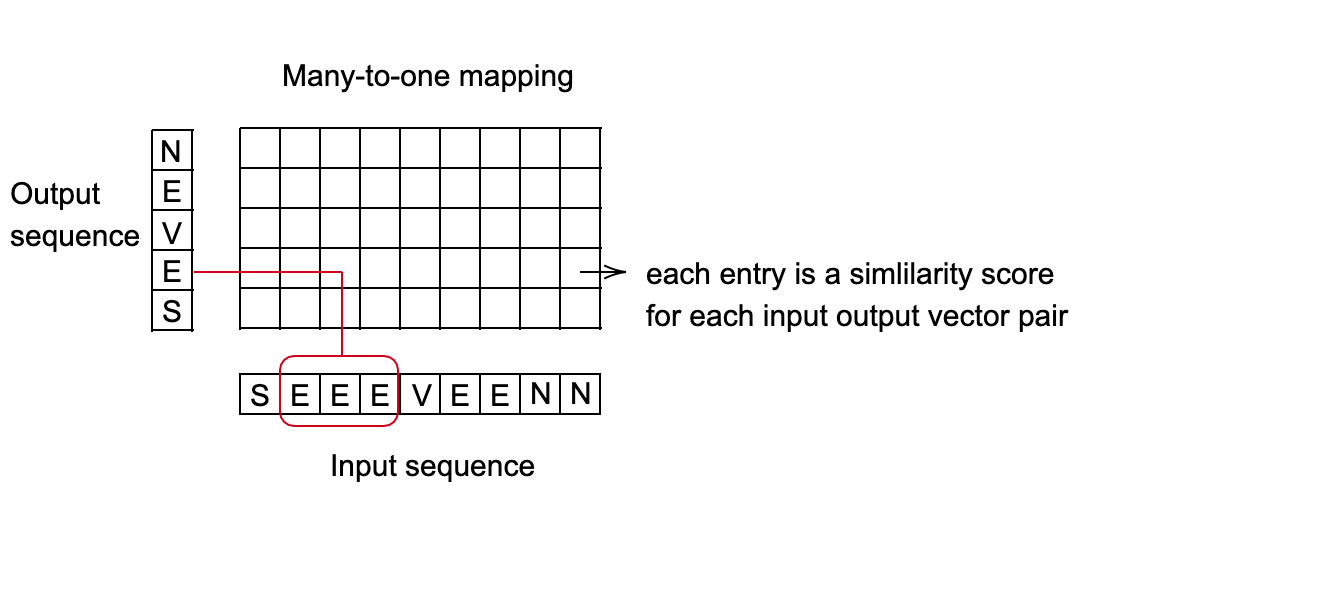
Figure 3 : Configuration « plusieurs vers un »

Modèles à base d’énergie (EBMs) - Fonction de perte

Architecture et perte fonctionnelle

Famille de fonction d’énergie : $\mathcal{E} = {E(W,Y, X) : W \in \mathcal{W}}$.

Jeu d’entraînement : $S = {(X^i, Y^i) : i = 1 \cdots P}$.

Perte fonctionnelle : $\mathcal{L} (E, S)$

• Fonctionnelle signifie une fonction d’une autre fonction. Dans notre cas, la fonction $\mathcal{L} (E, S)$ est une fonction de la fonction d’énergie $E$.
• Comme $E$ est paramétré par $W$, nous pouvons transformer la fonction en une fonction de perte de $W$ : $\mathcal{L} (W, S)$
• Mesure la qualité d’une fonction énergie sur un jeu d’entraînement
• Invariable sous les permutations et les répétitions des échantillons.

Entraînement : $W^* = \arg\min_{W\in \mathcal{W}} \mathcal{L}(W, S)$.

Forme de la perte fonctionnelle :

• $L(Y^i, E(W, \mathcal{Y}, X^i))$ est la perte par échantillon
• $Y^i$ est la réponse souhaitée, peut être une catégorie ou une image entière, etc.
• $E(W, \mathcal{Y}, X^i)$ est la surface d’énergie pour un $X_i$ donné car $Y$ varie
• $R(W)$ est un régulariseur

Concevoir une bonne fonction de perte

Poussez vers le bas sur l’énergie de la bonne réponse.

Poussez vers le haut sur l’énergie des mauvaises réponses, surtout si elles sont plus petites que la bonne réponse.

Exemples de fonctions de perte

Perte d’énergie

Cette fonction de perte pousse simplement vers le bas l’énergie de la bonne réponse. Si le réseau n’est pas conçu correctement, il peut se retrouver avec une fonction de perte d’énergie pratiquement nulle car nous essayons seulement de rendre l’énergie de la bonne réponse faible mais nous ne poussons pas l’énergie vers le haut ailleurs. Ainsi, le système peut s’effondrer.

Perte Negative Log-Likelihood

Cette fonction de perte pousse vers le bas l’énergie de la bonne réponse tout en poussant vers le haut les énergies de toutes les réponses en proportion de leurs probabilités. Cela se réduit à la perte de perceptron lorsque $\beta \rightarrow droite \infty$. Elle est utilisée depuis longtemps pour un entraînement discriminant avec des sorties structurés.

Un modèle probabiliste est un EBM dans lequel :

• L’énergie peut être intégrée sur $Y$ (la variable à prédire)
• La fonction de perte est la log-vraisemblance négative

Perte de perceptron

Très similaire à la perte de perceptron d’il y a plus de 60 ans. Toujours positive car le minimum est également pris en charge $Y^i$, donc $E(W,Y^i,X^i)-\min_{Y\in\mathcal Y} E(W,Y,X^i)\geq E(W,Y^i,X^i)-E(W,Y^i,X^i)=0$. Le même calcul montre qu’il ne donne exactement $0$ que lorsque $Y^i$ est la bonne réponse.

Cette perte rend l’énergie de la bonne réponse faible et en même temps rend aussi grande que possible l’énergie pour toutes les autres réponses. Cependant, cette perte n’empêche pas la fonction de donner la même valeur à chaque réponse incorrecte $Y^i$, donc dans ce sens, c’est une mauvaise fonction de perte pour les systèmes non linéaires. Pour améliorer cette perte, nous définissons la réponse incorrecte la plus offensante.

Perte de marge généralisée

Réponse incorrecte la plus offensante : cas discret
Soit $Y$ une variable discrète. Ensuite, pour un jeu d’entraînement $(X^i,Y^i)$, la réponse incorrecte la plus offensante $\bar Y^i$ est la réponse qui a la plus faible énergie parmi toutes les réponses possibles qui sont incorrectes :

Réponse incorrecte la plus offensante : cas continu
Soit $Y$ une variable continue. Ensuite, pour un échantillon d’entraînement $(X^i,Y^i)$, la réponse incorrecte la plus offensante $\bar Y^i$ est la réponse qui a la plus faible énergie parmi toutes les réponses qui sont au moins à $\epsilon$ de la bonne réponse :

Dans le cas discret, la réponse incorrecte la plus offensante est celle dont l’énergie est la plus faible et qui n’est pas la bonne réponse. Dans le cas continu, l’énergie pour $Y$ extrêmement proche de $Y^i$ devrait être proche de $E(W,Y^i,X^i)$. De plus, le $\text{argmin}$ évalué sur $Y$ non égal à $Y^i$ serait $0$. En conséquence, nous choisissons une distance $\epsilon$ et décidons que seul $Y$ est au moins $\epsilon$ de $Y_i$ doit être considéré comme la mauvaise réponse. C’est pourquoi l’optimisation ne porte que sur les $Y$ de distance au moins égale à $\epsilon$ de $Y^i$.

Si la fonction d’énergie est capable de garantir que l’énergie de la réponse incorrecte la plus offensante est supérieure à l’énergie de la bonne réponse d’une certaine marge, alors cette fonction d’énergie devrait bien fonctionner.

Exemples de fonctions de perte de marge généralisée

Perte Hinge

où $\bar Y^i$ est la réponse incorrecte la plus offensante. Cette perte impose que la différence entre la bonne réponse et la réponse incorrecte la plus offensante soit d’au moins $m$.

Figure 4 : Perte Hinge

Comment choisir $m$ ?

C’est arbitraire, mais cela affecte les poids de la dernière couche.

Log Loss

On peut considérer cela comme une Hinge Loss douce. Cette perte tente d’imposer une marge infinie, mais en raison de la décroissance exponentielle de la pente, cela ne se produit pas.

Figure 5 : Log Loss

Square-Square Loss

Cette perte combine le carré de l’énergie avec une hinge au carrée. La combinaison tente de minimiser l’énergie et d’appliquer une marge d’au moins $m$ à la mauvaise réponse la plus offensante. Cette méthode est très similaire à la perte utilisée dans les réseaux siamois.

Autres pertes

Il y en a tout un tas. Voici un résumé de bonnes et mauvaises fonctions de perte.

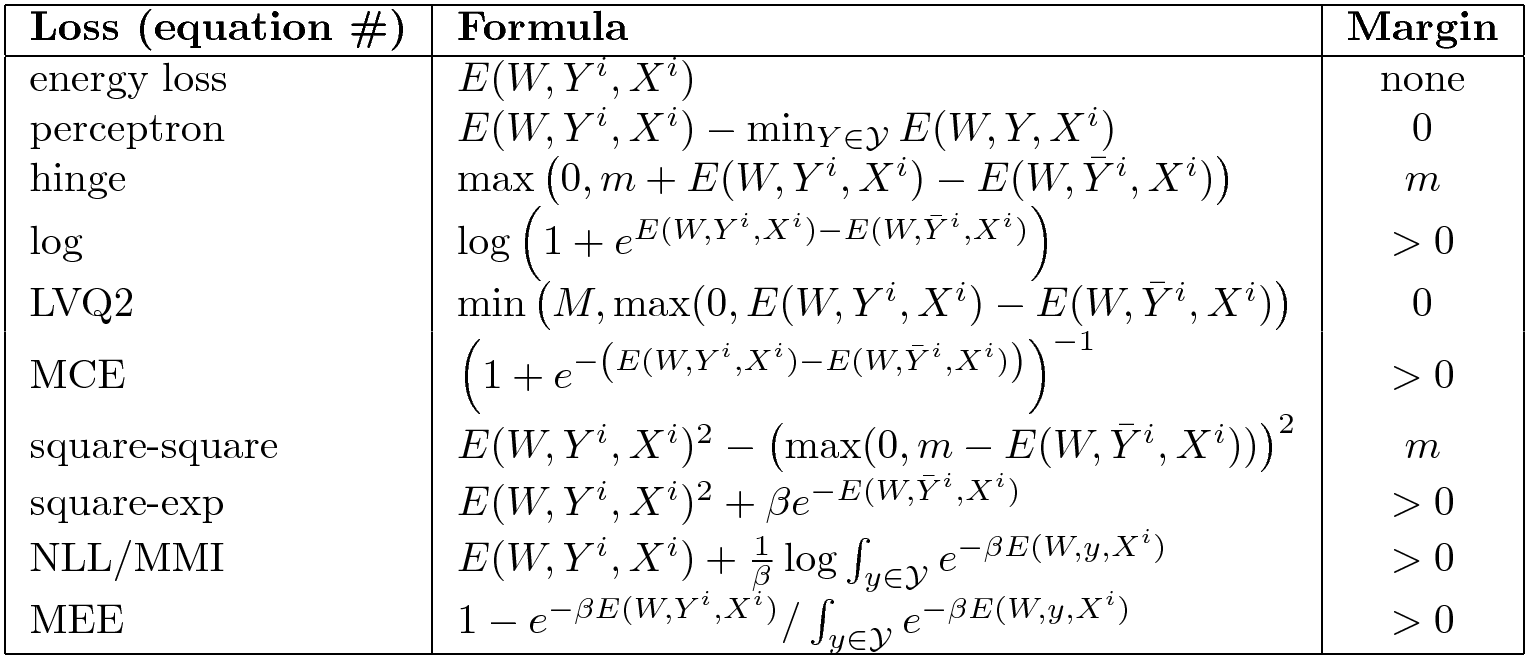
Figure 6 : Sélection des fonctions de perte d’EBM

La colonne de droite indique si la fonction d’énergie impose une marge. La simple perte d’énergie ne pousse nulle part donc elle n’a pas de marge. La perte d’énergie ne fonctionne pas pour tous les problèmes. La perte de perceptron fonctionne si nous avons une paramétrisation linéaire de notre énergie mais pas en général. Certaines ont une marge finie comme la perte hinge et d’autres une marge infinie comme la charnière souple.

Comment la réponse incorrecte la plus offensante trouve-t-elle $\bar Y_i$ dans le cas continu ?

Vous voulez pousser sur un point qui est suffisamment éloigné de $Y^i$ car s’il est trop proche, les paramètres peuvent ne pas bouger beaucoup puisque la fonction définie par un réseau neuronal est « raide ». Mais en général, c’est difficile et c’est le problème que les méthodes de sélection d’échantillons contrastifs tentent de résoudre. Il n’y a pas une seule façon correcte de le faire.

Une forme un peu plus générale pour les pertes contrastives de type hinge est :

Nous supposons que $Y$ est discret, mais s’il était continu, la somme serait remplacée par une intégrale. Ici, $E(W, Y^i,X^i)-E(W,y,X^i)$ est la différence entre $E$ évaluée à la bonne réponse et une autre réponse. $C(Y^i,y)$ est la marge et est généralement une mesure de distance entre $Y^i$ et $y$. La motivation est que le montant que nous voulons pousser vers le haut sur un échantillon incorrect $y$ devrait dépendre de la distance entre $y$ et l’échantillon correct $Y_i$. Il peut s’agir d’une perte plus difficile à optimiser.