Réseau convolutif pour graphe III

Introduction au réseau convolutif pour graphe

Le réseau convolutif pour graphe (GCN pour Graph Convolutional Network) est un type d’architecture qui utilise la structure des données. Avant d’entrer dans les détails, faisons un rapide rappel sur l’auto-attention car le GCN et l’auto-attention sont conceptuellement pertinents.

Récapitulatif sur l’auto-attention

• Dans l’auto-attention, nous avons un ensemble d’entrées $\lbrace\boldsymbol{x}_{i}\rbrace^{t}_{i=1}$. Contrairement à une séquence, elle n’a pas d’ordre.
• Le vecteur caché $\boldsymbol{h}$ est donné par une combinaison linéaire des vecteurs de l’ensemble.
• Nous pouvons l’exprimer sous la forme $\boldsymbol{X}\boldsymbol{a}$ en utilisant une multiplication matricielle des vecteurs, où $\boldsymbol{a}$ contient des coefficients qui mettent à l’échelle le vecteur d’entrée $\boldsymbol{x}_{i}$.

Pour une explication détaillée, voir les notes de la semaine 12.

Notation

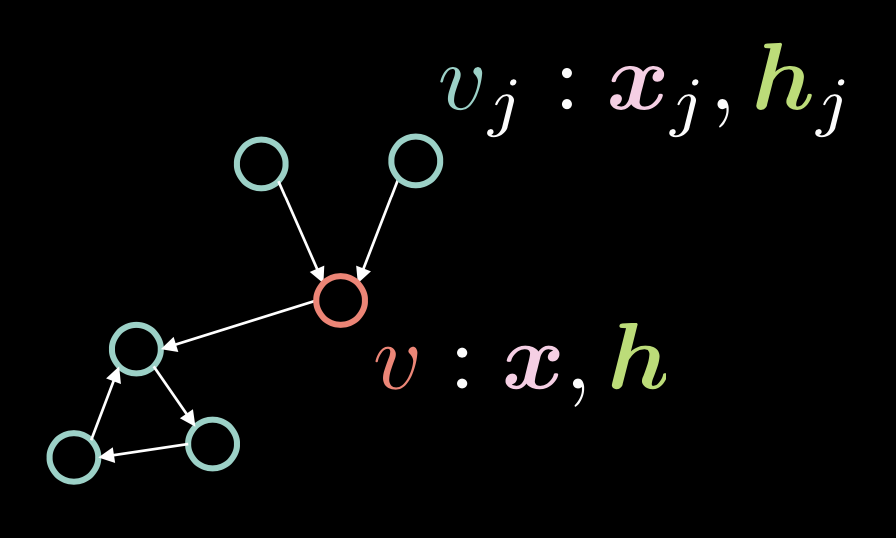
Figure 1 : ConvNet pour graphe

Dans la figure 1, le sommet $v$ est composé de deux vecteurs : l’entrée $\boldsymbol{x}$ et sa représentation cachée $\boldsymbol{h}$. Nous avons également plusieurs sommets $v_{j}$, qui se composent de $\boldsymbol{x}_j$ et de $\boldsymbol{h}_j$. Dans ce graphe, les sommets sont reliés par des arêtes dirigées.

Nous représentons ces arêtes dirigées avec le vecteur d’adjacence $\boldsymbol{a}$, où chaque élément $\alpha_{j}$ est fixé à $1$ s’il y a une arête dirigée de $v_{j}$ à $v$.

Le degré (nombre d’arêtes entrantes) $d$ est défini comme la norme de ce vecteur de’adjacence, c’est-à-dire $\Vert\boldsymbol{a}\Vert_{1} $, qui est le nombre de 1 dans le vecteur $\boldsymbol{a}$.

Le vecteur caché $\boldsymbol{h}$ est donné par l’expression suivante :

où $f(\cdot)$ est une fonction non linéaire telle que ReLU $(\cdot)^{+}$, Sigmoïde $\sigma(\cdot)$ et tangente hyperbolique $\tanh(\cdot)$.

Le terme $\boldsymbol{U}\boldsymbol{x}$ prend en compte le sommet $v$ lui-même en appliquant la rotation $\boldsymbol{U}$ à l’entrée $v$.

Dans l’auto-attention, le vecteur caché $\boldsymbol{h}$ est calculé par $\boldsymbol{X}\boldsymbol{a}$, ce qui signifie que les colonnes dans $\boldsymbol{X}$ sont mises à l’échelle par les facteurs dans $\boldsymbol{a}$. Dans le contexte du GCN, cela signifie que si nous avons plusieurs arêtes entrantes, c’est-à-dire plusieurs dans le vecteur d’adjacence $\boldsymbol{a}$, $\boldsymbol{X}\boldsymbol{a}$ s’agrandit. En revanche, si nous n’avons qu’une seule arête entrante, cette valeur devient plus petite. Pour remédier à ce problème de proportionnalité de la valeur par rapport au nombre d’arêtes entrantes, nous la divisons par le nombre d’arêtes entrantes $d$. Nous appliquons ensuite la rotation $\boldsymbol{V}$ à $\boldsymbol{X}\boldsymbol{a}d^{-1}$.

Nous pouvons représenter cette représentation cachée $\boldsymbol{h}$ pour l’ensemble des entrées $\boldsymbol{x}$ en utilisant la notation matricielle suivante :

où $\vect{D} = \text{diag}(d_{i})$.

Théorie et code du GCN résiduel à porte

Le GCN résiduel à porte (RG CGN pour Residual Gated GCN) est un type de GCN qui peut être représenté comme le montre la figure 2 :

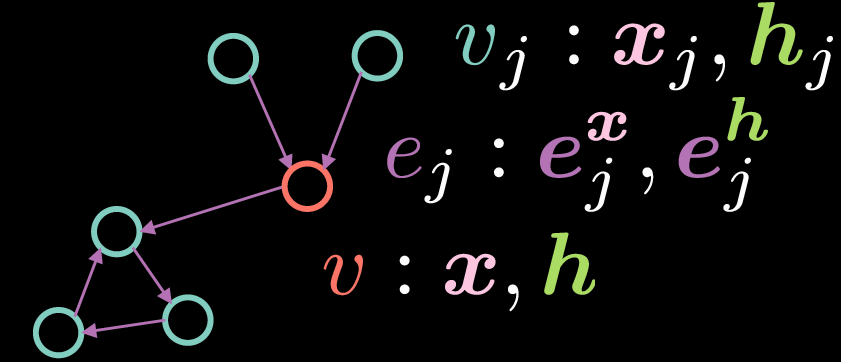
Figure 2 : GCN résiduel à porte

Comme pour le GCN standard, le sommet $v$ est constitué de deux vecteurs : l’entrée $\boldsymbol{x}$ et sa représentation cachée $\boldsymbol{h}$. Toutefois, dans ce cas, les arêtes ont également une représentation de caractéristique, où $\boldsymbol{e_{j}^{x}}$ représente la représentation de l’arête d’entrée et $\boldsymbol{e_{j}^{h}}$ représente la représentation de l’arête cachée.

La représentation cachée $\boldsymbol{h}$ du sommet $v$ est calculée par l’équation suivante :

où $\boldsymbol{x}$ est la représentation de l’entrée, $\boldsymbol{Ax}$ représente une rotation appliquée à l’entrée $\boldsymbol{x}$ et $\sum_{v_j→v}{\eta(\boldsymbol{e_{j}})\odot \boldsymbol{Bx_{j}}}$ indique la somme des multiplications par éléments des éléments entrants ayant subi une rotation $\boldsymbol{Bx_{j}}$ et d’une porte $\eta(\boldsymbol{e_{j}})$. Contrairement au GCN standard ci-dessus où nous faisons la moyenne des représentations entrantes, le terme de porte est essentiel à la mise en œuvre du RG CGN car il nous permet de moduler les représentations des entrées en fonction des représentations des arêtes.

A noter que la sommation se fait uniquement sur les sommets ${v_j}$ qui ont des arêtes entrantes au sommet ${v}$. Le terme résiduel (dans Residual Gated GCN) vient du fait que pour calculer la représentation cachée $\boldsymbol{h}$, on ajoute la représentation d’entrée $\boldsymbol{x}$. Le terme de porte $\eta(\boldsymbol{e_{j}})$ est calculé comme indiqué ci-dessous :

La valeur de porte $\eta(\boldsymbol{e_{j}})$ est une sigmoïde normalisée obtenue en divisant la sigmoïde de la représentation de l’arête entrante par la somme des sigmoïdes de toutes les représentations de l’arête entrante. A noter que pour calculer le terme de porte, nous avons besoin de la représentation de l’arête $\boldsymbol{e_{j}}$, qui peut être calculée à l’aide des équations ci-dessous :

La représentation des arêtes cachées $\boldsymbol{e_{j}^{h}}$ est obtenue par la sommation de la représentation initiale des arêtes $\boldsymbol{e_{j}^{x}}$ et $\texttt{ReLU}(\cdot)$ appliqué à $\boldsymbol{e_{j}}$ où $\boldsymbol{e_{j}}$ est à son tour donné par la somme d’une rotation appliquée à $\boldsymbol{e_{j}^{x}}$, une rotation appliquée à la représentation en entrée $\boldsymbol{x_{j}}$ du sommet $v_{j}$ et une rotation appliquée à la représentation en entrée $\boldsymbol{x}$ du sommet $v$.

Note : afin de calculer les représentations cachées en aval (par exemple la deuxième couche de représentations cachées), nous pouvons simplement remplacer les représentations des caractéristiques d’entrée par les représentations des caractéristiques de la couche première dans les équations au-dessus.

Graph Classification et couche GCN résiduelle

Pour cette section et dans la suite, les codes se réfèrent au notebook Jupyter dont la version anglaise est disponible ici et la version française ici.

Dans cette section, nous introduisons le problème de la classification des graphes et codons une couche GCN résiduelle. En plus des déclarations d’importation habituelles, nous ajoutons ce qui suit :

os.environ['DGLBACKEND'] = 'pytorch'
import dgl
from dgl import DGLGraph
from dgl.data import MiniGCDataset
import networkx as nx

La première ligne indique à Deep Graph Library (DGL) d’utiliser PyTorch comme backend. DGL fournit diverses fonctionnalités sur les graphes alors que networkx nous permet de visualiser les graphes.

Dans ce notebook, la tâche consiste à classer une structure de graphe donnée dans l’un des 8 types de graphes. Le jeu de données obtenu à partir de dgl.data.MiniGCDataset donne un certain nombre de graphes (num_graphs) avec des nœuds entre min_num_v et max_num_v. Par conséquent, tous les graphes obtenus n’ont pas le même nombre de nœuds/sommets.

Note : afin de vous familiariser avec les bases des DGLGraphs, il est recommandé de suivre le court tutoriel (en anglais) disponible ici.

Après avoir créé les graphes, la tâche suivante consiste à ajouter un signal au domaine. Des caractéristiques peuvent être appliquées aux nœuds et aux arêtes d’un DGLGraph. Les caractéristiques sont représentées par un dictionnaire de noms (chaînes de caractères) et de tenseurs (champs). Les ndata et edata sont des sucres syntaxiques permettant d’accéder aux données des caractéristiques de tous les nœuds et arêtes.

L’extrait de code suivant montre comment les caractéristiques sont générées. Chaque nœud se voit attribuer une valeur égale au nombre d’arêtes incidentes, tandis que chaque bord se voit attribuer la valeur 1.

def create_artificial_features(dataset):
    for (graph, _) in dataset:
        graph.ndata['feat'] = graph.in_degrees().view(-1, 1).float()
        graph.edata['feat'] = torch.ones(graph.number_of_edges(), 1)
    return dataset

Des jeux de données d’entraînement et de test sont créés et des caractéristiques sont attribuées comme indiqué ci-dessous :

trainset = MiniGCDataset(350, 10, 20)
testset = MiniGCDataset(100, 10, 20)

trainset = create_artificial_features(trainset)
testset = create_artificial_features(testset)

Un exemple de graphe issu du jeu d’entraînement a la représentation suivante. Ici, nous observons que le graphe a 15 nœuds et 45 arêtes et que les nœuds et les arêtes ont une représentation caractéristique de la forme (1,) comme prévu. De plus, le 0 signifie que ce graphe appartient à la classe 0.

(DGLGraph(num_nodes=15, num_edges=45,
         ndata_schemes={'feat': Scheme(shape=(1,), dtype=torch.float32)}
         edata_schemes={'feat': Scheme(shape=(1,), dtype=torch.float32)}), 0)

Note sur le message DGL et les fonctions de réduction

Dans DGL, les fonctions de message sont exprimées sous la forme de Edge UDFs (User Defined Functions : fonctions définies par l’utilisateur). Les Edge UDFs prennent en compte un seul argument edges (arêtes). Il a trois membres src, dst et data pour accéder respectivement aux fonctions du nœud source, du nœud de destination et des fonctions des arêtes. Les fonctions de réduction sont des Node UDFs. Les node UDFs ont un seul argument nodes, qui a deux membres data et mailbox. data contient les caractéristiques du nœud et mailbox contient toutes les caractéristiques des messages entrants, empilées le long de la seconde dimension (d’où l’argument dim=1). update_all(message_func, reduce_func) envoie les messages par toutes les arêtes et met à jour tous les nœuds.

Implémentation de la couche GR GCN

Une couche GR GCN est implémentée comme indiqué dans les extraits de code ci-dessous.

Premièrement, toutes les rotations des caractéristiques d’entrée $\boldsymbol{Ax}$, $\boldsymbol{Bx_{j}}$, $\boldsymbol{Ce_{j}^{x}}$, $\boldsymbol{Dx_{j}}$ et $\boldsymbol{Ex}$ sont calculées en définissant nn.Linear couches à l’intérieur de la fonction __init__ puis en propageant les représentations d’entrée h et e à travers les couches linéaires à l’intérieur de la fonction forward.

class GatedGCN_layer(nn.Module):

    def __init__(self, input_dim, output_dim):
        super().__init__()
        self.A = nn.Linear(input_dim, output_dim)
        self.B = nn.Linear(input_dim, output_dim)
        self.C = nn.Linear(input_dim, output_dim)
        self.D = nn.Linear(input_dim, output_dim)
        self.E = nn.Linear(input_dim, output_dim)
        self.bn_node_h = nn.BatchNorm1d(output_dim)
        self.bn_node_e = nn.BatchNorm1d(output_dim)

Deuxièmement, nous calculons les représentations de l’arête. Ceci est fait à l’intérieur de la fonction message_func, qui itère sur toutes les arêtes et calcule leurs représentations. Plus précisément, la ligne e_ij = edges.data['Ce'] + edges.src['Dh'] + edges.dst['Eh'] calcule (Eq. 7) à partir du haut. La fonction message_func envoie Bh_j (qui est $\boldsymbol{Bx_{j}}$ de (Eq. 5)) et e_ij (Eq. 7) par le bord dans la boîte aux lettres du noeud de destination.

def message_func(self, edges):
    Bh_j = edges.src['Bh']
    # e_ij = Ce_ij + Dhi + Ehj
    e_ij = edges.data['Ce'] + edges.src['Dh'] + edges.dst['Eh']
    edges.data['e'] = e_ij
    return {'Bh_j' : Bh_j, 'e_ij' : e_ij}

Troisièmement, la fonction reduce_func collecte les messages envoyés par la fonction message_func. Après avoir collecté les données du nœud Ah et les données expédiées Bh_j et e_ij de la mailbox, la ligne h = Ah_i + torch.sum(sigma_ij * Bh_j, dim=1) / torch.sum(sigma_ij, dim=1) calcule la représentation cachée de chaque nœud comme indiqué dans (Eq. 5). A noter cependant que cela ne représente que le terme $(\boldsymbol{Ax} + \sum_{v_j→v}{\eta(\boldsymbol{e_{j}})\odot \boldsymbol{Bx_{j}}})$ sans le $\texttt{ReLU}(\cdot)$ et la connexion résiduelle.

def reduce_func(self, nodes) :
    Ah_i = nodes.data [Ah]
    Bh_j = nodes.mailbox['Bh_j']
    e = nœuds.boîte aux lettres [e_ij]
    # sigma_ij = sigmoid(e_ij)
    sigma_ij = torche.sigmoid(e)
    # hi = Ahi + sum_j eta_ij * Bhj
    h = Ah_i + torch.sum(sigma_ij * Bh_j, dim=1) / torch.sum(sigma_ij, dim=1)
    return {'h' : h}

A l’intérieur de la fonction forward, ayant appelé g.update_all, nous obtenons les résultats de la convolution des graphes h et e, qui représentent les termes $(\boldsymbol{Ax} + \sum_{v_j→v}{\eta(\boldsymbol{e_{j}})\odot \boldsymbol{Bx_{j}}})$ de (Eq.5) et $\boldsymbol{e_{j}}$ de (Eq. 7) respectivement. Ensuite, nous normalisons h et e par rapport à la taille du nœud et de l’arête du graphe respectivement. La batch normalisation est ensuite appliquée afin que nous puissions entraîner le réseau efficacement. Enfin, nous appliquons $\texttt{ReLU}(\cdot)$ et ajoutons les connexions résiduelles pour obtenir les représentations cachées des nœuds et des arêtes, qui sont ensuite renvoyées par la fonction forward.

def forward(self, g, h, e, snorm_n, snorm_e) :

    h_in = h # connexion résiduelle
    e_in = e # connexion résiduelle

    g.ndata [h] = h
    g.ndata ["Ah"] = self.A(h)
    g.ndata [Bh] = self.B(h)
    g.ndata [Dh] = self.D(h)
    g.ndata ["Eh"] = self.E(h)
    g.edata ["e"] = e
    g.edata ["Ce"] = self.C(e)

    g.update_all(self.message_func, self.reduce_func)

    h = g.ndata [h] # résultat de la convolution du graphe
    e = g.edata['e'] # résultat de la convolution du graphe

    h = h * snorm_n # normalisation de l'activation par rapport à la taille des noeuds du graphe
    e = e * snorm_e # normalisation de l'activation par rapport à la taille des arêtes du graphe

    h = self.bn_node_h(h) # batch normalisation
    e = self.bn_node_e(e) # batch normalisation

    h = torch.relu(h) # activation non linéaire
    e = torch.relu(e) # activation non linéaire

    h = h_in + h # connexion résiduelle
    e = e_in + e # connexion résiduelle

     return h, e

Ensuite, nous définissons le module MLP_Layer qui contient plusieurs couches entièrement connectées. Nous créons une liste de couches entièrement connectées et nous les transmettons à travers le réseau.

Enfin, nous définissons notre modèle GatedGCN qui comprend les classes définies précédemment : GatedGCN_layer et MLP_layer. La définition de notre modèle (GatedGCN) est présentée ci-dessous.

 class GatedGCN(nn.Module):
    def __init__(self, input_dim, hidden_dim, output_dim, L):
        super().__init__()
        self.embedding_h = nn.Linear(input_dim, hidden_dim)
        self.embedding_e = nn.Linear(1, hidden_dim)
        self.GatedGCN_layers = nn.ModuleList([
            GatedGCN_layer(hidden_dim, hidden_dim) for _ in range(L)
        ])
        self.MLP_layer = MLP_layer(hidden_dim, output_dim)
    def forward(self, g, h, e, snorm_n, snorm_e):
        # enchâssement en entrée
        h = self.embedding_h(h)
        e = self.embedding_e(e)
        # couche GCN
        for GGCN_layer in self.GatedGCN_layers:
            h, e = GGCN_layer(g, h, e, snorm_n, snorm_e)
        # classifieur MLP
        g.ndata['h'] = h
        y = dgl.mean_nodes(g,'h')
        y = self.MLP_layer(y)
        return y

Dans notre constructeur, nous définissons les enchâssements pour e et h (self.embedding_e et self.embedding_h), self.GatedGCN_layers qui est la liste (de taille $L$) de notre modèle précédemment défini : GatedGCN_layer, et enfin self.MLP_layer qui a également été défini auparavant. Ensuite, en utilisant ces initialisations, nous faisons simplement avancer le modèle et nous obtenons un y.

Pour mieux comprendre le modèle, nous initialisons un objet du modèle et l’affichons pour une meilleure visualisation :

model = GatedGCN(input_dim=1, hidden_dim=100, output_dim=8, L=2)
print(model)

La structure principale du modèle est présentée ci-dessous :

GatedGCN(
  (embedding_h): Linear(in_features=1, out_features=100, bias=True)
  (embedding_e): Linear(in_features=1, out_features=100, bias=True)
  (GatedGCN_layers): ModuleList(
    (0): GatedGCN_layer(...)
    (1): GatedGCN_layer(... ))
  (MLP_layer): MLP_layer(
    (FC_layers): ModuleList(...))

Sans surprise, nous avons deux couches de GatedGCN_layer (puisque L=2) suivies d’une MLP_layer qui donne finalement une sortie de 8 valeurs.

Ensuite, nous définissons nos fonctions train et evaluate. Dans notre fonction train, nous avons notre code générique qui prend des échantillons dans le dataloader. Ensuite, les batch_graphs, batch_x, batch_e, batch_snorm_n et batch_snorm_e sont introduits dans notre modèle qui retourne des batch_scores (de taille 8). Les scores prédits sont comparés à la vérité de base dans notre fonction de perte : loss(batch_scores, batch_labels). Ensuite, nous mettons à zéro les gradients (optimizer.zero_grad()), nous effectuons une rétropropagation (J.backward()) et nous mettons à jour nos poids (optimizer.step()). Enfin, la perte pour l’époque et la précision de l’entraînement est calculée. Nous utilisons un code similaire pour notre fonction evaluate.

Enfin, nous sommes prêts à pour l’entraînement ! Nous pouvons constater qu’après $40$ époques d’entraînement, notre modèle a appris à classer les graphes avec une précision de test de $87$%.