Réseau convolutif pour graphe II

Réseaux convolutifs pour graphe (GCNs) spectraux

Dans la partie du cours précédente, nous avons discuté de la théorie spectrale des graphes et de l’une des deux façons de définir la convolution des graphes que nous pouvons maintenant utiliser pour définir les GCNs spectraux.

GCN spectral standard

Nous définissons une couche convolutionnelle spectrale pour graphe telle que, étant donnée la couche $h^l$, l’activation de la couche suivante est :

où $\eta$ représente une activation non linéaire et $w^l$ est un filtre spatial. Le côté droit de l’équation est équivalent à $\eta(\hat{w}^l(\Delta)h^l)$ où $\hat{w}^l$ représente un filtre spectral et $\Delta$ est le Laplacien. Nous pouvons ensuite décomposer le côté droit de l’équation en $\eta(\boldsymbol{\phi} \hat{w}^l(\Lambda)\boldsymbol{\phi^\top} h^l)$, où $\boldsymbol{\phi}$ est la matrice de Fourier et $\Lambda$ sont les valeurs propres. On obtient ainsi l’équation d’activation finale suivante :

L’objectif est d’apprendre le filtre spectral $\hat{w}^l(\lambda)$ en utilisant la rétropropagation au lieu de la conception manuelle.

Cette technique a été la première technique spectrale utilisée pour les ConvNets, mais elle présente quelques limites :

• Aucune garantie de localisation spatiale des filtres.
• Besoin d’apprendre les paramètres $O(n)$ par couche ($\hat{w}(\lambda_1)$ à $\hat{w}(\lambda_n)$).
• Le taux d’apprentissage est de $O(n^2$) car $\boldsymbol{\phi}$ est une matrice dense.

Les SplineGCNs

Les SplineGCNs impliquent le calcul de filtres spectraux lisses pour obtenir des filtres spatiaux localisés. Le lien entre le lissage dans le domaine fréquentiel et la localisation dans l’espace est basé sur l’égalité de Parseval : plus petite dérivée du filtre spectral (fonction de lissage) $\Leftrightarrow$ plus petite variance du filtre spatial (localisation).

Comment obtenir un filtre spectral plus lisse ? Nous décomposons le filtre spectral pour obtenir une combinaison linéaire de $K$ noyaux lisses $\boldsymbol{B}$ (splines) de sorte que $\hat{w}^l(\Lambda)=diag(\boldsymbol{B}w^l)$. L’équation d’activation est la suivante :

Maintenant, nous n’avons que des paramètres $O(1)$ ($K$ constants) par couche à apprendre par rétropropagation. Cependant, la complexité de l’apprentissage est toujours de $O(n^2)$.

LapGCNs

Comment apprenons-nous en temps linéaire $O(n)$ (taille du graphe par rapport à $n$) ? La complexité $O(n^2)$ est le résultat direct de l’utilisation de vecteurs propres laplaciens. Nous devons éviter la décomposition propre, qui peut être réalisée en apprenant directement une fonction du Laplacien. La fonction spectrale est un monôme du Laplacien comme montré ici :

Une caractéristique intéressante est que les filtres sont localisés exactement dans les supports k-hop.

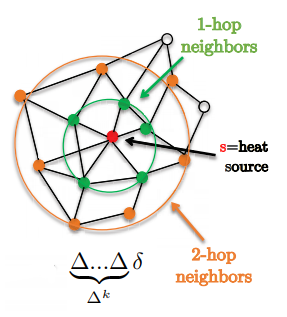
Figure 1 : Voisinages à 1 et 2 sauts

Nous remplaçons l’expression $\Delta^kh$ par $X_k$, une équation récursive définie comme :

La complexité est maintenant de $O(E.K)=O(n)$ pour les graphes épars (du monde réel). Nous pouvons remodeler $X_k$ en $\bar{X}$ pour former une opération linéaire. Nous avons maintenant l’équation d’activation suivante :

Note : comme aucune décomposition propre laplacienne n’est utilisée, toutes les opérations se situent dans le domaine spatial (et non spectral). Il peut donc être erroné de les appeler GCNs spectraux. En outre, un autre inconvénient des LapGCNs est que les couches convolutionnelles impliquent des opérations linéaires éparses pour lesquelles les GPUs ne sont pas totalement optimisés.

Nous avons maintenant résolu les 3 limitations des GCNs standards grâce à des filtres localisés (en support $K$-hop), $O(1)$ paramètres par couche et $O(n)$ complexité d’apprentissage. Cependant, la limitation des GCNs standards est que la base monomiale ($\Delta^0,\Delta^1,\ldots$) utilisée est instable pour l’optimisation car elle n’est pas orthogonale (la modification d’un coefficient modifie l’approximation de la fonction).

ChebNets

Pour résoudre la question de la base instable, nous pouvons utiliser n’importe quelle base orthonormée, mais elle doit avoir une équation récursive pour assurer une complexité linéaire. Pour les ChebNets, nous utilisons des polynômes de Tchebyshev, et comme dans un LapGCN, nous représentons l’expression $T_k(\Delta)h$ (fonction de Tchebyshev appliquée à $h$) par $X_k$, une équation récursive définie comme :

Nous avons maintenant une stabilité sous l’effet de la perturbation du coefficient.

Les ChebNets sont des GCNs qui peuvent être utilisés pour n’importe quel domaine de graphe arbitraire, mais la limitation est qu’ils sont isotropes. Les ConvNets standards produisent des filtres anisotropes car les grilles euclidiennes ont une direction, tandis que les GCNs spectraux calculent des filtres isotropes car les graphes n’ont pas de notion de direction (haut, bas, gauche, droite).

Nous pouvons étendre les ChebNets à plusieurs graphes en utilisant un filtre spectral 2D. Cela peut être utile, par exemple, dans les systèmes de recommandation où nous avons des graphes de films et des graphes d’utilisateurs. Les ChebNets multi-graphes ont l’équation d’activation suivante :

CayleyNets

Les ChebNets sont instables pour produire des filtres (localiser) avec des bandes de fréquences d’intérêt (communautés de graphes). Dans les CayleyNets, nous utilisons plutôt comme base orthonormée les rationnels de Cayley :

Les CayleyNets ont les mêmes propriétés que les ChebNets (sont isotropes), mais ils sont localisés en fréquence (avec un zoom spectral) et fournissent une classe de filtres plus riche (pour le même ordre de grandeur $K$).

GCNs spaciaux

Appariement de patrons

Pour comprendre les CGNs spaciaux, nous revenons à la définition des ConvNets via l’appariement de patrons.

Le problème principal lorsque nous effectuons l’appariement de patrons pour les graphes est l’absence d’ordre ou de positionnement des nœuds pour le modèle. Tout ce que nous avons, ce sont les indices des nœuds, ce qui ne suffit pas pour faire correspondre les informations entre eux. Comment pouvons-nous concevoir l’appariement de patrons de manière à ce qu’il soit invariant pour le reparamétrage des nœuds ? C’est-à-dire pas de modification si nous avons un graphe et changeons l’indice arbitraire de l’un des nœuds de, disons 6, à 122. Il est donc essentiel de pouvoir effectuer l’appariement de patrons indépendamment de l’index du nœud.

La façon la plus simple de le faire est d’avoir un seul vecteur de patron $w^l$, au lieu d’avoir $w_{j1}$, $w_{j2}$, $w_{j3}$ ou ainsi de suite. Nous faisons donc correspondre ce vecteur $w^l$ avec toutes les autres caractéristiques de notre graphe. La plupart des GNNs utilisent aujourd’hui cette propriété.

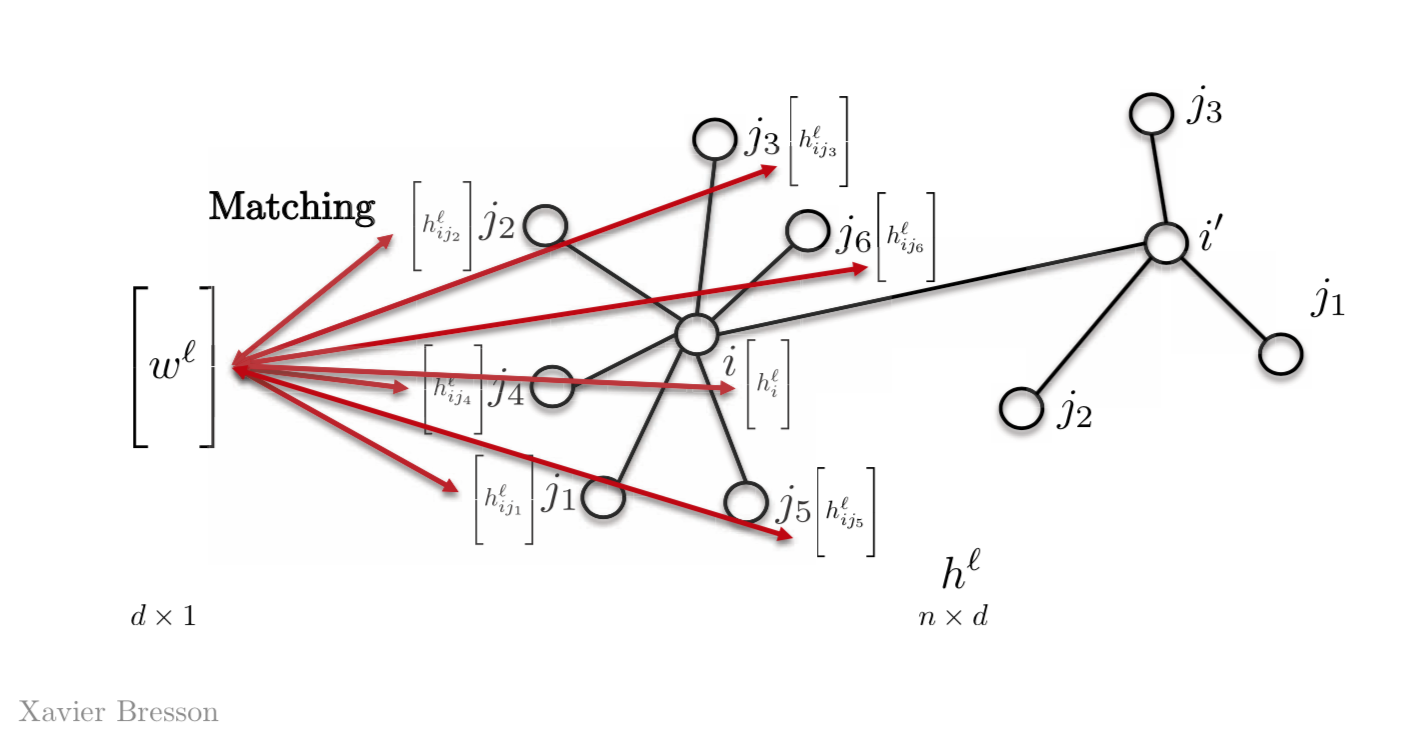
Figure 2 : L'appariement de patrons à l'aide d'un vecteur de patron

Mathématiquement, pour une caractéristique que nous avons :

où $w^l$ est le vecteur de patron au niveau de la couche $l$ de dimensions $d \times 1$ et $h_{ij}^l$ est le vecteur au niveau du nœud j avec $d \times 1$ ce qui donnera une quantité d’échelle $h_{i}^{l+1}$ au nœud $i$.

Pour ($d$) caractéristiques :

où $\boldsymbol{W}^l$ est de la dimension $d \times d$ et $h_{i}^{l+1}$ est $d \times 1$

Pour une représentation vectorielle :

où $\boldsymbol{A}$ est la matrice d’adjacence de dimensions $n \times n$, $h^l$ est la fonction d’activation à la couche $l$ de dimensions $n \times d$.

Sur la base de cette définition de l’appariement de patrons, nous pouvons définir deux types de GCNs spatiaux : les GCNs isotropes et les GCNs anisotropes.

Les GCNs isotropiques

GCNs spaciaux standards

Même définition qu’auparavant, mais nous ajoutons la matrice diagonale dans l’équation, de telle sorte que nous trouvons la valeur moyenne du voisinage.

La représentation matricielle étant :

où, \boldsymbol{A} a les dimensions $n \times n$, $h^{l}$ a les dimensions $n \times d$ et $W^{l}$ a $d \times d$, ce qui donne une matrice $n \times d$ $h^{l+1}$.

Et la représentation vectorielle étant :

où, $h_{i}^{l+1}$ a les dimensions de $d \times 1$

La représentation vectorielle est responsable de la gestion de l’absence d’ordonnancement des nœuds, qui est invariante de la reparamétrisation des nœuds. C’est-à-dire, en ajoutant à l’exemple précédent, si le nœud en 6 et est changé en 122, cela ne changera rien dans le calcul de la fonction d’activation de la couche suivante $h^{l+1}$.

Nous pouvons également traiter des voisinages de tailles différentes. C’est-à-dire que nous pouvons avoir un voisinage de 4 nœuds ou de 10 nœuds, cela ne changera rien.

Le champ de réception local nous est donné par conception, c’est-à-dire qu’avec les GNNs, nous n’avons qu’à considérer les voisins.

Nous avons un partage de poids, c’est-à-dire que nous avons la même matrice $\boldsymbol{W}^{l}$ pour toutes les caractéristiques quelle que soit la position du graphe, qui est une propriété de convolution.

Cette formulation est également indépendante de la taille du graphe puisque toutes les opérations sont effectuées localement.

Comme il s’agit d’un modèle isotrope, les voisins auront la même matrice $\boldsymbol{W}^{l}$.

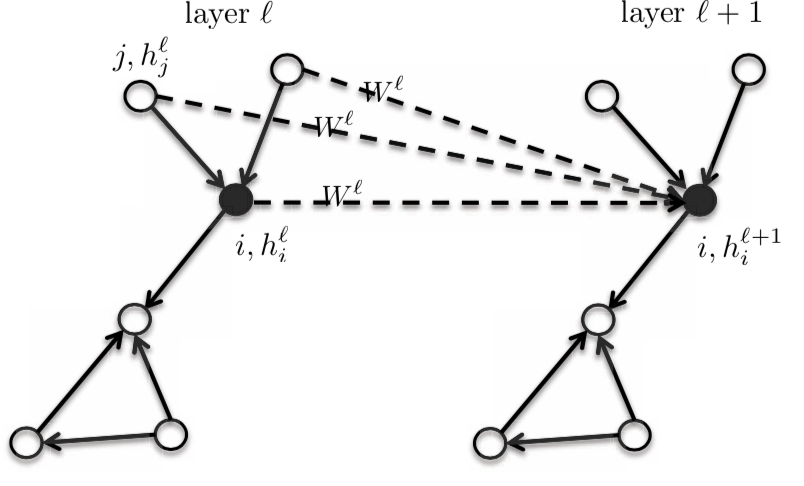
Figure 3 : Modèle isotrope

Ainsi, l’activation de la couche suivante $h_{i}^{l+1}$ est une fonction de l’activation de la couche précédente $h_{i}^{l}$ au nœud $i$ et au voisinage de $i$. Lorsque nous modifions la fonction, nous obtenons une famille entière de graphes.

ChebNets et GCNs spaciaux standards

Le GCN spatial standard défini ci-dessus est une simplification des ChebNets. Nous pouvons tronquer l’expansion de ChebNet en utilisant les deux premières fonctions de Chebyshev pour aboutir à :

GraphSage

Si la matrice d’adjacence $\boldsymbol{A}_{ij} = 1$ pour les arêtes dans les GCNs spatiaux standards, on obtient :

Pour cette équation, nous donnons au sommet central/cœur $i$ et à son voisinage le même poids de patron $\boldsymbol{W}^{l}$. Nous pouvons différencier cette équation en donnant au nœud central $\boldsymbol{W}_{1}^{l}$, et en ayant un nœud de patron différent $\boldsymbol{W}_{2}^{l}$ pour le voisinage one-hot. Cela permet d’améliorer considérablement les performances des GNNs. Ce modèle est toujours considéré comme étant de nature isotrope puisque les voisins ont le même poids.

où, $\boldsymbol{W}_{1}^{l}$ et $\boldsymbol{W}_{2}^{l}$ sont de dimension $d \times d$ ; $h_{i}^{l}$ et $h_{j}^{l}$ sont de dimension $d \times 1$.

Dans cette équation, on peut trouver la somme ou le maximum de $\boldsymbol{W}_{2}^{l} h_{j}^{l}$ ou la mémoire à long terme de $h_{j}^{l}$, au lieu de la moyenne.

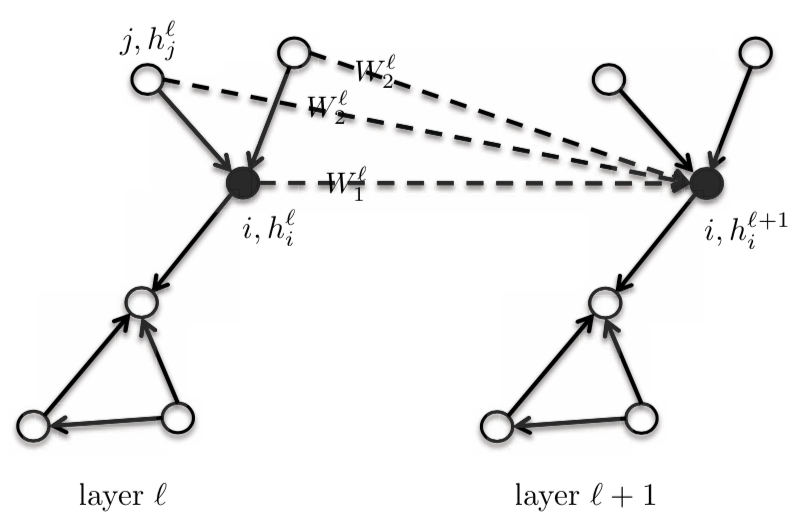
Figure 4 : GraphSage

Graph Isomorphism Networks (GIN)

Une architecture qui peut différencier les graphes qui ne sont pas isomorphiques. L’isomorphisme est la mesure de l’équivalence entre les graphes. Dans la figure ci-dessous, les deux graphes sont considérés comme isomorphes l’un par rapport à l’autre. Les graphes isomorphes seront traités de manière similaire et les graphes non isomorphes seront traités différemment.

Le GIN (Graph Isomorphism Networks) est un GCN isotrope.

où, $\texttt{BN}$ représente la normalisation par batch.

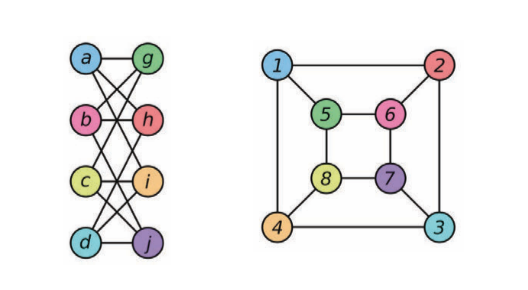
Figure 5 : Exemples de deux graphes isomorphes

GCNs anisotropes

Les ConvNets standards ont la capacité de produire des filtres anisotropes qui favorisent certaines directions. En effet, la structure directionnelle est basée sur le haut, le bas, la gauche et la droite. Cependant les ConvNets décrits ci-dessus n’ont aucune notion de direction et ne peuvent donc produire que des filtres isotropes. L’anisotropie peut être introduite naturellement avec des caractéristiques d’arêtes. Par exemple, les molécules peuvent avoir des liaisons simples, doubles et triples. Graphiquement, elle est introduite en pondérant différemment les différents voisins.

MoNets

Les MoNets utilisent le degré du graphe pour apprendre les paramètres d’un modèle de mélange gaussien.

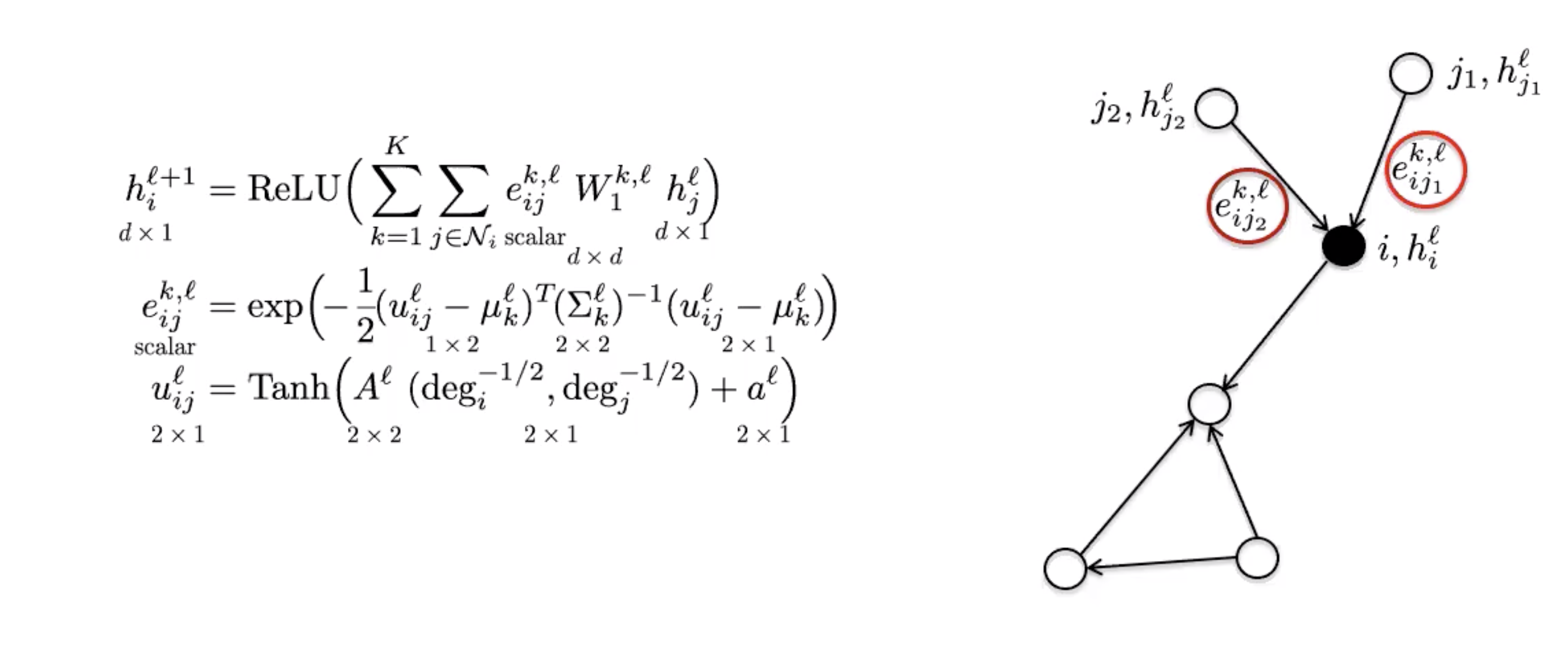
Figure 6 : MoNet

Graph Attention Networks (GATs)

Le GAT utilise le mécanisme d’attention pour introduire l’anisotropie dans la fonction d’agrégation du voisinage.

Figure 7 : GAT

GCNs à porte

Ils utilisent un simple mécanisme de porte. Cela peut être considéré comme un processus d’attention plus doux que le mécanisme d’attention épars utilisé dans les GATs.

Figure 8 : GCNs à porte

Graph Transformers

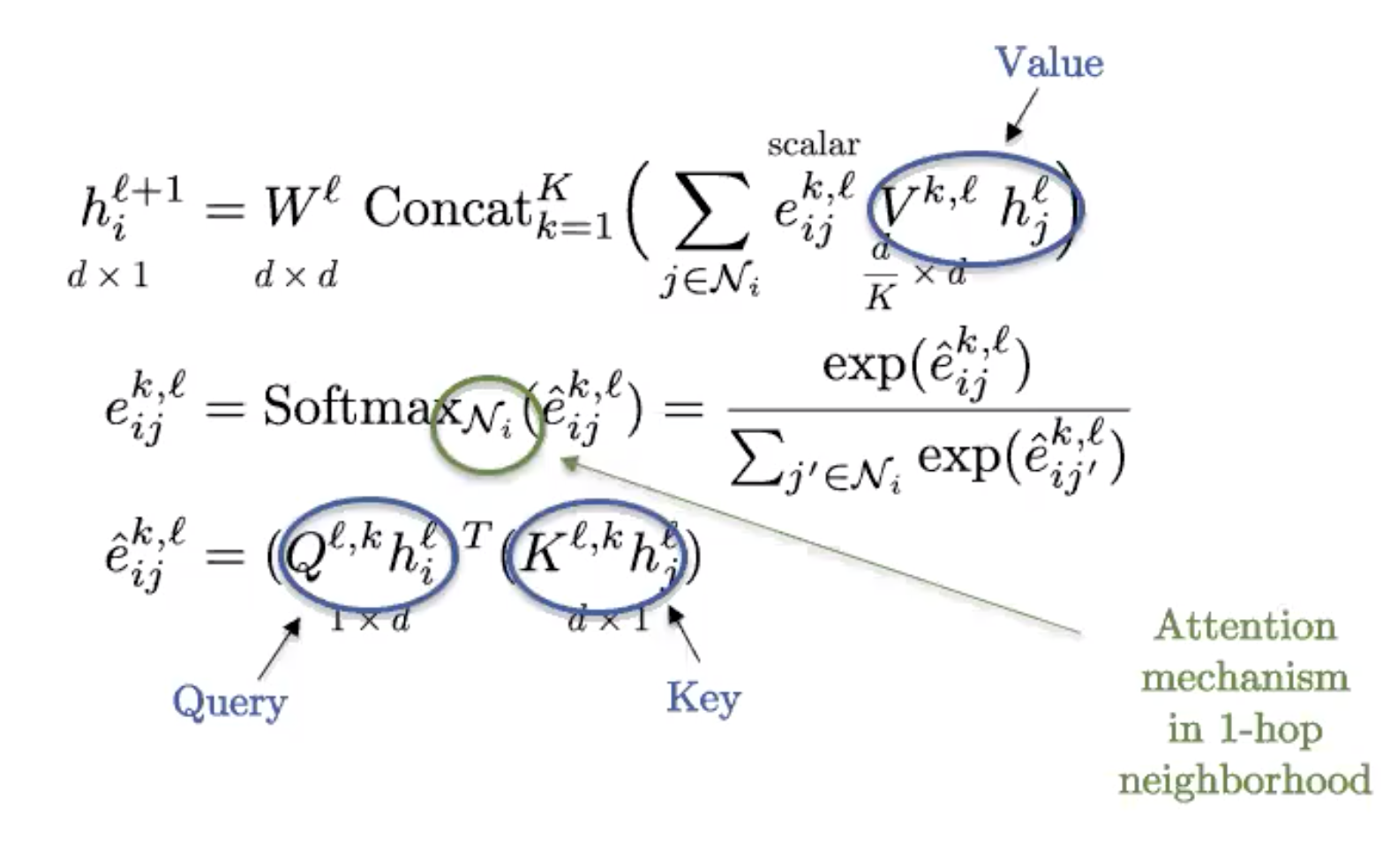
Figure 9 : Graph Transformer

Il s’agit de la version sous la forme d’un graphe du transformer standard communément utilisé en traitement du langage naturel. Si le graphe est entièrement connecté (tous les deux nœuds partagent une arête), on retrouve la définition d’un transformer standard.

Les graphes obtiennent leur structure à partir d’une éparsité, donc le graphe entièrement connecté a une structure triviale et est essentiellement un ensemble. Les transformers peuvent alors être considérés comme des réseaux de neurones Set et sont en fait la meilleure technique actuelle pour analyser des ensembles de caractéristiques.

Analyse comparative des GNNs

Les critères de référence sont un élément essentiel du progrès dans tout domaine. Le benchmark récemment publié Benchmarking Graph Neural Networks comporte six jeux de données à moyenne échelle qui peuvent être utilisés pour quatre problèmes fondamentaux des graphes : la classification de graphes, la régression de graphes, la classification des nœuds et la classification des arêtes. Bien que ces jeux de données soient de taille moyenne, ils sont suffisants pour séparer statiquement les tendances des différents réseaux de neurones des graphes.

À titre d’exemple de tâche de régression de graphes, nous voudrions prédire la solubilité moléculaire.

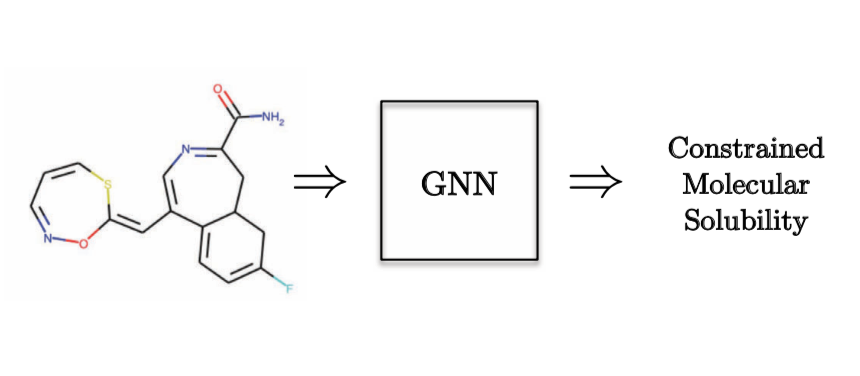
Figure 10 : Tâche de régression de graphes - Chimie quantique

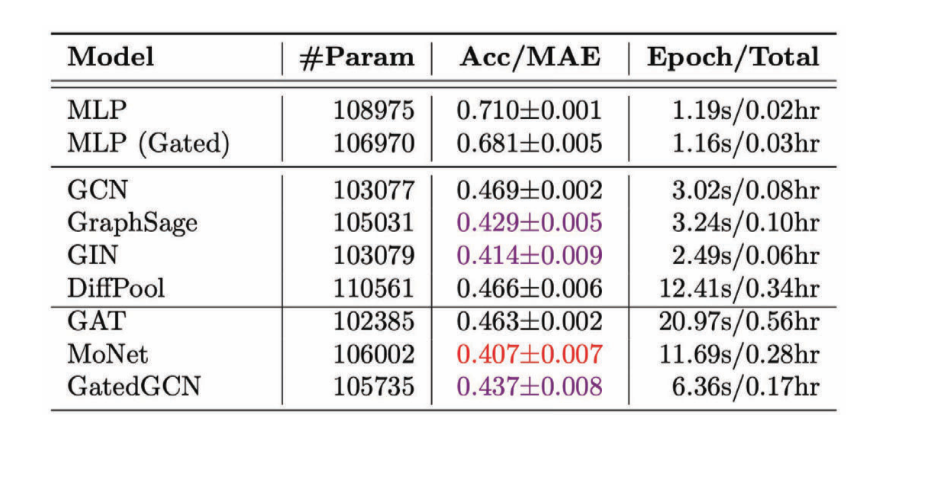
Figure 11 : Performance de divers GCNs sur la tâche de régression

Nous remarquons que dans la plupart des cas, les GCNs anisotropes ont de meilleures performances que les GCNs isotropes car nous utilisons des propriétés directionnelles.

Pour une tâche de classification de graphes, un problème de vision par ordinateur a été choisi où nous avons des super-nœuds d’images et nous voulons classifier l’image.

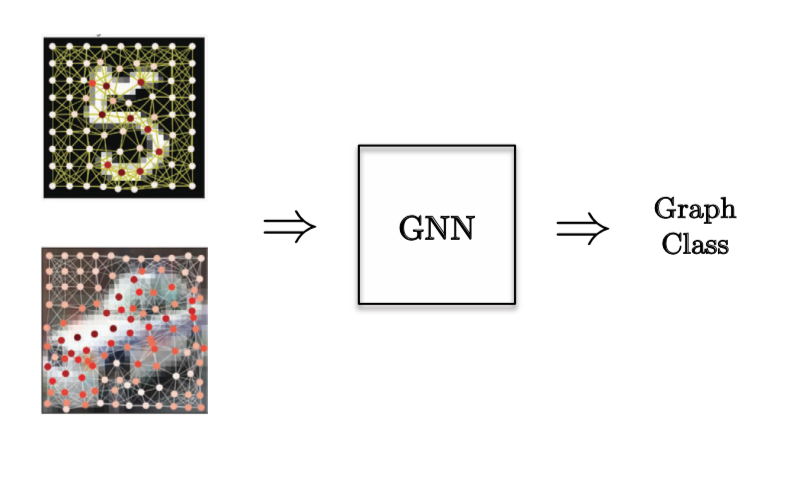
Figure 12 : Tâche de classification de graphes

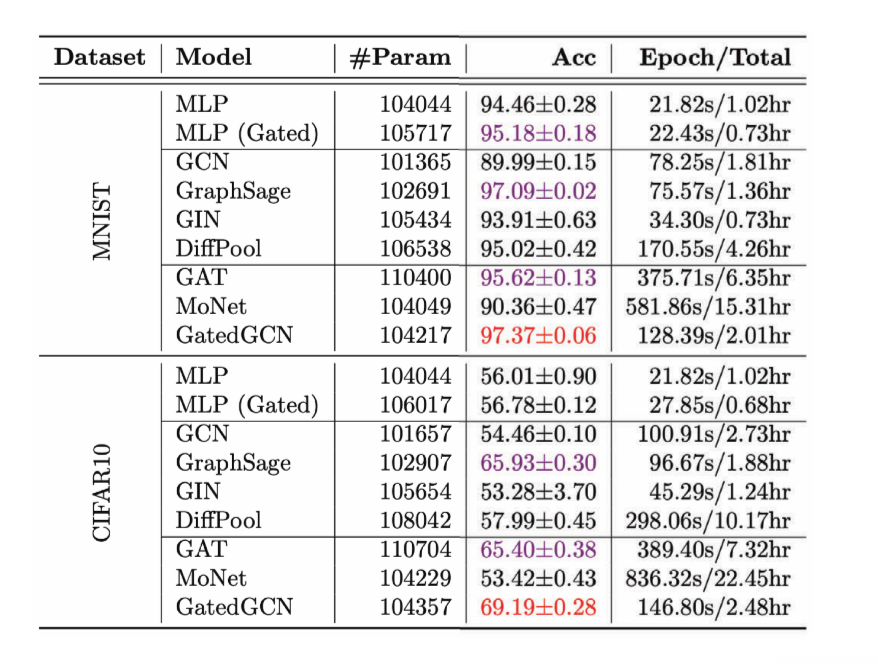
Figure 13 : Performance de divers GCNs sur la tâche de classification de graphes

Pour une tâche de classification des arêtes, nous avons considéré le problème d’optimisation combinatoire du problème du voyageur de commerce (TSP en anglais pour Travelling Salesman Problem). Nous voulons savoir si une arête particuliere appartient à la solution optimale. S’il fait partie de la solution, il appartient à la classe 1, sinon à la classe 0. Ici, nous avons besoin de caractéristiques explicites des arêtes et le seul modèle qui fait un bon travail à cet égard est GatedGCN.

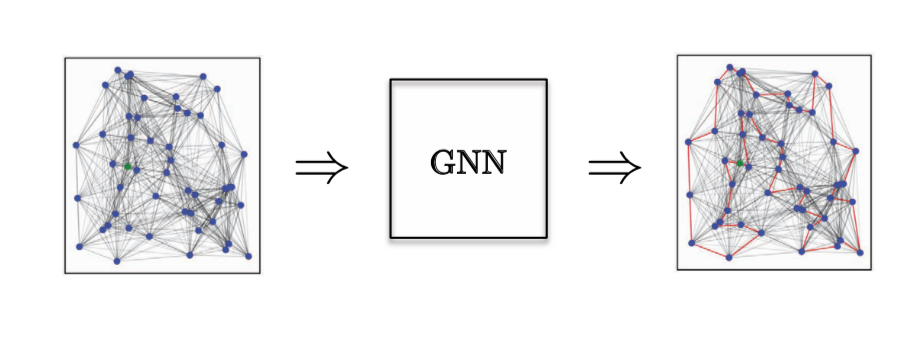
Figure 14 : Tâche de classification des arêtes

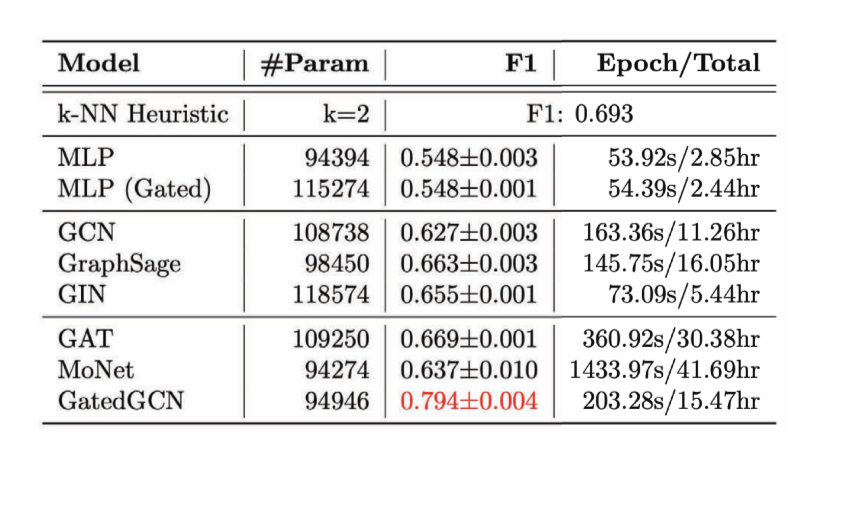
Figure 15 : Performance de divers GCNs sur la tâche de classification des arêtes

Les GCNs ne se limitent pas à des modèles d’apprentissage supervisés et peuvent être utilisés pour des tâches autosupervisées. Selon Yann, presque toutes les tâches d’apprentissage autosupervisé exploitent une sorte de structure graphique. Lorsque nous effectuons une tâche d’apprentissage autosupervisé dans un texte, nous prenons une séquence de mots et nous apprenons à prédire les mots manquants ou les nouvelles phrases. Il existe ici une structure graphique, qui correspond au nombre de fois qu’un mot apparaît à une certaine distance d’un autre mot. Le texte serait un graphe linéaire et les voisins choisis seraient utilisés pour entraîner un transformer. Dans le cas de l’entraînement contrastif, où nous avons deux échantillons qui sont similaires et deux qui sont dissemblables, il s’agit essentiellement d’un graphe de similarité où deux échantillons sont liés lorsqu’ils sont similaires et s’ils ne le sont pas, ils sont considérés comme dissemblables.

Conclusion

Les GCNs généralisent les ConvNets pour les données de type graphes. L’opérateur de convolution a dû être repensé. Cette opération a donné naissance aux GCNs spatiaux pour l’appariement de patrons et aux GCNs spectraux pour la convolution spectrale. Il existe une complexité linéaire pour les graphes épars et l’implémentation GPU, bien que cette dernière ne soit pas encore optimisée pour la multiplication des matrices éparses. Les applications sont nombreuses, comme le montre le tableau ci-dessous.

Figure 16 : Applications