Attention et Transformer

Attention

Nous introduisons le concept d’attention avant de parler de l’architecture du Transformer. Il existe deux types principaux d’attention : l’auto-attention vs l’attention croisée. Dans ces catégories, nous pouvons avoir une attention dure vs une attention douce.

Comme nous le verrons plus tard, les transformers sont constitués de modules d’attention, qui sont des associations entre des ensembles (plutôt que des séquences), ce qui signifie que nous n’imposons pas d’ordre à nos entrées/sorties.

Auto-attention (I)

Considérons un ensemble de $t$ d’entrée $\boldsymbol{x}$’s :

où chaque symbole $\boldsymbol{x}_i$ est un vecteur dimensionnel $n$. Comme l’ensemble comporte des éléments $t$, dont chacun appartient à $\mathbb{R}^n$, nous pouvons représenter l’ensemble comme une matrice $\boldsymbol{X}\in\mathbb{R}^{n \times t}$.

Avec l’auto-attention, la représentation cachée $h$ est une combinaison linéaire des entrées :

En utilisant la représentation matricielle décrite ci-dessus, nous pouvons écrire la couche cachée comme le produit matriciel :

où $\boldsymbol{a} \in \mathbb{R}^t$ est un vecteur colonne avec les composantes $\alpha_i$.

A noter que cela diffère de la représentation cachée que nous avons vue jusqu’à présent, où les entrées sont multipliées par une matrice de poids.

Selon les contraintes que nous imposons au vecteur $\vect{a}$, nous pouvons obtenir une attention dure ou douce.

Attention dure

Avec beaucoup d’attention, nous imposons aux alphas la contrainte suivante : $\Vert\vect{a}\Vert_0 = 1$. Cela signifie que $\vect{a}$ est un vecteur one-hot. Par conséquent, tous les coefficients de la combinaison linéaire des entrées sauf un sont égaux à $0$ et la représentation cachée se réduit à l’entrée $\boldsymbol{x}_i$ correspondant à l’élément $\alpha_i=1$.

Attention douce

Avec une attention douce, nous imposons que $\Vert\vect{a}\Vert_1 = 1$. La représentation cachée est une combinaison linéaire des entrées où les coefficients s’additionnent à 1.

Auto-attention (II)

D’où viennent les $\alpha_i$ ?

Nous obtenons le vecteur $\vect{a} \in \mathbb{R}^t$ de la manière suivante :

où $\beta$ représente le paramètre de température inverse du $\text{soft(arg)max}(\cdot)$. $\boldsymbol{X}^{\top}\in\mathbb{R}^{t \times n}$ est la représentation matricielle transposée de l’ensemble $\lbrace\boldsymbol{x}_i \rbrace_{i=1}^t$, et $\boldsymbol{x}$ représente un $\boldsymbol{x}_i$ générique de l’ensemble. Notez que la ligne $j$ème de $X^{\top}$ correspond à un élément $\boldsymbol{x}_j\in\mathbb{R}^n$, Ainsi, la $j$ème rangée de $\boldsymbol{X}^{\top}\boldsymbol{x}$ est le produit scalaire de $\boldsymbol{x}_j$ avec chaque $\boldsymbol{x}_i$ dans $\lbrace \boldsymbol{x}_i \rbrace_{i=1}^t$.

Les composantes du vecteur $\vect{a}$ sont également appelées scores car le produit scalaire entre deux vecteurs nous indique dans quelle mesure deux vecteurs sont alignés ou similaires. Par conséquent, les éléments de $\vect{a}$ fournissent des informations sur la similarité de l’ensemble global avec un symbole particulier $\boldsymbol{x}_i$.

Les crochets représentent un argument facultatif. A noter que si $\arg\max(\cdot)$ est utilisé, nous obtenons un vecteur one-hot d’alphas, ce qui entraîne une attention soutenue. En revanche, $\text{soft(arg)max}(\cdot)$ conduit à une attention douce. Dans chaque cas, les composantes du vecteur résultant $\vect{a}$ s’additionnent à 1.

En générant $\vect{a}$ de cette façon, on obtient un ensemble d’entre elles, une pour chaque symbole $\boldsymbol{x}_i$. De plus, chaque $\vect{a}_i \in \mathbb{R}^t$ permet d’empiler les alphas dans une matrice $\boldsymbol{A}\in \mathbb{R}^{t \times t}$.

Comme chaque état caché est une combinaison linéaire des entrées $\boldsymbol{X}$ et d’un vecteur $\vect{a}$, nous obtenons un ensemble d’états cachés $t$, que nous pouvons empiler dans une matrice $\boldsymbol{H}\in \mathbb{R}^{n \times t}$.

Key-value store

Un key-value store est un paradigme conçu pour le stockage (sauvegarde), la récupération (interrogation) et la gestion de tableaux associatifs (dictionnaires / tables de hachage).

Par exemple, disons que nous voulons trouver une recette pour faire des lasagnes. Nous avons un livre de recettes et nous cherchons « lasagne » : c’est la requête. Cette requête est comparée à toutes les clés possibles de votre ensemble de données : dans ce cas, il peut s’agir des titres de toutes les recettes du livre. Nous vérifions l’alignement de la requête avec chaque titre pour trouver le score maximum de correspondance entre la requête et toutes les clés respectives. Si notre résultat est la fonction argmax, nous récupérons la recette unique ayant obtenu le score le plus élevé. Sinon, si nous utilisons une fonction argmax souple, nous obtenons une distribution de probabilité et pouvons récupérer dans l’ordre, à partir du contenu le plus similaire, les recettes de moins en moins pertinentes qui correspondent à la requête.

Fondamentalement, la requête est la question. Pour une même question, nous comparons cette requête à chaque clé et nous récupérons tout le contenu correspondant.

Requêtes (q), clés (k) et valeurs (v)

Chacun des vecteurs $\vect{q}, \vect{k}, \vect{v}$ peut être simplement considéré comme une rotation de l’entrée spécifique $\vect{x}$. Où $\vect{q}$ est juste $\vect{x}$ tourné par $\vect{W_q}$, $\vect{k}$ est juste $\vect{x}$ tourné par $\vect{W_k}$ et de même pour $\vect{v}$. Notons que c’est la première fois que nous introduisons des paramètres apprenables. Nous n’incluons pas non plus de non-linéarités puisque l’attention est entièrement basée sur l’orientation.

Afin de comparer la requête à toutes les clés possibles, $\vect{q}$ et $\vect{k}$ doivent avoir la même dimensionnalité, c’est-à-dire $\vect{q}, \vect{k} \in \mathbb{R}^{d’}$.

Cependant, $\vect{v}$ peut être de n’importe quelle dimension. Si nous continuons avec notre exemple de recette de lasagnes, nous avons besoin que la requête ait la dimension comme clés, c’est-à-dire les titres des différentes recettes que nous recherchons. La dimension de la recette correspondante $\vect{v}$, peut cependant être arbitrairement longue. Nous avons donc ce $\vect{v} \in \mathbb{R}^{d’’}$.

Par souci de simplicité, nous supposerons ici que tout est de dimension $d$, c’est-à-dire :

Nous avons donc maintenant un ensemble de $\vect{x}$, un ensemble de requêtes, un ensemble de clés et un ensemble de valeurs. Nous pouvons empiler ces ensembles dans des matrices dont chacune comporte des colonnes $t$ puisque nous avons empilé $t$ vecteurs. Chaque vecteur a une hauteur $d$.

Nous comparons une requête $\vect{q}$ à la matrice de toutes les clés $\vect{K}$ :

La couche cachée est alors la combinaison linéaire des colonnes de $\vect{V}$ pondérées par les coefficients $\vect{a}$ :

Puisque nous avons des requêtes $t$, nous obtenons $t$ correspondant aux $\vect{a}$ poids et donc une matrice $\vect{A}$ de dimension $t \times t$.

C’est pourquoi, en notation matricielle, nous avons :

A part, nous mettons généralement $\beta$ à :

Ceci est fait pour maintenir la température constante parmi les différents choix de dimension $d$ et nous divisons donc par la racine carrée du nombre de dimensions $d$.

Pour l’implémentation, nous pouvons accélérer le calcul en empilant tous les $\vect{W}$ en un seul grand $\vect{W}$ et calculer ensuite $\vect{q}, \vect{k}, \vect{v}$ en une seule fois :

Il y a aussi le concept de têtes. Nous avons vu ci-dessus un exemple avec une seule tête, mais nous pouvons en avoir plusieurs. Par exemple, disons que nous avons $h$ têtes puis nous avons des $h$ $\vect{q}$, $h$ $\vect{k}$ et $h$ $\vect{v}$ et nous nous retrouvons avec un vecteur en $\mathbb{R}^{3hd}$ :

Cependant, nous pouvons toujours transformer les valeurs des têtes pour obtenir la dimension originale $\R^d$ en utilisant un $\vect{W_h} \in \mathbb{R}^{d \times hd}$. Ce n’est qu’une des façons possibles de mettre en œuvre le key-value store.

Le Transformer

En élargissant notre connaissance de l’attention, nous interprétons maintenant les éléments fondamentaux du transformer. En particulier, nous allons faire une passe en avant à travers un transformer de base et voir comment l’attention est utilisée dans le paradigme standard de l’encodeur-décodeur. Nous allons également effectuer une comparaison avec les architectures séquentielles des RNNs.

Architecture encodeur-décodeur

Nous devons nous familiariser avec cette terminologie. Elle est surtout mise en évidence lors des démonstrations d’auto-encodeurs et constitue jusqu’à présent un préalable à la compréhension. Pour résumer, une entrée passe par un encodeur et un décodeur qui imposent une sorte de goulot d’étranglement aux données, ne laissant passer que les informations les plus importantes. Ces informations sont stockées dans la sortie du bloc de l’encodeur et peuvent être utilisées pour toute une série de tâches sans rapport les unes avec les autres.

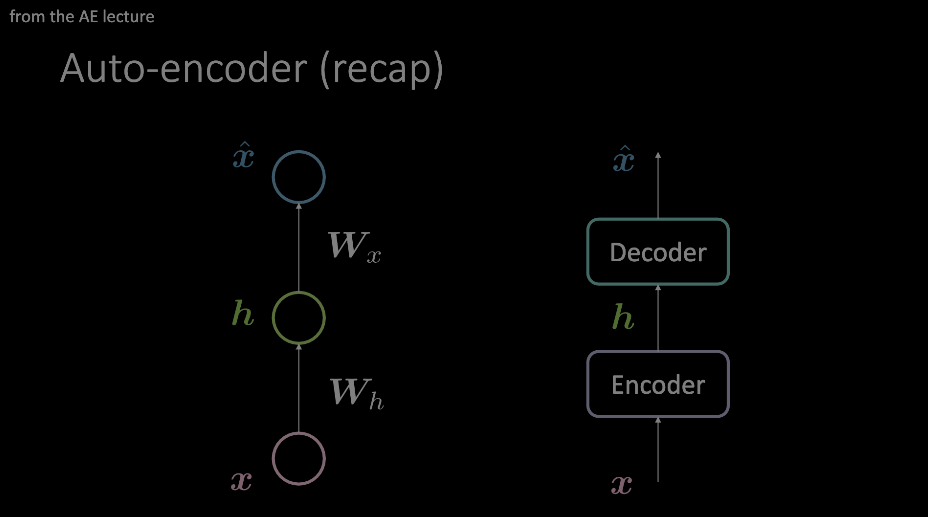
Figure 1 : Deux exemples de diagrammes d'un auto-encodeur. Le modèle de gauche montre comment un auto-encodeur peut être conçu avec deux transformations affines + activations. L'image de droite remplace cette couche unique par un module d'opérations arbitraire.

Notre attention est attirée sur la disposition de l’auto-encodeur comme indiqué dans le modèle de droite et nous allons maintenant jeter un coup d’œil à l’intérieur, dans le contexte des transformers.

Module Encodeur

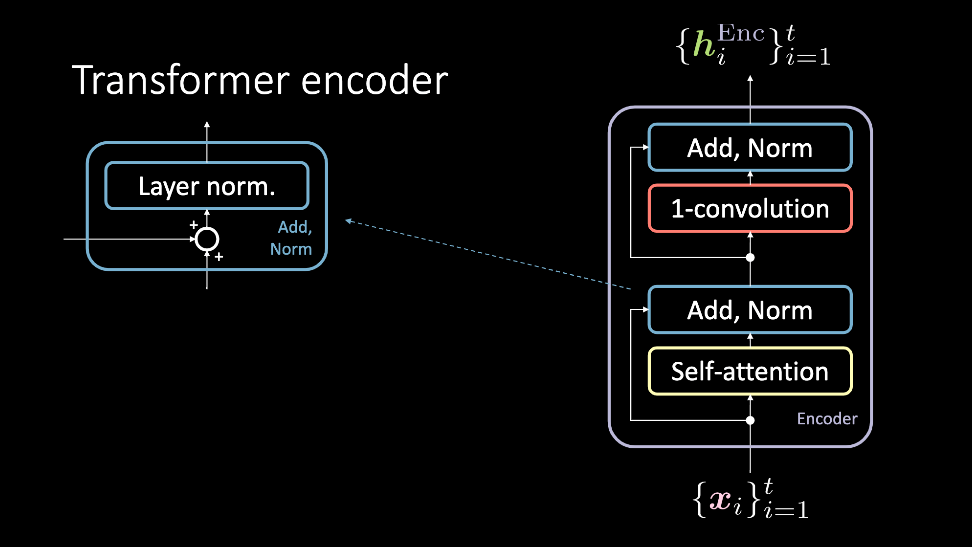
Figure 2 : L’encodeur du transformer prend un ensemble d'entrées $\vect{x}$ et renvoie un ensemble de représentations cachées $\vect{h}^\text{Enc}$

Le module d’encodage accepte un ensemble d’entrées, qui sont simultanément passées par le bloc d’auto-attention et le contourne pour atteindre le bloc Add, Norm. À ce stade, elles sont à nouveau passées simultanément par la convolution 1D et un autre bloc Add, Norm. Elles en ressortent en sortie comme l’ensemble de la représentation cachée. Cet ensemble de représentation cachée est alors envoyé soit par un nombre arbitraire de modules d’encodage (c’est-à-dire plus de couches), soit au décodeur. Nous allons examiner ces blocs plus en détail.

Auto-attention

Le modèle d’auto-attention est un modèle d’attention normale. La requête, la clé et la valeur sont générées à partir du même élément de l’entrée séquentielle. Dans les tâches qui tentent de modéliser des données séquentielles, des encodeurs de position sont ajoutés avant cette entrée. La sortie de ce bloc est constituée des valeurs pondérées de l’attention. Le bloc auto-attention accepte un ensemble d’entrées, de $1, \cdots, t$, et produit des valeurs pondérées par l’attention de $1, \cdots, t$ qui sont transmises au reste de l’encodeur.

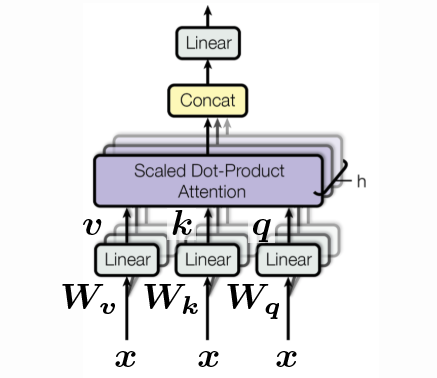
Figure 3 : Le bloc auto-attention. La séquence d'entrées est représentée comme un ensemble le long de la 3ème dimension et concaténée

Add, Norm

Le bloc Add&Norm a deux composantes. Le premier est le bloc Add, qui est une connexion résiduelle et le deuxième Norm qui est la normalisation des couches.

Convolution 1D

Après cette étape, une convolution 1D est appliquée. Ce bloc est constitué de deux couches denses. En fonction des valeurs définies, ce bloc permet d’ajuster les dimensions de la sortie $\vect{h}^\text{Enc}$.

Module décodeur

Le transformer-décodeur suit une procédure similaire à celle de l’encodeur. Cependant, il y a un sous-bloc supplémentaire à prendre en compte. De plus, les entrées de ce module sont différentes.

Figure 4 : Une explication plus amicale du décodeur

Attention croisée

L’attention croisée suit la configuration des requêtes, des clés et des valeurs utilisées pour les blocs d’auto-attention. Cependant, les entrées sont un peu plus compliquées. L’entrée dans le décodeur est un point de données $\vect{y}_i$, qui est ensuite passé par l’auto-attention et les blocs Add Norm, et qui se termine finalement par le bloc d’auto-attention. Celui-ci sert de requête pour l’attention croisée, où les paires de clés et de valeurs sont la sortie $\vect{h}^\text{Enc}$, où cette sortie a été calculée avec toutes les entrées passées $\vect{x}_1, \cdots, \vect{x}_{t}$.

Résumé

Un ensemble, $\vect{x}_1$ à $\vect{x}_{t}$ est transmis par l’encodeur. En utilisant l’auto-attention et quelques autres blocs, on obtient une représentation de sortie, $\lbrace\vect{h}^\text{Enc}\rbrace_{i=1}^t$, qui est envoyée au décodeur. Après lui avoir appliqué l’auto-attention, l’attention croisée est appliquée. Dans ce bloc, la requête correspond à une représentation d’un symbole dans la langue cible $\vect{y}_i$, et la clé et les valeurs proviennent de la phrase de la langue source ($\vect{x}_1$ à $\vect{x}_{t}$). Intuitivement, l’attention croisée permet de trouver quelles valeurs de la séquence d’entrée sont les plus pertinentes pour construire $\vect{y}_t$, et méritent donc les coefficients d’attention les plus élevés. La sortie de cette attention croisée est ensuite acheminée à travers un autre sous-bloc à convolution 1D et nous obtenons $\vect{h}^\text{Dec}$. Pour la langue cible spécifiée, il est facile de voir comment l’entraînement va commencer, en comparant $\lbrace\vect{h}^\text{Dec}\rbrace_{i=1}^t$ à certaines données cibles.

Modèles du monde en linguistique

Abordons quelques éléments laissés de côté lors de l’explication des modules les plus importants d’un transformer pour comprendre comment cette architecture peut obtenir des résultats de pointe dans les tâches linguistiques.

L’encodage positionnel

Les mécanismes d’attention nous permettent de mettre en parallèle les opérations et d’accélérer considérablement le temps d’entraînement d’un modèle mais perdent des informations séquentielles. L’encodage positionnel nous permet de saisir ce contexte.

Représentations sémantiques

Tout au long de l’entraînement d’un transformer, de nombreuses représentations cachées sont générées. Pour créer un espace d’enchâssement similaire à celui utilisé dans PyTorch, la sortie de l’attention croisée fournit une représentation sémantique du mot $x_i$ pouvant servir à d’autres expériences (tâches) sur ce jeu de données.

Résumé du code

Voyons les blocs du transformer dont nous avons parlé plus haut dans un format beaucoup plus compréhensible : le code !

Dans le premier module, nous examinons le bloc d’attention mullti-têtes. En fonction de la requête, de la clé et des valeurs entrées dans ce bloc, il peut être utilisé pour l’auto-attention ou l’attention croisée.

class MultiHeadAttention(nn.Module):
    def __init__(self, d_model, num_heads, p, d_input=None):
        super().__init__()
        self.num_heads = num_heads
        self.d_model = d_model
        if d_input is None:
            d_xq = d_xk = d_xv = d_model
        else:
            d_xq, d_xk, d_xv = d_input
        # L'enchâssement de la dimension du modele est un multiple du nombre de têtes
        assert d_model % self.num_heads == 0
        self.d_k = d_model // self.num_heads
        # Ceux-ci sont toujours de dimension d_model. Pour diviser en nombre de têtes
        self.W_q = nn.Linear(d_xq, d_model, bias=False)
        self.W_k = nn.Linear(d_xk, d_model, bias=False)
        self.W_v = nn.Linear(d_xv, d_model, bias=False)
        # Les sorties de toutes les sous-couches doivent être de dimension d_model.
        self.W_h = nn.Linear(d_model, d_model)

Initialisation de la classe d’attention à plusieurs têtes. Si une d_input est fournie, cela devient une attention croisée. Sinon, c’est l’auto-attention. La configuration de la requête, de la clé, de la valeur est construite comme une transformation linéaire du d_model d’entrée.

def scaled_dot_product_attention(self, Q, K, V):
    batch_size = Q.size(0)
    k_length = K.size(-2)

     Mise à l'échelle par d_k pour que le soft(arg)max ne sature pas
    Q = Q / np.sqrt(self.d_k)  # (bs, n_heads, q_length, dim_per_head)
    scores = torch.matmul(Q, K.transpose(2,3))  # (bs, n_heads, q_length, k_length)

    A = nn_Softargmax(dim=-1)(scores)  # (bs, n_heads, q_length, k_length)

    # Donne la moyenne pondérée des valeurs
    H = torch.matmul(A, V)  # (bs, n_heads, q_length, dim_per_head)

    return H, A

Retourne la couche cachée correspondant aux encodeurs des valeurs après mise à l’échelle par le vecteur d’attention. Pour des raisons comptables (quelles valeurs de la séquence ont été masquées par l’attention ?), $A$ est également renvoyé.

def split_heads(self, x, batch_size):
    return x.view(batch_size, -1, self.num_heads, self.d_k).transpose(1, 2)

Divise la dernière dimension en (heads × depth). On renvoie après transposition pour mettre en forme (batch_size × num_heads × seq_length × d_k)

def group_heads(self, x, batch_size):
    return x.transpose(1, 2).contiguous().
        view(batch_size, -1, self.num_heads * self.d_k)

Combine les têtes d’attention ensemble, pour obtenir une forme correcte conforme à la taille du batch et à la longueur de la séquence.

def forward(self, X_q, X_k, X_v):
    batch_size, seq_length, dim = X_q.size()
    # Après la transformation, divise en num_heads
    Q = self.split_heads(self.W_q(X_q), batch_size)
    K = self.split_heads(self.W_k(X_k), batch_size)
    V = self.split_heads(self.W_v(X_v), batch_size)
    # Calcule les poids d'attention pour chacune des têtes
    H_cat, A = self.scaled_dot_product_attention(Q, K, V)
    # Remettre toutes les têtes ensemble par concaténation
    H_cat = self.group_heads(H_cat, batch_size)  # (bs, q_length, dim)
    # Couche linéaire finale
    H = self.W_h(H_cat)  # (bs, q_length, dim)
    return H, A

Le passage en avant de l’attention à plusieurs têtes.

Une entrée donnée est divisée en q, k et v, et ces valeurs sont alors transmises par un mécanisme d’attention par produit scalaire, puis concaténées et transmises par une couche linéaire finale. La dernière sortie du bloc d’attention est l’attention trouvée et la représentation cachée qui est passée à travers les blocs restants.

Le bloc Add,Norm est une fonction déjà intégrée dans PyTorch. En tant que telle, c’est une implémentation extrêmement simple et n’a pas besoin de sa propre classe. Le bloc suivant est le bloc de convolution 1D.

Maintenant que toutes nos classes principales sont construites (ou construites pour nous), nous nous tournons vers un module encodeur.

class EncoderLayer(nn.Module):
    def __init__(self, d_model, num_heads, conv_hidden_dim, p=0.1):
        self.mha = MultiHeadAttention(d_model, num_heads, p)
        self.layernorm1 = nn.LayerNorm(normalized_shape=d_model, eps=1e-6)
        self.layernorm2 = nn.LayerNorm(normalized_shape=d_model, eps=1e-6)

    def forward(self, x):
        attn_output, _ = self.mha(x, x, x)
        out1 = self.layernorm1(x + attn_output)
        cnn_output = self.cnn(out1)
        out2 = self.layernorm2(out1 + cnn_output)
        return out2

Dans les transformers les plus puissants, un nombre important de ces encodeurs sont empilés les uns sur les autres.

Rappelons que l’auto-attention n’a en soi ni récurrence ni convolutions, mais que c’est ce qui lui permet de fonctionner si rapidement. Pour être sensible à la position, nous fournissons des encodeurs de position. Ceux-ci sont calculés comme suit :

Pour ne pas trop s’attarder sur les détails, nous vous renvoyons au notebook pour le code complet utilisé. Il est disponible en anglais ici et en français ici.

Un encodeur complet, avec $N$ couches d’encodeur empilées, ainsi que des enchâssements de position, s’écrit :

class Encoder(nn.Module):
    def __init__(self, num_layers, d_model, num_heads, ff_hidden_dim,
            input_vocab_size, maximum_position_encoding, p=0.1):
        self.embedding = Embeddings(d_model, input_vocab_size,
                                    maximum_position_encoding, p)
        self.enc_layers = nn.ModuleList()
        for _ in range(num_layers):
            self.enc_layers.append(EncoderLayer(d_model, num_heads,
                                                ff_hidden_dim, p))
    def forward(self, x):
        x = self.embedding(x) # Transforme en (batch_size, input_seq_length, d_model)
        for i in range(self.num_layers):
            x = self.enc_layers[i](x)
        return x  # (batch_size, input_seq_len, d_model)

Exemple d’utilisation

Il y a beaucoup de tâches pour lesquelles vous pouvez utiliser un simple encodeur. Dans le notebook, nous voyons comment un encodeur peut être utilisé pour l’analyse des sentiments.

En utilisant le jeu de données d’IMDB (l’équivalent anglophone d’AlloCiné), nous pouvons sortir de l’encodeur une représentation latente d’une séquence de texte et entraîner ce processus d’encodage avec une entropie croisée binaire, correspondant à une critique de film positive ou négative. Là encore, nous laissons de côté les dessous techniques et nous vous dirigeons vers le notebook. Voici les composants architecturaux les plus importants utilisés dans le transformer :

class TransformerClassifier(nn.Module):
    def forward(self, x):
        x = Encoder()(x)
        x = nn.Linear(d_model, num_answers)(x)
        return torch.max(x, dim=1)

model = TransformerClassifier(num_layers=1, d_model=32, num_heads=2,
                         conv_hidden_dim=128, input_vocab_size=50002, num_answers=2)

Où ce modèle est entraîné de façon typique.