Le Truck Backer-Upper

Configuration

Le but est de construire un contrôleur autosupervisé qui contrôle la direction du camion pendant qu’il recule vers le quai de chargement à partir de n’importe quelle position initiale arbitraire.

A noter que seul le recul est autorisé, comme le montre la figure 1 ci-dessous.

Figure 1 : Le camion, la remorque et le quai de chargement

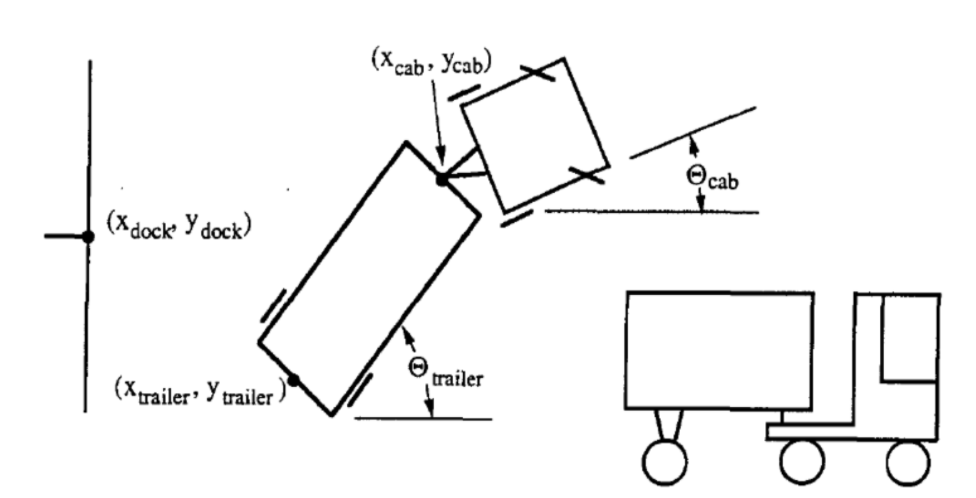L’état du camion est représenté par six paramètres :

• $\tcab$ : angle du camion
• $\xcab, \ycab$ : le cartésien de l’avant de la remorque.
• $\ttrailer$ : angle de la remorque
• $\xtrailer, \ytrailer$ : le cartésien de l’arrière de la remorque.

Le but du contrôleur est de sélectionner un angle approprié $\phi$ à chaque temps $k$, où après le camion reculera sur une petite distance fixe. Le succès dépend de deux critères :

1. L’arrière de la remorque est parallèle au quai de chargement mural, par exemple $\ttrailer = 0$.
2. L’arrière de la remorque ($\xtrailer, \ytrailer$) est aussi proche que possible du point ($x_{dock}, y_{dock}$) indiqué ci-dessus.

Plus de paramètres et de visualisation

Figure 2 : Paramètres de visualisation

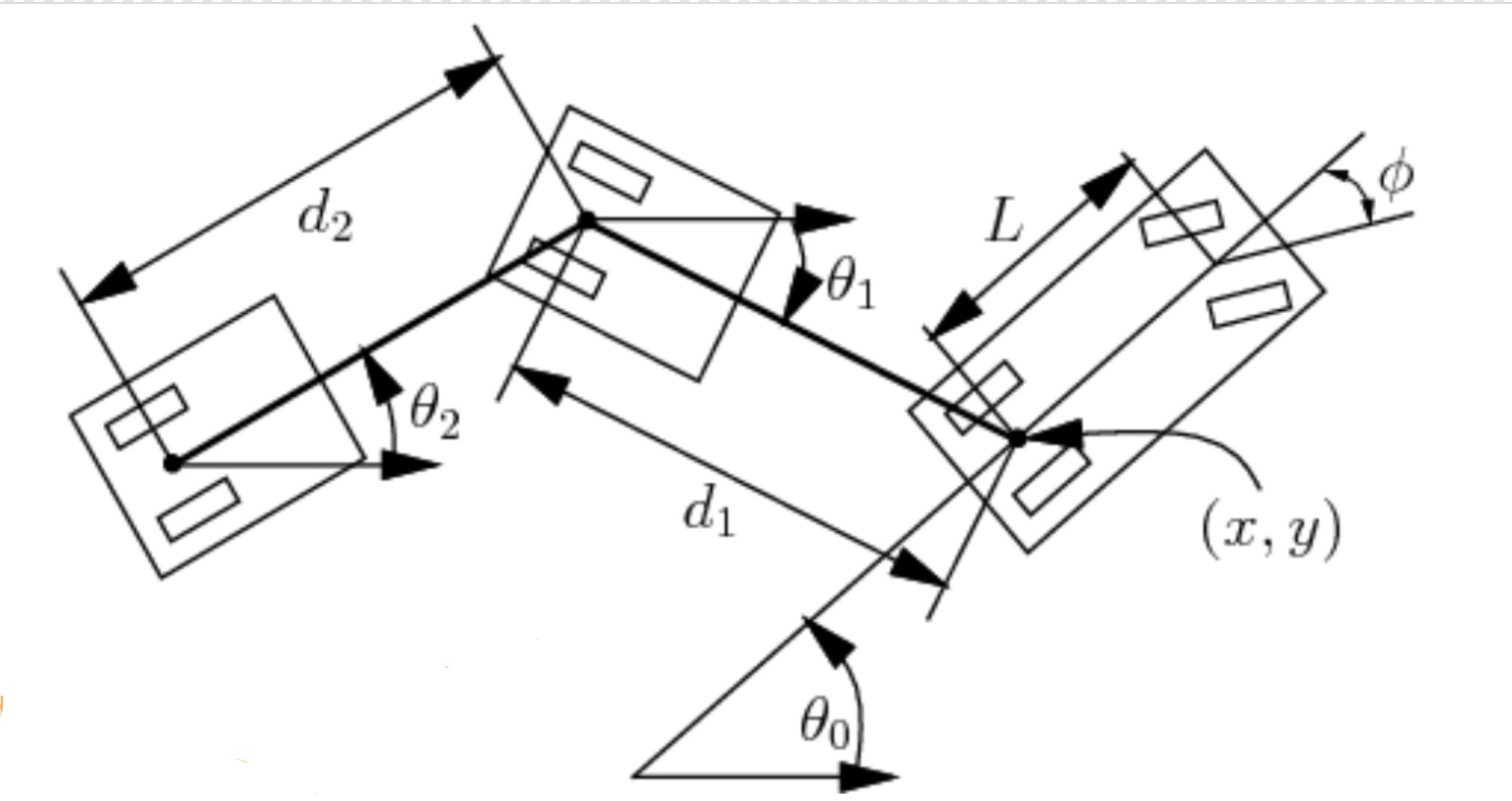Dans cette section, nous examinons quelques autres paramètres illustrés dans la figure 2. Étant donné la longueur de la voiture $L$, $d_1$ la distance entre la voiture et la remorque et $d_2$ la longueur de la remorque, nous pouvons calculer le changement d’angle et de positions :

Ici, $s$ indique la vitesse signée et $\phi$ l’angle de braquage négatif. Maintenant, nous pouvons représenter l’état par seulement quatre paramètres : $\xcab$, $\ycab$, $\theta_0$ et $\theta_1$. Cela s’explique par le fait que les paramètres de longueur sont connus et que $\xtrailer, \ytrailer$ est déterminé par $\xcab, \ycab, d_1, \theta_1$.

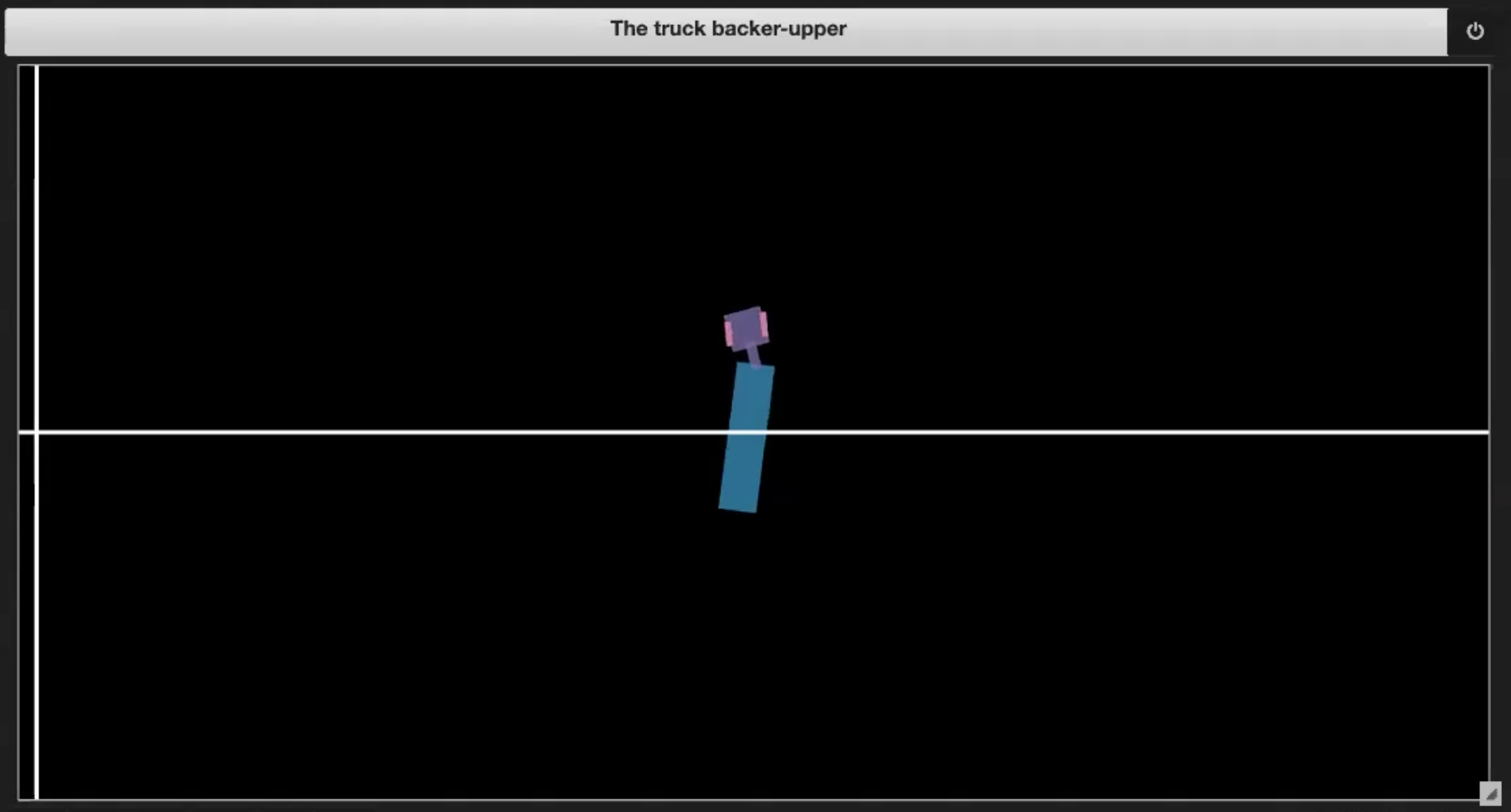
Les exemples d’environnements illustrés dans les figures 3 (1-4) peuvent être obtenus en exécutant le notebook Jupyter dont la version anglaise est disponible ici et la française ici :

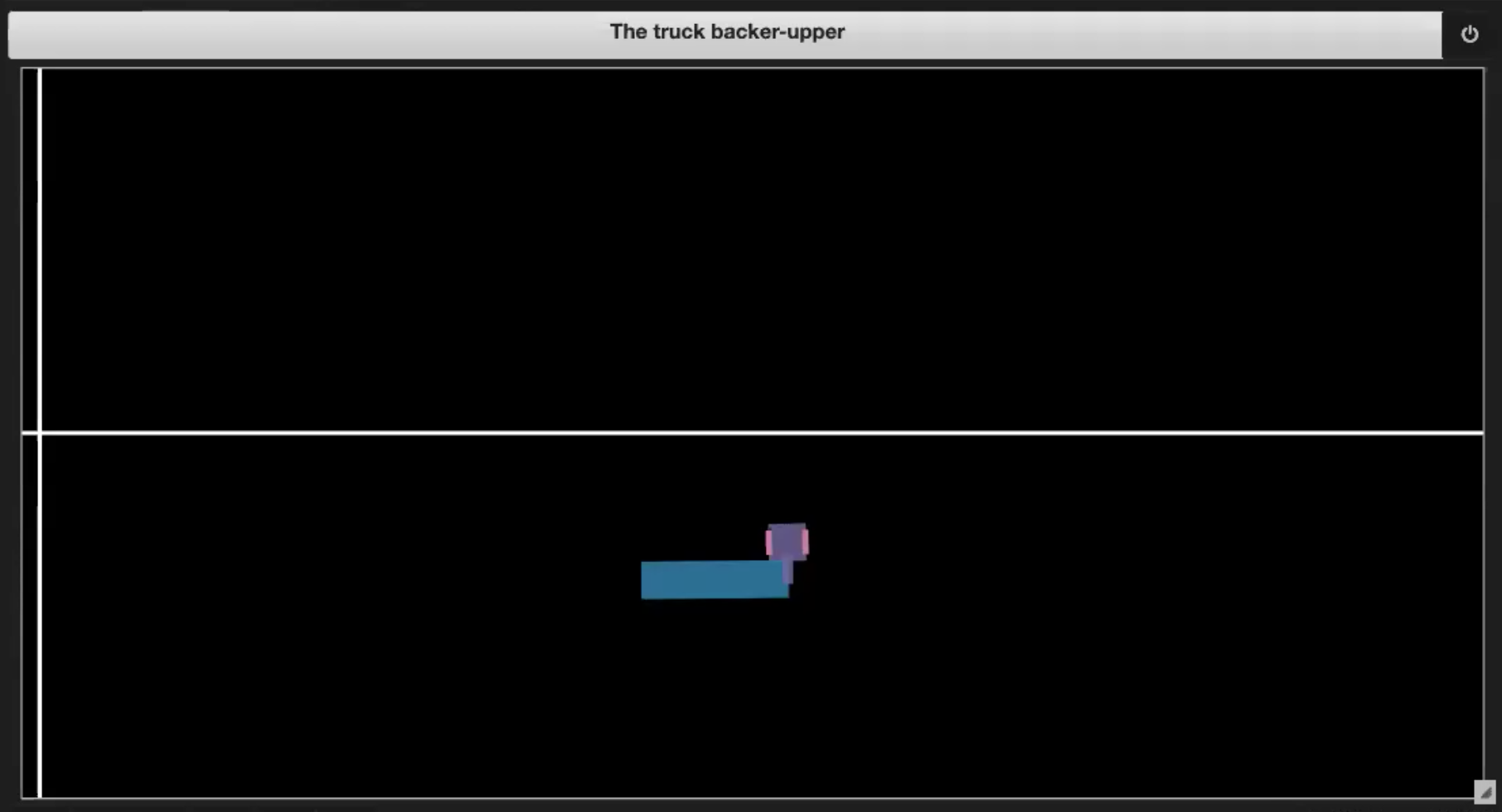
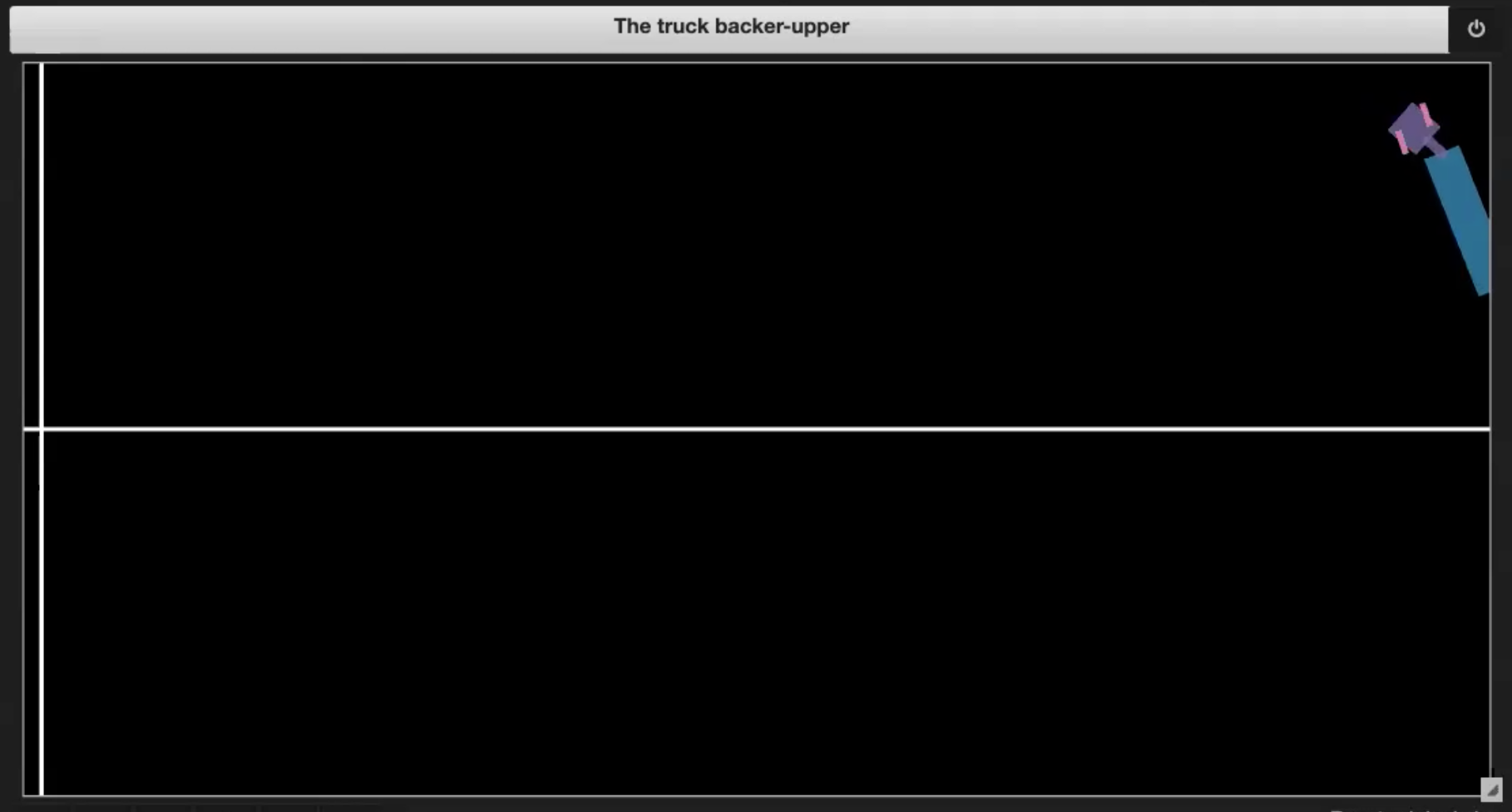
Figure 3.1 : Représentation de l’environnement	Figure 3.2 : Mise en portefeuille
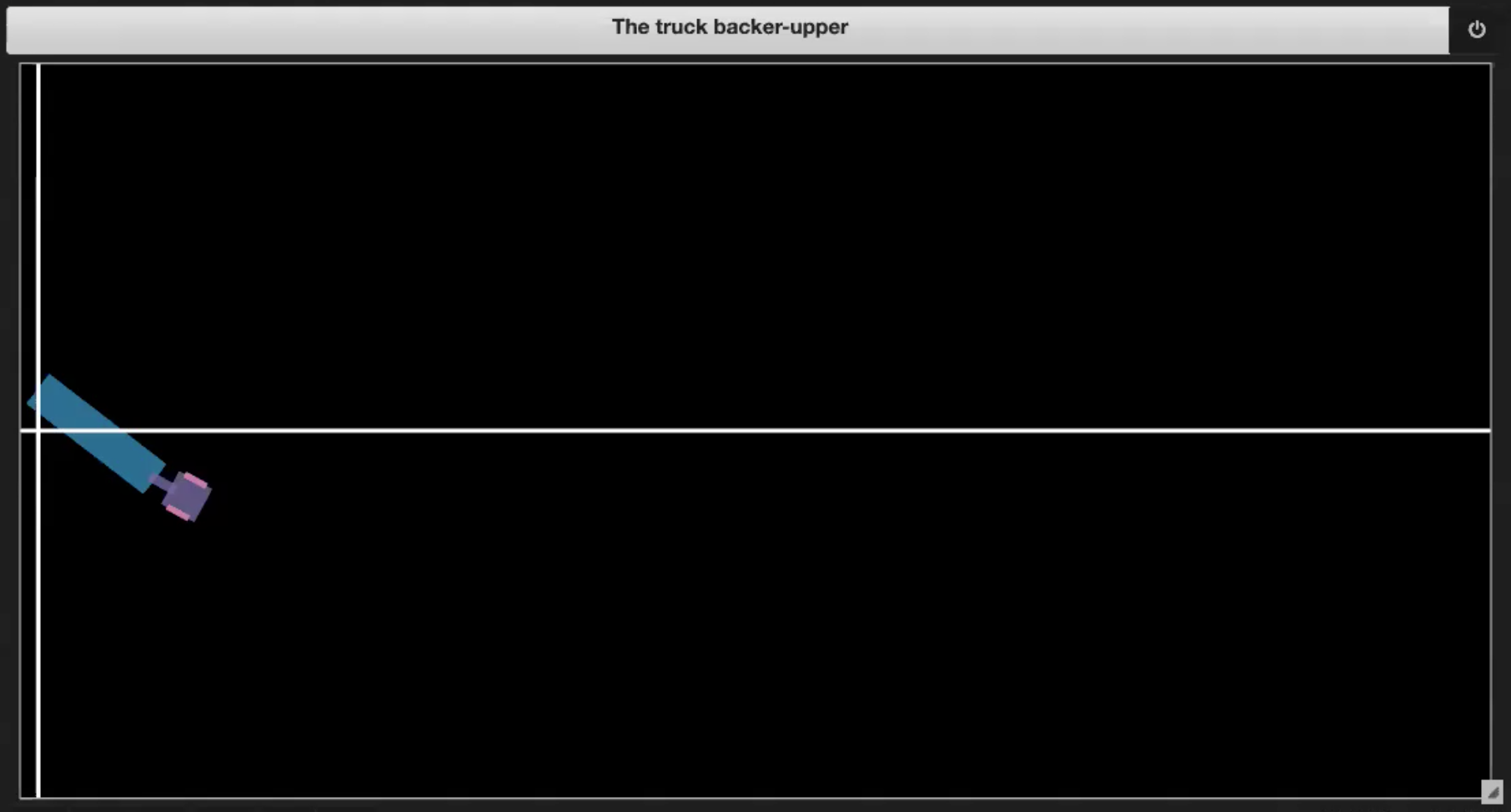Figure 3.3 : Sortie du cadre	Figure 3.4 : Atteindre le quai

À chaque pas de temps $k$, un signal de direction allant de $-\frac{\pi}{4}$ à $\frac{\pi}{4}$ est introduit et le camion reprend la route en utilisant l’angle correspondant.

Il existe plusieurs situations dans lesquelles la séquence peut se terminer :

• Si le camion se rentre dedans (mise en portefeuille, comme dans la figure 3.2)
• Si le camion sort de la limite (comme dans la figure 3.3)
• Si le camion atteint le quai (comme sur la figure 3.4)

Entraînement

Le processus d’entraînement comporte deux étapes :

• entraînement d’un réseau de neurones pour devenir un émulateur de la cinématique du camion et de la remorque
• entraînement d’un réseau de neurones pour contrôler le camion

Figure 4 : Diagramme général

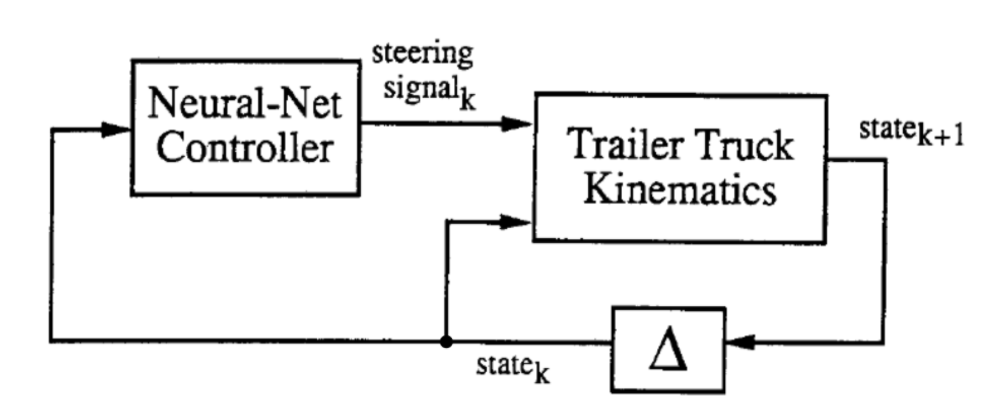Comme indiqué ci-dessus, dans le diagramme abstrait, les deux blocs sont les deux réseaux qui seront formés. À chaque pas de temps $k$, la cinématique du camion-remorque (ce que nous avons appelé émulateur), prend en compte le vecteur d’état en 6 dimensions et le signal de direction généré par le contrôleur et génère un nouvel état en 6 dimensions au temps $k + 1$.

Emulateur

L’émulateur prend l’emplacement actuel ($\tcab^t$,$\xcab^t, \ycab^t$, $\ttrailer^t$, $\xtrailer^t$, $\ytrailer^t$) plus le sens de direction $\phi^t$ comme entrée et sort l’état au pas de temps suivant ($\tcab^{t+1}$,$\xcab^{t+1}, \ycab^{t+1}$, $\ttrailer^{t+1}$, $\xtrailer^{t+1}$, $\ytrailer^{t+1}$). Il se compose d’une couche cachée linéaire, avec fonction d’activation ReLU, et d’une couche de sortie linéaire. Nous utilisons la MSE comme fonction de perte et entraînons l’émulateur via une descente de gradient stochastique.

Figure 5 : Entraînement de l'émulateur du réseau neuronal

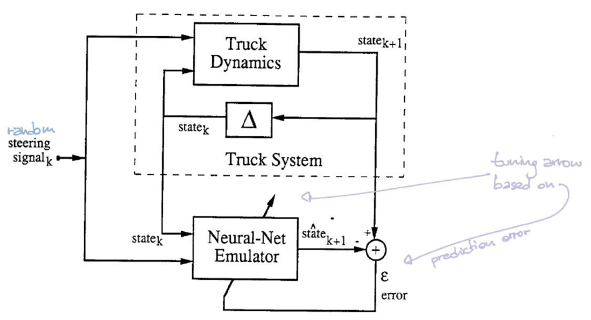Dans cette configuration, le simulateur peut nous indiquer l’emplacement de l’étape suivante, compte tenu de la position actuelle et de l’angle de braquage. Par conséquent, nous n’avons pas vraiment besoin d’un réseau neuronal qui émule le simulateur. Cependant, dans un système plus complexe, nous pouvons ne pas avoir accès aux équations sous-jacentes du système, c’est-à-dire que nous n’avons pas les lois de l’univers sous une forme calculable agréable. Nous ne pouvons observer que des données qui enregistrent des séquences de signaux de direction et leurs trajectoires correspondantes. Dans ce cas, nous voulons entraîner un réseau de neurones pour émuler la dynamique de ce système complexe.

Afin d’entraîner l’énumérateur, il y a deux fonctions importantes dans le Class truck que nous devons examiner lorsque nous formons l’émulateur.

La première est la fonction step qui donne l’état de sortie du camion après le calcul.

def step(self, ϕ=0, dt=1):

    # Vérifictions des conditions
    if self.is_jackknifed():
        print("Le camion s'est mis en portefeuille !")
        return

    if self.is_offscreen():
        print("Véhicule hors de l'écran")
        return

    self.ϕ = ϕ
    x, y, W, L, d, s, θ0, θ1, ϕ = self._get_atributes()

    # Effectuer une mise à jour de l'état
    self.x += s * cos(θ0) * dt
    self.y += s * sin(θ0) * dt
    self.θ0 += s / L * tan(ϕ) * dt
    self.θ1 += s / d * sin(θ0 - θ1) * dt

La seconde est la fonction state qui donne l’état actuel du camion.

def state(self):
        return (self.x, self.y, self.θ0, *self._traler_xy(), self.θ1)

Nous générons d’abord deux listes

• une liste d’entrée en ajoutant l’angle de braquage généré aléatoirement ϕ et l’état initial qui provient du camion en exécutant truck.state()
• une liste de sortie à laquelle est ajouté l’état de sortie du camion qui peut être calculé par truck.step(ϕ).

Nous pouvons maintenant entraîner l’émulateur :

cnt = 0
for i in torch.randperm(len(train_inputs)):
    ϕ_state = train_inputs[i]
    next_state_prediction = emulator(ϕ_state)

    next_state = train_outputs[i]
    loss = criterion(next_state_prediction, next_state)

    optimiser_e.zero_grad()
    loss.backward()
    optimiser_e.step()

    if cnt == 0 or (cnt + 1) % 1000 == 0:
        print(f'{cnt + 1:4d} / {len(train_inputs)}, {loss.item():.10f}')
    cnt += 1

Remarquons que torch.randperm(len(train_inputs)) nous donne une permutation aléatoire des indices dans la fourchette $0$ à la longueur des entrées d’entrainement moins $1$. Après la permutation des indices, chaque fois que ϕ_state est choisi dans la liste des entrées à l’index i. Nous entrons ϕ_state par la fonction de l’émulateur qui a une couche de sortie linéaire et nous obtenons next_state_prediction.
L’émulateur est un réseau de neurones défini comme ci-dessous :

emulator = nn.Sequential(
    nn.Linear(steering_size + state_size, hidden_units_e),
    nn.ReLU(),
    nn.Linear(hidden_units_e, state_size)
)

Ici, nous utilisons la MSE pour calculer la perte entre le véritable état suivant et la prédiction de l’état suivant, où le véritable état suivant provient de la liste de sortie avec l’indice i qui correspond à l’indice de l’état ϕ_state de la liste d’entrée.

Contrôleur

Le bloc $\matr{C}$ représente le contrôleur. Il prend en compte l’état actuel et fournit un angle de braquage. Ensuite, le bloc $\matr{T}$ (émulateur) prend à la fois l’état et l’angle pour produire l’état suivant.

Figure 6 : Diagramme de transition d'état

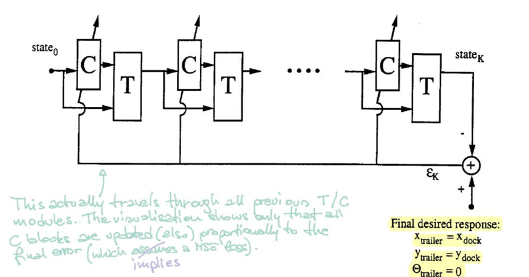Pour entraîner le contrôleur, nous partons d’un état initial aléatoire et répétons la procédure ($\matr{C}$ et $\matr{T}$) jusqu’à ce que la remorque soit parallèle au quai. L’erreur est calculée en comparant l’emplacement de la remorque et l’emplacement du quai. Nous trouvons ensuite les gradients en utilisant la rétropropagation et mettons à jour les paramètres du contrôleur via SGD.

Structure détaillée du modèle

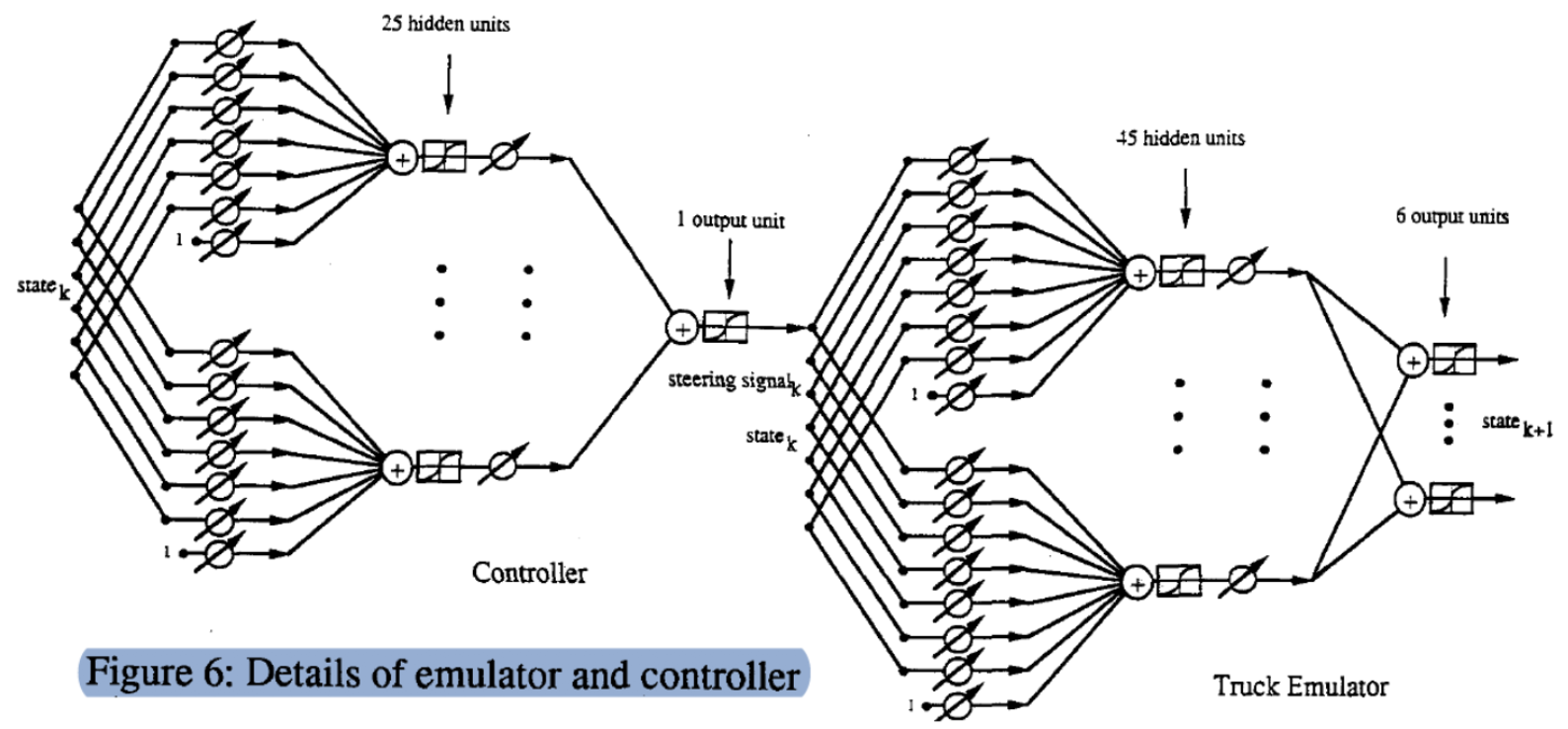
Voici un graphique détaillé du processus ($\matr{C}$, $\matr{T}$). Nous commençons par un état (vecteur à $6$ dimensions), le multiplions par une matrice de poids accordables et obtenons $25$ unités cachées. Ensuite, nous le faisons passer par un autre vecteur de poids accordables pour obtenir la sortie (signal de direction). De même, nous introduisons l’état et l’angle $\phi$ (vecteur à $7$ dimensions) à travers deux couches pour produire l’état de l’étape suivante.

Figure 7 : Détails de l'émulateur et du contrôleur

Pour y voir plus clair, nous montrons l’implémentation exacte de l’émulateur :

state_size = 6
steering_size = 1
hidden_units_e = 45

emulator = nn.Sequential(
    nn.Linear(steering_size + state_size, hidden_units_e),
    nn.ReLU(),
    nn.Linear(hidden_units_e, state_size)
)

optimiser_e = SGD(emulator.parameters(), lr=0.005)
criterion = nn.MSELoss()

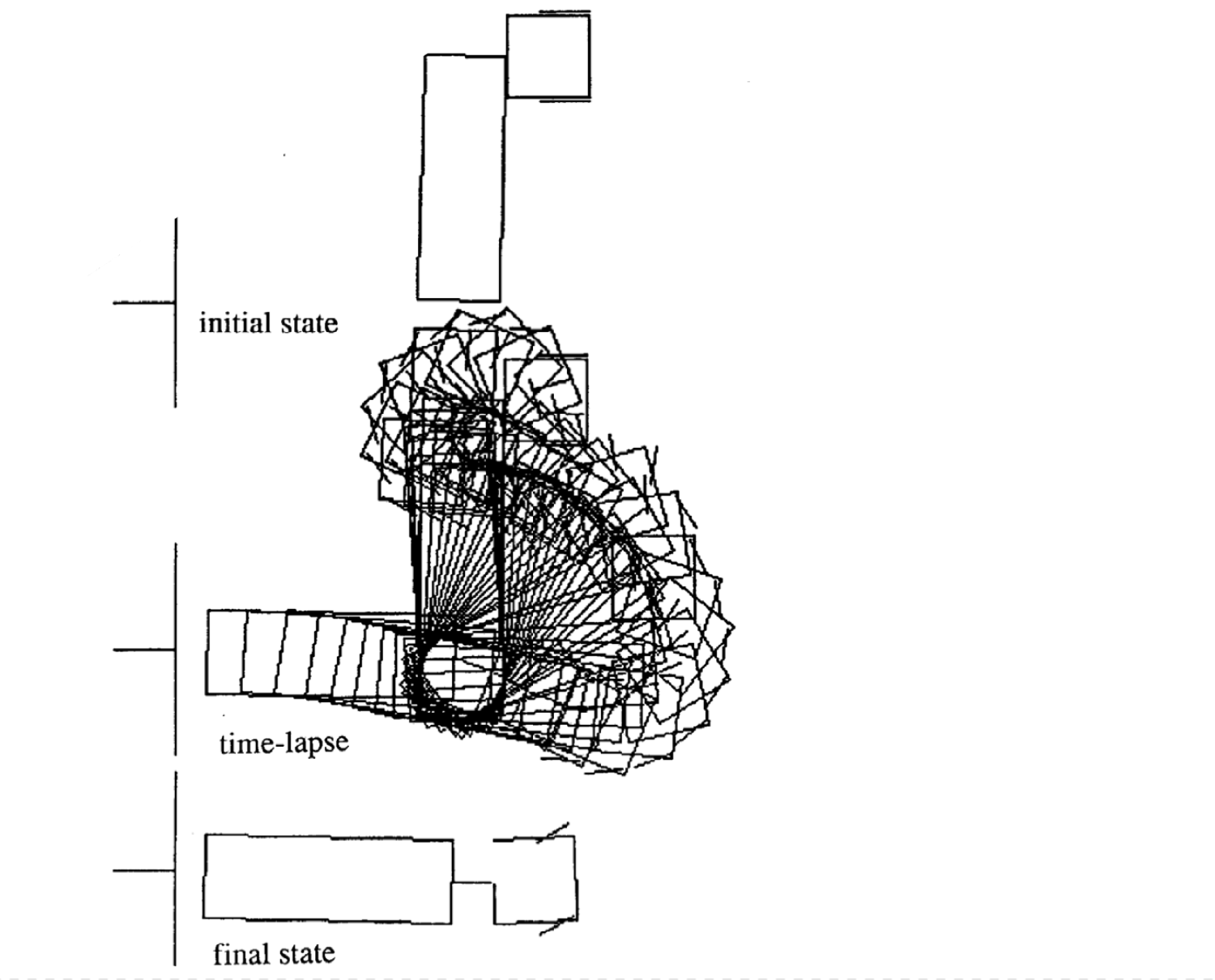
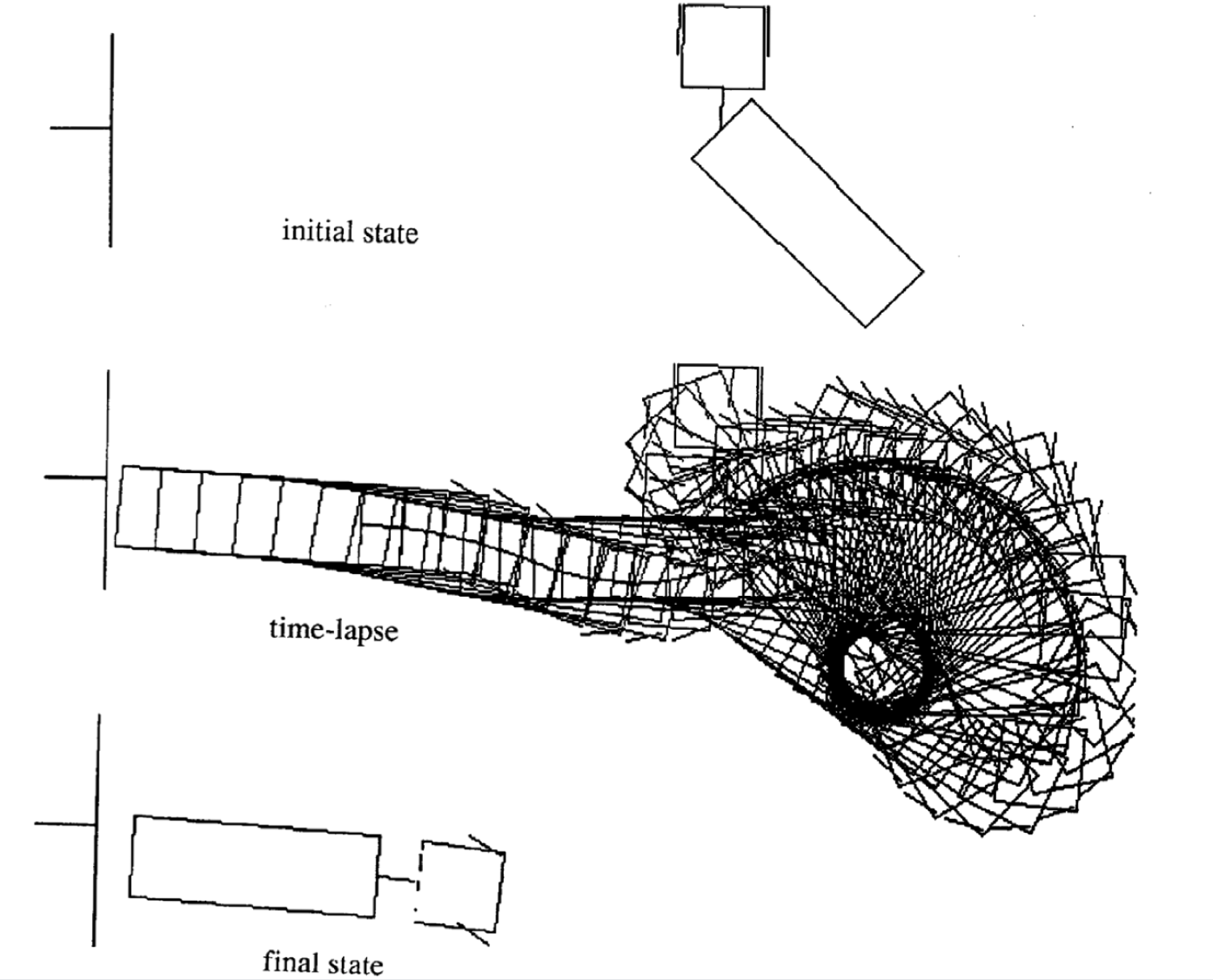
Exemples de mouvements

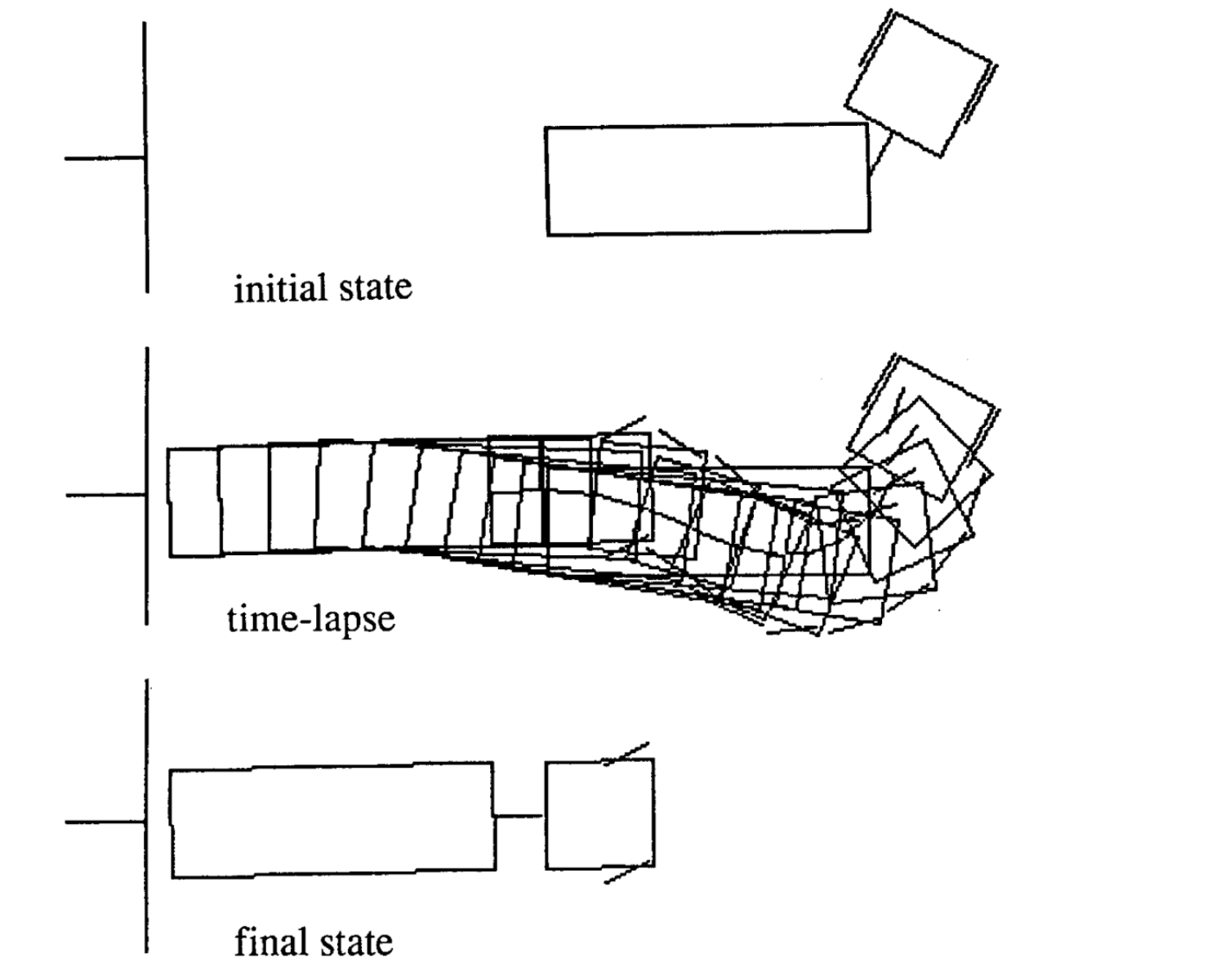
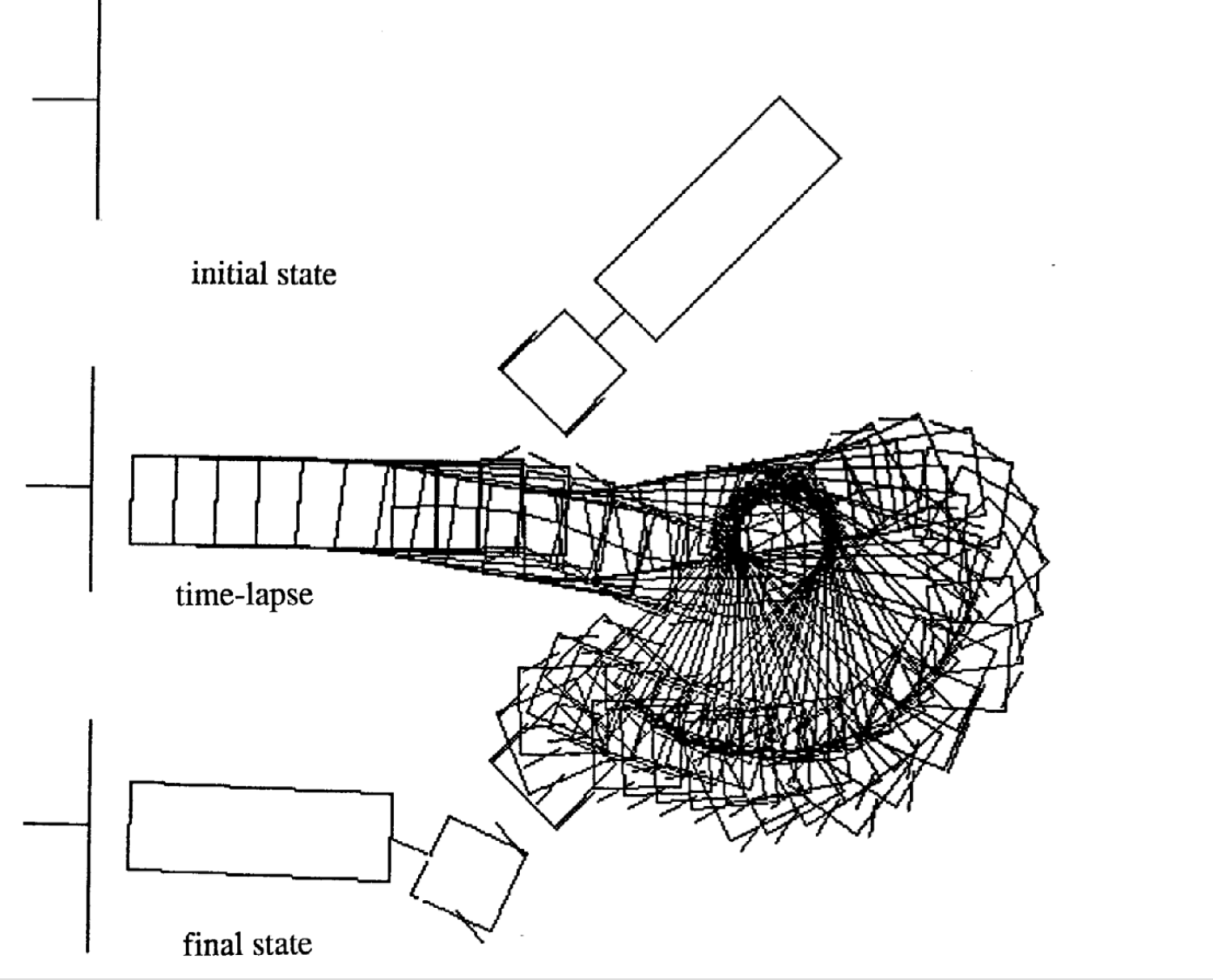
Voici quatre exemples de mouvements pour différents états initiaux. A noter que le nombre de pas de temps dans chaque épisode varie.

Figure 8 : Exemples de mouvements pour quatre états initiaux différents

Ressources supplémentaires :

Une démonstration complète est disponible à l’adresse suivante https://tifu.github.io/truck_backer_upper/. Il est aussi possible de consulter le code qui se trouve à l’adresse suivante : https://github.com/Tifu/truck_backer_upper.