Réseaux génératifs antagonistes

Introduction aux réseaux génératifs antagonistes (GANs)

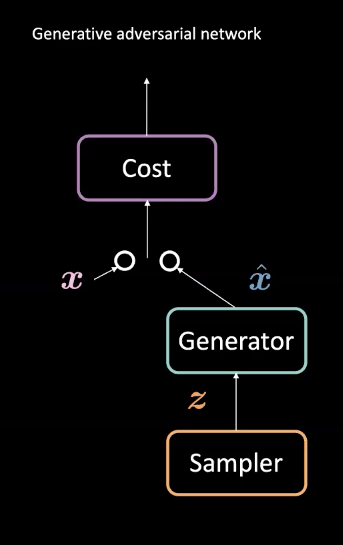
Figure 1 : Architecture d’un GAN

Les GANs sont un type de réseau de neurones utilisé pour l’apprentissage machine non supervisé. Ils sont composés de deux modules antagonistes : les réseaux générateur et coût. Ces modules se font concurrence de telle sorte que le réseau coût tente de filtrer les faux exemples tandis que le générateur tente de tromper ce filtre en créant des exemples réalistes $\vect{\hat{x}}$. Grâce à cette compétition, le générateur du modèle apprend à créer des données réalistes. Ces données peuvent être utilisées dans des tâches telles que la prédiction future ou pour générer des images spécialisées suite à un entraînement sur un jeu de données particulier.

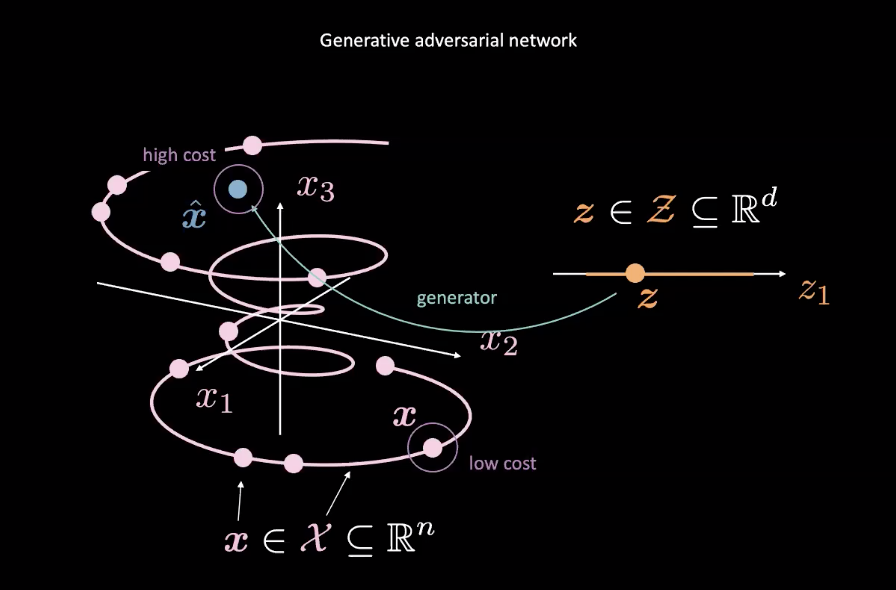
Figure 2 : GAN à partir d'une variable aléatoire

Les GANs sont des exemples de modèles à base d’énergie (EBMs). En tant que tel, le réseau coût est entraîné à produire des coûts faibles pour les entrées les plus proches de la distribution réelle des données, désignée par le $\vect{x}$ rose dans la figure 2. Les données provenant d’autres distributions, comme le $\vect{\hat{x}}$ bleu de la figure 2, devraient avoir un coût élevé. Une perte d’erreur quadratique moyenne (MSE) est généralement utilisée pour calculer la performance du réseau de coût. Il convient de noter que la fonction de coût produit une valeur scalaire positive dans une plage spécifiée c’est-à-dire $\text{coût} : \mathbb{R}^n \rightarrow \mathbb{R}^+ \cup {0}$). Ceci est différent d’un discriminateur classique qui utilise une classification discrète pour ses sorties.

Pendant ce temps, le réseau générateur ($\text{generateur} : \mathcal{Z} \rightarrow \mathbb{R}^n$) est entraîné à améliorer la correspondance de la variable aléatoire $\vect{z}$ aux données réalistes $\vect{\hat{x}}$ générées pour tromper le réseau de coût. Le générateur est entraîné par rapport à la sortie du réseau de coût, en essayant de minimiser l’énergie de $\vect{\hat{x}}$. Nous désignons cette énergie par $C(G(\vect{z}))$, où $C(\cdot)$ est le réseau coût et $G(\cdot)$ est le réseau générateur.

L’entraînement du réseau coût est basée sur la minimisation de la perte MSE, tandis que l’entraînement du réseau générateur est basée sur la minimisation du réseau coût, en utilisant des gradients de $C(\vect{\hat{x}})$ par rapport à $\vect{\hat{x}}$.

Pour garantir qu’un coût élevé est attribué aux points situés à l’extérieur de la variété de données et qu’un coût faible est attribué aux points situés à l’intérieur de la variété, la fonction de perte pour le réseau coût $\mathcal{L}_{C}$ est $C(x)+[m-C(G(\vect{z}))]^+$ pour une certaine marge positive $m$. Pour minimiser $\mathcal{L}_{C}$, il faut que $C(\vect{x}) \rightarrow 0$ et $C(G(\vect{z}) \rightarrow m$. La perte pour le générateur $\mathcal{L}_{G}$ est simplement $C(G(\vect{z}))$, ce qui encourage le générateur à s’assurer que $C(G(\vect{z})) \rightarrow 0$. Cependant, cela crée une instabilité car 0$ \leftarrow C(G(\vect{z})) \rightarrow m$.

Différence entre les GANs et les VAEs

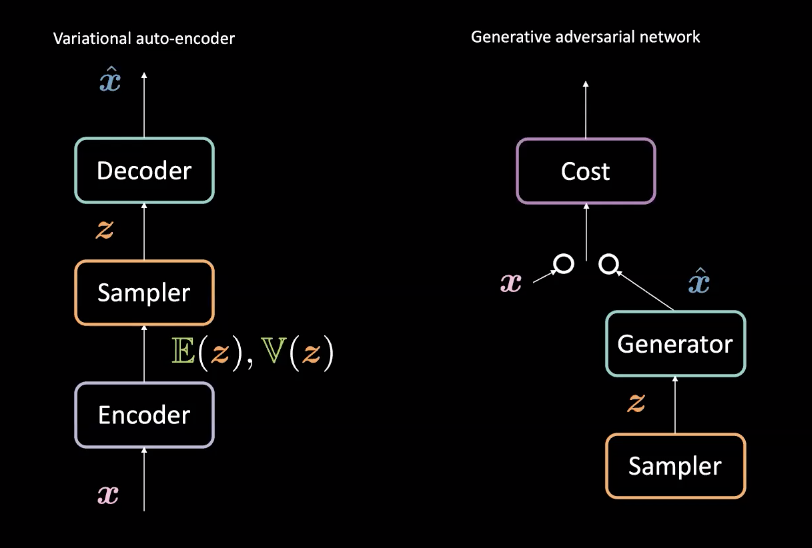
Figure 3 : VAE (gauche) vs GAN (droite)

Par rapport aux VAEs de la semaine 8, les GANs créent des générateurs légèrement différents. Rappelons que les VAE associent les entrées $\vect{x}$ vers un espace latent $\mathcal{Z}$ avec un encodeur puis associent $\mathcal{Z}$ vers l’espace de données avec un décodeur pour obtenir $\vect{\hat{x}}$. Ils utilisent ensuite la perte de reconstruction pour pousser $\vect{x}$ et $\vect{\hat{x}}$ à être similaires. Les GANs en revanche sont entrainés dans un cadre antagoniste avec les réseaux générateur et coût qui sont en concurrence comme décrit ci-dessus. Ces réseaux sont successivement entraînés par rétropropagation au moyen de méthodes basées sur le gradient. Une comparaison des différences architecturales est présentée à la figure 3.

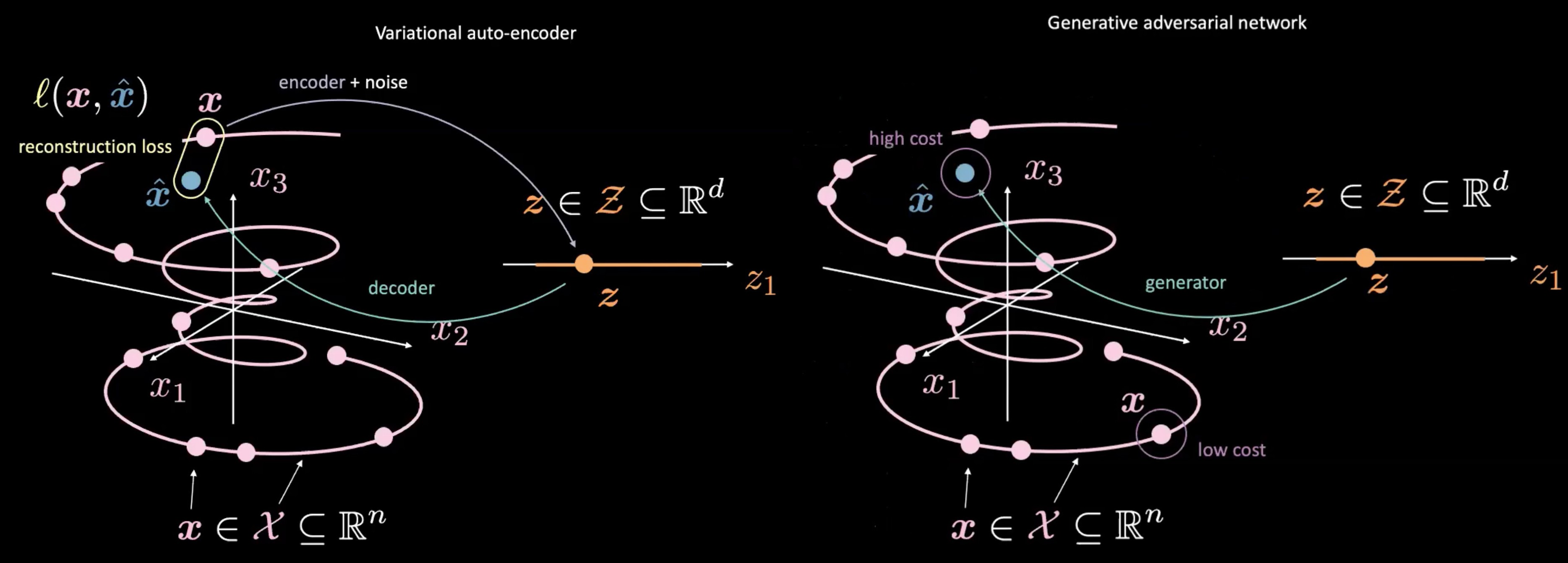
Figure 4 : VAE (gauche) vs GAN (droite) - à partir d'un échantillon aléatoire $\vect{z}$

Les GANs diffèrent également des VAEs par la façon dont ils produisent et utilisent les $vect{z}$. Les GANs commencent par échantillonner $\vect{z}$, comme l’espace latent dans un VAE. Ils utilisent ensuite un réseau génératif pour mettre en correspondance $\vect{z}$ avec $\vect{\hat{x}}$. Ce $\vect{\hat{x}}$ est envoyé à travers un réseau discriminateur/coût pour évaluer son caractère « réel ». Une des principales différences entre le VAE et le GAN est que nous n’avons pas besoin de mesurer une relation directe (c’est-à-dire la perte de reconstruction) entre la sortie du réseau générateur $\vect{\hat{x}}$ et les données réelles $\vect{x}$. Au lieu de cela, nous forçons $\vect{\hat{x}}$ à être similaire à $\vect{x}$ en entraînant le générateur à produire $\vect{\hat{x}}$ de telle sorte que le réseau discriminateur/coût produise des scores similaires à ceux des données réelles $\vect{x}$.

Les principaux pièges avec les GANs

Si les GANs peuvent être puissants pour la construction de générateurs, ils présentent quelques pièges importants.

1. Convergence instable

Au fur et à mesure que le générateur s’améliore avec l’entraînement, les performances du discriminateur se détériorent car celui-ci ne peut plus faire facilement la différence entre les données réelles et les fausses. Si le générateur est parfait, les données réelles et fausses se superposeront et le discriminateur créera de nombreuses erreurs de classification.

Cela pose un problème pour la convergence du GAN : le retour d’information du discriminateur devient moins significatif avec le temps. Si le GAN continue à s’entraîner au-delà du moment où le discriminateur donne un retour d’information complètement aléatoire, alors le générateur commence à s’entraîner sur le retour d’information indésirable et sa qualité peut s’effondrer (cf. la convergence de l’entraînement dans les GANs).

En raison de cette nature contradictoire entre le générateur et le discriminateur, il existe un point d’équilibre instable plutôt qu’un équilibre.

2. Disparition du gradient

Envisageons d’utiliser la perte binaire d’entropie croisée pour un GAN :

Au fur et à mesure que le discriminateur devient plus confiant, $D(\vect{x})$ se rapproche de $1$ et $D(\vect{\hat{x}})$ se rapproche de $0$. Cette confiance déplace les sorties du réseau coût vers des régions plus plates où les gradients sont plus saturés. Ces régions plus plates présentent de petits gradients qui disparaissent et qui entravent l’entraînement du réseau générateur. Ainsi, lorsque de l’entraînement d’un GAN, il faut nous assurer que le coût augmente progressivement à mesure que nous devenons plus confiant.

3. Effondrement des modes

Si un générateur fait correspondre tous les $\vect{z}$ de l’échantillonneur à un seul $\vect{\hat{x}}$ qui peut tromper le discriminateur, alors le générateur produira seulement ce $\vect{\hat{x}}$. Finalement, le discriminateur apprendra à détecter spécifiquement cette fausse entrée. En conséquence, le générateur trouve simplement le $\vect{\hat{x}}$ suivant le plus plausible et le cycle continue. Par conséquent, le discriminateur se retrouve piégé dans les minima locaux pendant qu’il passe en revue les faux $\vect{\hat{x}}$. Une solution possible à ce problème est d’imposer une pénalité au générateur pour avoir toujours donné la même sortie avec des entrées différentes.

Code source du Deep Convolutional Generative Adversarial Network (DCGAN)

Le code source de l’exemple peut être trouvé ici.

Générateur

1. Le générateur suréchantillonne l’entrée en utilisant plusieurs modules nn.ConvTranspose2d séparés par nn.BatchNorm2d et nn.ReLU.
2. A la fin de la séquence, le réseau utilise nn.Tanh() pour écraser les sorties à $(-1,1)$.
3. Le vecteur aléatoire d’entrée est de taille $nz$. La sortie est de taille $nc \times 64 \times 64$, où $nc$ est le nombre de canaux.

class Generator(nn.Module):
    def __init__(self):
        super().__init__()
        self.main = nn.Sequential(
            # l'entrée Z va dans une convolution
            nn.ConvTranspose2d(     nz, ngf * 8, 4, 1, 0, bias=False),
            nn.BatchNorm2d(ngf * 8),
            nn.ReLU(True),
            # état de taille (ngf*8) x 4 x 4
            nn.ConvTranspose2d(ngf * 8, ngf * 4, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ngf * 4),
            nn.ReLU(True),
            # état de taille (ngf*4) x 8 x 8
            nn.ConvTranspose2d(ngf * 4, ngf * 2, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ngf * 2),
            nn.ReLU(True),
            # état de taille (ngf*2) x 16 x 16
            nn.ConvTranspose2d(ngf * 2,     ngf, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ngf),
            nn.ReLU(True),
            # état de taille (ngf) x 32 x 32
            nn.ConvTranspose2d(    ngf,      nc, 4, 2, 1, bias=False),
            nn.Tanh()
            # état de taille (nc) x 64 x 64
        )

    def forward(self, input):
        output = self.main(input)
        return output

Discriminateur

1. Il est important d’utiliser nn.LeakyReLU comme fonction d’activation pour éviter de tuer les gradients dans les régions négatives. Sans ces gradients, le générateur ne recevra pas de mises à jour.
2. A la fin de la séquence, le discriminateur utilise nn.Sigmoid() pour classer l’entrée.

class Discriminator(nn.Module):
    def __init__(self):
        super().__init__()
        self.main = nn.Sequential(
            # l'entrée est (nc) x 64 x 64
            nn.Conv2d(nc, ndf, 4, 2, 1, bias=False),
            nn.LeakyReLU(0.2, inplace=True),
            # état de taille (ndf) x 32 x 32
            nn.Conv2d(ndf, ndf * 2, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ndf * 2),
            nn.LeakyReLU(0.2, inplace=True),
            # état de taille (ndf*2) x 16 x 16
            nn.Conv2d(ndf * 2, ndf * 4, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ndf * 4),
            nn.LeakyReLU(0.2, inplace=True),
            # état de taille (ndf*4) x 8 x 8
            nn.Conv2d(ndf * 4, ndf * 8, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ndf * 8),
            nn.LeakyReLU(0.2, inplace=True),
            # état de taille (ndf*8) x 4 x 4
            nn.Conv2d(ndf * 8, 1, 4, 1, 0, bias=False),
            nn.Sigmoid()
        )

    def forward(self, input):
        output = self.main(input)
        return output.view(-1, 1).squeeze(1)

Ces deux classes sont initialisées comme netG et netD.

Fonction de perte pour le GAN

Nous utilisons l’entropie croisée binaire (BCE) entre la cible et la sortie.

criterion = nn.BCELoss()

Configuration

Nous mettons en place un fixed_noise de taille opt.batchSize et de longueur du vecteur aléatoire nz. Nous créons également des labels pour les données réelles et les données générées (fausses) appelées respectivement real_label et fake_label.

fixed_noise = torch.randn(opt.batchSize, nz, 1, 1, device=device)
real_label = 1
fake_label = 0

Ensuite, nous mettons en place des optimiseurs pour les réseaux discriminateurs et générateurs.

optimizerD = optim.Adam(netD.parameters(), lr=opt.lr, betas=(opt.beta1, 0.999))
optimizerG = optim.Adam(netG.parameters(), lr=opt.lr, betas=(opt.beta1, 0.999))

Entraînement

Chaque époque d’entraînement est divisée en deux étapes.
L’étape 1 consiste à mettre à jour le réseau discriminateur. Elle se fait en deux parties. Tout d’abord, on alimente le discriminateur en données réelles provenant des dataloaders, on calcule la perte entre la sortie et le real_label, puis on accumule des gradients avec la rétropropagation. Deuxièmement, nous alimentons le discriminateur en données générées par le réseau générateur en utilisant le fixed_noise, nous calculons la perte entre la sortie et le fake_label, et ensuite nous accumulons le gradient. Enfin, nous utilisons les gradients accumulés pour mettre à jour les paramètres du réseau discriminateur.

A noter que nous détachons les fausses données pour empêcher les gradients de se propager vers le générateur pendant que nous entraînons le discriminateur.
A noter également que nous n’avons besoin d’appeler zero_grad() qu’une seule fois au début pour effacer les gradients afin que les gradients des données réelles et fausses puissent être utilisés pour la mise à jour. Les deux appels .backward() accumulent ces gradients. Nous n’avons finalement besoin que d’un seul appel de optimizerD.step() pour mettre à jour les paramètres.

# entraîner avec le vrai
netD.zero_grad()
real_cpu = data[0].to(device)
batch_size = real_cpu.size(0)
label = torch.full((batch_size,), real_label, device=device)

output = netD(real_cpu)
errD_real = criterion(output, label)
errD_real.backward()
D_x = output.mean().item()

# entraîner avec le faux
noise = torch.randn(batch_size, nz, 1, 1, device=device)
fake = netG(noise)
label.fill_(fake_label)
output = netD(fake.detach())
errD_fake = criterion(output, label)
errD_fake.backward()
D_G_z1 = output.mean().item()
errD = errD_real + errD_fake
optimizerD.step()

L’étape 2 consiste à mettre à jour le réseau générateur. Cette fois, nous alimentons le discriminateur en fausses données, mais nous calculons la perte avec le real_label ! Le but de cette opération est d’entraîner le générateur à faire des $\vect{\hat{x}}$ réalistes.

netG.zero_grad()
label.fill_(real_label)  # Les fausses étiquettes sont réelles pour la fonction de coût du générateur
output = netD(fake)
errG = criterion(output, label)
errG.backward()
D_G_z2 = output.mean().item()
optimizerG.step()