Modèles du monde et réseaux génératifs antagonistes

Modèles du monde pour le contrôle autonome

L’une des utilisations les plus importantes de l’apprentissage autosupervisé est l’apprentissage de modèles du monde pour le contrôle. Lorsque les humains effectuent une tâche, ils disposent d’un modèle interne pour le fonctionnement du monde. Par exemple, nous acquérons une intuition pour la physique à l’âge de 9 mois environ, principalement par l’observation. Dans un certain sens, cela ressemble à l’apprentissage autosupervisé. En apprenant à prédire ce qui va se passer, nous apprenons des principes abstraits, tout comme les modèles autosupervisés apprennent des caractéristiques latentes. Mais en allant plus loin, les modèles internes nous permettent d’agir sur le monde. Par exemple, nous pouvons utiliser notre intuition en physique et notre compréhension du fonctionnement de nos muscles pour prédire (et exécuter) comment attraper un stylo qui tombe.

Qu’est-ce qu’un modèle du monde (world model) ?

Un système intelligent autonome comprend quatre grands modules (figure 1). Tout d’abord, le module de perception observe le monde et calcule une représentation de l’état du monde. Cette représentation est incomplète parce que :
1) l’agent n’observe pas l’univers en entier
2) la précision des observations est limitée.
Il est également intéressant de noter que dans le modèle feed-forward, le module de perception n’est présent que pour le pas de temps initial. Deuxièmement, le module acteur (également appelé module politique) imagine une action basée sur l’état (représenté) du monde.
Troisièmement, le module modèle prédit le résultat de l’action en fonction de l’état (représenté) du monde, et peut-être aussi en fonction de certaines caractéristiques latentes. Cette prédiction est transmise au pas de temps suivant en tant que supposition de l’état suivant du monde, en prenant le rôle du module de perception à partir du pas de temps initial. La figure 2 présente une démonstration détaillée de ce processus d’anticipation.
Enfin, le module critique transforme cette même prédiction en un coût de réalisation de l’action proposée. Par exemple étant donné la vitesse à laquelle je crois que le stylo tombe, si je bouge les muscles de cette manière particulière, à quel point vais-je rater la prise ?

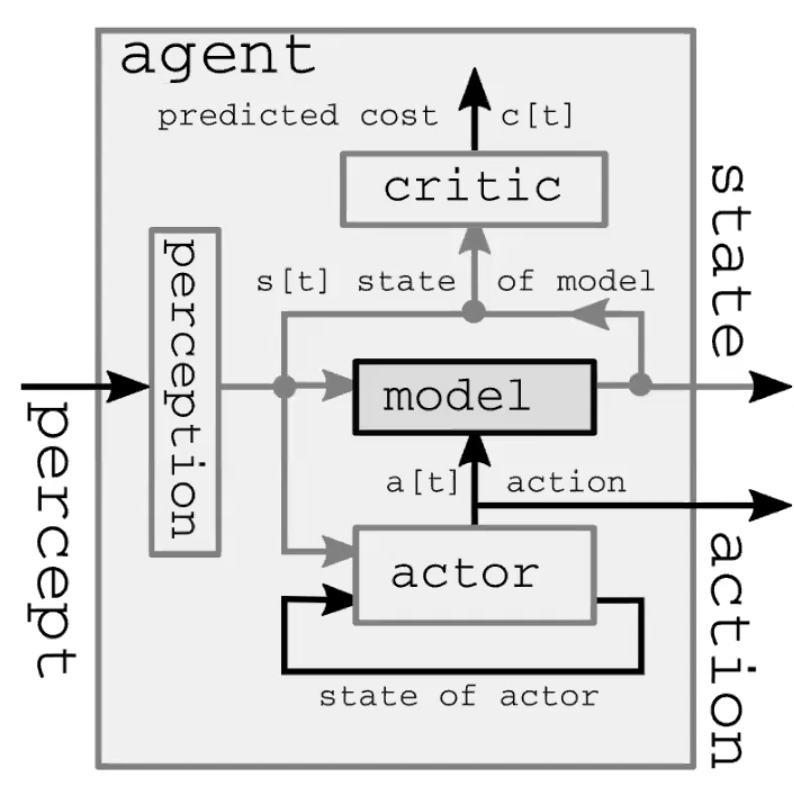
Figure 1 : Architecture d’un modèle du monde d’un système intelligent autonome

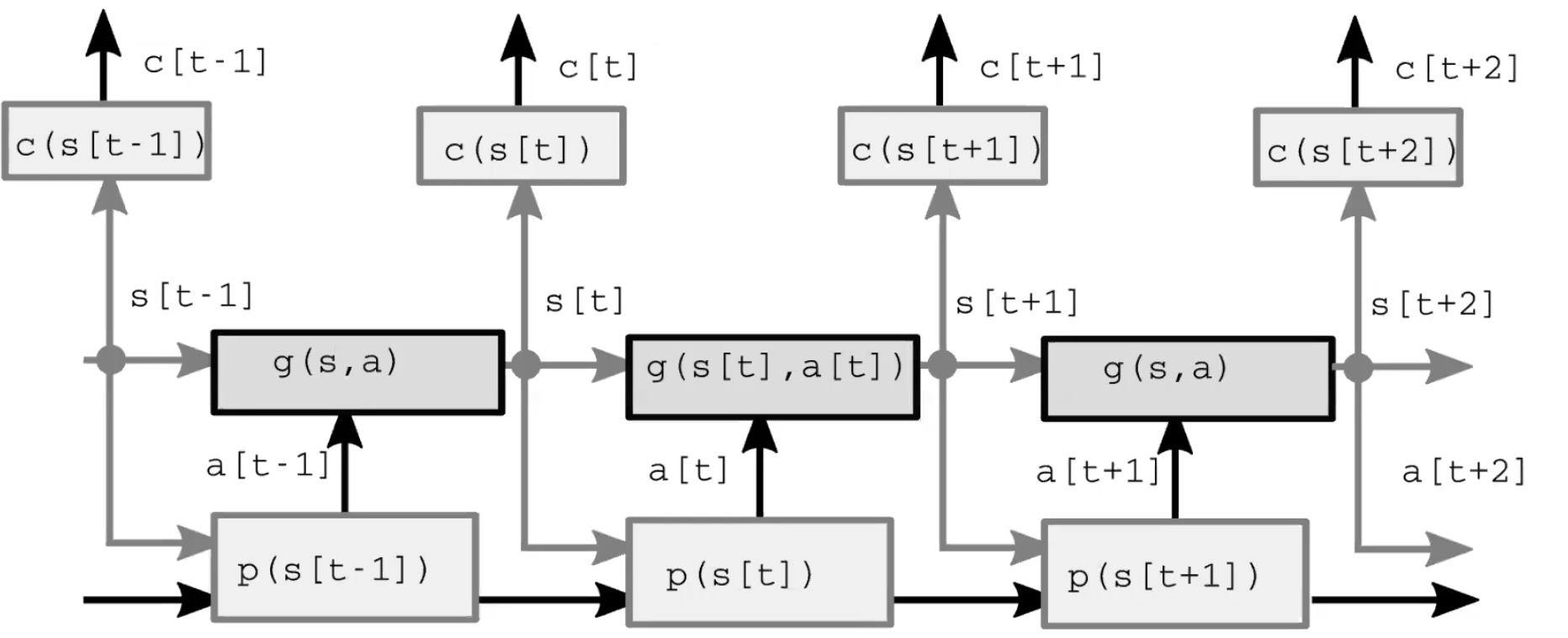
Figure 2 : Architecture du modèle

Le cadre classique

Dans le cadre classique du contrôle, il n’y a pas de module acteur/politique, mais plutôt une variable d’action. Cette formulation est optimisée par une méthode classique appelée « Model Predictive Control » qui a été utilisée par la NASA dans les années 1960 pour calculer les trajectoires des fusées lorsqu’elles sont passées des ordinateurs humains (principalement des mathématiciennes noires) aux ordinateurs électroniques. Nous pouvons considérer ce système comme un RNN déroulé et les actions comme des variables latentes. On peut utiliser des méthodes de rétropropagation et de gradient (ou éventuellement d’autres méthodes, comme la programmation dynamique pour un ensemble d’actions discrètes) pour inférer la séquence d’actions qui minimise la somme des coûts des pas de temps.

Note : nous utilisons le mot « inférence » pour les variables latentes et « apprentissage » pour les paramètres, bien que le processus d’optimisation de ceux-ci soit généralement similaire. Une différence importante est qu’une variable latente prend une valeur spécifique pour chaque échantillon, alors que les paramètres sont partagés entre les échantillons.

Une amélioration

Nous préférons ne pas passer par le processus compliqué de la rétropropagation chaque fois que nous voulons faire un plan. Pour y remédier, nous utilisons la même astuce que pour l’auto-encodeur variationnel pour améliorer le codage épars : nous entraînons un encodeur à prédire directement la séquence d’action optimale à partir des représentations du monde. Dans ce régime, l’encodeur est appelé un réseau politique.

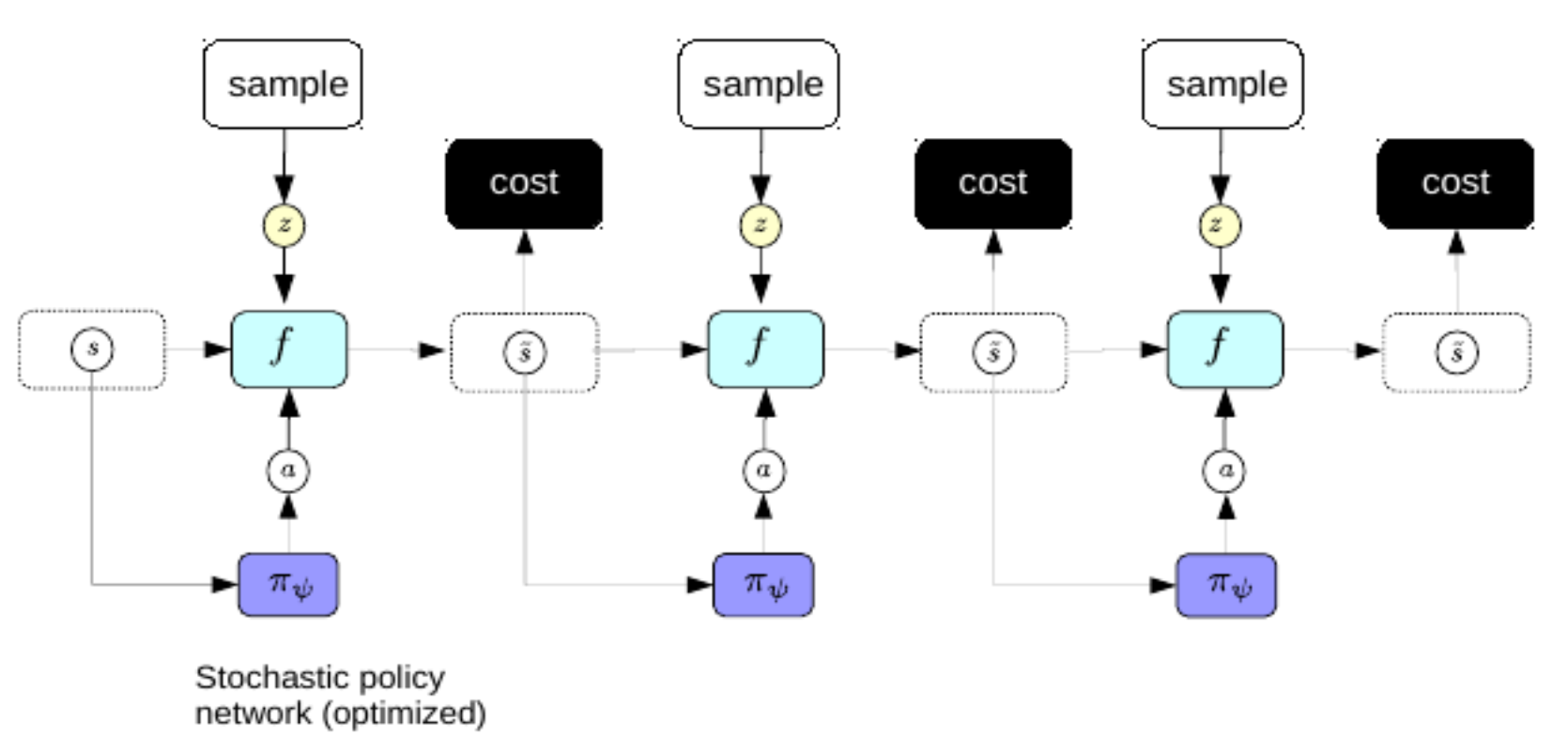
Figure 3 : Réseau politique

Une fois entraînés, nous pouvons utiliser les réseaux politiques pour prédire la séquence d’action optimale immédiatement après la perception.

Apprentissage par renforcement

Les principales différences entre l’apprentissage par renforcement (nous le noterons RL dans la suite, d’après le terme anglais Reinforcement learning) et ce que nous avons étudié jusqu’à présent sont de deux ordres : 1) Dans les environnements d’apprentissage par renforcement, la fonction de coût est une boîte noire. En d’autres termes, l’agent ne comprend pas la dynamique de la récompense. 2) Dans le cadre du RL, nous n’utilisons pas un modèle de prédiction du monde. Au lieu de cela, nous interagissons avec le monde réel et apprenons le résultat en observant ce qui se passe. Dans le monde réel, notre mesure de l’état du monde est imparfaite et il n’est donc pas toujours possible de prédire ce qui se passera ensuite.

Le principal problème du RL est que la fonction de coût n’est pas différenciable. Cela signifie que la seule façon d’apprendre est de procéder par essais et erreurs. Le problème devient alors de savoir comment explorer efficacement l’espace des états. Une fois que vous avez trouvé une solution à ce problème, la question qui suit est celle fondamentale de l’exploration vs l’exploitation : préférez-vous prendre des actions pour apprendre le plus possible sur l’environnement ou plutôt exploiter ce que vous avez déjà appris pour obtenir une récompense aussi élevée que possible ?

Les méthodes Acteur-Critique sont une famille populaire d’algorithmes de RL qui entraînent à la fois un acteur et un critique. De nombreuses méthodes de RL fonctionnent de manière similaire, en entraînant un modèle de la fonction de coût (le critique). Dans les méthodes Acteur-Critique, le rôle du critique est d’apprendre la valeur attendue de la fonction de valeur. Cela permet de faire une rétropropagation dans le module, puisque le critique n’est qu’un réseau neuronal. La responsabilité de l’acteur est de proposer des actions à entreprendre dans l’environnement. Le rôle du critique est d’apprendre un modèle de la fonction de coût. L’acteur et le critique travaillent en tandem, ce qui permet un apprentissage plus efficace que si aucun critique n’est utilisé. Sans un bon modèle du monde, il est beaucoup plus difficile d’apprendre. Par exemple, la voiture à côté de la falaise ne saura pas que tomber d’une falaise est une mauvaise idée.

Un modèle du monde permet aux humains et plus généralement aux animaux d’apprendre beaucoup plus rapidement que les agents du RL. Nous avons de très bons modèles du monde dans notre tête.

Nous ne pouvons pas toujours prédire l’avenir du monde en raison de l’incertitude inhérente : l’incertitude aléatoire et épistémique. L’incertitude aléatoire est due à des choses ne pouvant pas être contrôlé ou observé dans l’environnement. L’incertitude épistémique, est quand il n’est pas possible de prédire l’avenir du monde car le modèle ne contient pas assez de données d’entraînement.

Le modèle de prédiction aimerait pouvoir prédire

où $z$ est une variable latente dont nous ne connaissons pas la valeur. $z$ représente ce que nous ne pouvons pas savoir sur le monde mais qui influence quand même la prédiction (c’est-à-dire l’incertitude aléatoire). On peut régulariser $z$ avec parcimonie, du bruit ou avec un encodeur. Nous pouvons utiliser des modèles de prédiction pour apprendre à planifier. Le système fonctionne en ayant un décodeur décodant une concaténation de la représentation d’état et de l’incertitude $z$. Le meilleur $z$ est défini comme celui qui minimise la différence entre $\hat s_{t+1}$ et le $s_{t+1}$ effectivement observé.

Réseaux génératifs antagonistes

Il existe de nombreuses variantes des réseaux génératifs antagonistes (GANs pour Generative Adversarial Networks). Nous considérons ici le GAN comme une forme de modèle à base d’énergie utilisant des méthodes contrastives. Il augmente l’énergie des échantillons contrastifs et diminue l’énergie des échantillons d’entraînement. Un GAN de base se compose de deux parties : un générateur qui produit des échantillons contrastifs de manière intelligente et un discriminateur (parfois appelé critique) qui est essentiellement une fonction de coût agissant comme un modèle énergétique. Le générateur et le discriminateur sont tous deux des réseaux neuronaux.

Les deux types d’entrée dans le GAN sont respectivement des échantillons d’entraînement et des échantillons contrastifs. Pour les échantillons d’entraînement, le GAN les fait passer à travers le discriminateur et baisse leur énergie. Pour les échantillons contrastifs, le GAN échantillonne les variables latentes d’une certaine distribution, les fait passer par le générateur pour produire quelque chose de similaire aux échantillons d’entraînement et les fait passer par le discriminateur pour faire monter leur énergie. La fonction de perte pour le discriminateur est la suivante :

où $L_d$ peut être une fonction de perte avec marge comme $F(y) + [m - F(\bar{y})]^+$ ou $\log(1 + \exp[F(y)]) + \log(1 + \exp[-F(\bar{y})])$ tant que cela fait diminuer $F(y)$ et augmenter $F(\bar{y})$. Dans ce contexte, $y$ est le label et $\bar{y}$ est la variable réponse qui donne l’énergie la plus faible sauf $y$ lui-même.

La fonction de perte est différente pour le générateur :

où $z$ est la variable latente et $G$ est le réseau générateur. Nous voulons faire en sorte que le générateur adapte son poids et produise $\bar{y}$ avec une faible énergie pouvant tromper le discriminateur.

La raison pour laquelle ce type de modèle est appelé réseaux génératifs antagonistes est que nous avons deux fonctions objectives qui sont incompatibles l’une avec l’autre et que nous devons les minimiser simultanément. Ce n’est pas un problème de descente de gradient car le but est de trouver un équilibre de Nash entre ces deux fonctions or la descente de gradient n’en est pas capable par défaut.

Il y aura des problèmes lorsque nous aurons des échantillons qui seront proches de la vraie variété. Supposons que nous ayons une surface infiniment fine. Le discriminateur doit produire une probabilité de $0$ à l’extérieur de la variété et une probabilité infinie sur la variété. Comme cela est très difficile à réaliser, le GAN utilise une sigmoïde pour produire $0$ en dehors de la variété et $1$ sur la variété. Le problème est que si nous entraînons le système avec succès en faisant en sorte que le discriminateur produise $0$ en dehors de la variété, la fonction d’énergie est complètement inutile. En effet, la fonction d’énergie n’est pas homogène car toute l’énergie en dehors de la variété de données sera infinie et toute l’énergie sur la variété de données sera nulle. Nous ne voulons pas que la valeur de l’énergie passe de $0 $ à l’infini en un tout petit pas. Les chercheurs ont proposé de nombreux moyens pour résoudre ce problème en régularisant la fonction d’énergie. Un bon exemple de GAN amélioré est le GAN de Wasserstein qui limite la taille du poids du discriminateur.