Auto-encodeurs discriminants récurrents épars et l’éparsité de groupe

Auto-encodeurs discriminants récurrents épars (Discriminative recurrent sparse autoencoder : DrSAE)

L’idée des DrSAEs consiste à combiner un codage épars ou l’auto-encodeur épars avec un entraînement discriminant.

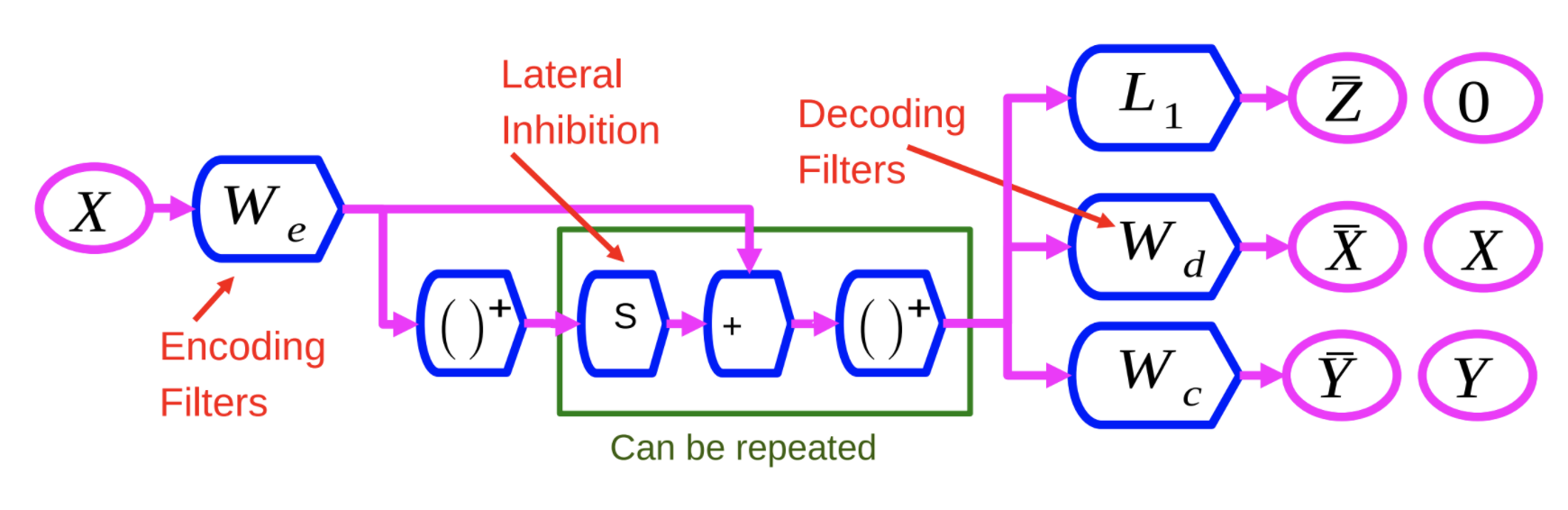
Figure 1 : Réseau DrSAE

L’encodeur $W_e$ est similaire à celui de la méthode LISTA. La variable $X$ est passée par $W_e$, puis par une non-linéarité. Ce résultat est ensuite multiplié par une autre matrice apprise, $S$, et ajouté à $W_e$. Il est ensuite envoyé à travers une autre non-linéarité. Ce processus peut être répété un certain nombre de fois, chaque répétition constituant une couche.

Nous entraînons ce réseau de neurones avec 3 critères différents :

1. $L_1$ : appliquer le critère $L_1$ sur le vecteur d’entités $Z$ pour le rendre épars.
2. Reconstruire $X$ : ceci est fait en utilisant une matrice de décodage qui reproduit l’entrée sur la sortie. Ceci est fait en minimisant l’erreur quadratique, indiquée par $W_d$ dans la figure 1.
3. Ajouter un troisième terme : ce troisième terme, indiqué par $W_c$, est un simple classifieur linéaire qui tente de prédire une catégorie.

Le système est entraîné à minimiser ces trois critères en même temps.

L’avantage de cette méthode est de forcer le système à trouver des représentations qui peuvent reconstruire l’entrée, puis nous biaisons le système vers l’extraction de caractéristiques qui contiennent autant d’informations sur l’entrée que possible. En d’autres termes, cela enrichit les caractéristiques.

Eparsité de groupe

L’idée ici est de générer des caractéristiques éparses, c’est-à-dire pas seulement des caractéristiques normales qui sont extraites par des convolutions mais de produire essentiellement des caractéristiques qui sont éparses après le pooling.

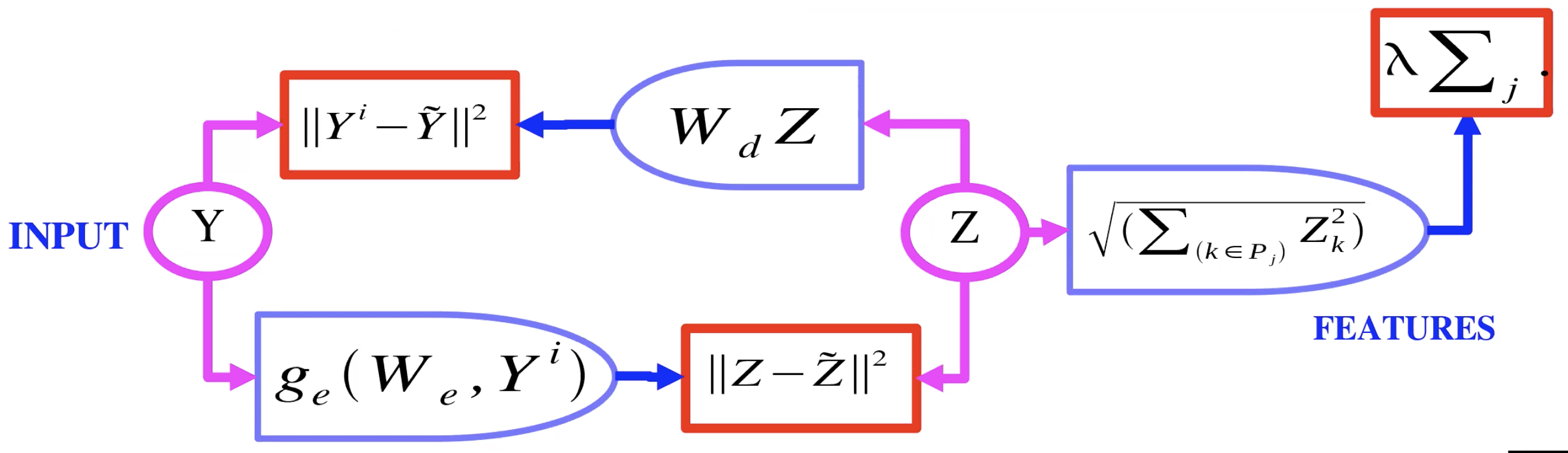
Figure 2 : Auto-encodeur avec éparsité de groupe

La figure 2 montre un exemple d’auto-encodeur avec éparsité de groupe. Ici, au lieu de la variable latente $Z$ passant par une $L_1$, elle passe par une $L_2$ sur les groupes. Nous prenons donc la norme $L_2$ pour chaque composant dans un groupe de $Z$ et effectuons la somme de ces normes. C’est donc ce qui est utilisé comme régulariseur afin que nous puissions avoir une certaine éparsité dans les groupes de $Z$. Ces groupes de caractéristiques ont tendance à regrouper des caractéristiques qui sont similaires les unes aux autres.

Auto-encodeur avec éparsité de groupe : questions des étudiants

Une stratégie similaire à celle utilisée dans la première diapositive avec le classifieur et le régulariseur peut-elle être appliquée pour les VAEs ?

Ajouter du bruit et forcer l’éparsité dans un VAE sont deux moyens de réduire l’information de la variable latente. Cela empêche l’apprentissage d’une fonction d’identité.

Dans la diapositive « AE with Group Sparsity », qu’est-ce que $P_j$ ?

$p$ est un pool de caractéristiques. Pour un vecteur $z$, ce serait un sous-ensemble des valeurs de $z$.

Clarification sur le pooling des caractéristiques.

L’encodeur produit une variable latente $z$ qui est régularisée en utilisant la norme $L_2$ des caractéristiques mises en commun. Cette variable $z$ est utilisée par le décodeur pour la reconstruction de l’image.

La régularisation des groupes aide-t-elle à regrouper des caractéristiques similaires ?

La réponse n’est pas claire, le travail effectué ici a été fait avant que la puissance de calcul/les données ne soient facilement disponibles. Les techniques n’ont pas été remises au premier plan.

Entraînement au niveau de l’image, filtres locaux mais pas de partage de poids

La réponse à la question de savoir si cela aide n’est pas claire. Les personnes travaillant sur le sujet s’intéressent soit à la restauration d’images, soit à une sorte d’apprentissage autosupervisé. Cela fonctionnerait plutôt bien lorsque le jeu de données est très réduit. Lorsque nous avons un encodeur et un décodeur convolutifs et entraînons avec l’éparsité de groupe sur des cellules complexes, après avoir terminé l’entraînement, le système nous débarrasse du décodeur et n’utilise l’encodeur que comme un extracteur de caractéristiques. Nous pouvons alors coller une deuxième couche par-dessus.

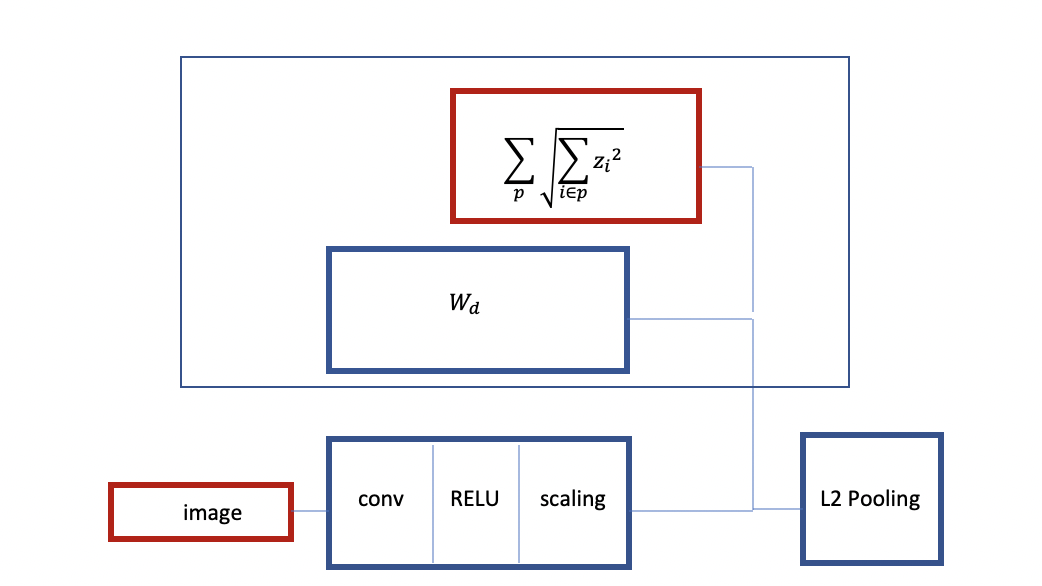
Figure 3 : Structure d’un ConvNet avec ReLU et éparsité de groupe

Comme on peut le voir ci-dessus, nous commençons avec une image, nous avons un encodeur qui est en fait une convolution puis une ReLU et une sorte de couche de mise à l’échelle. Nous entrainons avec une éparsité de groupe. Nous avons un décodeur linéaire et un critère qui est le groupe par 1. Nous prenons l’éparsité de groupe comme régularisation. C’est comme le pooling L2 avec une architecture similaire à l’éparsité de groupe.
Nous pouvons aussi entraîner une autre instance de ce réseau. Cette fois, en ajoutant d’autres couches et en ayant un décodeur avec le polling L2 et le critère d’éparsité. On entraîne alors à reconstruire l’entrée avec le pooling au-dessus. Cela crée un ConvNet à deux couches pré-entraîné. Cette procédure est également appelée stacked autoencoder. La principale caractéristique de cette procédure est qu’elle est entraînée à produire des caractéristiques invariantes avec une éparsité de groupe.

Devrions-nous utiliser tous les sous-arbres possibles comme groupes ?

C’est à vous de décider, vous pouvez utiliser plusieurs arbres si vous le souhaitez. Nous pouvons entraîner l’arbre avec un arbre plus grand que nécessaire et ensuite retirer les branches rarement utilisées.

Figure 4 : Entraînement au niveau de l'image, filtres locaux mais pas de partage du poids

C’est ce qu’on appelle les pinwheel patterns (motifs en forme de pales de turbines). C’est une sorte d’organisation des caractéristiques. L’orientation varie continuellement lorsque vous contournez ces points rouges. Si nous prenons un de ces points rouges et si nous faisons un petit cercle autour des points rouges, nous remarquons que l’orientation de l’extracteur varie en quelque sorte continuellement lorsque nous nous déplaçons. Des tendances similaires sont observées dans le cerveau.

Le terme d’éparsité de groupe est-il entraîné à avoir une petite valeur ?

Il s’agit d’un régulariseur. Le terme lui-même n’est pas entraîné, il est fixe. C’est juste la norme L2 des groupes et les groupes sont prédéterminés. Mais, comme c’est un critère, il détermine ce que l’encodeur et le décodeur vont faire et quel type de caractéristiques seront extraites.

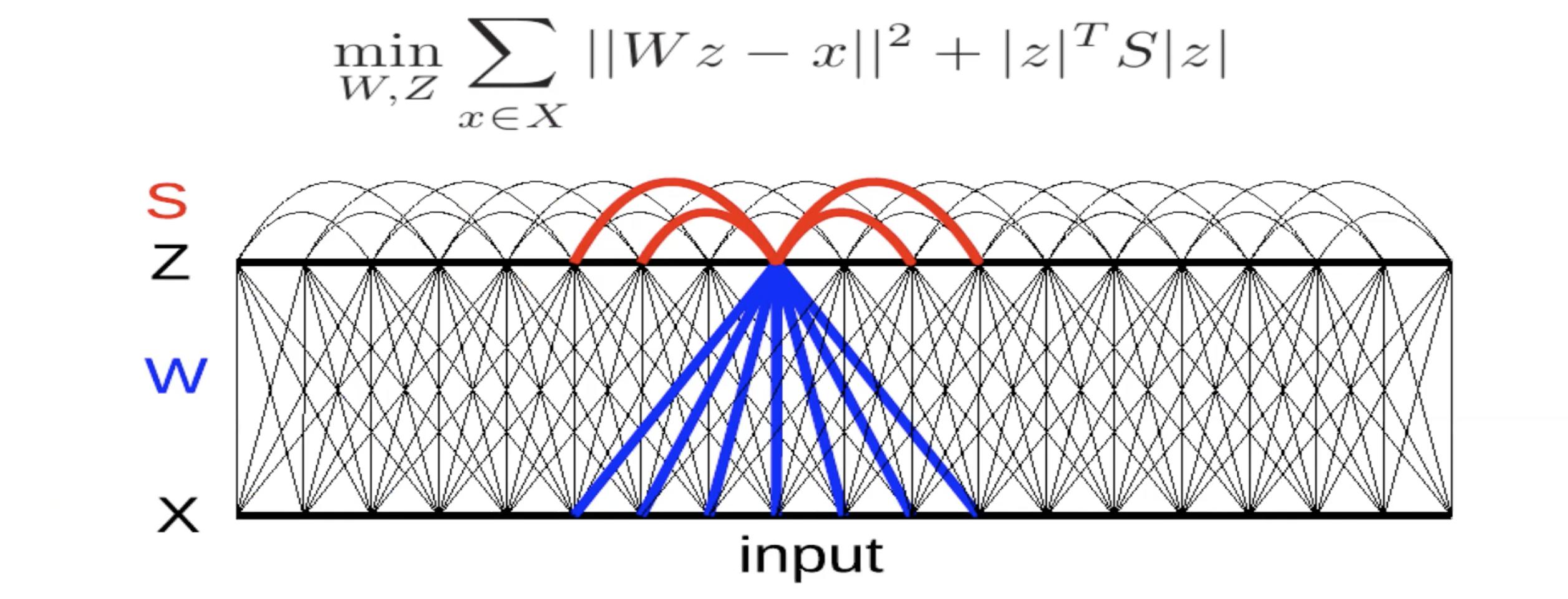
Figure 5 : Caractéristiques invariantes par inhibition latérale

Ici, il y a un décodeur linéaire avec une erreur de reconstruction quadratique. Il y a un critère dans l’énergie. La matrice $S$ est soit déterminée à la main, soit apprise de façon à maximiser ce terme. Si les termes dans $S$ sont positifs et grands, cela implique que le système ne veut pas que $z_i$ et $z_j$ soient allumés en même temps. Il s’agit donc d’une sorte d’inhibition mutuelle (appelée inhibition naturelle en neurosciences). Nous essayons donc de trouver une valeur pour $S$ qui soit la plus grande possible.

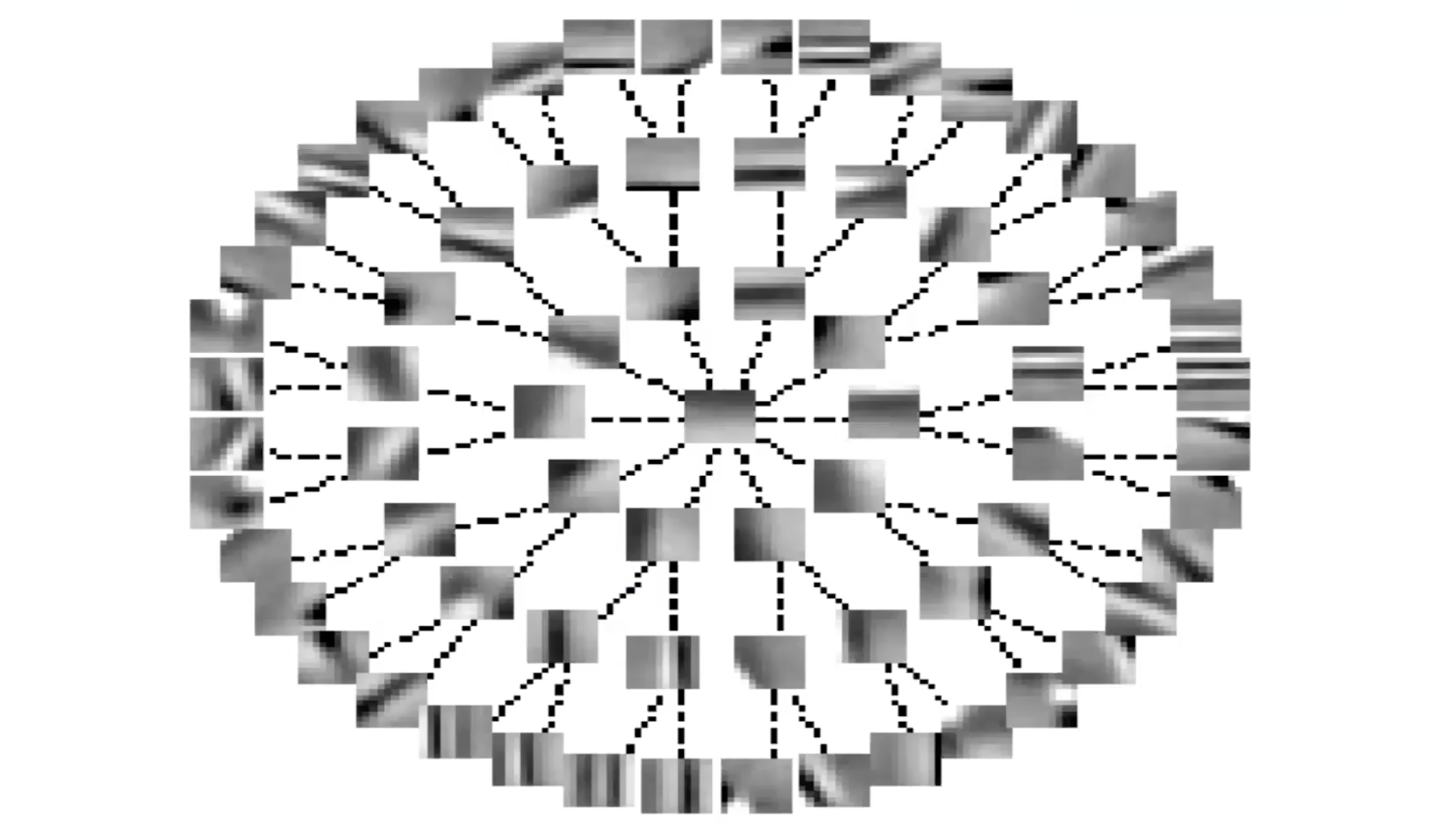
Figure 6 : Caractéristiques invariantes par inhibition latérale (forme d'arbre)

En organisant $S$ en termes d’arbre, les lignes représentent les termes nuls dans la matrice $S$. Chaque fois qu’il n’y a pas de ligne, il y a un terme non nul. Ainsi, chaque caractéristique inhibe toutes les autres caractéristiques, sauf celles qui sont en haut de l’arbre ou en bas de l’arbre. C’est un peu l’inverse de l’éparsité de groupe.
Nous voyons encore une fois que les systèmes organisent les caractéristiques de manière plus ou moins continue. Les caractéristiques le long de la branche d’un arbre représentent la même caractéristique avec différents niveaux de sélectivité. Les caractéristiques en périphérie varient plus ou moins.
Pour entraîner ce système, à chaque itération, nous donnons un $x$ et trouvons $z$ qui minimise cette fonction énergétique. Ensuite, nous faisons une étape de descente de gradient pour mettre à jour le $W$. Nous pouvons également faire une étape de montée de gradient pour augmenter les termes en $S$.