Architectures des RNNs et des LSTMs

Vue d’ensemble

Le RNN est un type d’architecture que nous pouvons utiliser pour traiter des séquences de données. Qu’est-ce qu’une séquence ? Le cours sur le RNN nous a appris qu’un signal peut être soit 1D, 2D ou 3D selon le domaine. Le domaine est défini par le point de départ et le point d’arrivée. Le traitement des données séquentielles concerne essentiellement les données 1D puisque le domaine est l’axe temporel. Néanmoins, il est possible d’utiliser le RNN pour traiter des données 2D où il y a deux directions.

Architecture standard vs le RNN

La figure 1 est un diagramme de réseau de neurones vanilla avec trois couches. « Vanilla » est un terme américain signifiant « standard / de base ». La bulle rose est le vecteur d’entrée $x$, au centre se trouve la couche cachée en vert et la dernière couche bleue est la sortie. En utilisant un exemple d’électronique numérique sur la droite de la figure, c’est comme une logique combinatoire où le courant de sortie ne dépend que du courant d’entrée.

Figure 1 : Architecture standard

Contrairement à un réseau de neurones standard, dans les RNNs la sortie du courant dépend non seulement de l’entrée mais aussi de l’état du système, comme le montre la figure 2. C’est comme une logique séquentielle en électronique numérique, où la sortie dépend également d’un interrupteur (une unité de mémoire de base dans l’électronique numérique). La principale différence ici est donc que la sortie d’un réseau neuronal standard ne dépend que de l’entrée, tandis que celle d’un RNN dépend également de l’état du système.

Figure 2 : Architecture RNN

Figure 3 : Architecture d’un réseau de neurones de base

Le diagramme utilisé par Yann ajoute des formes entre les neurones pour représenter l’association entre un tenseur et un autre (un vecteur à un autre). Par exemple, dans la figure 3, le vecteur d’entrée $x$ va correspondre à travers cet élément supplémentaire aux représentations cachées $h$. Cet élément est en fait une transformation affine, c’est-à-dire une rotation plus une distorsion. Ensuite, par une autre transformation, nous passons de la couche cachée à la sortie finale. De même, dans le diagramme RNN, il est possible d’avoir les mêmes éléments supplémentaires entre les neurones.

Figure 4 : L'architecture RNN de Yann

Quatre types d’architectures RNN et des exemples

Le premier cas est celui du « vector to sequence » (un vecteur en entrée du réseau et on obtient une sequence en sortie). L’entrée est la bulle rose. La succession des états internes du système est représentée par les bulles vertes. À mesure que l’état du système évolue, il y a une sortie spécifique à chaque étape, représentée par une bulle bleue.

Figure 5 : Vec to Seq

Un exemple de ce type d’architecture est d’avoir comme entrée une image et comme sortie une séquence de mots représentant les descriptions de l’image d’entrée. Pour expliquer l’utilisation de la figure 6, chaque bulle bleue peut être un index dans un dictionnaire de mots. Par exemple, si la sortie est la phrase « This is a yellow school bus » (« C’est un bus scolaire jaune »). Vous obtenez d’abord l’index du mot « This », puis l’index du mot « is », et ainsi de suite. Certains des résultats de ce réseau sont présentés ci-dessous. Par exemple, dans la première colonne, la description concernant la dernière image est « A herd of elephants walking across a dry grass field » (« Un troupeau d’éléphants marchant à travers un champ d’herbe sèche »), ce qui est très bien précisé. Ensuite, dans la deuxième colonne, la première image donne « Two dogs play in the grass » (« Deux chiens jouent dans l’herbe »), alors qu’il s’agit en fait de trois chiens. Dans la dernière colonne, on trouve les exemples les plus erronés comme « A yellow school bus parked in a parking lot » (« Un bus scolaire jaune garé dans un parking »). En général, ces résultats montrent que ce réseau peut échouer de manière assez radicale et être parfois performant. C’est le cas d’un vecteur d’entrée, qui est la représentation d’une image, à une séquence de symboles, qui sont par exemple des caractères ou des mots composant les phrases. Ce type d’architecture est appelé un réseau autorégressif. Un réseau autorégressif est un réseau qui donne une sortie lorsque vous alimentez comme entrée la sortie précédente.

Figure 6 : Exemple de vec2seq où on génère un texte à partir d’une image

Le second type est le « sequence to vector ». Ce réseau continue de donner une séquence de symboles et renvoie à la fin qu’une sortie finale. Une application de ce type peut être l’utilisation d’un réseau pour interpréter Python. Par exemple, les entrées sont ces lignes du programme Python.

Figure 7 : Seq to Vec

Figure 8 : Lignes d'entrée des codes Python

Le réseau est alors en mesure de produire la solution correcte de ce programme. Un autre programme plus compliqué :

Figure 9 : Lignes d'entrée des codes Python dans un cas plus compliqué

La sortie devrait être 12184. Ces deux exemples montrent que l’on peut entraîner un réseau de neurones à effectuer ce genre d’opération. Il suffit de donner une séquence de symboles et de faire en sorte que la sortie finale soit une valeur spécifique.

Le troisième cas est « sequence to vector to sequence », comme le montre la figure 10. Cette architecture était autrefois la méthode standard pour effectuer les traductions linguistiques. On commence par une séquence de symboles illustrée ici en rose. Ensuite, tout est condensé dans ce $h$ final qui représente un concept. Par exemple, nous pouvons avoir une phrase comme entrée et la comprimer temporairement dans un vecteur, qui représente le sens et le message à transmettre. Ensuite, après avoir obtenu ce sens dans n’importe quelle représentation, le réseau le déroule dans une autre langue. Par exemple, « Today I’m very happy » dans une séquence de mots en anglais peut être traduit en italien ou en chinois. En général, le réseau reçoit une sorte d’encodage en entrée et le transforme en une représentation compressée. Enfin, il effectue le décodage en donnant la même version compressée. Les transformers surpassent cette méthode dans les tâches de traduction. Ce type d’architecture était encore à la pointe de la technologie il y a environ deux ans (2018).

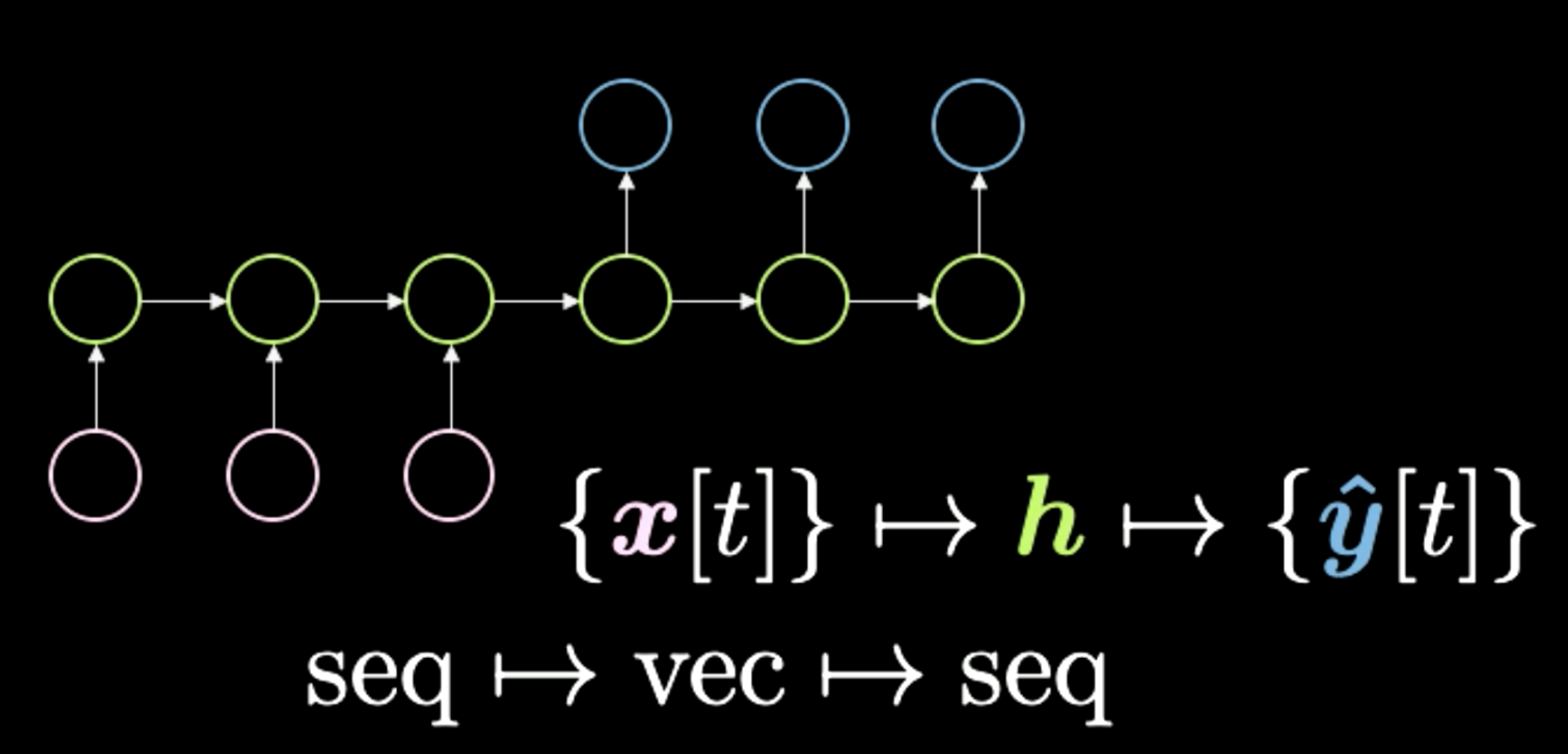
Figure 10 : Seq to Vec to Seq

Si l’on effectue une ACP sur l’espace latent, on obtient les mots regroupés par sémantique comme indiqué dans ce graphique :

Figure 11 : Mots groupés par sémantique après une ACP

Si nous faisons un zoom sur la figure 11, nous pouvons voir par exemple que les mois de l’année sont regroupés au même endroit :

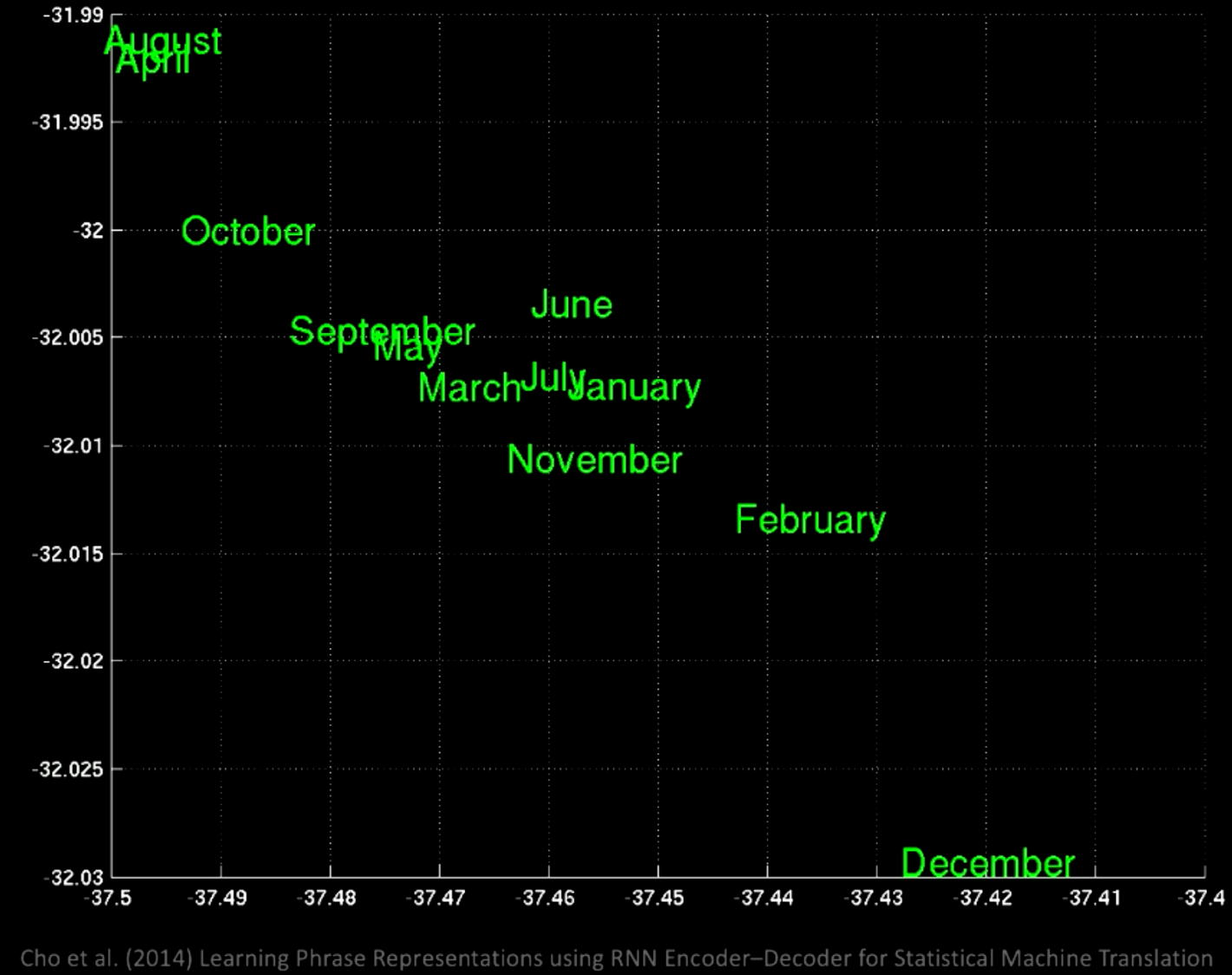
Figure 12 : Zoom sur les groupes de mots

En se concentrant sur une autre région, on obtient des regroupements de phrases comme « il y a quelques jours », « les prochains mois », etc.

Figure 13 : Groupes de mots dans une autre région

Ces exemples montrent que les différents lieux ont des significations communes spécifiques.

La figure 14 montre comment l’entraînement de ce type de réseau permet de saisir certaines caractéristiques sémantiques. Par exemple, dans ce cas, il y a un vecteur reliant « man » à « woman » et un autre entre « king » et « queen ». Cela signifie que « woman » - « man » = « queen » et « king ». On obtient la même distance dans cet espace d’enchâssement pour des cas comme homme-femme. Il est possible d’appliquer ce type de transformation linéaire pour passer d’une conjugaison à une autre ou d’un pays à une capitale.

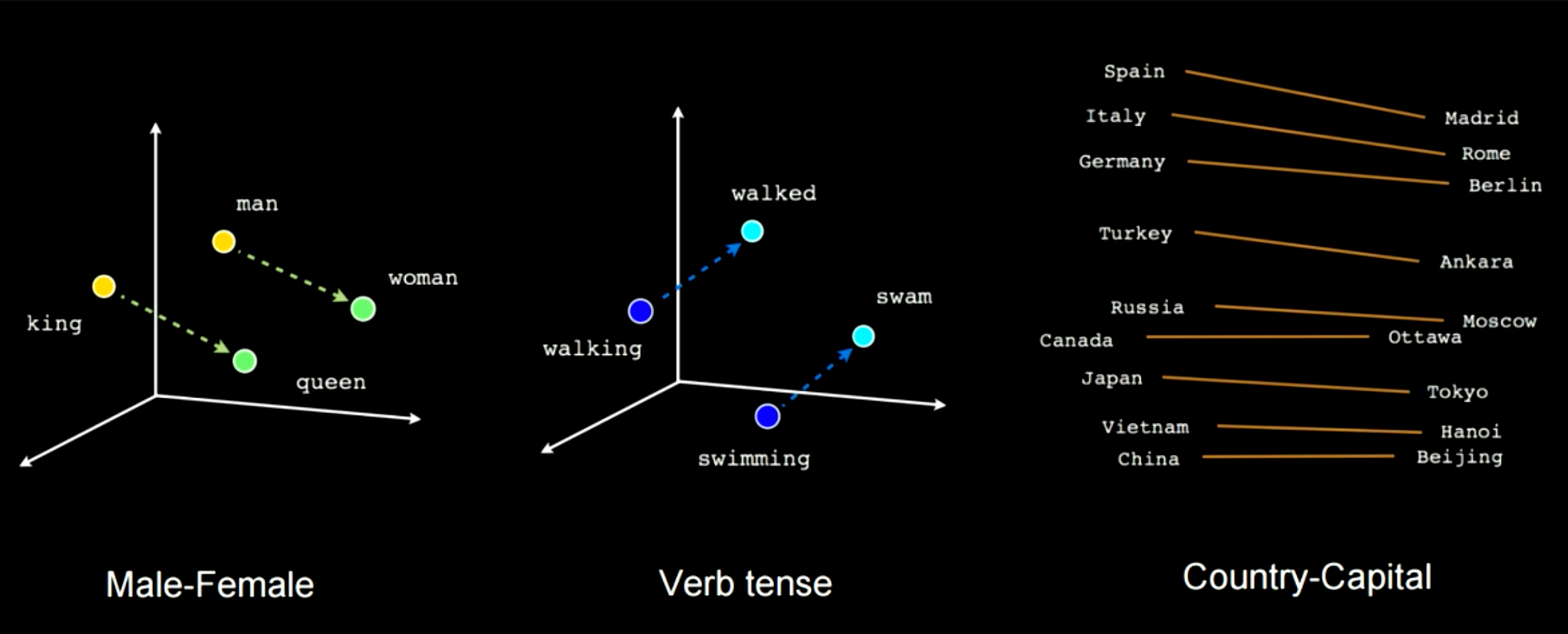
Figure 14 : Caractéristiques sémantiques choisies pendant l’entraînement

Le quatrième et dernier cas est celui du « sequence to sequence ». Dans ce type de réseau, lorsque on commence à donner les entrées, le réseau commence à générer des sorties. Un exemple est le T9, qui était présent sur les téléphones Nokia. Il fournissait des suggestions de texte pendant que l’on écrivait. Un autre exemple est la génération de sous-titre depuis la voix.

Figure 15 : Séquence à Séquence

Un exemple intéressant est ce « RNN écrivain ». En commençant notre phrase par « Les anneaux de Saturne scintillent pendant que », le réseau suggère « deux hommes se regardent ». Ce réseau a été entraîné sur certains romans de science-fiction. Un autre exemple est présenté à la figure 16. La phrase saisie est celle en haut. Le réseau (GPT-2) complète le reste.

Figure 16 : Modèle d'autogénération de texte

Rétropropagation à travers le temps

Architecture

Pour entraîner un RNN, il faut utiliser la rétropropagation à travers le temps. L’architecture du RNN est donnée dans la figure ci-dessous. Le modèle de gauche utilise la représentation pliée tandis que le modèle de droite déplie la boucle en une ligne au fil du temps.

Figure 17 : Rétropropagation à travers le temps

Les représentations cachées sont indiquées comme suit :

La première équation indique une fonction non linéaire appliquée à une rotation d’une version empilée de l’entrée où la configuration précédente de la couche cachée est ajoutée. Au début, $h[0]$ est mis à 0. Pour simplifier l’équation, $W_h$ peut être écrit sous forme de deux matrices séparées, $\left[ W_{hx}\ W_{hh}\right]$, ainsi parfois la transformation peut être énoncée comme

qui correspond à la représentation empilée de l’entrée.

$y[t]$ est calculée à la rotation finale et nous pouvons alors utiliser la règle de la chaîne pour rétropropager l’erreur au pas de temps précédent.

Batch-ification en modélisation du langage

Lorsqu’il s’agit d’une séquence de symboles, nous pouvons regrouper le texte en différentes tailles. Par exemple, lorsqu’il s’agit des séquences illustrées dans la figure suivante, la batch-ification peut être appliquée lorsque le domaine temporel est préservé verticalement. Dans ce cas, la taille du batch est fixée à 4.

Figure 18 : Batch-ification

Si la période $T$ de la rétropropagation à travers le temps est fixée à 3, la première entrée $x[1:T]$ et la sortie $y[1:T]$ pour RNN est déterminée comme

Lors de l’exécution du RNN sur le premier batch, nous introduisons d’abord $x[1] = [a [g [m] s]$ dans le réseau et forçons la sortie à être $y[1] = [b [h [n] t]$. La représentation cachée $h[1]$ est envoyée au prochain pas de temps pour aider le RNN à prédire $y[2]$ à partir de $x[2]$. Après avoir envoyé $h[T-1]$ à l’ensemble final de $x[T]$ et $y[T]$, nous coupons le processus de propagation des gradients pour $h[T]$ et $h[0]$ afin que les gradients ne se propagent pas à l’infini (.detach() en Pytorch). L’ensemble du processus est illustré dans la figure ci-dessous.

Figure 19 : Batch-ification

Disparition et explosion du gradient

Problème

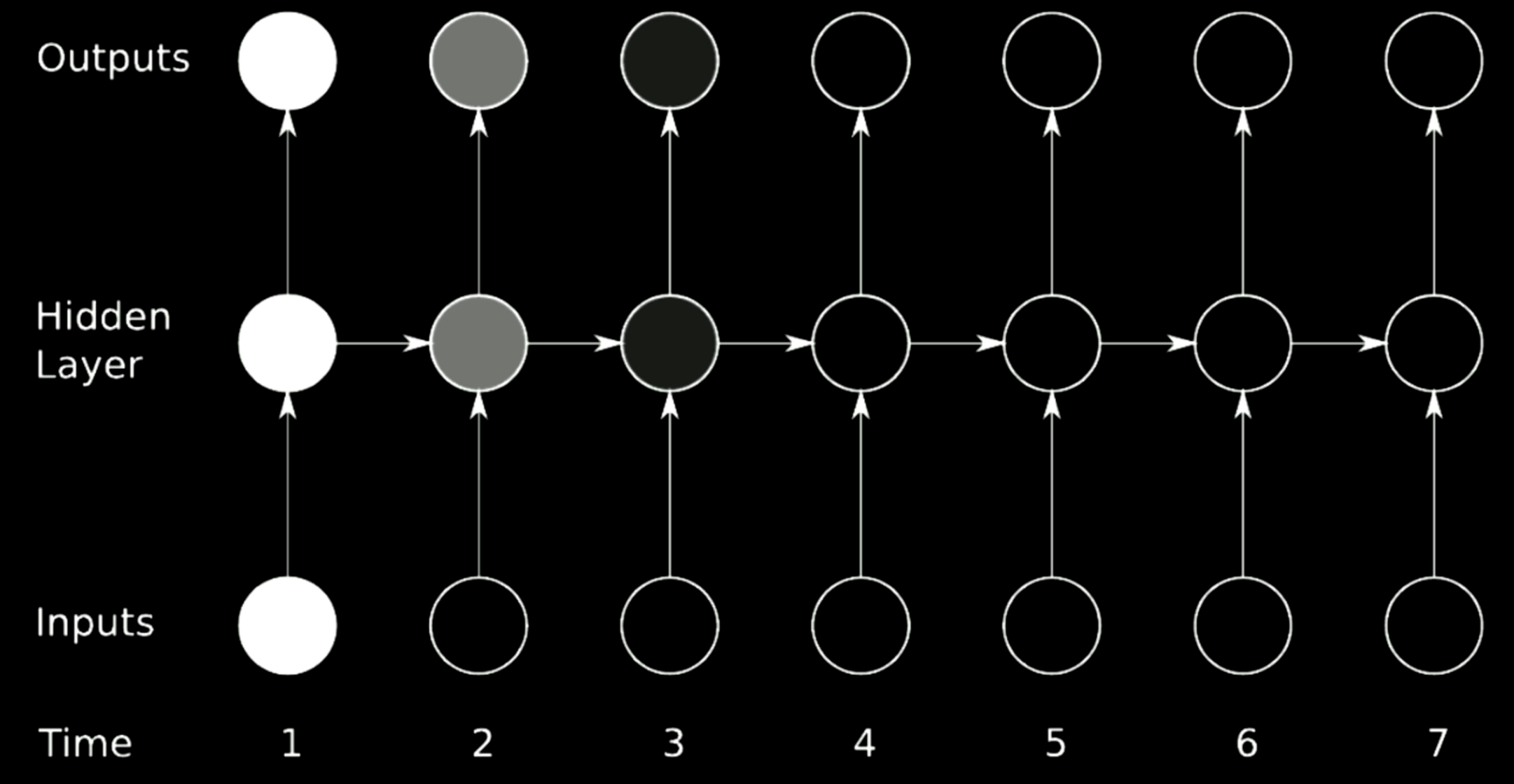
Figure 20 : Problème de la disparition du gradient

La figure ci-dessus est une architecture RNN standard. Afin d’effectuer une rotation sur les étapes précédentes du RNN, nous utilisons des matrices qui peuvent être considérées comme des flèches horizontales dans la figure ci-dessus. Comme les matrices peuvent modifier la taille des sorties, si le déterminant que nous sélectionnons est supérieur à 1, le gradient gonflera au fil du temps et provoquera une explosion du gradient. Mathématiquement parlant, si la valeur propre que nous sélectionnons est petite par rapport à 0, le processus de propagation réduira les gradients et entraînera la disparition du gradient.

Dans les RNNs standards, les gradients se propagent à travers toutes les flèches possibles, ce qui leur donne une grande chance de disparaître ou d’exploser. Par exemple, le gradient au temps 1 est grand, ce qui est indiqué par la couleur vive. Lorsqu’il effectue une rotation, le gradient rétrécit beaucoup et au temps 3, il a disparu.

Solution

L’idéal pour éviter que les gradients n’explosent ou ne disparaissent est de sauter des connexions. Pour y parvenir, on peut utiliser des réseaux de multiplication.

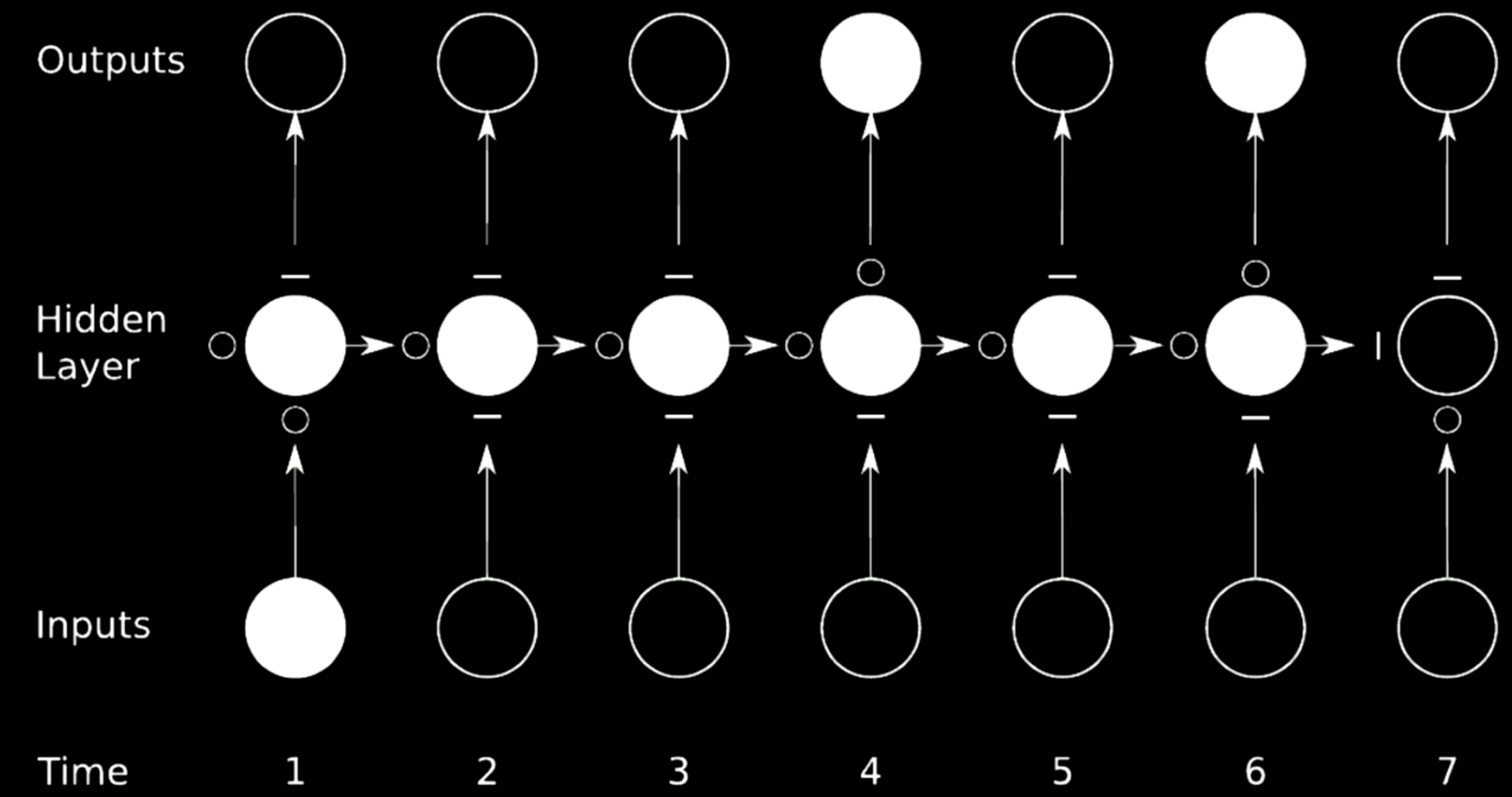
Figure 21 : Sauter des connexions

Dans le cas ci-dessus, nous avons divisé le réseau initial en 4 réseaux. Prenons le premier réseau par exemple. Il prend une valeur de l’entrée au temps 1 et envoie la sortie au premier état intermédiaire de la couche cachée. L’état a 3 autres réseaux où le $\circ$ permet aux gradients de passer tandis que le $-$ bloque la propagation. Une telle technique est appelée réseau récurrent à portes.

Une LSTM est un RNN à portes et est présentée en détail dans les sections suivantes.

Long Short-Term Memory

Architecture des LSTMs

Les équations expliquant une LSTM sont visibles dans la figure 22. La porte d’entrée est représentée par des cases jaunes, et sont une transformation affine. Cette transformation d’entrée multiplie $c[t]$, qui est notre porte candidate.

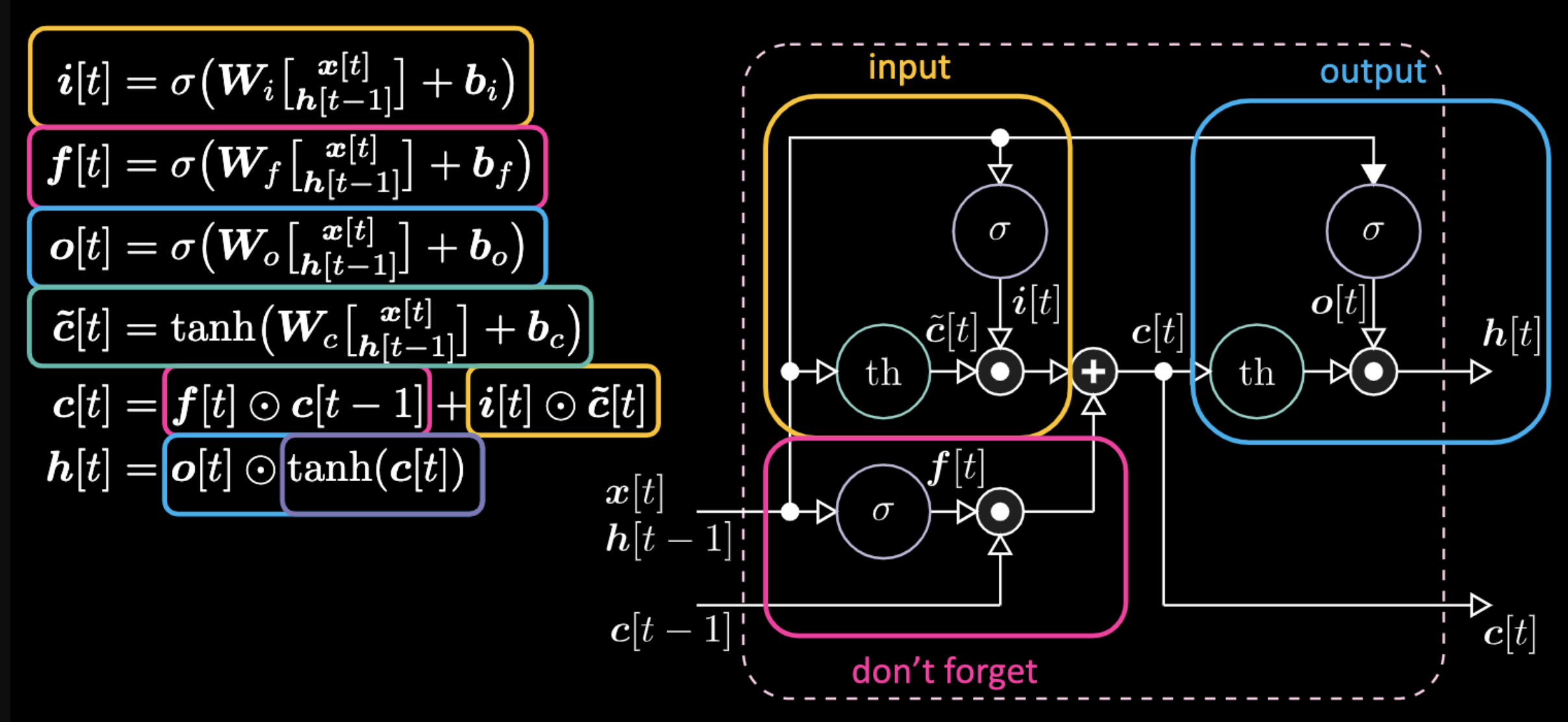
Figure 22 : Architecture d’un réseau LSTM

La « Don’t forget gate » sur le graphique multiplie la valeur précédente de la cellule mémoire $c[t-1]$. La valeur totale de la cellule $c[t]$ est égale à la somme de la « Don’t forget gate» et de l’« Input gate ». La représentation cachée finale est une multiplication par élément entre la porte de sortie $o[t]$ et la version tangente hyperbolique de la cellule $c[t]$, de sorte que les valeurs soient limitées. Enfin, la porte candidate $\tilde{c}[t]$ est simplement un réseau récurrent. Nous avons donc un $o[t]$ pour moduler la sortie, un $f[t]$ pour moduler la porte « don’t forget », et un $i[t]$ pour moduler la porte d’entrée. Toutes ces interactions entre la mémoire et les portes sont des interactions multiplicatives. $i[t]$, $f[t]$ et $o[t]$ sont tous des sigmoïdes, allant de 0 à 1. Par conséquent, en multipliant par 0, vous obtenez une porte fermée. En multipliant par 1, vous avez une porte ouverte.

Comment éteindre la sortie ? Supposons que nous ayons une représentation interne violette $th$ et que nous mettions un 0 dans la porte de sortie. La sortie sera alors 0 multiplié par quelque chose ce qui donne 0. Si nous mettons un 1 dans la porte de sortie, nous obtenons la même valeur que la représentation en violet.

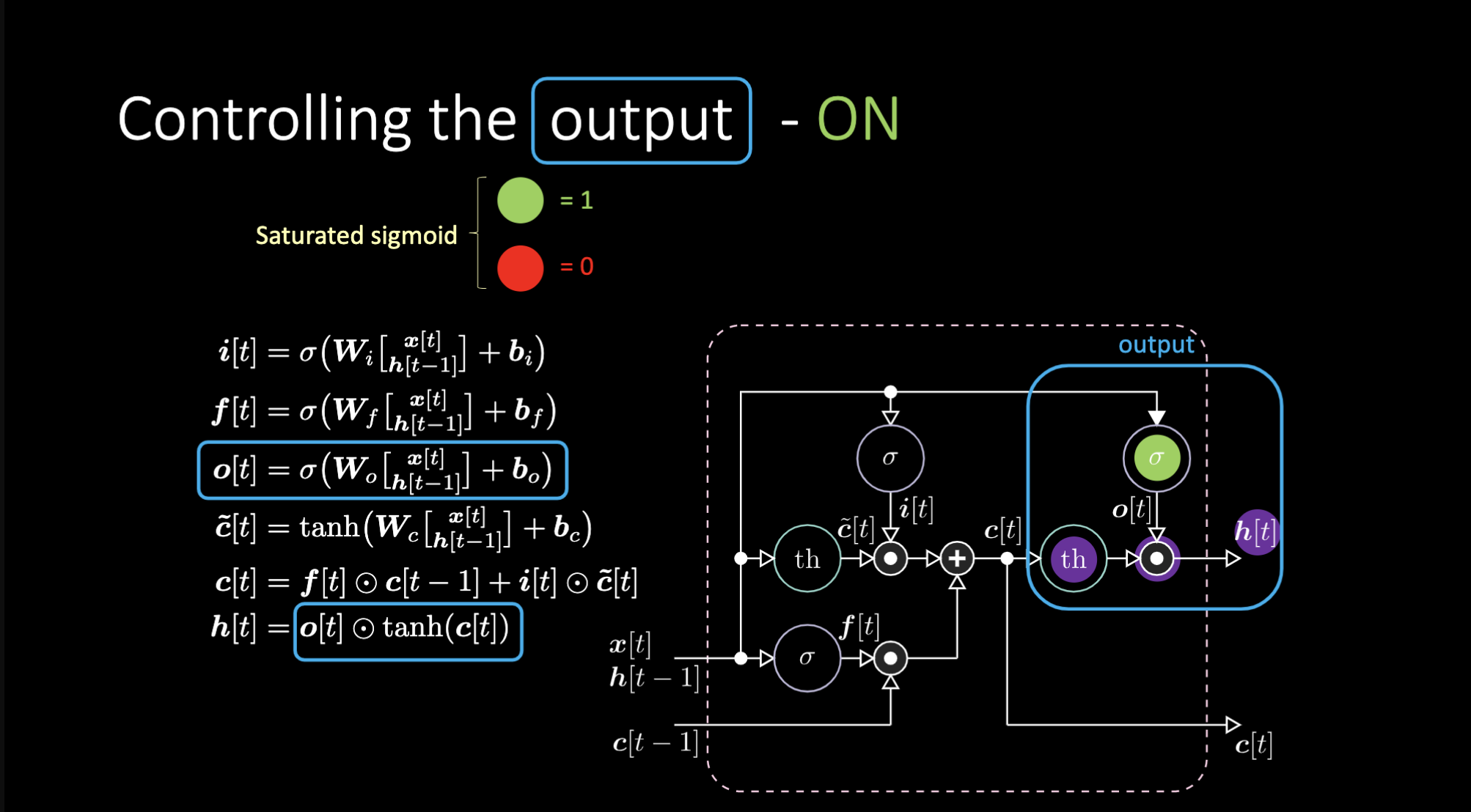
Figure 23 : Architecture LSTM - Sortie activée

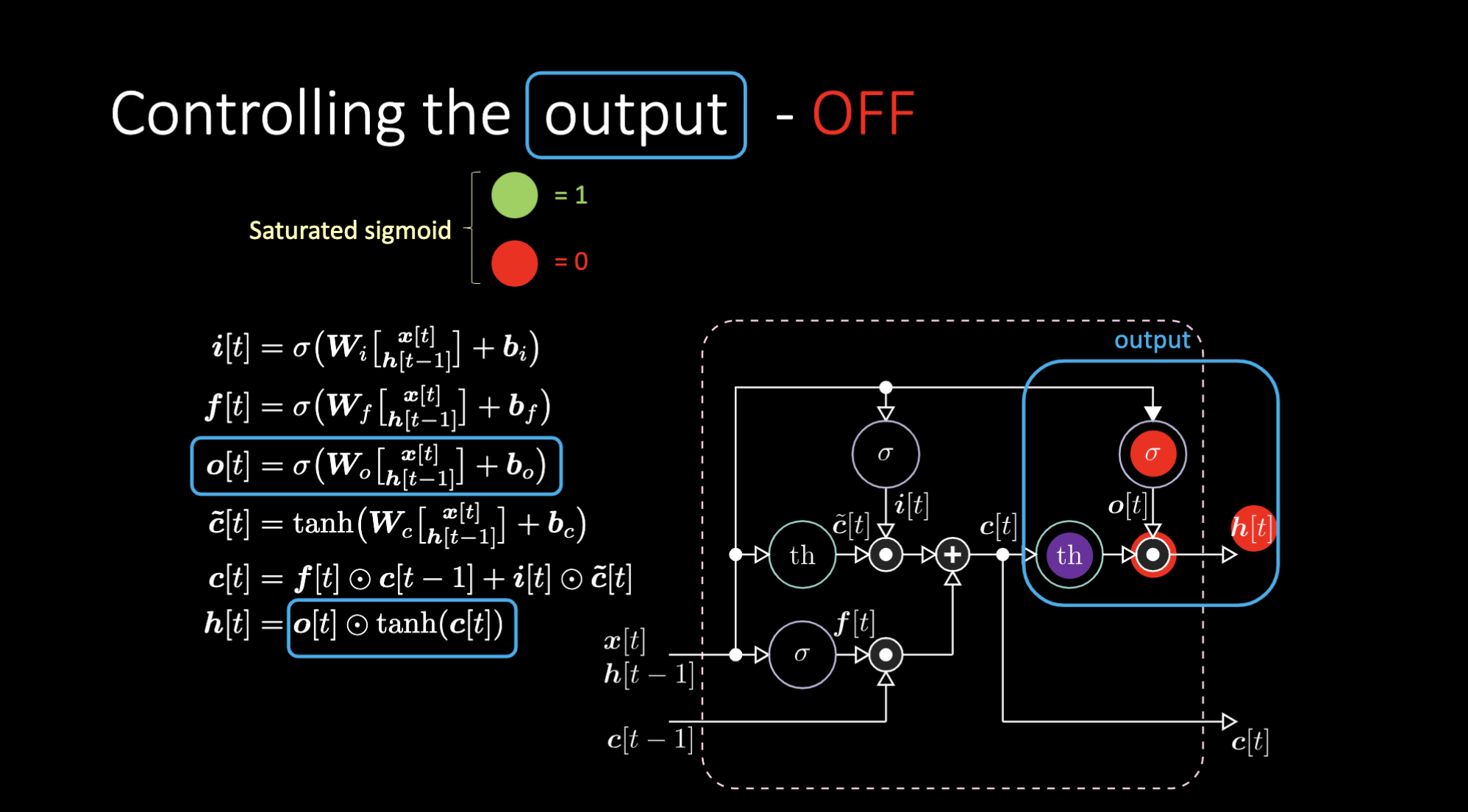
Figure 24 : Architecture LSTM - Sortie désactivée

De même, nous pouvons contrôler la mémoire. Par exemple, nous pouvons la réinitialiser en faisant en sorte que $f[t]$ et $i[t]$ soient des 0. Après multiplication et sommation, nous avons un 0 dans la mémoire. Sinon, nous pouvons conserver la mémoire, en mettant toujours à 0 la représentation interne $th$ mais en gardant un 1 dans $f[t]$. Ainsi, la somme obtient $c[t-1]$ et continue à l’envoyer. Enfin, nous pouvons écrire de manière à obtenir un 1 dans la porte d’entrée, la multiplication devient violette, puis mettre un 0 dans la porte « don’t forget » pour qu’elle oublie réellement.

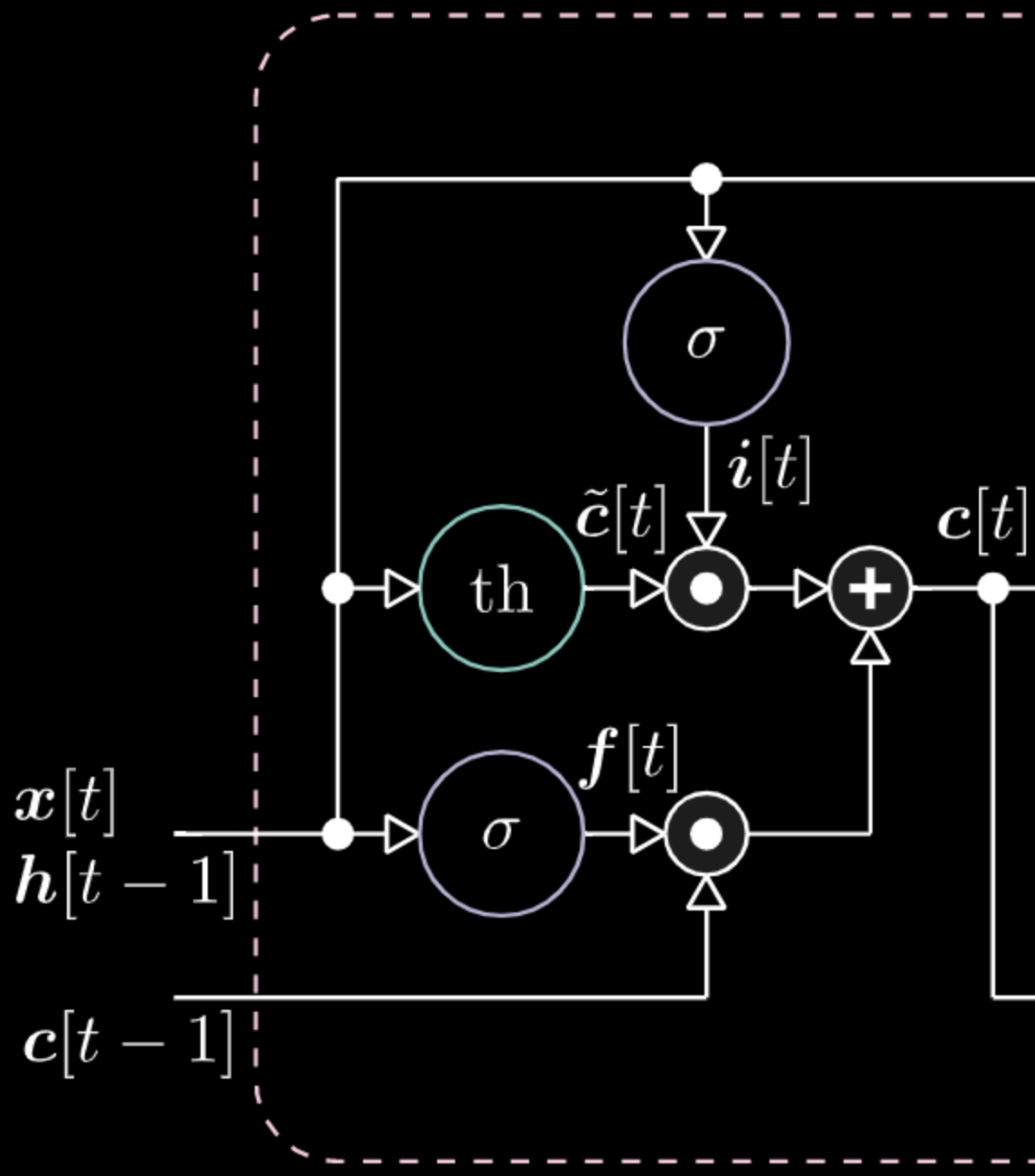
Figure 25 : Visualisation de la cellule mémoire

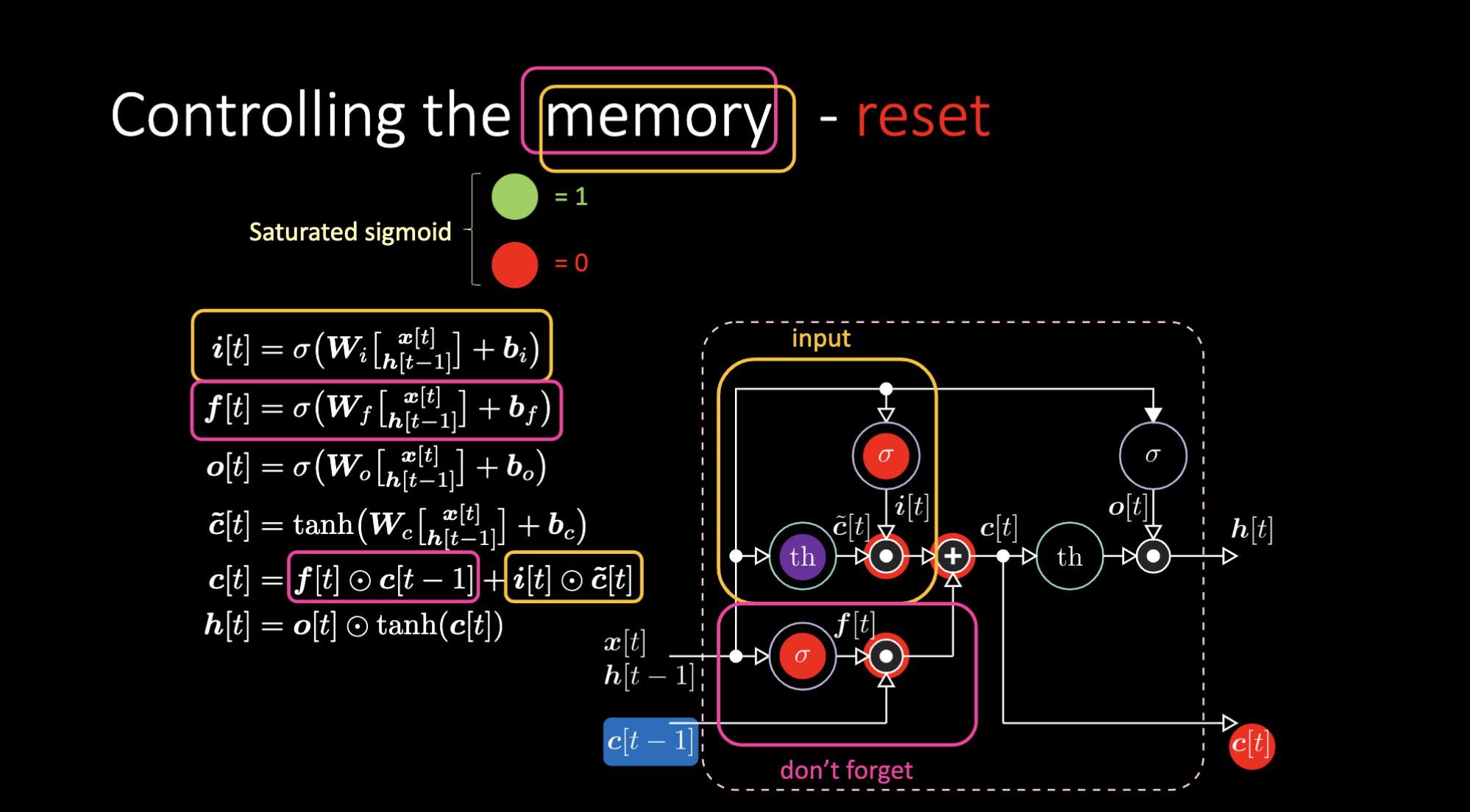
Figure 26 : Architecture LSTM - Réinitialisation de la mémoire

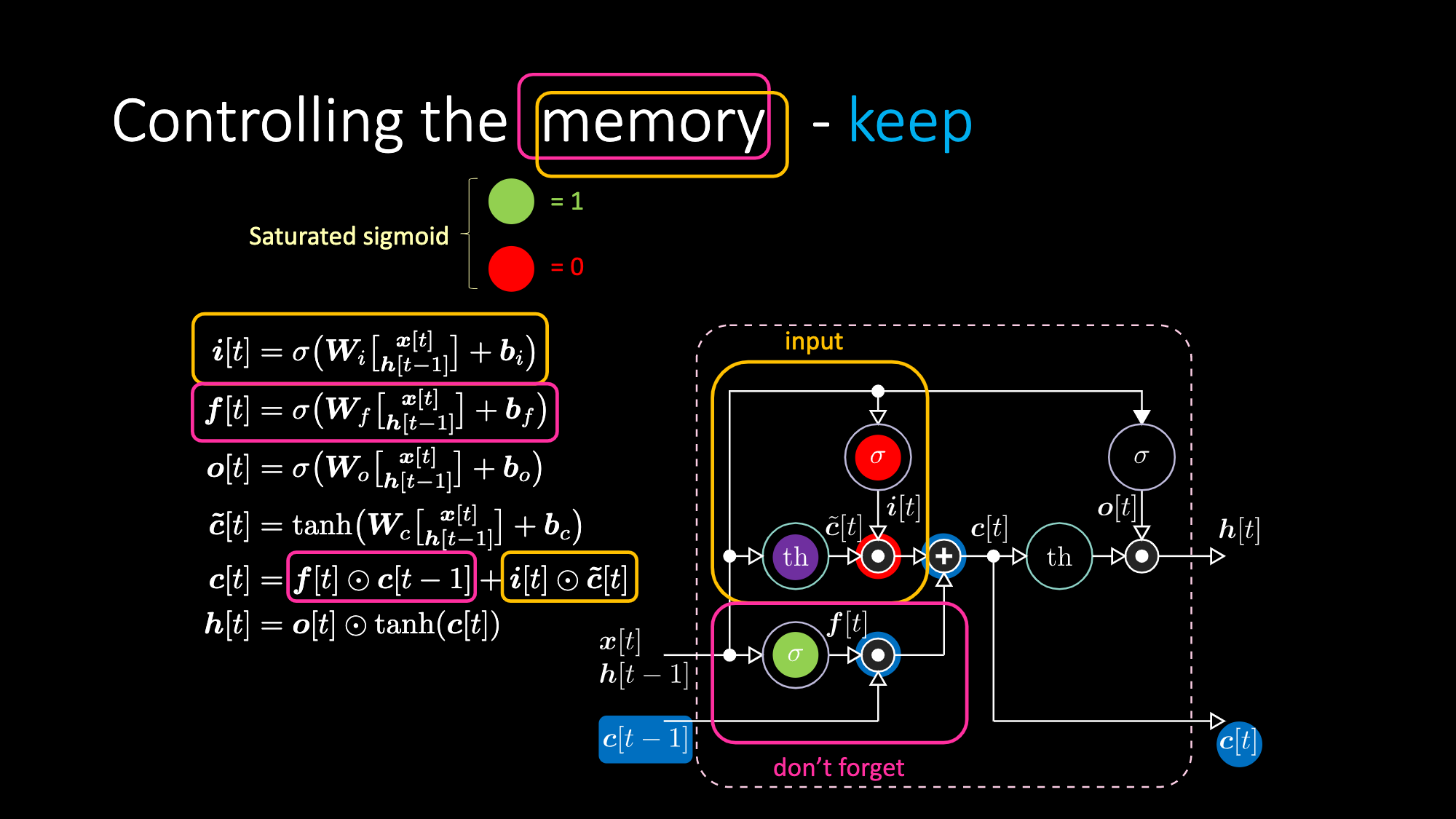
Figure 27 : Architecture STM - Conserver la mémoire

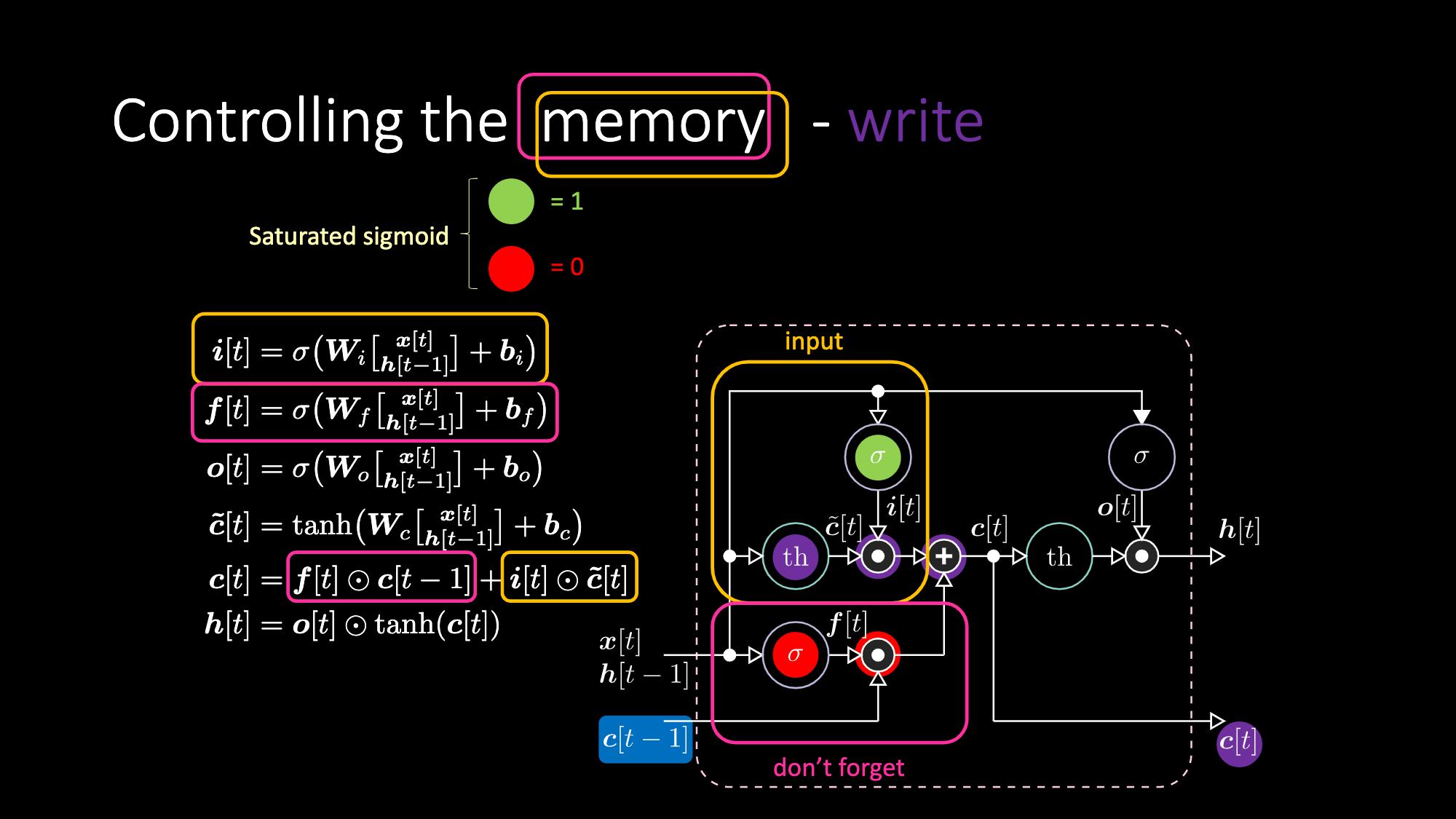
Figure 28 : Architecture LSTM - Mémoire d'écriture

Exemples

Classification des séquences

Cette section se réfère au code du notebook Jupyter trouvable ici pour la version en anglais et ici pour la version en français. L’objectif est de classer les séquences. Les éléments et les cibles sont représentés localement (vecteurs d’entrée avec un seul bit non nul). La séquence commence par un B (pour begins en anglais), se termine par un E (pour ends en anglais) qui le symbole déclencheur. Sinon la séquence est constituée de symboles choisis au hasard dans l’ensemble {a, b, c, d}, à l’exception de deux éléments aux positions $t_1$ et $t_2$ qui sont soit X soit Y. Dans le cas du DifficultyLevel.HARD, la longueur de la séquence est choisie au hasard entre 100 et 110, $t_1$ est choisi au hasard entre 10 et 20, et $t_2$ est choisi au hasard entre 50 et 60. Il y a 4 classes de séquence Q, R, S, et U, qui dépendent de l’ordre temporel de X et Y. Les règles sont les suivantes : X, X -> Q; X, Y -> R; Y, X -> S; Y, Y -> U.

1) Exploration du jeu de données

Le type retourné par un générateur de données est un tuple de longueur 2. Le premier élément du tuple est le batch de séquences de forme $(32, 9, 8)$. Ce sont les données qui vont être introduites dans le réseau. Il y a huit symboles différents dans chaque ligne (X, Y, a, b, c, d, B, E). Chaque ligne est un vecteur one-hot. Une séquence de lignes représente une séquence de symboles. La première ligne entièrement nulle est un rembourrage. Nous utilisons le rembourrage lorsque la longueur de la séquence est plus courte que la longueur maximale du batch. Le deuxième élément du tuple est le batch correspondant aux labels des classes de forme $(32, 4)$, puisque nous avons 4 classes (Q, R, S, et U). La première séquence est : BbXcXcbE. Ensuite, son label décodé est $[1, 0, 0, 0]$, ce qui correspond à Q.

Figure 29 : Exemple de vecteur d'entrée

2) Définition du modèle et entraînement

Créons un simple réseau récurrent, une LSTM, et entraînons-les sur 10 époques. Dans la boucle d’entraînement, nous devons toujours regarder cinq étapes :

• Effectuer la passe en avant du modèle
• Calculer la perte
• Remettre à zéro le cache des gradients
• Rétropropager pour calculer la dérivée partielle de la perte en fonction des paramètres
• Aller dans le sens inverse du gradient

Figure 30 : RNN simple (en haut) vs LSTM (en bas)- 10 époques

Avec un niveau de difficulté facile, RNN obtient une précision de 50% tandis que LSTM obtient 100% après 10 époques. Mais la LSTM a quatre fois plus de poids que le RNN et possède deux couches cachées, ce qui ne permet pas une comparaison équitable. Après 100 époques, le RNN obtient également une précision de 100 %, ce qui prend plus de temps que la LSTM pour s’entraîner.

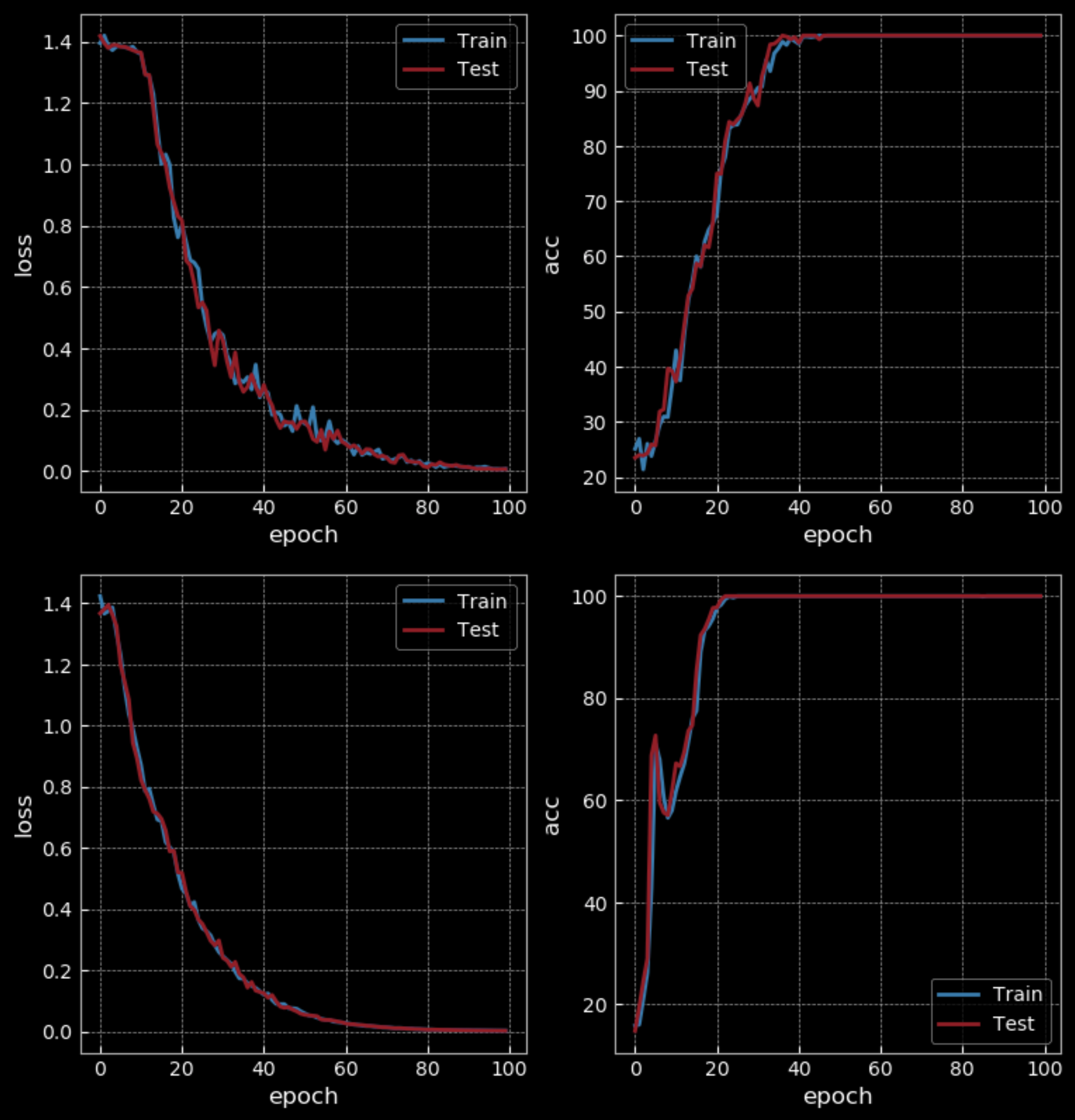
Figure 31 : RNN simple (en haut) vs LSTM (en bas) - 100 époques

Si nous augmentons la difficulté de l’entraînement (en utilisant des séquences plus longues), le RNN échouera alors que la LSTM continuera de fonctionner.

Figure 32 : Visualisation de la valeur cachée de l'État

La visualisation ci-dessus donne la valeur de l’état caché au fil du temps dans la LSTM. Nous passons les entrées dans une tangente hyperbolique, de sorte que si l’entrée est inférieure à $-2,5$, elle sera mise en correspondance avec $-1$ et si elle est supérieure à $2,5$, elle sera mise en correspondance avec $1$. Dans ce cas, nous pouvons donc voir la couche cachée spécifique choisie sur X (cinquième ligne de l’image), qui devient rouge jusqu’à ce que nous obtenions l’autre X. Ainsi, la cinquième unité cachée de la cellule est déclenchée par l’observation du X et se calme après avoir vu l’autre X. Cela nous permet de reconnaître la classe de la séquence.

L’écho du signal

Cette section se réfère au code du notebook Jupyter trouvable ici pour la version en anglais et ici pour la version en français. L’écho du signal n étapes est un exemple de tâche synchronisée de plusieurs à plusieurs. Par exemple, la 1ère séquence d’entrée est 1 1 0 0 1 0 1 1 0 0 0 0 0 0 0 0 0 1 1 1 1 ..., et la 1ère séquence cible est 0 0 0 1 1 0 0 1 0 1 1 0 0 0 0 0 0 0 0 0 0 1 .... Dans ce cas, la sortie se fait trois étapes plus tard. Nous avons donc besoin d’une mémoire de travail de courte durée pour conserver les informations. Alors que dans le modèle linguistique, cela revient à dire quelque chose qui n’a pas encore été dit.

Avant d’envoyer la séquence complète au réseau et de forcer la cible finale à être quelque chose, nous devons couper la longue séquence en petits morceaux. Tout en alimentant un nouveau morceau, nous devons garder une trace de l’état caché et l’envoyer comme entrée à l’état interne lors de l’ajout du nouveau morceau suivant. Dans les LSTMs, vous pouvez conserver la mémoire pendant une longue période tant que vous avez une capacité suffisante. Dans les RNNs, une fois que vous avez atteint une certaine longueur, la mémoire commence à oublier ce qui s’est passé dans le passé.