RNNs, GRUs, LSTMs, Attention, Seq2Seq, et Réseaux mémoire

Architectures de l’apprentissage profond

En apprentissage profond, il existe différents modules pour réaliser différentes fonctions. L’expertise dans ce domaine implique la conception d’architectures pour réaliser des tâches particulières. L’apprentissage profond réduit une fonction complexe en un graphe de modules fonctionnels (éventuellement dynamiques), dont les fonctions sont finalisées par l’apprentissage.

Comme pour ce que nous avons vu avec les réseaux convolutifs, l’architecture de réseau est importante.

Réseaux récurrents (RNNs)

Dans un ConvNet, le graphe ou les interconnexions entre les modules ne peuvent pas avoir de boucles. Il existe au moins un ordre partiel entre les modules, de sorte que les entrées sont disponibles lorsque nous calculons les sorties.

Comme le montre la figure 1, il existe des boucles dans les réseaux neuronaux récurrents.

Figure 1 : Réseau de neurones récurrent enroulé

• $x(t)$ : entrée qui varie dans le temps
• $\text{Enc}(x(t))$ : encodeur qui génère une représentation de l’entrée
• $h(t)$ : une représentation de l’entrée
• $w$ : paramètres pouvant être entraînés
• $z(t-1)$ : état caché précédent, qui est la sortie du pas de temps précédent
• $z(t)$ : état caché actuel
• $g$ : fonction qui peut être un réseau de neurones compliqué. L’une des entrées est $z(t-1)$ qui est la sortie du pas de temps précédent
• $\text{Dec}(z(t))$ : décodeur qui génère une sortie

Réseaux récurrents dépliés

L’entrée est une séquence $x_1, x_2, \cdots, x_T$.

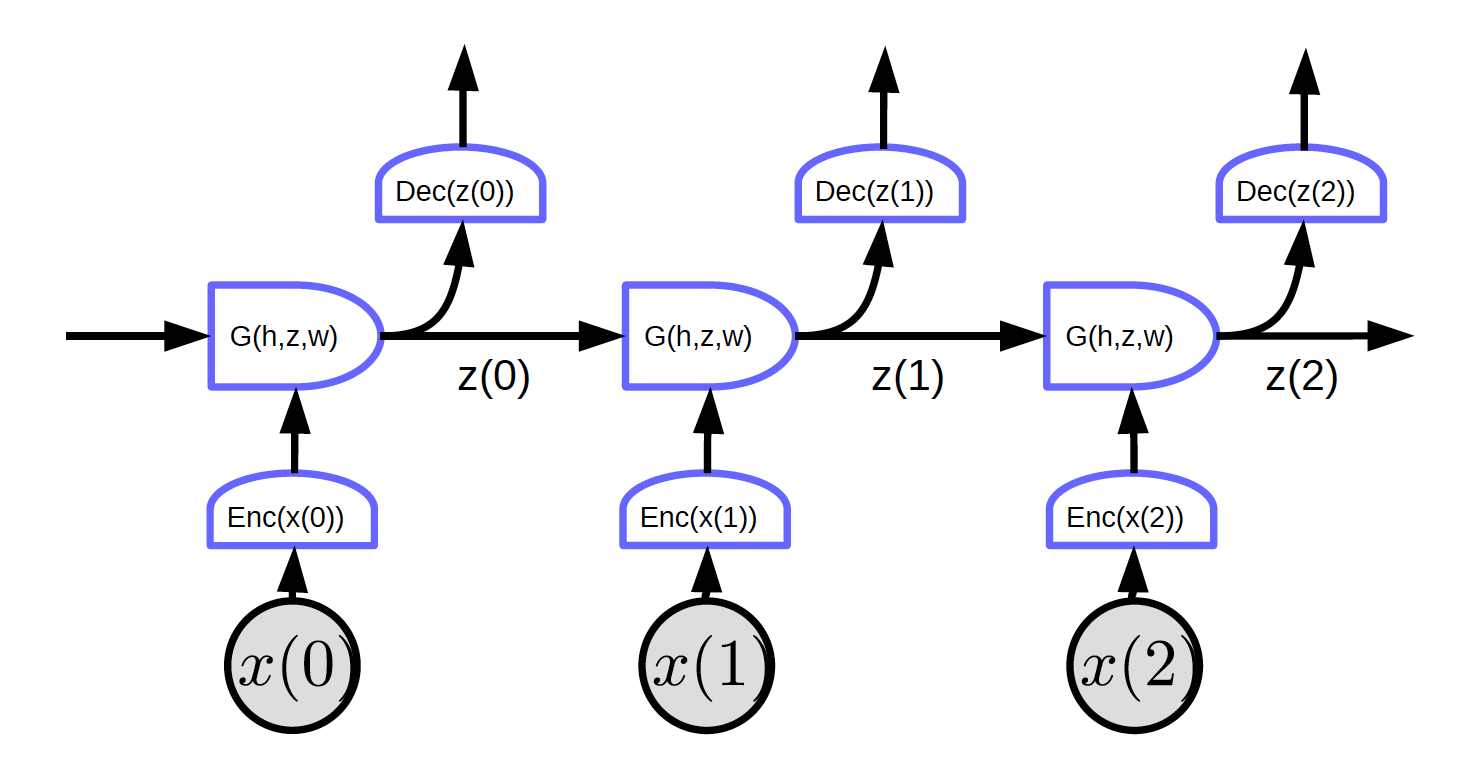
Figure 2 : Réseaux récurrents dépliés

Dans la figure 2, l’entrée est $x_1, x_2, x_3$.

Au temps $t = 0$, l’entrée $x(0)$ est passée à l’encodeur qui génère la représentation $h(x(0)) = \text{Enc}(x(0))$. Puis il la passe à G pour générer l’état caché $z(0) = G(h_0, z’, w)$. À $t = 0$, $z’$ dans $G$ peut être initialisé comme valant $0$ ou de manière aléatoire. $z(0)$ est passé au décodeur pour générer une sortie mais aussi au pas de temps suivant.

Comme il n’y a pas de boucles dans ce réseau nous pouvons mettre en œuvre la rétropropagation.

La figure 2 montre un réseau avec une caractéristique particulière : chaque bloc partage les mêmes poids. Trois encodeurs, décodeurs et fonctions G ont respectivement les mêmes poids sur différents pas de temps.

Malheureusement, la rétropropagation à travers le temps (BPTT pour Backpropagation through time) ne fonctionne pas aussi bien dans la forme naïve du RNN.

Il existe des problèmes avec les RNNs :

1. La disparition du gradient
   • Dans une longue séquence, les gradients sont multipliés par la matrice de poids (transposée) à chaque pas de temps. S’il y a de petites valeurs dans la matrice de poids, la norme des gradients devient de plus en plus petite de manière exponentielle.
2. L’explosion du gradient
   • Si nous avons une grande matrice de poids et que la non-linéarité dans la couche récurrente n’est pas saturée, les gradients vont exploser. Les poids divergeront à l’étape de mise à jour. Il se peut que nous devions utiliser un taux d’apprentissage minuscule pour que la descente des gradients fonctionne.

L’une des raisons d’utiliser les RNNs est l’avantage de pouvoir se souvenir des informations du passé. Cependant, cette mémoire peut être limitée.

Un exemple étant le problème de la disparition des gradients. Considérons une entrée constituée des caractères d’un programme en langage C. Le système doit indiquer s’il s’agit d’un programme syntaxiquement correct. Un programme syntaxiquement correct doit avoir un nombre valide d’accolades et de parenthèses. Ainsi, le réseau doit se souvenir du nombre de parenthèses et d’accolades ouvertes à vérifier et si elles sont bien toutes fermées. Le réseau doit stocker ces informations dans des états cachés comme un compteur. Cependant, en raison de la disparition des gradients, il ne parviendra pas à conserver ces informations dans un long programme.

Astuces pour les RNNs

• On peut couper les gradients pour éviter l’explosion, les écraser lorsqu’ils deviennent trop importants.
• On peut jouer sur l’initialisation (commencer à droite évite l’explosion/la disparition). Initialiser les matrices de poids pour préserver la norme dans une certaine mesure. Par exemple, l’initialisation orthogonale initialise la matrice de poids comme une matrice orthogonale aléatoire.

Modules multiplicatifs

Dans les modules multiplicatifs, plutôt que de calculer uniquement une somme pondérée d’entrées, nous calculons les produits des entrées et nous calculons ensuite la somme pondérée de celles-ci.

Supposons $x \in {R}^{n\times1}$, $W \in {R}^{m \times n}$, $U \in {R}^{m \times n \times d}$ et $z \in {R}^{d\times1}$. Ici, U est un tenseur.

où $s_i = w_{i}^\top x = \sum_j w_{ij}x_j$.

La sortie du système est une somme pondérée classique d’entrées et de poids. Les poids eux-mêmes sont également des sommes pondérées de poids et d’entrées.

Architecture d’hyper-réseau : les poids sont calculés par un autre réseau.

L’attention

$x_1$ et $x_2$ sont des vecteurs, $w_1$ et $w_2$ sont des scalaires après softmax où $w_1 + w_2 = 1$, et $w_1$ et $w_2$ sont compris entre 0 et 1.

$w_1x_1 + w_2x_2$ est une somme pondérée de $x_1$ et $x_2$ pondérée par les coefficients $w_1$ et $w_2$.

En modifiant la taille relative de $w_1$ et $w_2$, nous pouvons faire passer la sortie de $w_1x_1 + w_2x_2$ à $x_1$ ou $x_2$ ou à certaines combinaisons linéaires de $x_1$ et $x_2$.

Les entrées peuvent avoir plusieurs vecteurs $x$ (plus de $x_1$ et $x_2$). Le système choisira une combinaison appropriée, dont le choix est déterminé par une autre variable $z$. Un mécanisme d’attention permet au réseau neuronal de concentrer son attention sur une ou plusieurs entrées particulières et d’ignorer les autres.

L’attention est de plus en plus importante dans les systèmes de traitement du langage naturel qui utilisent des architectures de type transformers ou d’autres types d’attention (point abordé à la semaine 12).

Les poids sont indépendants des données car $z$ est indépendant des données.

Les Gated Recurrent Units (GRUs)

Comme mentionné ci-dessus, le RNN souffre de la disparition/explosion des gradients et ne se souvient pas des états pendant très longtemps. Les GRUS de Cho et al. (2014), sont une application de modules multiplicatifs qui tente de résoudre ces problèmes. C’est un exemple de réseau récurrent avec mémoire. La structure d’une unité GRU est présentée ci-dessous :

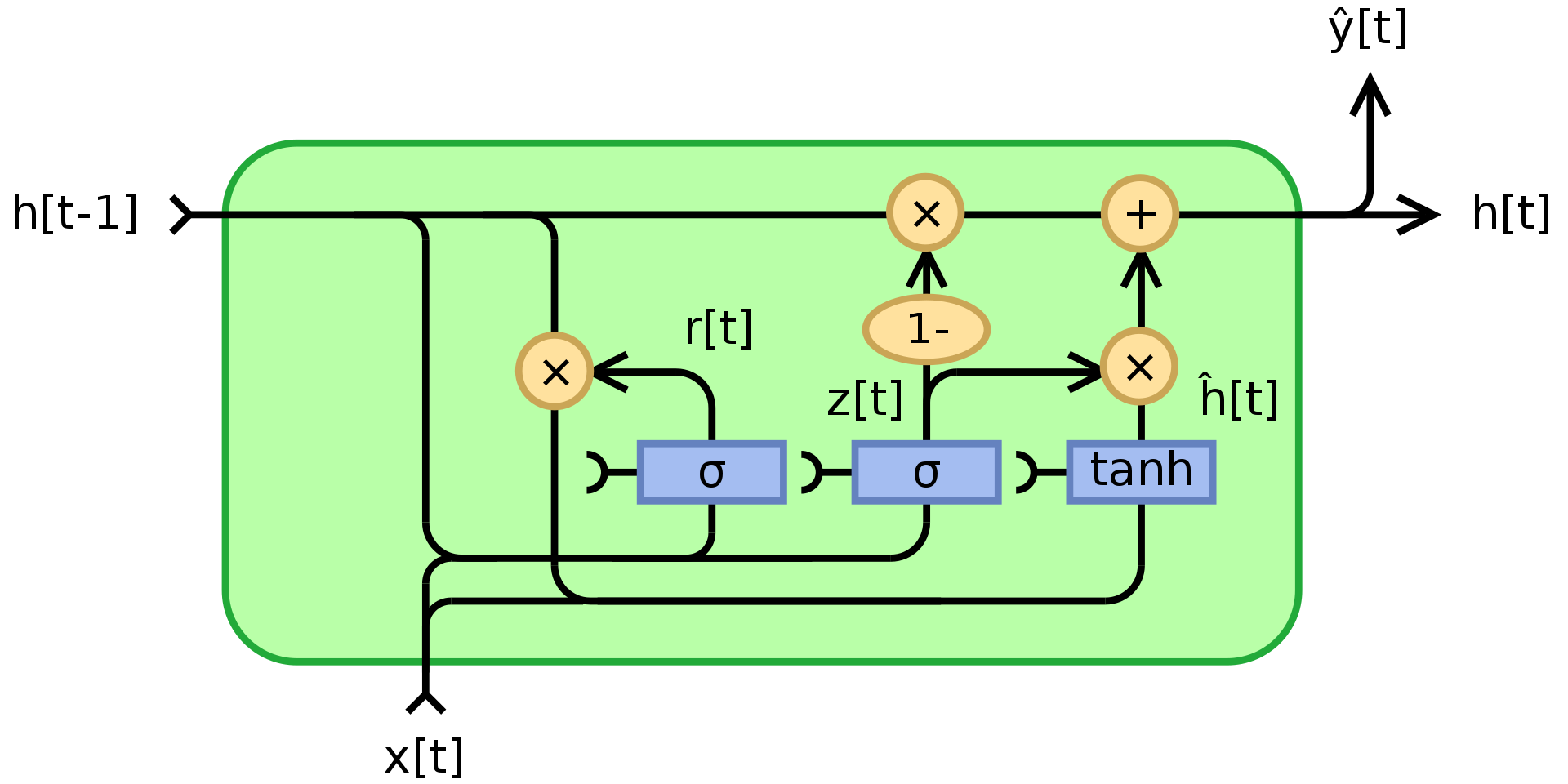
Figure 3 : Gated Recurrent Unit

où $\odot$ indique une multiplication élément par élément (produit Hadamard), $x_t$ est le vecteur d’entrée, $h_t$ est le vecteur de sortie, $z_t$ est le vecteur de mise à jour, $r_t$ est le vecteur de réinitialisation, $\phi_h$ est une tanh, et $W$,$U$,$b$ sont des paramètres pouvant être appris.

Pour être précis, $z_t$ est un vecteur de porte qui détermine quelle part des informations passées doit être transmise dans la suite. Il applique une fonction sigmoïde à la somme de deux couches linéaires et un biais sur l’entrée $x_t$ et l’état précédent $h_{t-1}$.
$z_t$ contient des coefficients entre 0 et 1 résultant de l’application de la fonction sigmoïde. L’état final de sortie $h_t$ est une combinaison convexe de $h_{t-1}$ et de $\phi_h(W_hx_t + U_h(r_t\odot h_{t-1}) + b_h)$ via $z_t$. Si le coefficient est égal à 1, la sortie de l’unité actuelle n’est qu’une copie de l’état précédent et ignore l’entrée (ce qui est le comportement par défaut). S’il est inférieur à 1, il prend en compte de nouvelles informations provenant de l’entrée.

La porte de réinitialisation $r_t$ est utilisée pour décider quelle quantité d’informations passées doit être oubliée. Dans le nouveau contenu de la mémoire $\phi_h(W_hx_t + U_h(r_t\odot h_{t-1}) + b_h)$, si le coefficient dans $r_t$ est 0, alors il ne stocke aucune des informations du passé. Si en plus $z_t$ vaut 0, alors le système est complètement réinitialisé puisque $h_t$ ne regarderait que l’entrée.

Les LSTMs (Long Short-Term Memory)

Les GRUs sont en fait une version simplifiée des LSTMs qui ont été conçues beaucoup plus tôt par Hochreiter et Schmidhuber (1997). En constituant des cellules de mémoire pour préserver les informations passées, les LSTMs visent également à résoudre les problèmes de perte de mémoire à long terme des RNNs. La structure des LSTMs est présentée ci-dessous :

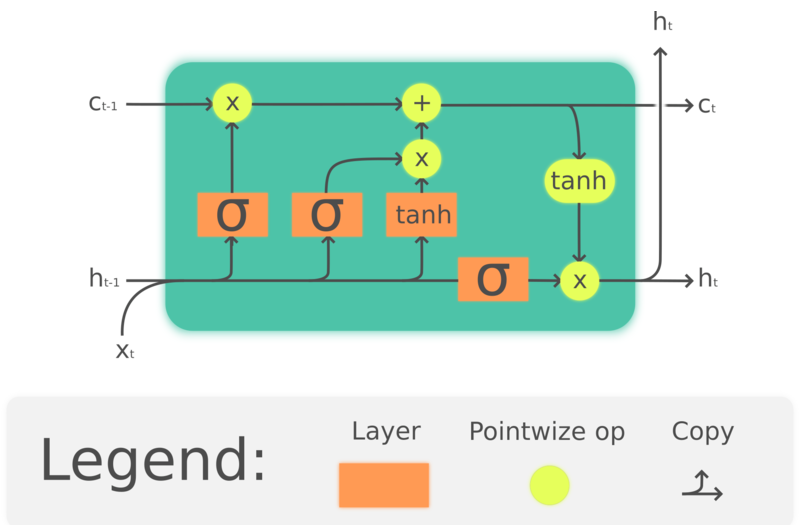
Figure 4 : Long Short-Term Memory

où $\odot$ indique une multiplication élément par élément, $x_t\in\mathbb{R}^a$ est un vecteur d’entrée de l’unité LSTM, $f_t\in\mathbb{R}^h$ est le vecteur d’activation de la porte d’oubli, $i_t\in\mathbb{R}^h$ est le vecteur d’activation de la porte d’entrée/mise à jour, $o_t\in\mathbb{R}^h$ est le vecteur d’activation de la porte de sortie, $h_t\in\mathbb{R}^h$ est le vecteur d’état caché (également appelé sortie), $c_t\in\mathbb{R}^h$ est le vecteur d’état de la cellule.

Une unité LSTM utilise un état de cellule $c_t$ pour transmettre l’information. Elle régule la manière dont l’information est préservée ou retirée de l’état de la cellule par des structures appelées gates (portes). La porte d’oubli $f_t$ décide de la quantité d’informations que nous voulons conserver de l’état de cellule précédent $c_{t-1}$ en regardant l’entrée actuelle et l’état caché précédent. Elle produit un nombre entre 0 et 1 comme coefficient de $c_{t-1}$. $\tanh(W_cx_t + U_ch_{t-1} + b_c)$ calcule un nouveau candidat pour mettre à jour l’état de la cellule. Comme la porte d’oubli, la porte d’entrée $i_t$ décide de la part de mise à jour à appliquer. Enfin, la sortie $h_t$ est basée sur l’état de la cellule $c_t$, mais passe par une $\tanh$ puis est filtrée par la porte de sortie $o_t$.

Bien que les LSTMs soient largement utilisés en traitement du langage naturel, leur popularité est en baisse. Par exemple, la reconnaissance vocale se dirige vers l’utilisation de ConvNets temporels et les autres utilisations se dirigent vers l’utilisation de transformers.

Modèle de séquence à séquence

L’approche proposée par Sutskever (2014) est le premier système de traduction automatique neuronale à avoir des performances comparables aux approches classiques. Elle utilise une architecture d’encodeur-décodeur où l’encodeur et le décodeur sont tous deux des LSTMs multicouches.

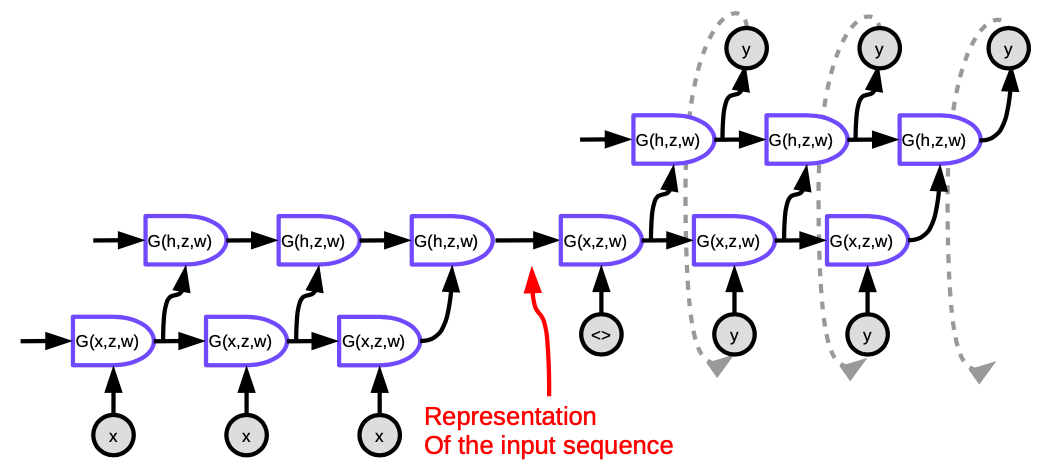
Figure 5 : Seq2Seq

Chaque cellule de la figure est une LSTM. Pour l’encodeur (la partie de gauche), le nombre de pas de temps est égal à la longueur de la phrase à traduire. À chaque pas, il y a une pile de LSTMs (quatre couches dans la publication) où l’état caché de la LSTM précédente est introduit dans le suivante. La dernière couche du dernier pas de temps produit un vecteur qui représente le sens de la phrase entière et est ensuite introduit dans une autre LSTM multicouche (le décodeur) produisant des mots dans la langue cible. Dans le décodeur, le texte est généré de manière séquentielle. Chaque étape produit un mot, qui est introduit dans l’étape de temps suivante.

Cette architecture n’est pas satisfaisante à deux égards. Premièrement, le sens entier de la phrase doit être comprimé dans l’état caché entre l’encodeur et le décodeur. Deuxièmement, les LSTMs ne préservent en fait pas l’information sur plus de 20 mots environ. La solution à ces problèmes est appelée un Bi-LSTM, qui fait fonctionner deux LSTMs dans des directions opposées. Dans un Bi-LSTM, la signification est encodée dans deux vecteurs, l’un généré par l’exécution de la LSTM de gauche à droite, et l’autre de droite à gauche. Cela permet de doubler la longueur de la phrase sans perdre trop d’informations.

Seq2seq avec attention

Le succès de l’approche ci-dessus a été de courte durée. Un autre document de Bahdanau, Cho, Bengio a suggéré qu’au lieu d’avoir un gigantesque réseau qui réduit le sens de la phrase entière en un seul vecteur, il serait plus logique qu’à chaque étape, nous concentrions l’attention uniquement sur les endroits pertinents dans la langue originale ayant un sens équivalent. C’est ce qu’on appelle le mécanisme d’attention.

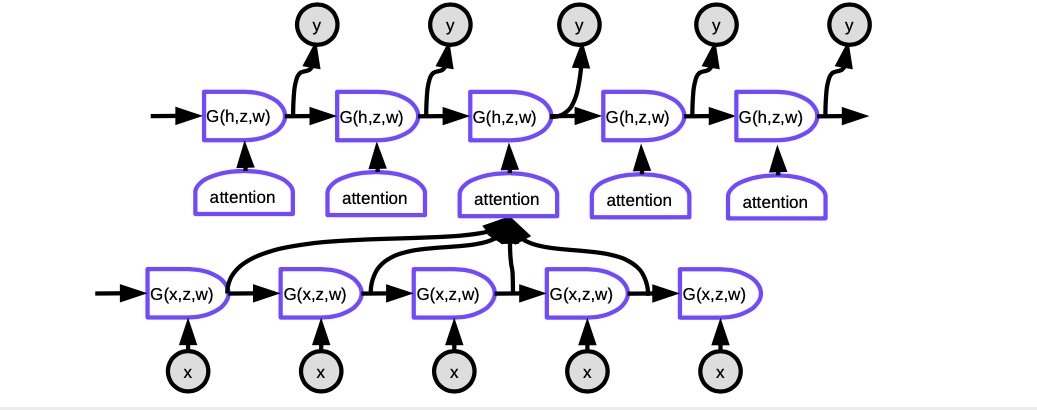
Figure 6 : Seq2Seq avec attention

Avec l’attention, pour produire le mot courant à chaque pas de temps, nous devons d’abord décider sur quelles représentations cachées des mots de la phrase d’entrée nous devons nous concentrer. Essentiellement, un réseau apprendra à évaluer dans quelle mesure chaque entrée codée correspond à la sortie actuelle du décodeur. Ces scores sont normalisés par une fonction softmax, puis les coefficients sont utilisés pour calculer une somme pondérée des états cachés dans l’encodeur à différents pas de temps. En ajustant les pondérations, le système peut ajuster la zone des entrées sur laquelle se concentrer. La magie de ce mécanisme est que le réseau utilisé pour calculer les coefficients peut être entraîné par rétropropagation. Il n’est pas nécessaire de les construire à la main !

Les mécanismes d’attention ont complètement transformé la traduction automatique des neurones. Plus tard en 2017, une équipe de Google a proposé le transformer, où chaque couche et groupe de neurones met en œuvre l’attention.

Réseaux mémoire

Les réseaux mémoire sont issus du travail de Facebook, lancé par Antoine Bordes en 2014 et Sainbayar Sukhbaatar en 2015. L’idée d’un réseau mémoire est qu’il y a deux parties importantes dans le cerveau. La première est le cortex, qui est l’endroit où est la mémoire à long terme. L’autre est l’hippocampe qui envoie des « fils » presque partout dans le cortex. On pense que l’hippocampe est utilisé pour la mémoire à court terme, se souvenant de choses pendant une période relativement courte. La théorie dominante est que lorsque l’on dort, il y a beaucoup d’informations transférées de l’hippocampe au cortex pour être consolidées dans la mémoire à long terme puisque l’hippocampe a une capacité limitée. Pour un réseau mémoire, il y a une entrée au réseau, $x$, qui est comparé à des vecteurs $k_1, k_2, k_3, \cdots$ (« clés ») via un produit scalaire. En les faisant passer par une fonction softmax, on obtient un tableau de nombres dont la somme est égale à un. Il y a un ensemble d’autres vecteurs $v_1, v_2, v_3, \cdots$ (« valeurs »). On multiplie ces vecteurs par les scalaires provenant de la softmax et l’addition de ces vecteurs donne le résultat (mécanisme ressemblant fortement à l’attention).

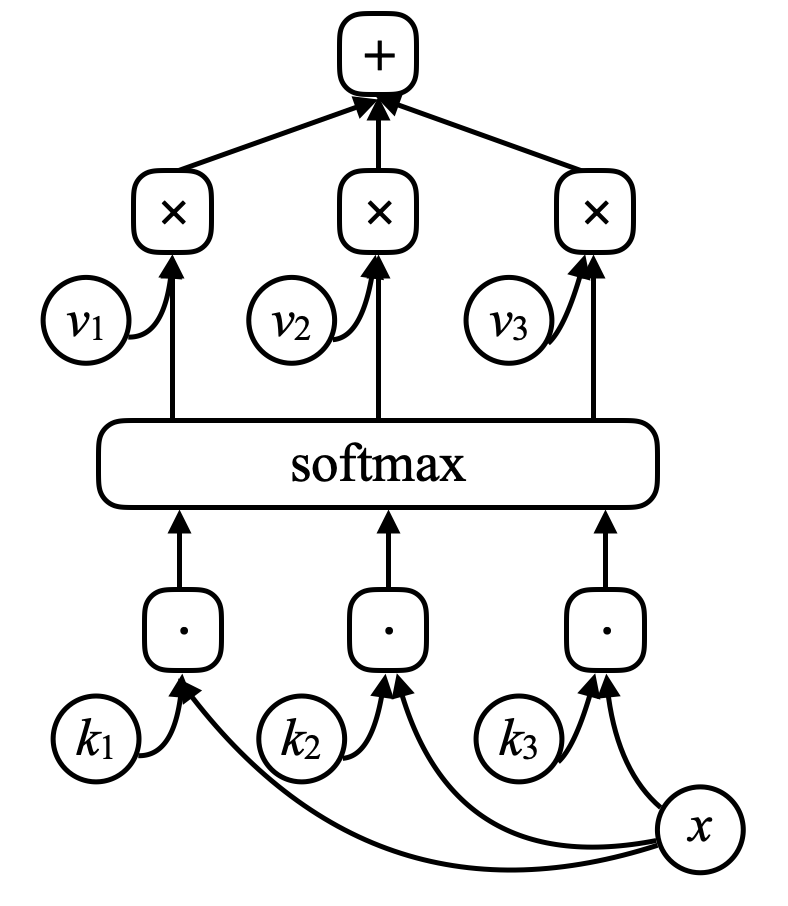
Figure 7 : Réseau mémoire

Si l’une des clés (par exemple $k_i$) correspond exactement à $x$, alors le coefficient associé à cette clé sera très proche de $1$. La sortie du système sera donc grossièrement $v_i$. Il s’agit de la mémoire associative adressable. La mémoire associative est que si l’entrée correspond à une clé, nous obtenons cette valeur. Et ce n’est qu’une version différentiable douce, ce qui permet de faire une rétropropagation et de changer les vecteurs par descente de gradient.

Les auteurs ont donné une histoire au système en lui donnant une séquence de phrases. Les phrases sont encodées en vecteurs en les faisant passer à travers un réseau neuronal qui n’a pas été pré-entraîné. Les phrases sont renvoyées à la mémoire. Lorsqu’on pose une question au système, elle est encodée puis est passée dans le réseau mémoire qui produit un $x$ et la mémoire renvoie une valeur. Cette valeur (ainsi que l’état précédent du réseau) est utilisée pour accéder à nouveau à la mémoire. Après un apprentissage intensif, ce modèle apprend en fait à stocker des histoires et à répondre à des questions.

Dans un réseau mémoire, il y a un réseau neuronal qui prend une entrée et produit ensuite une adresse pour la mémoire, renvoie la valeur au réseau, continue et produit finalement une sortie. Cela ressemble beaucoup à un ordinateur puisqu’il y a une unité centrale et une mémoire externe pour lire et écrire.

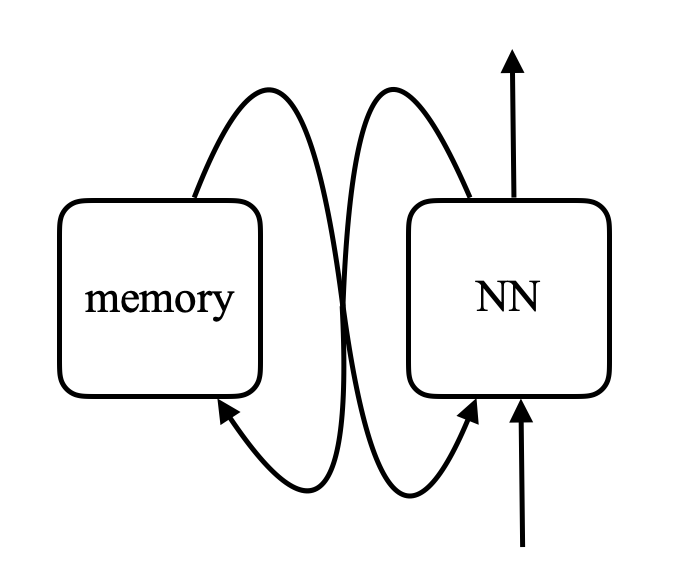
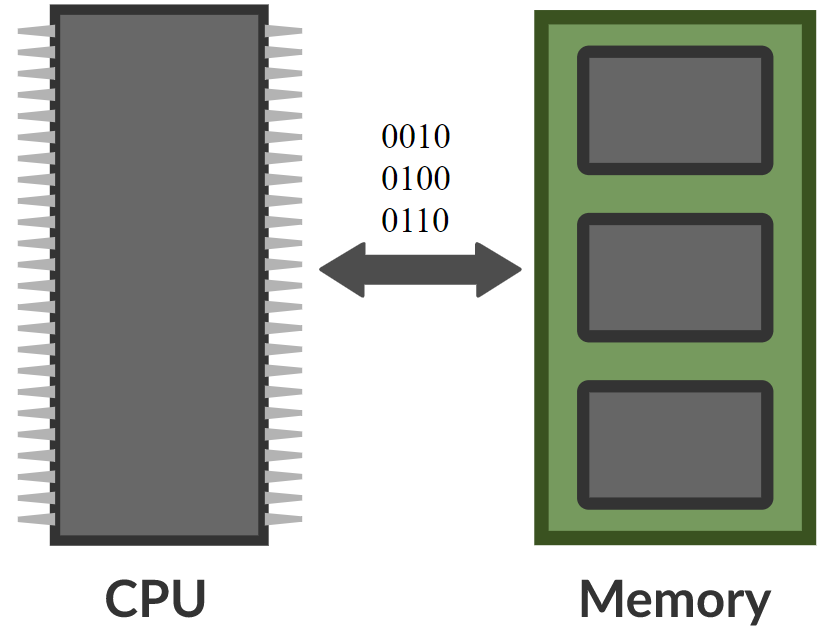
Figure 8 : Comparaison entre le réseau mémoire et l'ordinateur

Des gens pensent qu’on peut en fait construire des ordinateurs différentiables à partir de cela. Un exemple est la Neural Turing Machine de DeepMind, qui a été rendue publique sur arXiv trois jours après la publication de l’article de Facebook.

L’idée est de comparer des entrées à des clés, de générer des coefficients et de produire des valeurs. C’est ce que fait basiquement un transformer. Un transformer est essentiellement un réseau de neurones dans lequel chaque groupe de neurones est l’un de ces réseaux.