Applications des ConvNets

Reconnaissance des codes postaux

Dans les cours des semaines précédentes, nous avons démontré qu’un réseau convolutif peut reconnaître des chiffres. Cependant, la question demeure de savoir comment le modèle choisit chaque chiffre et évite les perturbations avec les chiffres voisins. L’étape suivante consiste à détecter les objets qui ne se chevauchent pas et à utiliser l’approche générale de la suppression non maximale (NMS en anglais pour Non-Maximum Suppression). Etant donné l’hypothèse que l’entrée est une série de chiffres ne se chevauchants pas, la stratégie consiste à entraîner plusieurs réseaux convolutifs et à utiliser soit un vote majoritaire, soit à choisir les chiffres correspondant au score le plus élevé généré par le réseau convolutif.

Reconnaissance avec les ConvNets

Nous présentons ici la tâche consistant à reconnaître un code postal constitué de 5 chiffres ne se chevauchant pas. Le système n’a reçu aucune instruction sur la façon de séparer chaque chiffre, mais il sait qu’il doit prévoir 5 chiffres. Le système (figure 1) se compose de 4 ConvNets de taille différente, chacun produisant un ensemble de sorties. La sortie est représentée par des matrices. Les quatre matrices de sortie proviennent de modèles dont la dernière couche présente une largeur de noyau différente. Dans chaque sortie, il y a 10 lignes représentant les 10 chiffres de 0 à 9. Le plus grand carré blanc représente un score plus élevé dans cette catégorie. Dans ces quatre blocs de sortie, les tailles horizontales des dernières couches de noyaux sont respectivement de 5, 4, 3 et 2. La taille du noyau détermine la largeur de la fenêtre de visualisation du modèle en entrée, c’est pourquoi chaque modèle prédit des chiffres en fonction de différentes tailles de fenêtre. Le modèle effectue alors un vote majoritaire et sélectionne la catégorie qui correspond au score le plus élevé dans cette fenêtre. Pour extraire des informations utiles, il faut garder à l’esprit que toutes les combinaisons de caractères ne sont pas possibles. Ainsi une correction d’erreurs utilisant les restrictions d’entrée est utile afin de s’assurer que les sorties sont de véritables codes postaux.

Figure 1 : Multiples classifieurs pour la reconnaissance des codes postaux

Maintenant, il faut imposer l’ordre des caractères. L’astuce consiste à utiliser un algorithme de chemin le plus court. Comme on nous donne des plages de caractères possibles et le nombre total de chiffres à prévoir, nous pouvons aborder ce problème en calculant le coût minimum de production des chiffres et des transitions entre les chiffres. Le chemin doit être continu de la cellule inférieure gauche à la cellule supérieure droite du graphique. Il doit aussi contenir que des mouvements de gauche à droite et de bas en haut. De plus, si le même nombre est répété l’un à côté de l’autre, l’algorithme doit être capable de distinguer les nombres répétés au lieu de prédire un seul chiffre.

Détection des visages

Les ConvNets sont très performants dans les tâches de détection. La détection des visages ne fait pas exception. Pour effectuer la détection des visages, nous collectons un jeu de données d’images avec et sans visages sur lesquelles nous entraînons un ConvNet avec une taille de fenêtre de 30 $\times$ 30 pixels. Nous demandons alors au réseau de dire s’il y a un visage ou non. Une fois entraîné, nous appliquons le modèle à une nouvelle image et s’il y a des visages à peu près dans une fenêtre de 30 $\times$ 30 pixels, le ConvNet éclairera la sortie aux endroits correspondants. Cependant, deux problèmes se posent :

• les faux positifs : il y a de nombreuses façons pour qu’un morceau d’image ne soit pas un visage. Pendant la phase d’entraînement, le modèle peut ne pas toutes les voir (c’est-à-dire que notre jeu de données n’est pas pleinement représentatif). Par conséquent, le modèle peut souffrir d’un grand nombre de faux positifs au moment du test.

• la taille de visage différente : tous les visages ne sont pas de taille 30 $\times$ 30 pixels. Ainsi, les visages de tailles différentes peuvent ne pas être détectés. Une façon de traiter ce problème est de générer des versions multi-échelles de la même image. Le détecteur original détectera des visages d’environ 30 $\times$ 30 pixels. En appliquant une échelle sur l’image de facteur $\sqrt 2$, le modèle détectera les visages plus petits dans l’image originale puisque ce qui était de taille 30 $\times$ 30 est maintenant d’environ 20 $\times$ 20 pixels. Pour détecter des visages plus grands, nous pouvons réduire la taille de l’image. Ce procédé est peu coûteux car la moitié des dépenses provient du traitement de l’image originale non réduite. La somme des dépenses de tous les autres réseaux combinés est à peu près la même que le traitement de l’image originale non mise à l’échelle. La taille du réseau est le carré de la taille de l’image d’un côté, donc si vous réduisez l’image par $2$, le réseau que vous devez faire fonctionner est plus petit d’un facteur $2$. Le coût global est donc de $1+1/2+1/4+1/8+1/16+…$, ce qui donne 2. La réalisation d’un modèle multi-échelle ne fait donc que doubler le coût de calcul.

Un système de détection des visages à plusieurs échelles

Figure 2 : Système de détection des visages

Les cartes présentées (figure 3) indiquent les scores des détecteurs de visages. Ce détecteur de visage reconnaît les visages qui ont une taille de 20 $\times$ 20 pixels. En échelle fine (Scale 3 dans la figure 3), il y a beaucoup de scores élevés mais pas définitifs. Lorsque le facteur d’échelle augmente (Scale 6), nous voyons davantage de régions blanches groupées. Ces régions blanches représentent les visages détectés. Nous appliquons alors une suppression non maximale pour obtenir l’emplacement final du visage.

Figure 3 : Scores du détecteur de visage pour différents facteurs d'échelle

Suppression non maximale

Pour chaque région ayant un score élevé, il y a probablement un visage en dessous. Si plusieurs visages sont détectés très près du premier, cela signifie qu’un seul doit être considéré comme correct et que les autres sont faux. Dans le cas d’une suppression non maximale, nous prenons la zone la plus importante des cases de délimitation qui se chevauchent et nous supprimons les autres. Le résultat est alors une seule boîte englobante à l’emplacement optimal.

Negative mining

Nous avons vu comment un modèle peut se heurter à un grand nombre de faux positifs au moment de la phase de test car plusieurs objets peuvent ressembler à un visage de diverses façons. Aucun jeu d’entraînement ne peut contenir tous les objets qui ne sont pas des visages et ceux qui ressemblent à des visages. Nous pouvons atténuer ce problème grâce au negative mining (pêche à l’exemple négatif). Avec cette technique, nous exécutons notre modèle sur des entrées dont on sait qu’elles ne contiennent pas de visages. Tous les patchs sans visages mais que le modèle a détecté comme étant des visages sont alors ajoutés dans notre jeu de données d’exemples négatifs. Ensuite, nous recyclons le détecteur en utilisant le jeu de données négatives. Nous pouvons répéter ce processus pour augmenter la robustesse de notre modèle contre les faux positifs.

Segmentation sémantique

La segmentation sémantique est la tâche qui consiste à attribuer une catégorie à chaque pixel d’une image d’entrée.

ConvNets pour la vision adaptative à longue portée des robots

Dans ce projet, l’objectif était d’étiqueter des régions à partir d’images d’entrée afin qu’un robot puisse distinguer les routes des obstacles. Dans la figure, les régions vertes sont les zones sur lesquelles le robot peut rouler et les régions rouges sont les obstacles comme les herbes hautes. Pour entraîner le réseau à cette tâche, nous avons pris un patch de l’image et l’avons étiqueté manuellement comme étant traversable ou non (vert ou rouge). Nous entraînons ensuite le réseau convolutif sur les patchs en lui demandant de prédire la couleur du patch. Une fois que le système est suffisamment entraîné, il est appliqué à l’ensemble de l’image, en étiquetant toutes les régions de l’image en vert ou en rouge.

Figure 4 : ConvNets pour la vision adaptative à longue portée des robots (programme LAGR de la DARPA 2005-2008)

Il y avait cinq catégories pour la prédiction : 1) super vert, 2) vert, 3) violet, 4) obstacle rouge, 5) super rouge : un obstacle certain.

Étiquettes stéréo (Figure 4, colonne 2) :
Les images sont captées par les 4 caméras du robot, qui sont regroupées en 2 paires de vision stéréo. En utilisant les distances connues entre les caméras des paires stéréoscopiques, les positions de chaque pixel dans l’espace 3D sont ensuite estimées en mesurant les distances relatives entre les pixels qui apparaissent dans les deux caméras d’une paire stéréoscopique. C’est le même processus que notre cerveau utilise pour estimer la distance des objets que nous voyons. En utilisant les informations de position estimées, un plan est ajusté au sol et les pixels sont alors étiquetés en vert s’ils sont proches du sol et en rouge s’ils sont au-dessus.

Limitations et motivation pour les ConvNets :
La vision stéréo ne fonctionne que jusqu’à 10 mètres et la conduite d’un robot nécessite une vision à longue distance. Un ConvNet est cependant capable de détecter des objets à des distances beaucoup plus grandes, s’il est correctement entraîné.

Figure 5 : Pyramide invariante au changement d’échelle d’images avec des distances normalisées

Servie comme entrée modèle :
Un prétraitement important comprend la construction invariante au changement d’échelle d’images avec des distances normalisées (figure 5). Elle est similaire à ce que nous avons fait plus tôt dans ce cours lorsque nous avons essayé de détecter des visages de différentes tailles.

Sorties du modèle (figure 4, colonne 3) :
Le modèle produit une étiquette pour chaque pixel de l’image jusqu’à l’horizon. Ce sont les sorties du classifieur d’un ConvNet multi-échelles.

Comment le modèle devient adaptatif :
Les robots ont un accès continu aux étiquettes stéréo, ce qui permet au réseau de se réentraîner et de s’adapter au nouvel environnement dans lequel il se trouve. A noter que seule la dernière couche du réseau est entraînée à nouveau. Les couches précédentes sont entraînées en laboratoire et fixées.

Performances du système :
En essayant d’obtenir une coordonnée GPS de l’autre côté d’une barrière, le robot a perçu cette barrière et a planifié un itinéraire qui l’a évitée. Ceci grâce à la détection d’objets situés à une distance de 50 à 100 m.

Limitation : Dans les années 2000, les ressources de calcul étaient limitées. Le robot était capable de traiter environ une image par seconde, ce qui signifie qu’il ne pouvait pas détecter une personne qui se trouvait sur son chemin pendant une seconde entière avant de pouvoir réagir. La solution à cette limitation est un modèle d’odométrie visuelle à faible coût. Il n’est pas basé sur les réseaux de neurones, a une vision d’environ 2,5m mais réagit rapidement.

Analyse et étiquetage des scènes

Dans cette tâche, le modèle produit une catégorie d’objets (bâtiments, voitures, ciel, etc.) pour chaque pixel. L’architecture est également multi-échelle (figure 6).

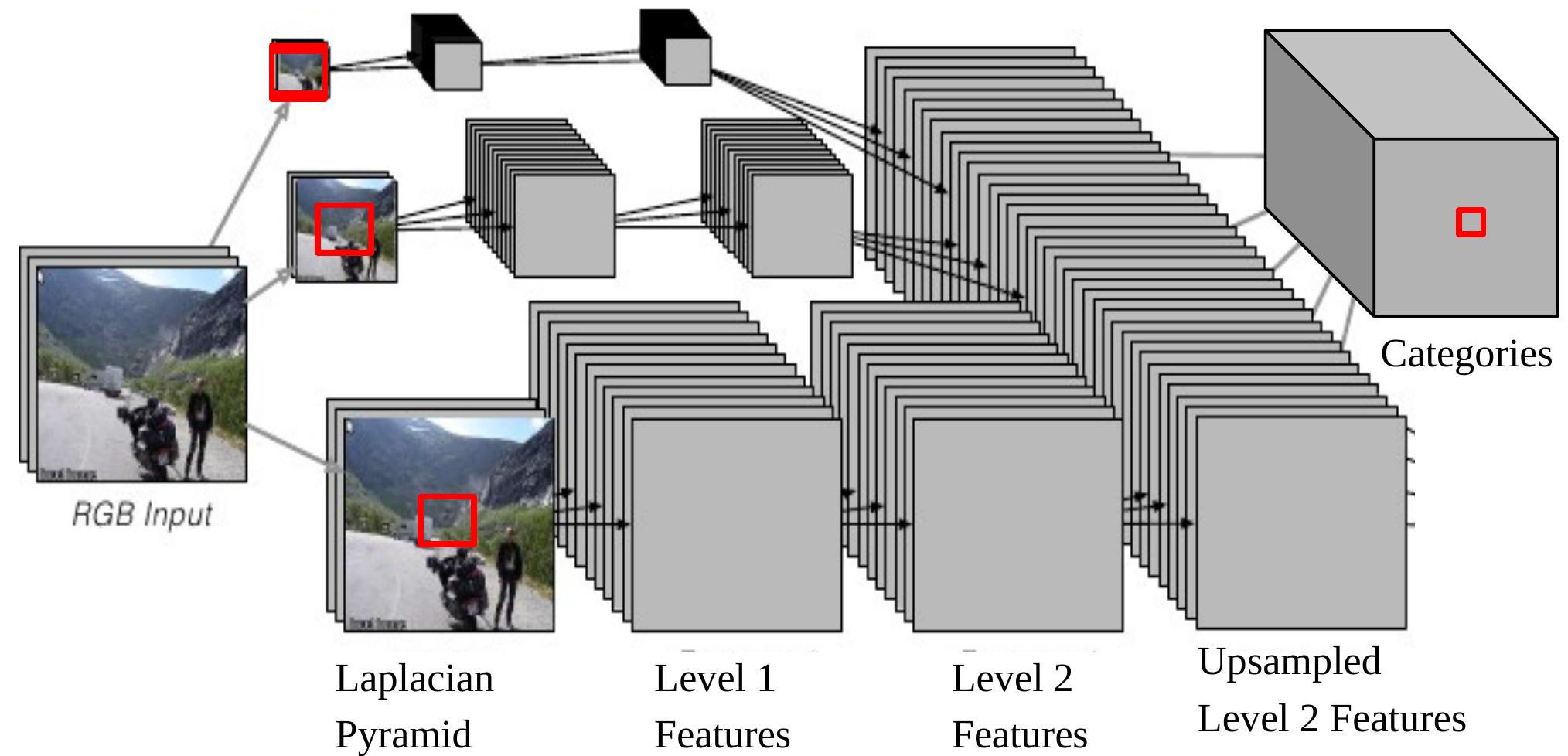
Figure 6 : ConvNet multi-échelles pour l'analyse des scènes

Si nous rétropropageons une sortie du ConvNet sur l’entrée, cela correspond à une fenêtre d’entrée de taille $46 \times 46$ sur l’image originale au bas de la pyramide de Laplace. Cela signifie que nous utilisons le contexte des pixels $46 \times 46$ pour décider de la catégorie du pixel central. Cependant, parfois, la taille de ce contexte n’est pas suffisante pour déterminer la catégorie des objets plus grands. L’approche multi-échelles permet une vision plus large en fournissant des images supplémentaires redimensionnées comme entrées :

1. Prendre la même image, la réduire séparément d’un facteur 2 et d’un facteur 4.
2. Ces deux images supplémentaires redimensionnées sont envoyées au même ConvNet (mêmes poids, mêmes noyaux) et nous obtenons deux autres ensembles de caractéristiques de niveau 2.
3. Échantillonner ces caractéristiques de façon à ce qu’elles aient la même taille que les caractéristiques de niveau 2 de l’image originale.
4. Empiler les trois ensembles de caractéristiques (suréchantillonnées) et envoyer-les à un classifieur.

Maintenant, la plus grande taille effective du contenu, qui provient de l’image redimensionnée à 1/4, est de $184\times 184 (46\times 4=184)$.

Performance : sans post-traitement et en fonctionnant image par image, le modèle fonctionne très rapidement, même sur du matériel standard. Il a une taille assez réduite de données d’entraînement (2 000 à 3 000), mais les résultats sont toujours très performants.