Comprendre les convolutions et autograd

Comprendre la convolution 1D

Au lieu d’utiliser la matrice $A$ de la semaine précédente, nous allons changer la largeur de la matrice pour la taille du noyau $k$. Par conséquent, chaque ligne de la matrice est un noyau. Nous pouvons utiliser les noyaux en les empilant et en les déplaçant (voir la figure 1). Nous pouvons alors avoir $m$ couches de hauteur $n-k+1$.

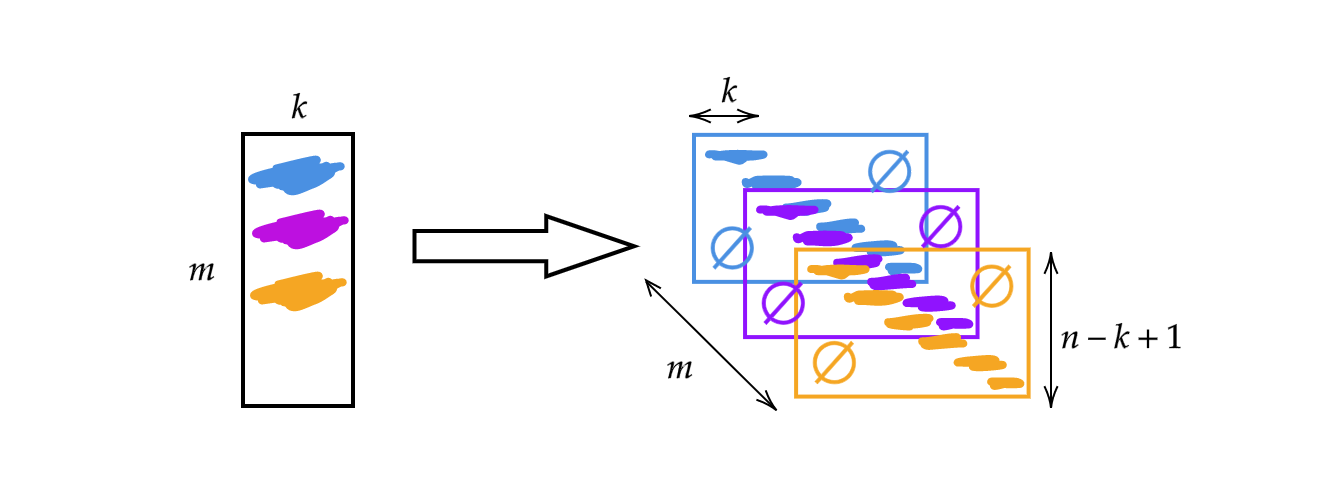
Figure 1 : Illustration de la convolution 1D

La sortie est $m$ vecteurs de taille $n-k+1$.

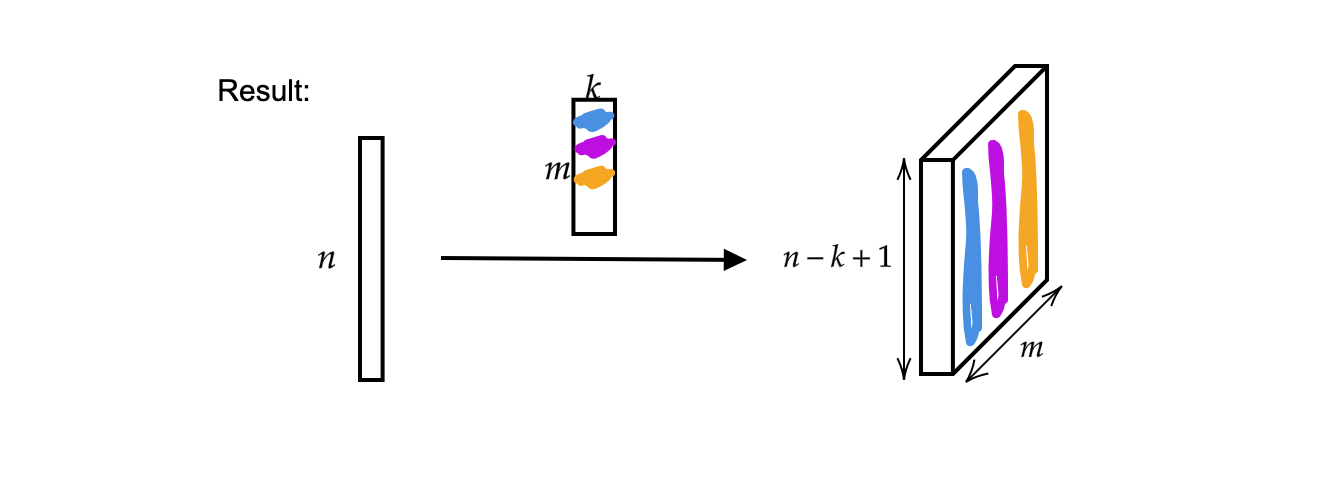
Figure 2 : Résultat de la convolution 1D

De plus, un seul vecteur d’entrée peut être considéré comme un signal monophonique.

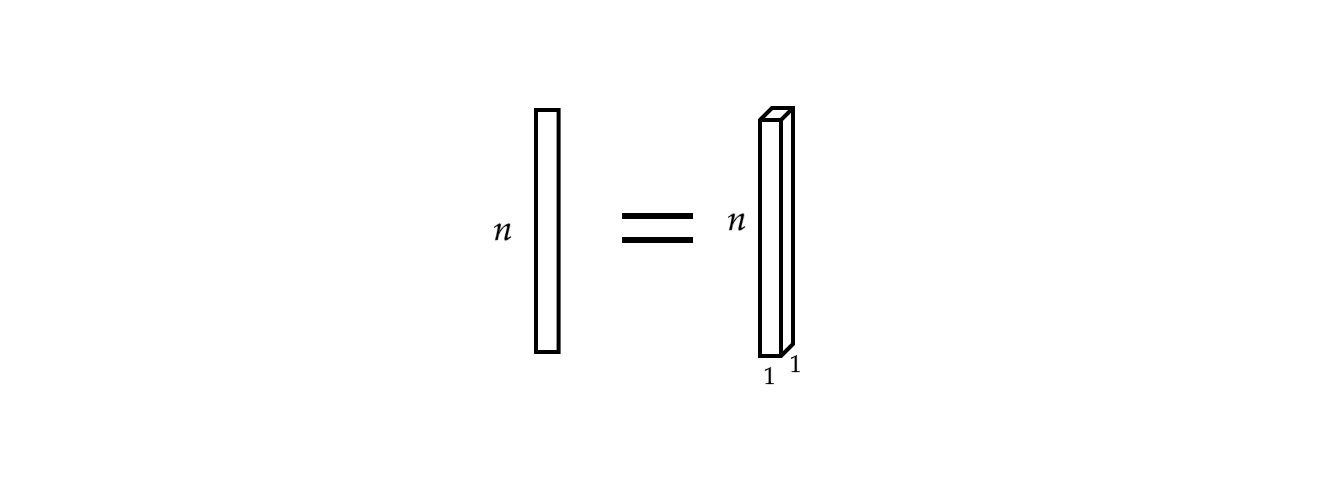
Figure 3 : Signal monophonique

Maintenant, l’entrée $ x:\Omega\rightarrow\mathbb{R}^{c}$ avec $\Omega = \lbrace 1, 2, 3, \cdots \rbrace \subset \mathbb{N}^1$ (puisque c’est un signal de dimension $1$ / il a un domaine de dimension $1$) et dans ce cas le numéro de canal $c$ est $1$. Lorsque $c = 2$, cela devient un signal stéréophonique.

Pour la convolution 1D, nous pouvons simplement calculer le produit scalaire, noyau par noyau (voir figure 4).

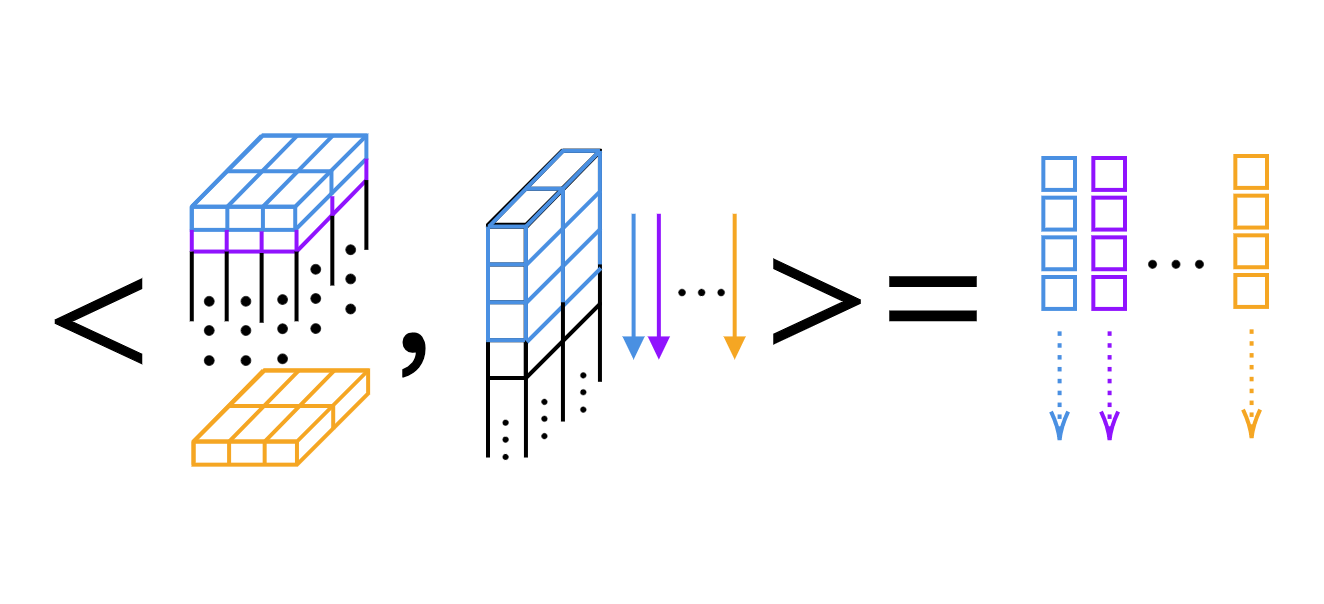
Figure 4 : Produit scalaire couche par couche de la convolution 1D

Dimension des noyaux et largeur des sorties dans PyTorch

Astuce : on peut utiliser le question mark dans IPython pour avoir accès aux documents de fonctions. Par exemple,

Init signature :
nn.Conv1d(
	in_channels, # nombre de canaux dans l'image d'entrée
	out_channels, # nombre de canaux produits par la convolution
	kernel_size, # taille du noyau en convolution
	stride=1, # pas de la convolution
	padding=0, # rembourage de 0 ajouté aux deux côtés de l'entrée
	dilatation=1, # espacement entre les éléments du noyau
	groups=1, # nombre de connexions bloquées de l'entrée à la sortie
	bias=True, # si `True`, ajoute un biais appris à la sortie
	padding_mode='zeros', # valeurs acceptées `zeros` et `circular`.
)

Convolution 1D

Nous avons une convolution de dimension $1$ allant de $2$ canaux (signal stéréophonique) à $16$ canaux ($16$ noyaux) avec une taille de noyau de $3$ et un pas de $1$. Nous avons ensuite $16$ noyaux avec une épaisseur de $2$ et une longueur de $3$. Supposons que le signal d’entrée ait un batch de taille $1$ (un signal), de $2$ canaux et $64$ échantillons. La couche de sortie résultante a $1$ signal, des $16$ canaux et la longueur du signal est de $62$ ($=64-3+1$). De plus, si nous affichons la taille du biais, nous constaterons qu’elle de $16$, puisque nous avons un biais par poids.

conv = nn.Conv1d(2, 16, 3) # 2 canaux (signal stéréo), 16 noyaux de taille 3
conv.weight.size() # sortie : torch.Size([16, 2, 3])
conv.bias.size() # sortie : torch.Size([16])

x = torche.rand(1, 2, 64) # batch de taille 1, 2 canaux, 64 échantillons
conv(x).size() # sortie : torch.Size([1, 16, 62])

conv = nn.Conv1d(2, 16, 5) # 2 canaux, 16 noyaux de taille 5
conv(x).size() # sortie : torch.Size([1, 16, 60])

Convolution 2D

Nous définissons d’abord les données d’entrée comme un $1$ échantillon, $20$ canaux (disons que nous utilisons une image hyperspectrale) avec une hauteur de $64$ et une largeur de $128$. La convolution 2D a $20$ canaux en entrée et $16$ noyaux de taille de $3\times5$. Après la convolution, la donnée en sortie a un $1$ échantillon, $16$ canaux avec une hauteur de $62$ ($=64-3+1$) et une largeur de $124$ ($=128-5+1$).

x = torch.rand(1, 20, 64, 128) # 1 échantillon, 20 canaux, hauteur 64, et largeur 128
conv = nn.Conv2d(20, 16, (3, 5))  # 20 canaux, 16 noyaux, la taille des noyaux est de 3 x 5
conv.weight.size() # sortie : torch.Size([16, 20, 3, 5])
conv(x).size() # sortie : torch.Size([1, 16, 62, 124])

Si nous voulons atteindre la même dimensionnalité, nous pouvons rembourrer. En continuant le code ci-dessus, nous pouvons ajouter de nouveaux paramètres à la fonction de convolution : stride=1 et padding=(1, 2), ce qui signifie $1$ dans la direction $y$ ($1$ en haut et $1$ en bas) et $2$ dans la direction $x$. Le signal de sortie est alors de la même taille que le signal d’entrée. Le nombre de dimensions nécessaires pour stocker la collection de noyaux lorsque vous effectuez une convolution 2D est de $4$.

# 20 canaux, 16 noyaux de taille 3 x 5, pas de 1, rembourrage 1 et 2
conv = nn.Conv2d(20, 16, (3, 5), 1, (1, 2))
conv(x).size() # sortie : torch.Size([1, 16, 64, 128])

Comment fonctionne le gradient automatique ?

Dans cette section, nous allons demander à Pytorch de vérifier tous les calculs sur les tenseurs afin que nous puissions effectuer le calcul des dérivés partielles.

• Créer un tenseur $2\times2$ $\boldsymbol{x}$ avec des capacités d’accumulation de gradients
• Enlever $2$ à tous les éléments de $\boldsymbol{x}$ et obtenir $\boldsymbol{y}$
  Si nous affichons y.grad_fn, nous obtenons l’objet <SubBackward0 à 0x12904b290>, ce qui signifie que y est généré par le module de soustraction $\boldsymbol{x}-2$. On peut aussi utiliser y.grad_fn.next_functions[0][0].variable pour dériver le tenseur original.
• Faire d’autres opérations : $\boldsymbol{z} = 3\boldsymbol{y}^2$
• Calculer la moyenne de $\boldsymbol{z}$

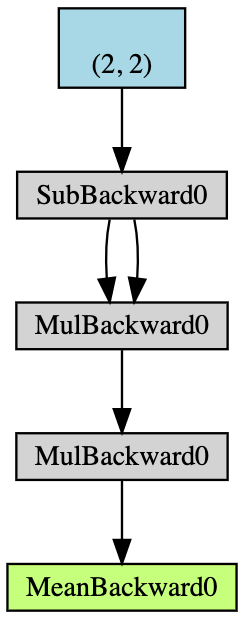
Figure 5 : Exemple d’organigramme d'auto-gradient

La rétropropagation est utilisée pour calculer les gradients. Dans cet exemple, le processus de rétropropagation peut être considéré comme le calcul du gradient $\frac{d\boldsymbol{a}}{d\boldsymbol{x}}$. Après avoir calculé manuellement $\frac{d\boldsymbol{a}}{d\boldsymbol{x}}$ comme validation, nous pouvons constater que l’exécution de a.backward() nous donne la même valeur que x.grad.

Voici le processus de calcul de la rétropropagation à la main :

Chaque fois que nous utilisons une dérivée partielle dans PyTorch, nous obtenons la même forme que les données originales. Mais la bonne jacobienne devrait être la transposée.

Vers plus de folie

Maintenant que nous avons un vecteur $1\times3$ $x$, assignons $2x$ à $y$ et doublons $y$ jusqu’à ce que sa norme soit inférieure à $1000$. En raison du caractère aléatoire que nous avons pour $x$, nous ne pouvons pas connaître directement le nombre d’itérations lorsque la procédure se termine.

x = torch.randn(3, requires_grad=True)

y = x * 2
i = 0
while y.data.norm() < 1000:
    y = y * 2
    i += 1

Cependant, nous pouvons facilement le déduire en connaissant les gradients dont nous disposons.

gradients = torch.FloatTensor([0.1, 1.0, 0.0001])
y.backward(gradients)

print(x.grad)
tensor([1.0240e+02, 1.0240e+03, 1.0240e-01])
print(i)
9

Quant à l’inférence, nous pouvons utiliser requires_grad=True pour indiquer que nous voulons suivre l’accumulation du gradient comme indiqué ci-dessous. Si nous omettons requires_grad=True dans la déclaration de $x$ ou $w$ et appelons backward() sur $z$, il y aura une erreur d’exécution due au fait que nous n’avons pas d’accumulation de gradient sur $x$ ou $w$.

# x et w qui permettent l'accumulation de gradients
x = torch.arange(1., n + 1, requires_grad=True)
w = torch.ones(n, requires_grad=True)
z = w @ x
z.backward()
print(x.grad, w.grad, sep='\n')

Nous pouvons avoir with torch.no_grad() pour omettre l’accumulation de gradient.

x = torch.arange(1., n + 1)
w = torch.ones(n, requires_grad=True)

# Tous les tenseurs n'auront pas l'accumulation de gradient
with torch.no_grad():
    z = w @ x

try:
    z.backward()# PyTorch va retourner une erreur ici, puisque z n'a pas de grad accum.
except RuntimeError as e:
    print('RuntimeError!!! >:[')
    print(e)

Plus de choses : des gradients personnalisés

Au lieu d’opérations numériques de base, nous pouvons générer nos propres modules / fonctions qui peuvent être branchés sur le graphe neural. Le notebook Jupyter se trouve ici.
Pour ce faire, nous devons partir de la fonction torch.autograd.Function et remplacer les fonctions forward() et backward(). Par exemple, si nous voulons entraîner des réseaux, nous devons obtenir la propagation en avant dans le réseau et connaître les dérivées partielles de l’entrée par rapport à la sortie, de sorte que nous puissions utiliser ce module en tout point du code. Ensuite, en utilisant la rétropropagation (règle de la chaîne), nous pouvons insérer la chose n’importe où dans la chaîne d’opérations, à condition de connaître les dérivées partielles de l’entrée par rapport à la sortie.

Dans ce cas, il y a trois exemples de modules personnalisés dans le notebook, les modules add, split, et max. Par exemple, le module d’ajout personnalisé :

# Module personnalisé supplémentaire
class MyAdd(torch.autograd.Function):

    @staticmethod
    def forward(ctx, x1, x2):
        # ctx est un contexte où nous pouvons sauvegarder les calculs pour la rétropropagation
        ctx.save_for_backward(x1, x2)
        return x1 + x2

    @staticmethod
    def backward(ctx, grad_output):
        x1, x2 = ctx.saved_tensors
        grad_x1 = grad_output * torch.ones_like(x1)
        grad_x2 = grad_output * torch.ones_like(x2)
        # on a besoin de retourner les gradients pour la phase avant
        return grad_x1, grad_x2

Si nous avons l’addition de deux choses et que nous obtenons un résultat, nous devons écraser la fonction forward comme ceci. Et lorsque nous rétropropagation, les gradients sont copiés sur les deux côtés. Nous écrasons donc la fonction backward en copiant.

Pour les fonctions split et max, consultez le code pour la façon dont nous écrasons les fonctions forward et backward dans le notebook. Pour argmax, cela sélectionne l’indice de la chose la plus élevée. Ainsi l’indice de la plus élevée devrait être de $1$ et $0$ pour les autres.