Propriétés des signaux naturels

Propriétés des signaux naturels

Tous les signaux peuvent être considérés comme des vecteurs. Par exemple, un signal audio est un signal 1D $\boldsymbol{x} = [x_1, x_2, \cdots, x_T]$ où chaque valeur $x_t$ représente l’amplitude de la forme d’onde au moment $t$. Pour comprendre ce que dit une personne, votre cochlée convertit d’abord les vibrations de la pression atmosphérique en signaux, puis votre cerveau utilise un modèle linguistique pour convertir ce signal en une langue, c’est-à-dire qu’il doit choisir l’énoncé le plus probable compte tenu du signal. Pour la musique, le signal est stéréophonique et possède 2 canaux ou plus pour vous donner l’illusion que le son provient de plusieurs directions. Même s’il a 2 canaux, c’est toujours un signal 1D car le temps est la seule variable le long de laquelle le signal change.

Une image est un signal 2D parce que l’information est représentée dans l’espace. Notez que chaque point peut être un vecteur en soi. Cela signifie que si nous avons des canaux $d$ dans une image, chaque point spatial dans l’image est un vecteur de dimension $d$. Une image couleur a des plans RVB, ce qui signifie $d = 3$. Pour tout point $x_{i,j}$, cela correspond à l’intensité des couleurs rouge, verte et bleue respectivement.

Nous pouvons même représenter le langage avec la logique ci-dessus. Chaque mot correspond à un vecteur one-hot avec un à la position où il se trouve dans notre vocabulaire et des zéros partout ailleurs. Cela signifie que chaque mot est un vecteur de la taille du vocabulaire.

Les signaux de données naturels suivent ces propriétés :

1. Stationnarité : certains motifs se répètent tout au long d’un signal. Dans les signaux audio, nous observons le même type de motifs encore et encore dans le domaine temporel. Dans les images, cela signifie que nous pouvons nous attendre à ce que des motifs visuels similaires se répètent dans toute la dimensionnalité.
2. Localité : les points proches sont plus corrélés que les points éloignés. Pour un signal 1D, cela signifie que si nous observons un pic à un certain point $t_i$, nous nous attendons à ce que les points dans une petite fenêtre autour de $t_i$ aient des valeurs similaires à $t_i$ mais pour un point $t_j$ éloigné de $t_i$, $x_{t_i}$ a très peu d’influence sur $x_{t_j}$. Plus formellement, la convolution entre un signal et son homologue inversé a un pic lorsque le signal chevauche parfaitement sa version inversée. Une convolution entre deux signaux 1D (corrélation croisée) n’est rien d’autre que leur produit scalaire, qui est une mesure de la similarité ou de la proximité des deux vecteurs. Ainsi, l’information est contenue dans des portions et des parties spécifiques du signal. Pour les images, cela signifie que la corrélation entre deux points dans une image diminue à mesure que l’on s’éloigne des points. Si le pixel $x_{0,0}$ est bleu, la probabilité que le pixel suivant ($x_{1,0},x_{0,1}$) soit également bleu est assez élevée, mais lorsque l’on se déplace vers l’extrémité opposée de l’image ($x_{-1,-1}$), la valeur de ce pixel est indépendante de la valeur du pixel à $x_{0,0}$.
3. Compositionnalité : tout dans la nature est composé de parties qui sont composées de sous-parties et ainsi de suite. Par exemple, les caractères forment des chaînes de caractères qui forment des mots, qui forment ensuite des phrases. Les phrases peuvent être combinées pour former des documents. La compositionnalité permet d’expliquer le monde.

Si nos données sont stationnaires, locales et composées, nous pouvons les exploiter grâce à des réseaux qui utilisent l’ éparsité, le partage des poids et l’empilement des couches.

Exploitation des propriétés des signaux naturels pour construire l’invariance et l’équivariance

Localité $\Rightarrow$ éparsité

La figure 1 montre un réseau à 5 couches entièrement connecté. Chaque flèche représente un poids à multiplier par les entrées. Comme on peut le voir, ce réseau est très coûteux en termes de calcul.

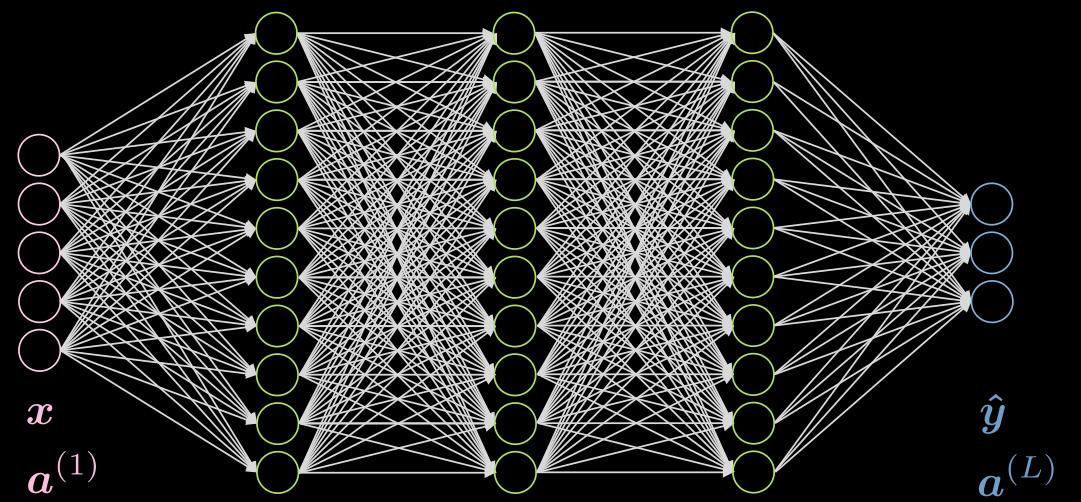
Figure 1 : Réseau entièrement connecté

Si nos données montrent une localité, chaque neurone doit être connecté à seulement quelques neurones locaux de la couche précédente. Ainsi, certaines connexions peuvent être supprimées comme le montre la figure 2. La figure 2(a) représente un réseau entièrement connecté. En profitant de la propriété de localisation de nos données, nous supprimons les connexions entre les neurones éloignés dans la figure 2(b). Bien que les neurones de la couche cachée (vert) de la figure 2(b) ne couvrent pas la totalité de l’entrée, l’architecture globale pourra prendre en compte tous les neurones d’entrée. Le champ réceptif (abrégé RF pour receptive field en anglais) est le nombre de neurones des couches précédentes, que chaque neurone d’une couche particulière peut voir ou a pris en compte. Par conséquent, le RF de la couche de sortie est de 3 pour la couche cachée, le RF de la couche cachée est de 3 pour la couche d’entrée, mais le RF de la couche de sortie est de 5 pour la couche d’entrée.

Figure 2(a) : Avant l’application de l’éparsité	Figure 2(b) : Après l’application de l’éparsité

Stationnarité $\Rightarrow$ partage des paramètres

Si nos données sont stationnaires, nous pourrions utiliser un petit ensemble de paramètres plusieurs fois dans l’architecture du réseau. Par exemple, dans notre réseau épars, figure 3(a), nous pouvons utiliser un ensemble de 3 paramètres partagés (jaune, orange et rouge). Le nombre de paramètres passera alors de 9 à 3 ! La nouvelle architecture pourrait même fonctionner mieux car nous disposons de plus de données pour l’entraînement de ces poids spécifiques. Les poids après avoir appliqué l’éparsité et le partage des paramètres sont appelés noyau de convolution.

Figure 3(a) : Avant l’application du partage des paramètres	Figure 3(b) : Après l’application du partage des paramètres

Voici quelques avantages de l’utilisation du partage des paramètres et de l’éparsité :

• Partage des paramètres :
  • une convergence plus rapide
  • une meilleure généralisation
  • ne concerne pas la taille de l’entrée
  • Indépendance du noyau $\Rightarrow$ forte parallélisation
• L’éparsité de connexion :
  • montant de calcul nécessaire réduit

La figure 4 montre un exemple de noyaux sur des données 1D, où la taille du noyau est : 2 (nombre de noyaux) $\times$ 7 (épaisseur de la couche précédente) $\times$ 3 (nombre de connexions/poids uniques).

Le choix de la taille du noyau est empirique. Une convolution 3 $\times$ 3 semble être la taille minimale pour les données spatiales. La convolution de taille 1 peut être utilisée pour obtenir une couche finale qui peut être appliquée à une image d’entrée plus grande. Une taille de noyau de nombre pair peut réduire la qualité des données, c’est pourquoi nous avons toujours une taille de noyau de nombre impair, généralement 3 ou 5.

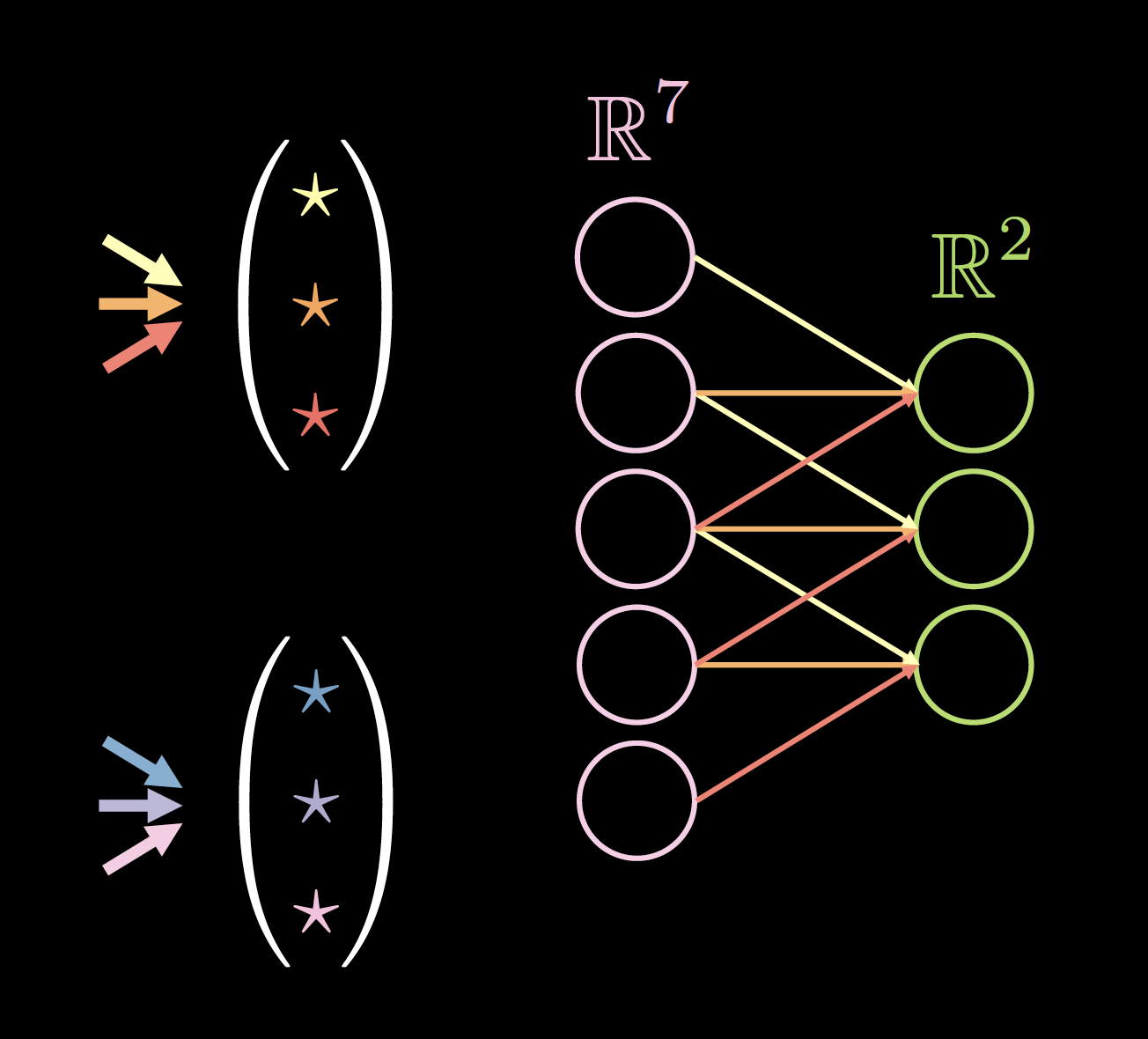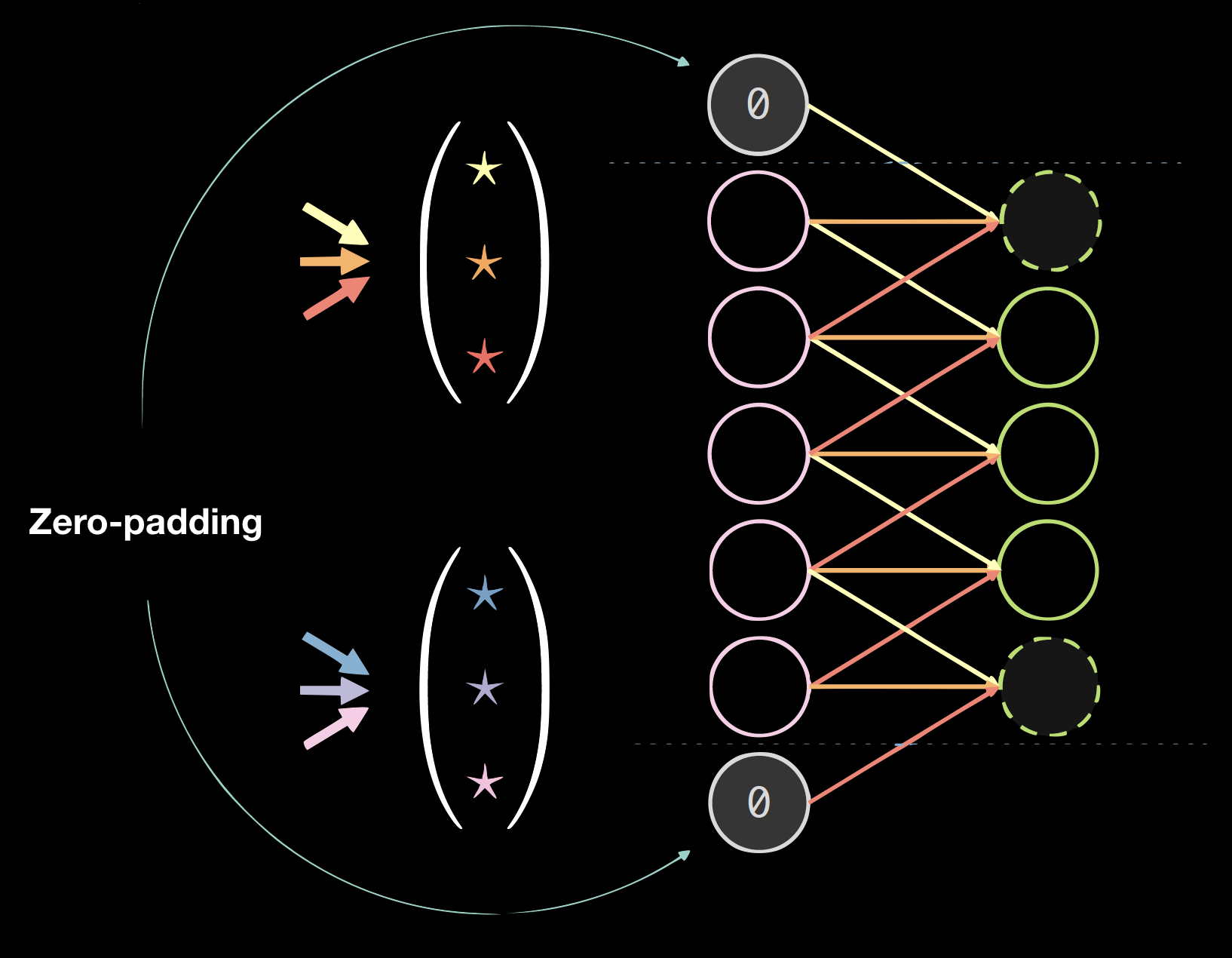Figure 4(a) : Noyaux sur données 1D	Figure 4(b) : Données avec un rembourrage de 0

Rembourrage (padding)

Le rembourrage nuit généralement aux résultats finaux, mais il est pratique du point de vue programmatique. Nous utilisons généralement le zero-padding : size = (taille du noyau - 1)/2.

ConvNet spatial standard

Un ConvNet spatial standard a les propriétés suivantes :

• Couches multiples
  • Convolution
  • Non-linéarité (ReLU et Leaky)
  • Pooling
  • Normalisation par batch
• Connexion résiduelle

La normalisation par batch et les connexions résiduelles sont très utiles pour que le réseau s’entraîne bien. Des parties d’un signal peuvent être perdues si trop de couches ont été empilées, de sorte que des connexions résiduelles garantissent un chemin de bas en haut et aussi un chemin pour les gradients venant de haut en bas.

Dans la figure 5, alors que l’image d’entrée contient principalement des informations spatiales en deux dimensions (à part les informations caractéristiques, qui sont la couleur de chaque pixel), la couche de sortie est épaisse. À mi-chemin, il y a un compromis entre les informations spatiales et les informations caractéristiques, et la représentation devient plus dense. Par conséquent, à mesure que nous montons dans la hiérarchie, nous obtenons une représentation plus dense car nous perdons les informations spatiales.

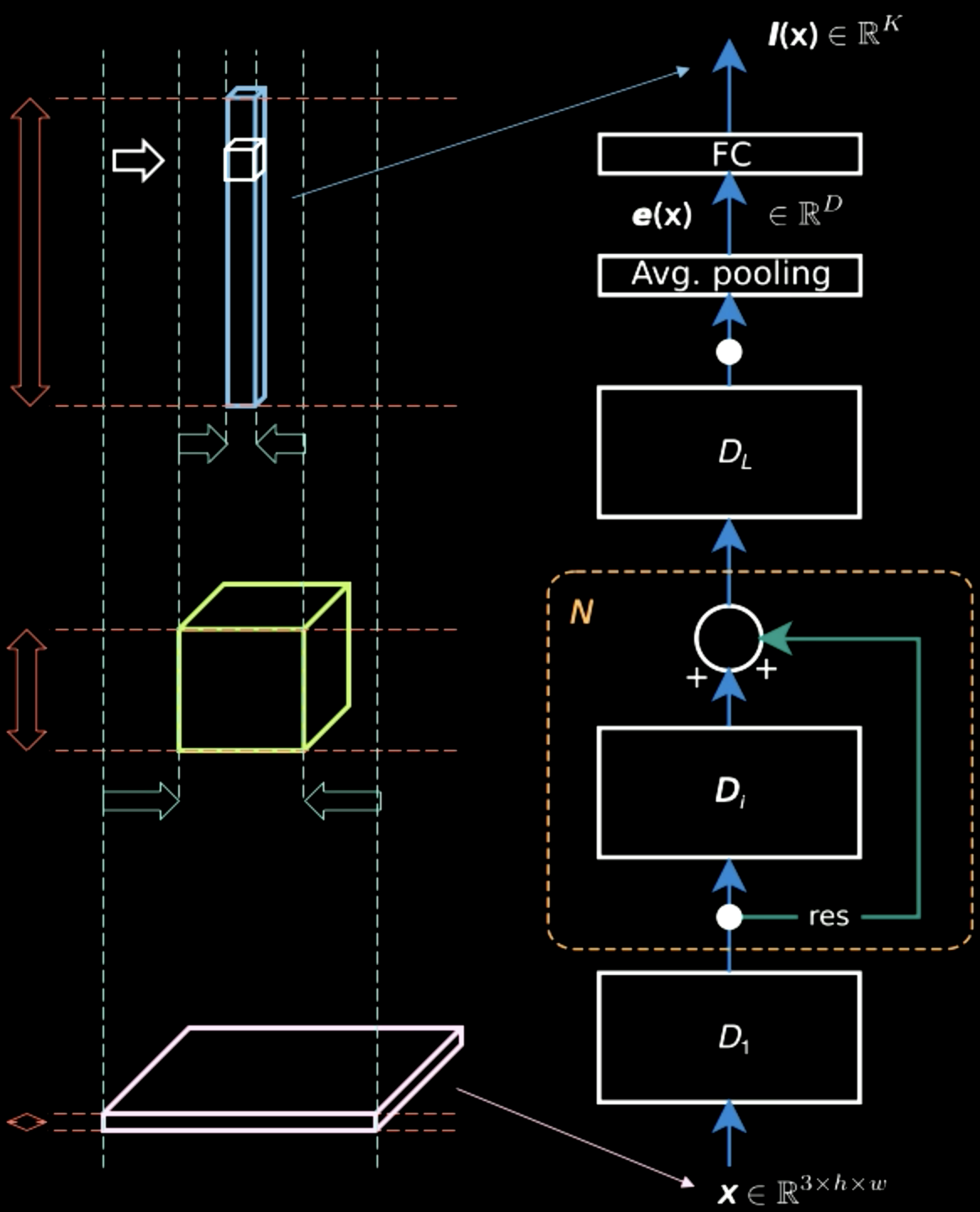
Figure 5 : Représentations de l'information remontant la hiérarchie

Pooling

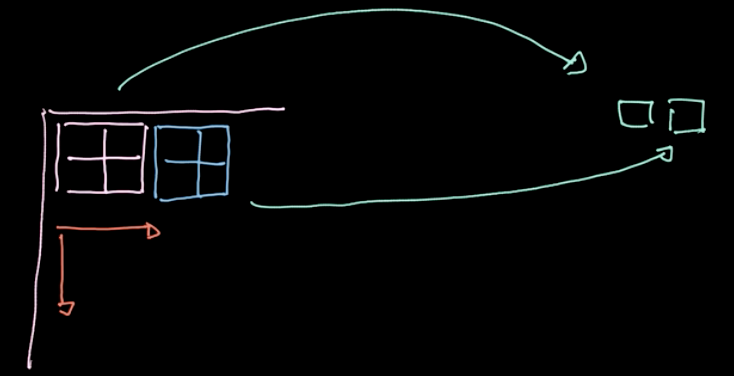
Figure 6 : Illustration du pooling

Un opérateur spécifique, $L_p$-norm, est appliqué aux différentes régions (voir figure 6). Un tel opérateur ne donne qu’une seule valeur par région (1 valeur pour 4 pixels dans notre exemple). Nous itérons ensuite sur l’ensemble des données région par région, en prenant des mesures basées sur le pas. Si nous commençons avec $m \times n$ données avec $c$ canaux, nous finirons avec $\frac{m}{2} \times \frac{n}{2}$ données toujours avec des canaux $c$ (voir figure 7). Le pooling n’est pas paramétré néanmoins, nous pouvons choisir différents types comme le max-pooling, l’average-pooling, etc. Le but principal du pooling est de réduire la quantité de données afin que nous puissions faire les calculs dans un délai raisonnable.

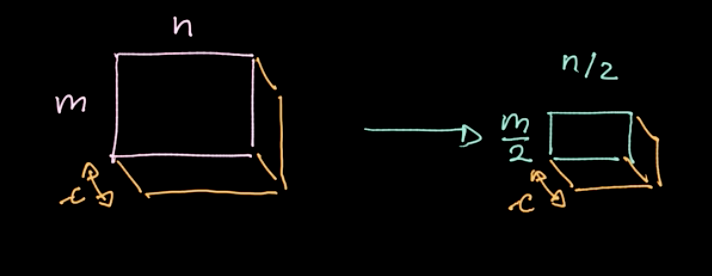
Figure 7 : Résultats du pooling

ConvNet - Notebook Jupyter

La version anglaise du notebook Jupyter se trouve ici. La version en français est disponible ici. Pour faire fonctionner le notebook, assurez-vous d’avoir installé l’environnement pDL comme indiqué dans le fichier README.md.

Dans ce notebook Jupyter, nous entraînons un perceptron multicouche (réseau entièrement connecté) et un ConvNet pour la tâche de classification sur le jeu de données MNIST. Notez que les deux réseaux ont un nombre égal de paramètres (figure 8).

Figure 8 : Instances provenant du jeu de données MNIST

Avant l’entraînement, nous normalisons nos données afin que l’initialisation du réseau corresponde à notre distribution de données (très important !). De plus, on s’assure que les cinq opérations / étapes suivantes sont présentes dans notre entraînement :

1. Alimentation du modèle en données
2. Calcul de la perte
3. Nettoyage le cache des gradients accumulés avec zero_grad()
4. Calcul des gradients
5. Exécution d’une étape dans l’optimiseur

Tout d’abord, nous entraînons les deux réseaux aux données normalisées du MNIST. La précision du réseau entièrement connecté s’est avérée être de 87 %, tandis que celle du réseau ConvNet s’est révélée être de 95 %. Avec le même nombre de paramètres, le ConvNet a réussi à entraîner beaucoup plus de filtres. Dans le réseau entièrement connecté, les filtres qui essaient d’obtenir des dépendances entre des choses qui sont plus éloignées et des choses qui sont proches, sont entraînés et sont complètement gaspillés. Au lieu de cela, dans le ConvNet, tous ces paramètres se concentrent sur la relation entre les pixels voisins.

Ensuite, nous effectuons une permutation aléatoire de tous les pixels dans toutes les images de notre jeu de données MNIST. Cela transforme notre figure 8 en figure 9. Nous entraînons ensuite les deux réseaux sur ce jeu de données modifié.

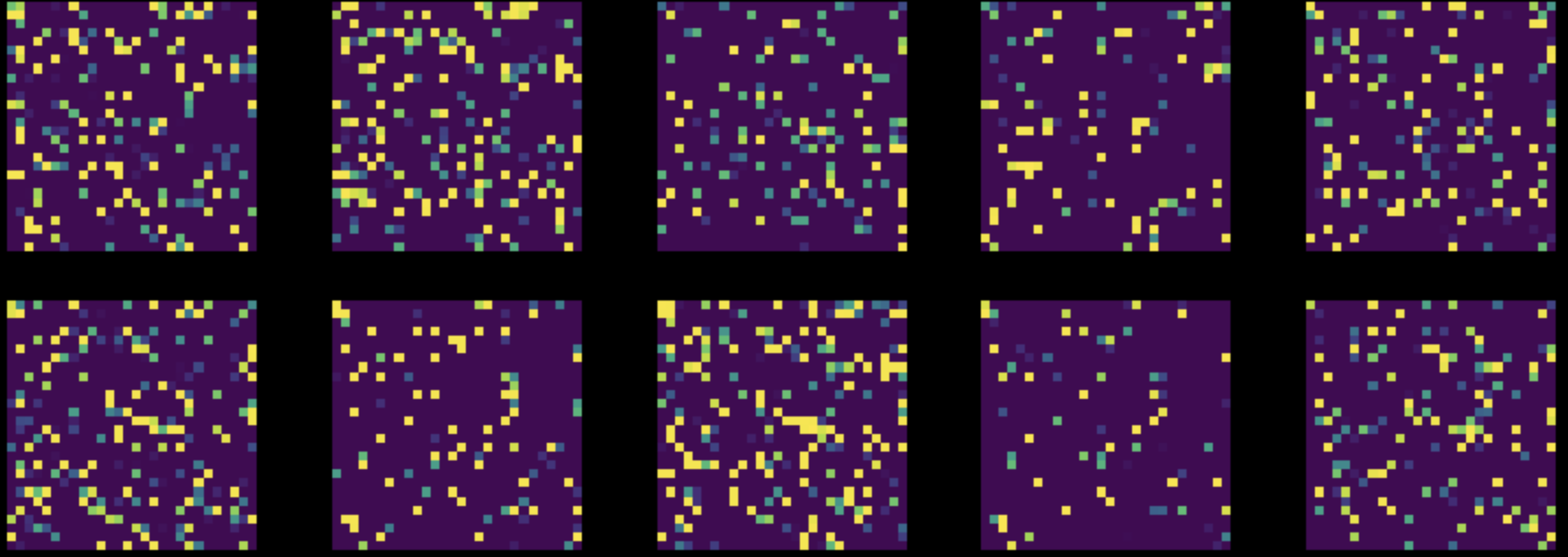
Figure 9 : Instances provenant du jeu de données MNIST permuté

Les performances du réseau entièrement connecté sont restées pratiquement inchangées à 85 %, mais la précision du ConvNet est tombée à 83 %. En effet, après une permutation aléatoire, les images ne possèdent plus les trois propriétés de localité, de stationnarité et de composition, exploitables par un ConvNet.