Evolutions des ConvNets, Architectures, Details et Avantages de l’implementation

Proto-ConvNets et evolution vers les ConvNets modernes

Proto-ConvNets sur de petits jeux de données

Inspiré par les travaux de Fukushima sur la modélisation du cortex visuel, l’utilisation de la hiérarchie cellulaire simple/complexe combinée à l’entraînement supervisé et à la rétropropagation a conduit à la création du premier ConvNet à l’université de Toronto en 1988-89 par Yann. Les expériences reposaient sur un petit jeux de données de 320 chiffres écrits à la souris d’ordinateur. Les performances des architectures suivantes ont été comparées :

1. Une seule couche entièrement connectée (FC pour Fully connected en anglais)
2. Deux couches FC
3. Couches connectées localement sans partage de poids
4. Réseau contraint avec poids partagés et connexions locales
5. Réseau contraint avec poids partagés et connexions locales 2 : c’est-à-dire davantage de cartes de caractéristiques (feature maps en anglais)

Les réseaux les plus performants (réseau contraint avec poids partagés) ont la plus forte généralisabilité et constituent la base des ConvNets modernes. La couche FC unique a quant à elle tendance à faire du surentraînement (overfitting).

Les premiers « vrais» réseaux convolutifs au Bell Labs

Après avoir intégrés Bell Labs, Yann a orienté ses recherches vers l’utilisation de codes postaux manuscrits de la poste américaine pour entraîner un ConvNet plus important :

• 256 (16$\times$16) couche d’entrée
• 12 5$\times$5 noyaux avec un pas de 2 (pas de 2 pixels) : la couche suivante a une résolution plus faible
• PAS de pooling séparé

ConvNets avec pooling

L’année suivante, certains changements ont été apportés : un pooling séparé a été introduit. Le pooling séparé est réalisé en faisant la moyenne des valeurs en entrée, en ajoutant un biais et en passant à une fonction non linéaire (fonction tangente hyperbolique). Le pooling de taille 2$\times$2 a été effectuée avec un pas de 2, réduisant ainsi les résolutions de moitié.

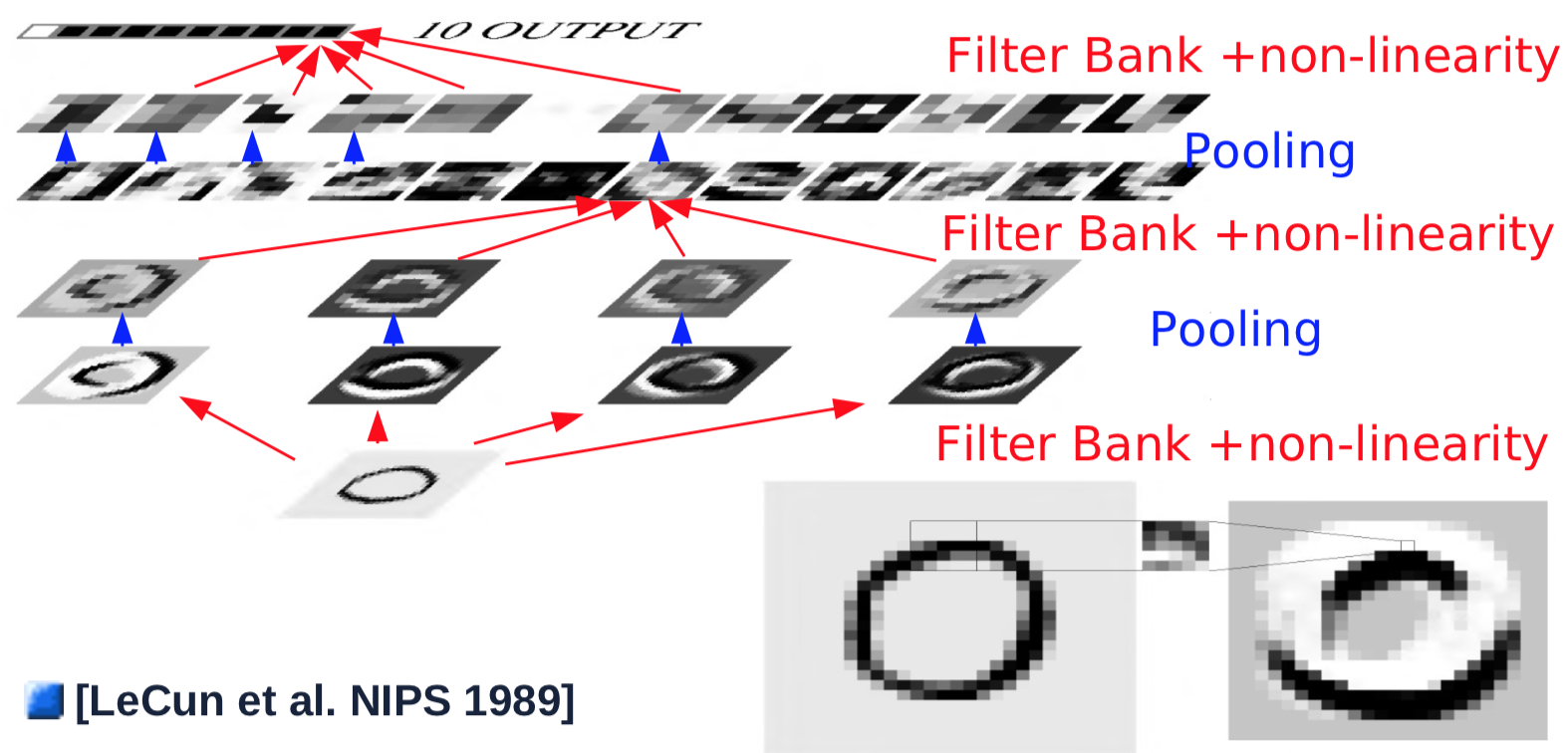
Figure 1 : Architecture ConvNet

Voici un exemple de couche convolutionnelle unique :

1. On prend une entrée de taille 32$\times$32
2. La couche de convolution passe un noyau de taille 5$\times$5 avec un pas de 1 sur l’image, ce qui donne une carte de caractéristiques de taille 28$\times$28.
3. On passe la carte de caractéristiques à travers une fonction non linéaire : taille 28$\times$28
4. On passe à la couche de pooling qui fait une moyenne sur une fenêtre de 2$\times$2 avec un pas de 2 : taille 14$\times$14
5. On répète des étapes 1 à 4 pour 4 noyaux

Les combinaisons simples convolution/pooling de la première couche détectent généralement des caractéristiques simples, telles que des bords orientés. Après la première couche de convolution/pooling, l’objectif est de détecter des combinaisons d’éléments des couches précédentes. Pour ce faire, les étapes 2 à 4 sont répétées avec plusieurs noyaux sur les cartes de caractéristiques des couches précédentes et sont additionnées dans une nouvelle carte de caractéristiques :

1. Un nouveau noyau de 5$\times$5 est glissé sur toutes les cartes de caractéristiques des couches précédentes, et les résultats sont additionnés. Note : dans l’expérience de Yann en 1989, la connexion n’est pas complète pour les calculs. Les paramètres modernes imposent généralement des connexions complètes : taille 10$\times$10
2. On passe la sortie de la convolution à une fonction non linéaire : taille 10$\times$10
3. On répète les étapes 1 et 2 pour 16 noyaux
4. On passe le résultat à la couche de pooling qui moyenne sur une fenêtre de taille 2$\times$2 avec un pas de 2 : taille 5$\times$5 de chaque cartes de caractéristiques

Pour générer une sortie, on effectue la dernière couche de convolution, qui semble être une connexion complète mais qui est en fait convolutive.

1. La dernière couche de convolution fait glisser un noyau de 5$\times$5 sur toutes les cartes de caractéristiques, avec des résultats résumés : taille 1$\times$1
2. On passe par une fonction non linéaire : taille 1$\times$1
3. On génère la sortie unique pour une catégorie
4. On répète toutes les étapes précédentes pour chacune des 10 catégories (en parallèle)

Voir cette animation sur le site d’Andrej Karpathy sur la façon dont les convolutions modifient la forme des cartes de caractéristiques de la couche suivante. L’article complet est disponible ici.

Équivariance des changements

Figure 2 : Équivariance des changements

Comme le montre l’animation, la translation de l’image d’entrée entraîne la même translation des cartes de caractéristiques. Cependant, les changements dans les cartes de caractéristiques sont mis à l’échelle par des opérations de convolution/pooling. Par exemple, le pooling 2$\times$2 de pas 2 réduira le décalage de 1 pixel de la couche d’entrée à 0,5 pixel dans les cartes de caractéristiques suivantes. La résolution spatiale est alors échangée contre un plus grand nombre de types d’éléments, ce qui rend la représentation plus abstraite et moins sensible aux décalages et aux distorsions.

Décomposition de l’architecture globale

L’architecture générique des ConvNets peut être décomposée en plusieurs archétypes de couches de base :

• Normalisation
  • Ajustement du blanchiment (facultatif)
  • Méthodes soustractives, par exemple : suppression moyenne, filtre passe-haut
  • Divise : normalisation des contrastes locaux, normalisation de la variance
• Banques de filtres
  • Augmenter la dimensionnalité
  • Projection sur une base surcomplète
  • Détections d’arêtes
• Non-linéarités
  • éparsification
  • Rectified Linear Unit (ReLU) : $\text{ReLU}(x) = \max(x, 0)$.
• Pooling
  • Agrégation sur une carte de caractéristique

  • Max-pooling : $\text{MAX}= \text{Max}_i(X_i)$

  • Lp-Norm-pooling: \(\text{L}p= \left(\sum_{i=1}^n \|X_i\|^p \right)^{\frac{1}{p}}\)

  • Log-Prob-pooling: $\text{Prob}= \frac{1}{b} \left(\sum_{i=1}^n e^{b X_i} \right)$

LeNet5 et reconnaissance des chiffres

Implémentation de LeNet5 dans PyTorch

LeNet5 se compose des couches suivantes (1 étant la couche la plus élevée) :

1. Log-softmax
2. Couche entièrement connectée de dimensions 500$\times$10
3. ReLu
4. Couche entièrement connectée de dimensions (4$\times$4$\times$50)$\times$500
5. Max-pooling de dimensions 2$\times$2, pas de 2.
6. ReLu
7. Convolution avec 20 canaux de sortie, noyau 5$\times$5, pas de 1.
8. Max-pooling de dimensions 2$\times$2, pas de 2.
9. ReLu
10. Convolution avec 20 canaux de sortie, noyau 5$\times$5, pas de 1.

L’entrée est une image en échelle de gris de 32$\times$32 (1 canal d’entrée).

LeNet5 peut être implémenté dans PyTorch avec le code suivant :

class LeNet5(nn.Module):
    def __init__(self):
        super().__init__()
        self.conv1 = nn.Conv2d(1, 20, 5, 1)
        self.conv2 = nn.Conv2d(20, 20, 5, 1)
        self.fc1 = nn.Linear(4*4*50, 500)
        self.fc2 = nn.Linear(500, 10)

    def forward(self, x):
        x = F.relu(self.conv1(x))
        x = F.max_pool2d(x, 2, 2)
        x = F.relu(self.conv2(x))
        x = F.max_pool2d(x, 2, 2)
        x = x.view(-1, 4*4*50)
        x = F.relu(self.fc1)
        x = self.fc2(x)
    return F.logsoftmax(x, dim=1)

Bien que fc1 et fc2 soient des couches entièrement connectées, elles peuvent être considérées comme des couches convolutionnelles dont les noyaux couvrent l’ensemble de l’entrée. Les couches entièrement connectées sont utilisées à des fins d’efficacité.

Le même code peut être exprimé en utilisant n.séquentiel mais il est dépassé.

Avantages des ConvNets

Dans un réseau entièrement convolutif, il n’est pas nécessaire de préciser la taille de l’entrée. Cependant, la modification de la taille de l’entrée modifie la taille de la sortie.

Prenons l’exemple d’un système de reconnaissance de l’écriture cursive. Il n’est pas nécessaire de diviser l’image d’entrée en segments. Nous pouvons appliquer le ConvNet sur toute l’image : les noyaux couvriront tous les emplacements de l’image entière et enregistreront la même sortie, quel que soit l’emplacement du motif. Appliquer le ConvNet sur une image entière est beaucoup moins coûteux que de l’appliquer à plusieurs endroits séparément. Aucune segmentation préalable n’est nécessaire, ce qui est un soulagement car la tâche de segmenter une image est similaire à la reconnaissance d’une image.

Exemple : MNIST

LeNet5 est entraîné sur les images du jeu de données MNIST de taille 32$\times$32 pour classer les chiffres individuels au center de l’image. L’augmentation des données a été appliquée en déplaçant le chiffre autour, en changeant la taille du chiffre, en insérant des chiffres sur le côté. Il a également été entraîné avec une 11ème catégorie qui ne représentait rien de ce qui précède. Les images étiquetées par cette catégorie ont été générées soit en produisant des images vierges, soit en plaçant des chiffres sur le côté mais pas au center.

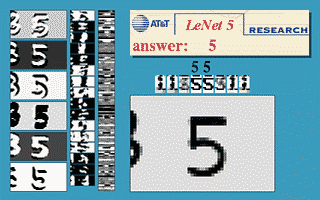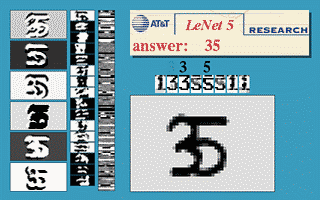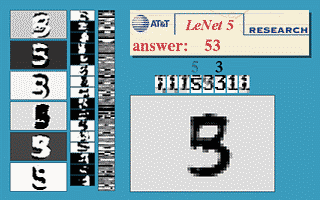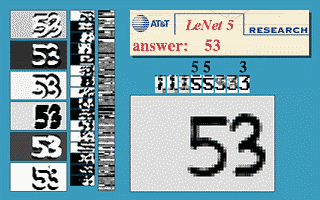
Figure 3 : ConvNet à fenêtre coulissante

L’image ci-dessus montre qu’un réseau LeNet5 entraîné sur $32\times32$ peut être appliqué sur une image d’entrée $32\times64$ pour reconnaître le chiffre à plusieurs endroits.

Problème de liaison des caractéristiques

Quel est le problème de la liaison des caractéristiques ?

Les spécialistes des neurones visuels et de la vision par ordinateur ont le problème de définir l’objet comme un objet. Un objet est une collection de caractéristiques, mais comment lier toutes les caractéristiques pour former cet objet ?

Comment le résoudre ?

Nous pouvons résoudre ce problème de liaison de caractéristiques en utilisant un ConvNet très simple : seulement deux couches de convolutions avec des poolings plus deux autres couches entièrement connectées sans mécanisme spécifique pour cela, étant donné que nous avons suffisamment de non-linéarités et de données pour entraîner notre ConvNet.

Figure 4 : Liaison des caractéristiques

L’animation ci-dessus montre la capacité du ConvNet à reconnaître différents chiffres en déplaçant un seul trait, ce qui démontre sa capacité à résoudre les problèmes de liaison des caractéristiques, c’est-à-dire à reconnaître les caractéristiques de manière hiérarchique et compositionnelle.

Exemple : longueur d’entrée dynamique

Nous pouvons construire un ConvNet avec 2 couches de convolution avec un pas de 1 et deux couches de pooling avec un pas de 2 de telle sorte que le pas global soit de 4. Ainsi, si nous voulons obtenir une nouvelle sortie, nous devons décaler notre fenêtre d’entrée de 4. Pour être plus explicite, nous pouvons voir la figure ci-dessous (unités vertes). Tout d’abord, nous avons une entrée de taille 10, et nous effectuons une convolution de taille 3 pour obtenir 8 unités. Ensuite, nous effectuons un pooling de taille 2 pour obtenir 4 unités. De même, nous répétons la convolution et le pooling et nous obtenons finalement une sortie de taille 1.

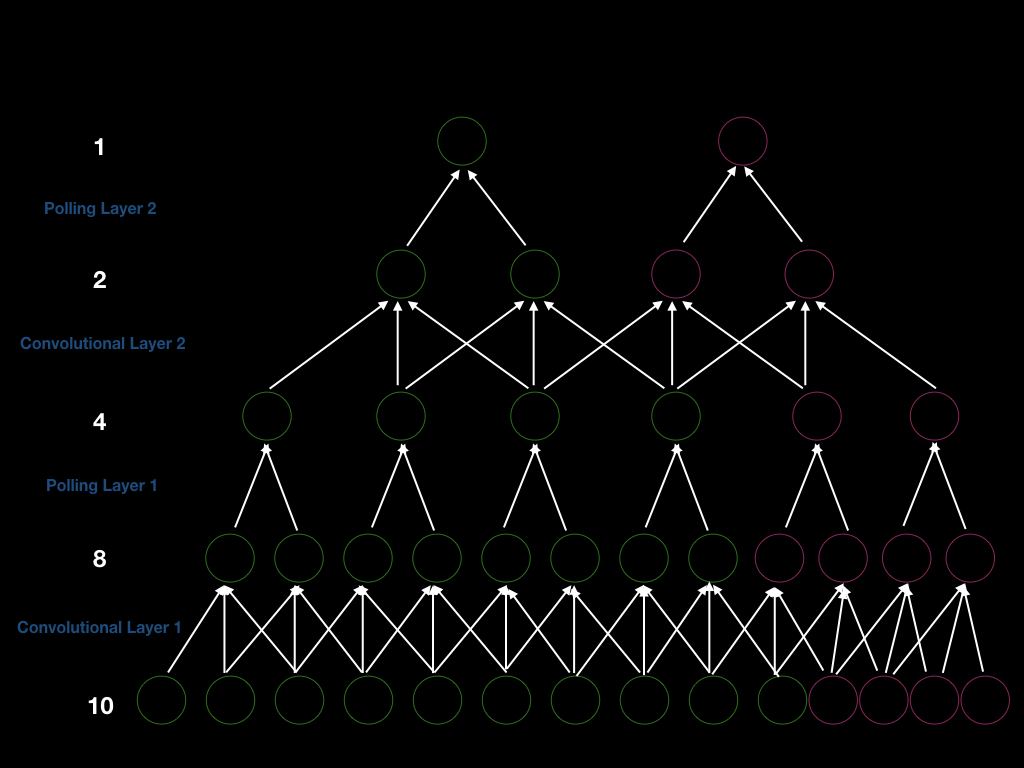
Figure 5 : Architecture ConvNet sur la liaison de la taille d'entrée des variantes

Supposons que nous ajoutions 4 unités à la couche d’entrée (unités roses au-dessus), de sorte que nous puissions obtenir 4 unités supplémentaires après la première couche de convolution, 2 unités supplémentaires après la première couche de pooling, 2 unités supplémentaires après la deuxième couche de convolution et 1 unité supplémentaire en sortie. Par conséquent, la taille de la fenêtre pour générer une nouvelle sortie est de 4 (deux fois 2 pas) . De plus, cela démontre que si nous augmentons la taille de l’entrée, nous augmenterons la taille de chaque couche, ce qui prouve la capacité des ConvNets à gérer les entrées de longueur dynamique.

Pour quelles taches les ConvNets sont performants ?

Les ConvNets sont performants pour les signaux naturels qui se présentent sous la forme de réseaux multidimensionnels et ont trois propriétés principales :

1. La localisation : la première est qu’il existe une forte corrélation locale entre les valeurs. Si nous prenons deux pixels proches d’une image naturelle, il est très probable que ces pixels aient la même couleur. Plus deux pixels sont éloignés l’un de l’autre, plus la similitude entre eux diminue. Les corrélations locales peuvent nous aider à détecter des caractéristiques locales, ce que font les ConvNets. Si nous alimentons le ConvNet avec des pixels permutés, il ne sera pas performant dans la reconnaissance des images d’entrée, tandis que le FC ne sera pas affecté. La corrélation locale justifie les connexions locales.
2. La stationnarité : le deuxième caractère est que les caractéristiques sont essentielles et peuvent apparaître n’importe où sur l’image, justifiant les partages des poids et le pooling. De plus, les signaux statistiques sont uniformément distribués, ce qui signifie que nous devons répéter la détection des caractéristiques pour chaque emplacement sur l’image d’entrée.
3. La compostionnalité : le troisième caractère est que les images naturelles sont compositionnelles, ce qui signifie que les caractéristiques composent une image de manière hiératique. Cela justifie l’utilisation de plusieurs couches de neurones, ce qui correspond aussi étroitement aux recherches de Hubel et Weisel sur les cellules simples et complexes.

En outre, les ConvNets sont utilisés sur les vidéos, les images, les textes et la reconnaissance vocale.