Visualisation de la transformation des paramètres des réseaux neuronaux et concepts fondamentaux de la convolution

Visualisation des réseaux de neurones

Dans cette section, nous allons visualiser le fonctionnement interne d’un réseau de neurones.

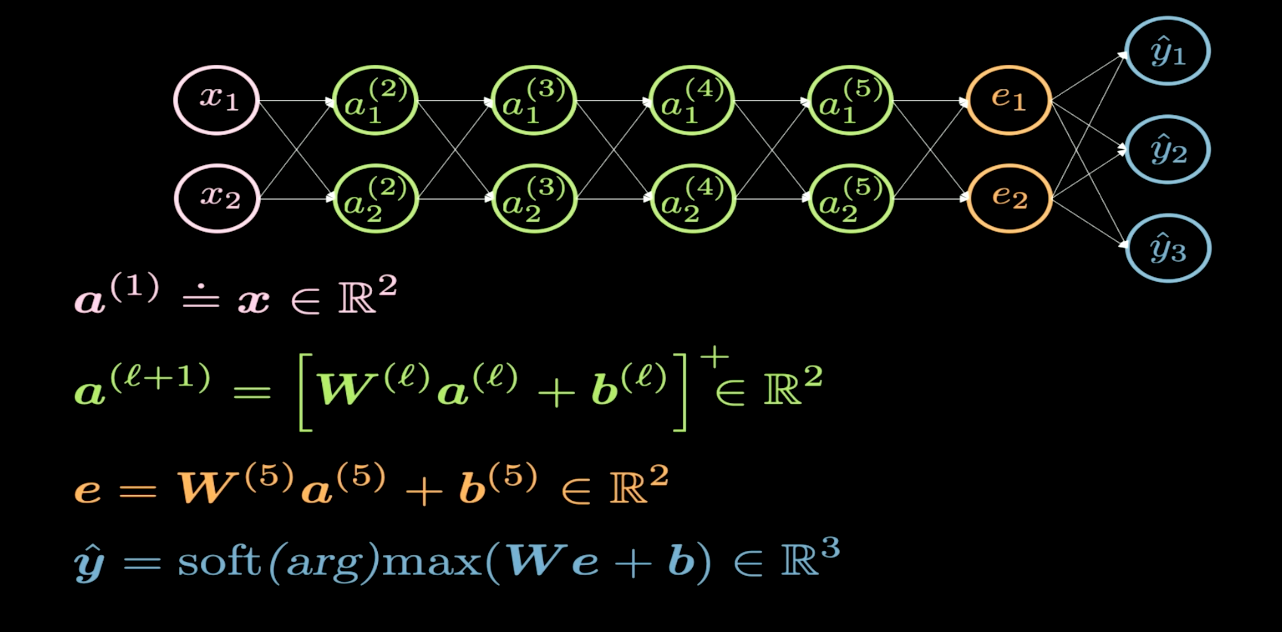
Figure 1 : Structure du réseau

La figure 1 illustre la structure du réseau de neurones que nous souhaitons visualiser. En général, lorsque nous dessinons la structure d’un réseau de neurones, l’entrée apparaît en bas ou à gauche et la sortie apparaît en haut ou à droite. Dans la figure 1, les neurones roses représentent les entrées et les neurones bleus les sorties. Dans ce réseau, nous avons 4 couches cachées (en vert), ce qui signifie que nous avons 6 couches au total (4 couches cachées + 1 couche d’entrée + 1 couche de sortie). Dans ce cas, nous avons 2 neurones par couche cachée et donc la dimension de la matrice de poids ($W$) pour chaque couche est de 2 par 2. Cela s’explique par le fait que nous voulons transformer notre plan d’entrée en un autre plan que nous pouvons visualiser.

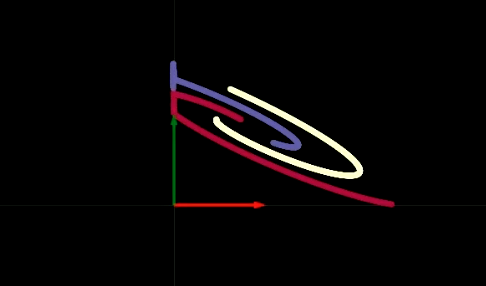
Figure 2 : Visualisation de l'espace de pliage

La transformation de chaque couche est comme le pliage de notre plan dans certaines régions spécifiques, comme le montre la figure 2. Ce pliage est très abrupt, car toutes les transformations sont effectuées dans la couche 2D. Expérimentalement, nous constatons que si nous n’avons que 2 neurones dans chaque couche cachée, l’optimisation prend plus de temps. L’optimisation est plus facile si nous avons davantage de neurones dans les couches cachées. Cela nous laisse avec une question importante à considérer : pourquoi est-il plus difficile d’entraîner le réseau avec moins de neurones dans les couches cachées ?

(a)	(b)

Lorsque nous parcourons le réseau une couche cachée à la fois, nous constatons qu’avec chaque couche, nous effectuons une certaine transformation affine suivie de l’application de l’opération non linéaire ReLU, qui élimine toute valeur négative. Dans les figures 3(a) et (b), nous pouvons voir la visualisation de l’opérateur ReLU. L’opérateur ReLU nous aide à effectuer des transformations non linéaires. Après avoir effectué plusieurs étapes de transformation affine suivies par l’opérateur ReLU, nous sommes finalement en mesure de séparer les données de manière linéaire, comme le montre la figure 4.

Figure 4 : Visualisation des résultats

Elle nous permet de comprendre pourquoi les couches cachées à deux neurones sont plus difficiles à entraîner. Notre réseau à 6 couches a un biais dans chaque couche cachée. Par conséquent, si l’un de ces biais déplace des points hors du quadrant supérieur droit, l’application de l’opérateur ReLU éliminera ces points. Ensuite, quelle que soit la façon dont les couches ultérieures transforment les données, les valeurs resteront nulles. Nous pouvons rendre un réseau de neurones plus facile à entraîner en rendant le réseau plus « gros » (c’est-à-dire en ajoutant plus de neurones dans les couches cachées) ou nous pouvons ajouter d’autres couches cachées, ou une combinaison des deux méthodes.

Transformations des paramètres

La transformation générale des paramètres signifie que notre vecteur de paramètres $w$ est la sortie d’une fonction. Par cette transformation, nous pouvons faire correspondre l’espace de paramètres d’origine à un autre espace. Dans la figure 5, $w$ est en fait la sortie de $H$ avec le paramètre $u$. $G(x,w)$ est un réseau et $C(y,\bar y)$ est une fonction de coût. La formule de rétropropagation est également adaptée comme suit :

Ces formules sont appliquées sous forme de matrice. Les dimensions de $u$,$w$,$\frac{\partial H}{\partial u}^\top$,$\frac{\partial C}{\partial w}^\top$ sont respectivement $[N_u \times 1]$,$[N_w \times 1]$,$[N_u \times N_w]$ et $[N_w \times 1]$. Par conséquent, la dimension de notre formule de rétropropagation est cohérente.

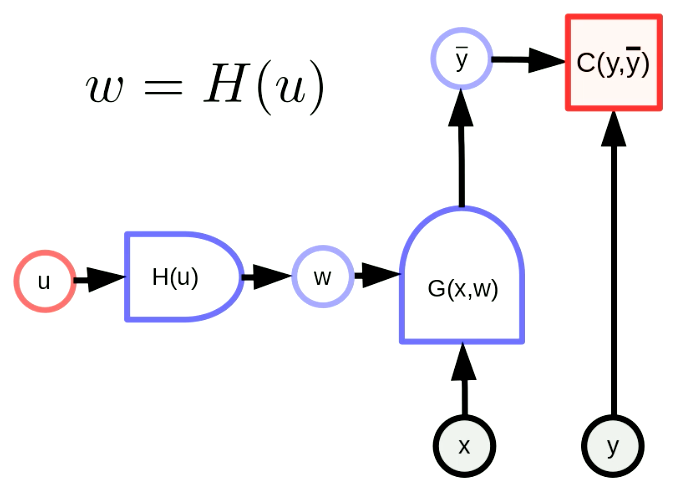
Figure 5 : Forme générale des transformations de paramètres

Une transformation des paramètres simple : le partage des poids

Le partage des poids signifie que $H(u)$ reproduit simplement une composante de $u$ en plusieurs composantes de $w$. $H(u)$ est comme une branche Y pour copier $u_1$ en $w_1$, $w_2$. Cela peut être exprimé sous la forme :

Nous forçons les paramètres partagés à être égaux, de sorte que le gradient par rapport aux paramètres partagés sera additionné dans la rétropropagation. Par exemple, le gradient de la fonction de coût $C(y, \bar y)$ par rapport à $u_1$ sera la somme du gradient de la fonction de coût $C(y, \bar y)$ par rapport à $w_1$ et du gradient de la fonction de coût $C(y, \bar y)$ par rapport à $w_2$.

Hyper-réseau

Un hyper-réseau est un réseau où les poids d’un réseau sont la sortie d’un autre réseau. La figure 6 montre le graphique de calcul d’un hyper-réseau. Ici, la fonction $H$ est un réseau avec le vecteur paramètre $u$ et l’entrée $x$. En conséquence, les poids de $G(x,w)$ sont configurés dynamiquement par le réseau $H(x,u)$. Bien que cette idée soit ancienne, elle reste très puissante.

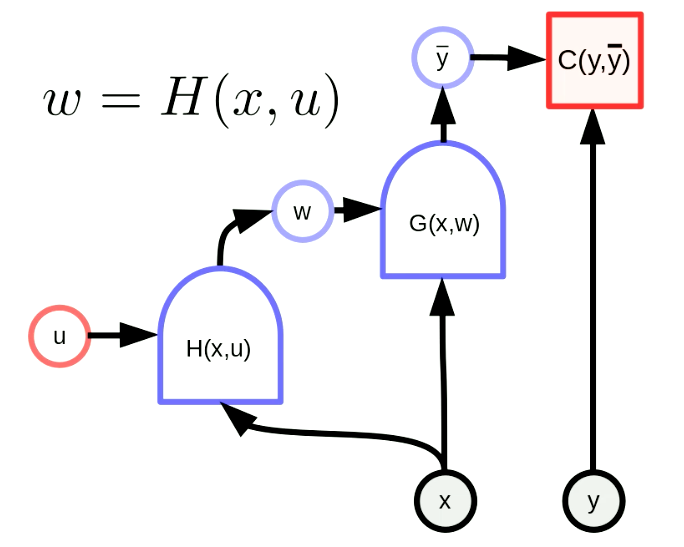
Figure 6 : Hyper-réseau

Détection de motifs dans les données séquentielles

La partage de poids peut être appliqué à la détection de motifs. La détection de motifs consiste à trouver certains motifs dans des données séquentielles comme des mots-clés dans la parole ou le texte. Une façon d’y parvenir, comme le montre la figure 7, consiste à utiliser une fenêtre coulissante sur les données, qui déplace la fonction de partage de poids pour détecter un motif particulier (c’est-à-dire un son particulier dans le signal vocal) et les sorties (c’est-à-dire une partition) passent dans une fonction maximale.

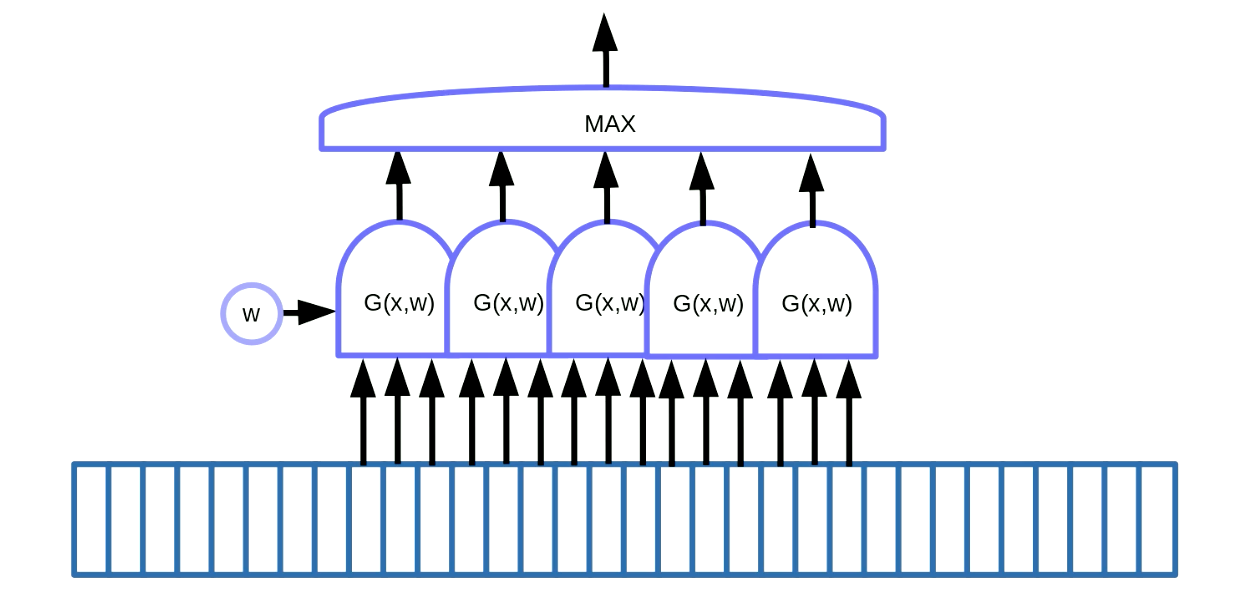
Figure 7 : Détection des motifs pour les données séquentielles

Dans cet exemple, nous avons cinq de ces fonctions. Cette solution nous permet d’additionner cinq gradients et de rétropropager l’erreur pour mettre à jour le paramètre $w$. En implémentant cela dans PyTorch, nous voulons empêcher l’accumulation implicite de ces gradients, donc nous devons utiliser zero_grad() pour initialiser le gradient.

Détection de motifs dans les images

L’autre application utile est la détection de motifs dans les images. Nous faisons généralement glisser nos patrons sur les images pour détecter les formes indépendamment de leur position et de leur distorsion. Un exemple simple consiste à distinguer un « C » d’un « D », comme le montre la figure 8. La différence entre « C » et « D » est que « C » a deux extrémités et « D » a deux coins. Nous pouvons donc concevoir des patrons d’extrémité et des patrons d’angle. Si la forme est similaire aux patrons, les sorties seront limitées. Nous pouvons alors distinguer les lettres de ces sorties en les additionnant. Dans la figure 8, le réseau détecte deux points d’extrémité et zéro coin, donc il active « C ».

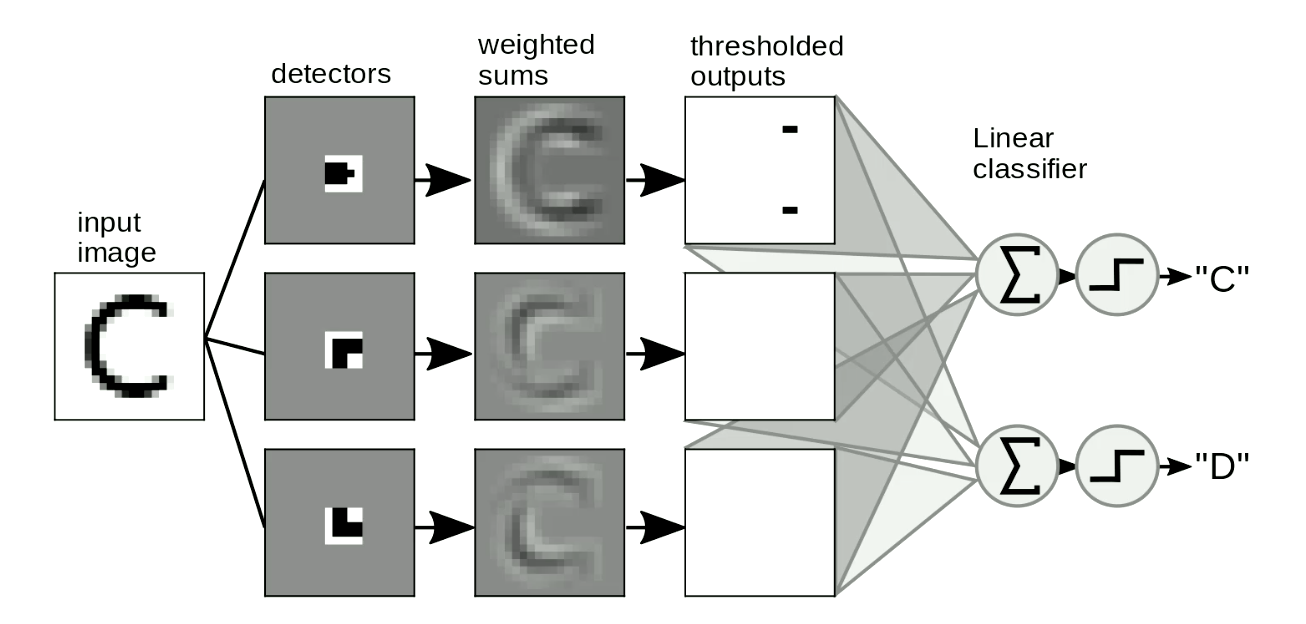
Figure 8 : Détection de motifs pour les images

Il est également important que notre appariement de pochoirs (template matching en anglais) soit invariable par décalage : lorsque nous décalons l’entrée, la sortie (c’est-à-dire la lettre détectée) ne doit pas changer. Ce problème peut être résolu par une transformation de type partage de poids. Comme le montre la figure 9, lorsque nous changeons l’emplacement de « D », nous pouvons toujours détecter les motifs de coin même s’ils sont décalés. Lorsque nous additionnons les motifs, cela active la détection de « D ».

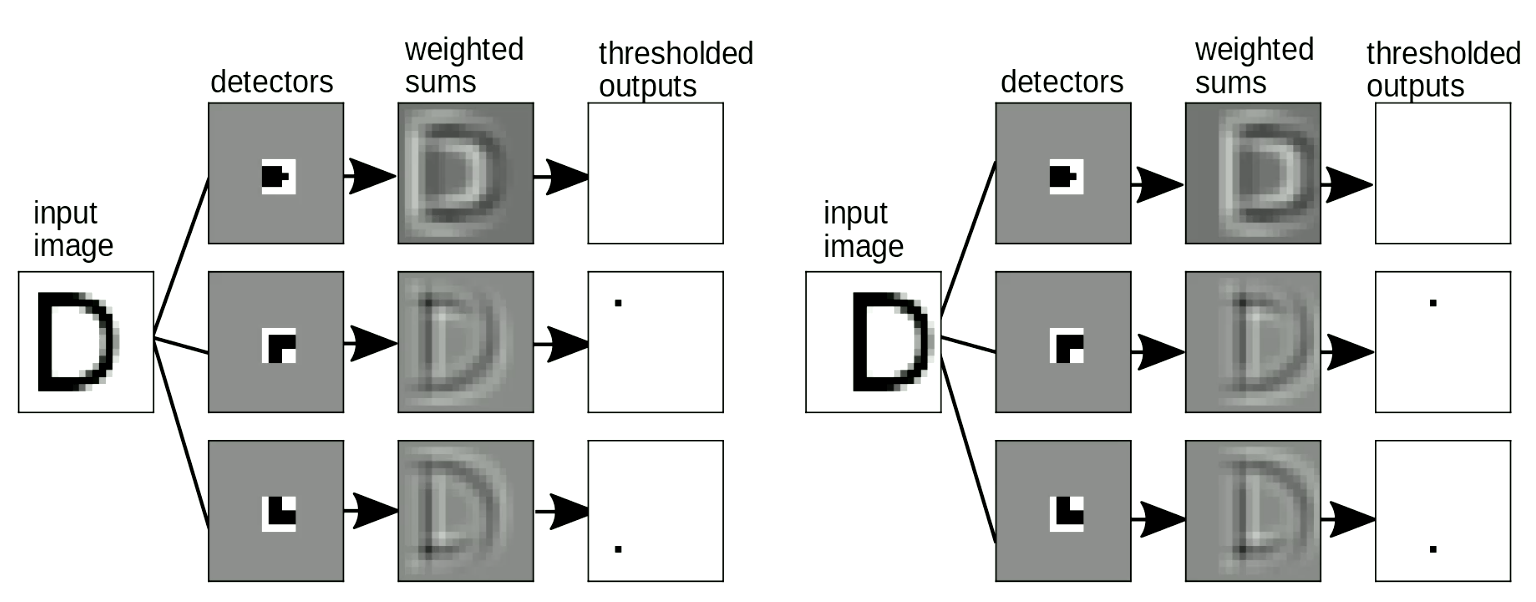
Figure 9 : Invariance aux décalages

Cette méthode artisanale d’utilisation de détecteurs locaux et de sommation pour la reconnaissance des chiffres a été utilisée pendant de nombreuses années. Mais elle nous pose le problème suivant : comment pouvons-nous concevoir ces pochoirs automatiquement ?
Pouvons-nous utiliser des réseaux de neurones pour apprendre ces pochoirs ? Pour cela nous allons introduire le concept de convolutions, c’est-à-dire l’opération que nous utilisons pour faire correspondre les images avec les pochoirs.

Convolution discrète

Convolution

La définition mathématique précise d’une convolution dans le cas unidimensionnel entre l’entrée $x$ et $w$ est :

En d’autres termes, la $i$-ème sortie est calculée comme le produit scalaire entre les $w$ inversés et une fenêtre de même taille en $x$. Pour calculer la sortie complète, on commence avec la fenêtre au début puis on décale cette fenêtre d’une entrée à chaque fois. On répète le procédé jusqu’à ce que $x$ soit épuisé.

Corrélation croisée

En pratique, la convention adoptée dans les frameworks d’apprentissage profond comme PyTorch est légèrement différente. La convolution dans PyTorch est mise en œuvre lorsque $w$ est non inversé :

Les mathématiciens appellent cette formulation « corrélation croisée ». Dans notre contexte, cette différence n’est qu’une différence de convention. En pratique, la corrélation croisée et la convolution peuvent être interchangeables si l’on lit les poids stockés en mémoire en avant ou en arrière.

Il est important d’être conscient de cette différence, par exemple, lorsqu’on veut utiliser certaines propriétés mathématiques de la convolution/corrélation à partir de textes mathématiques.

Convolution de dimensions supérieures

Pour les entrées bidimensionnelles telles que les images, nous utilisons la version bidimensionnelle de la convolution :

Cette définition peut facilement être étendue au-delà de deux dimensions à trois ou quatre dimensions. Ici, $w$ est appelé le noyau de convolution.

Les torsions de base qui peuvent être réalisées avec l’opérateur convolutif dans les ConvNets profonds

• Décalage (striding) : au lieu de décaler la fenêtre en $x$ une entrée à la fois, on peut le faire avec un pas plus grand (par exemple deux ou trois entrées à la fois). Exemple : supposons que l’entrée $x$ soit unidimensionnelle et ait une taille de $100$ et que $w$ ait une taille de $5$. La taille de la sortie avec un pas de $1$ ou $2$ est indiquée dans le tableau ci-dessous :

• Remplissage (padding) : très souvent, dans la conception des architectures de réseaux neuronaux profonds, nous voulons que la sortie de la convolution soit de la même taille que l’entrée. Cela peut être réalisé en ajoutant aux extrémités de l’entrée un certain nombre d’entrées (généralement) nulles, généralement des deux côtés. Le remplissage se fait surtout par commodité. Il peut parfois avoir un impact sur les performances et entraîner d’étranges effets de bord, cela dit, lorsqu’on utilise une non-linéarité ReLU, le remplissage avec des zéros n’est pas déraisonnable.

ConvNets profonds

Comme décrit précédemment, les réseaux neuronaux profonds sont généralement organisés sous forme d’alternance répétée entre des opérateurs linéaires et des couches de non-linéarité ponctuelles. Dans les réseaux neuronaux convolutifs, l’opérateur linéaire sera l’opérateur de convolution décrit ci-dessus. Il existe également un troisième type de couche optionnelle appelée couche d’agrégation (pooling layer).

La raison de l’empilement de plusieurs couches de ce type est que nous voulons construire une représentation hiérarchique des données. Les ConvNets ne doivent pas être limités au traitement des images, ils ont également été appliqués avec succès à la parole et au langage. Techniquement, ils peuvent être appliqués à tout type de données qui se présentent sous la forme de tableaux, bien que nous ayons également ces tableaux pour satisfaire certaines propriétés.

Pourquoi voudrions-nous saisir la représentation hiérarchique du monde ? Parce que le monde dans lequel nous vivons est compositionnel. Ce point est évoqué dans les sections précédentes. Cette nature hiérarchique peut être observée à partir du fait que les pixels locaux s’assemblent pour former des motifs simples tels que des bords orientés. Ces bords sont à leur tour assemblés pour former des caractéristiques locales telles que des coins, des jonctions en T, etc. Ces bords sont assemblés pour former des motifs encore plus abstraits. Ces bords sont assemblés pour former des motifs encore plus abstraits. Nous pouvons continuer à nous appuyer sur ces représentations hiérarchiques pour finalement former les objets que nous observons dans le monde réel.

Figure 10 : Visualisation des caractéristiques d'un réseau convolutif entraîné sur ImageNet d'après Zeiler & Fergus (2013)

Cette nature compositionnelle et hiérarchique que nous observons dans le monde naturel n’est donc pas seulement le résultat de notre perception visuelle, mais est aussi vraie au niveau physique. Au niveau le plus bas de la description, nous avons des particules élémentaires, qui s’assemblent pour former des atomes, les atomes forment ensemble des molécules, nous continuons à nous appuyer sur ce processus pour former des matériaux, des parties d’objets et finalement des objets complets dans le monde physique.

La nature compositionnelle du monde pourrait être la réponse à la question rhétorique d’Einstein sur la façon dont les humains comprennent le monde dans lequel ils vivent : « La chose la plus incompréhensible à propos de l’univers est qu’il est compréhensible ».

Le fait que les humains comprennent le monde grâce à cette nature compositionnelle semble être une conspiration pour Yann. Il avance que sans cette compositionnalité, il faudrait encore plus de magie pour que les humains comprennent le monde dans lequel ils vivent. Il cite le mathématicien Stuart Geman : « Le monde est composé ou Dieu existe ».

Inspirations de la biologie

Alors pourquoi l’apprentissage profond devrait-il être ancré dans l’idée que notre monde est compréhensible et a une nature compositionnelle ? Les recherches menées par Simon Thorpe ont contribué à motiver cette idée. Il a montré que la façon dont nous reconnaissons les objets quotidiens est extrêmement rapide. Ses expériences ont consisté à faire clignoter un ensemble d’images toutes les 100 ms, puis à demander aux utilisateurs d’identifier ces images, ce qu’ils ont réussi à faire. Cela a montré qu’il faut environ 100 ms aux humains pour détecter des objets. En outre, le diagramme ci-dessous illustre des parties du cerveau annotées du temps que mettent les neurones à se propager d’une zone à l’autre :

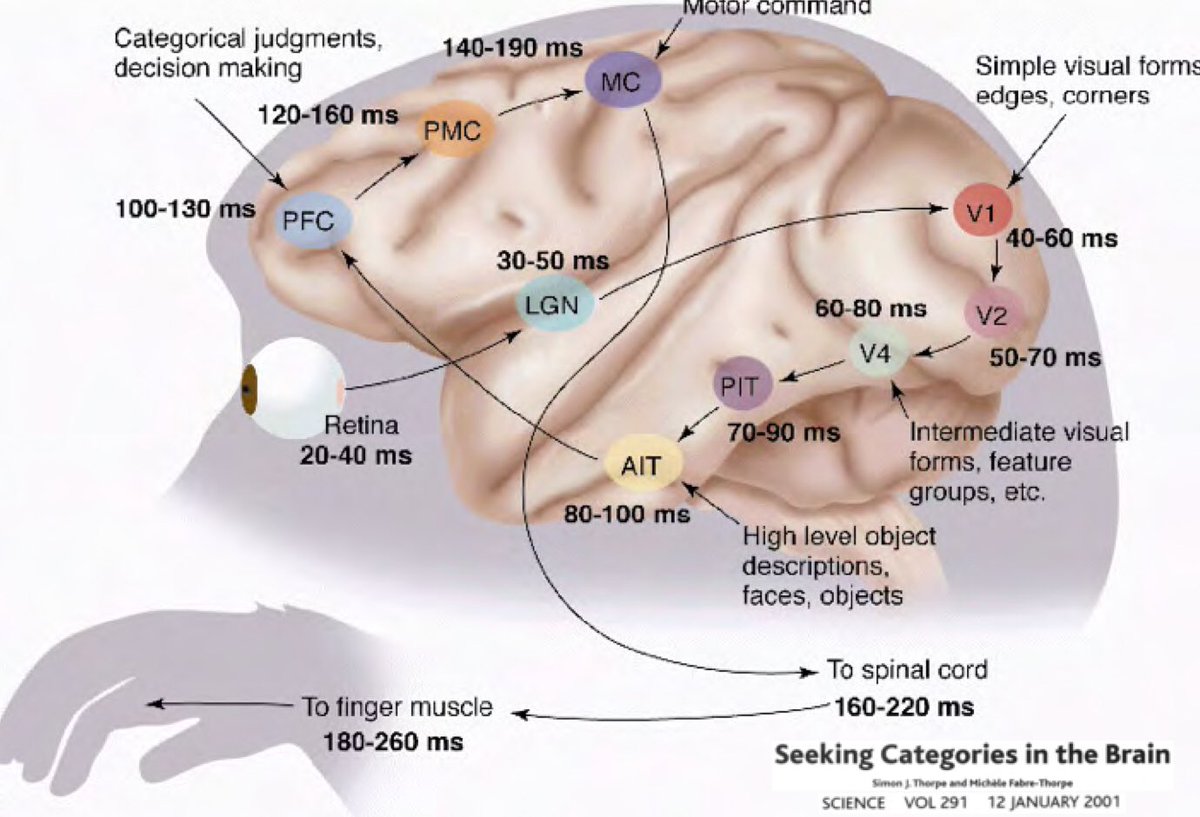
Les signaux passent de la rétine au corps géniculé latéral (LGN sur la figure 11) qui aide à l’amélioration du contraste, au contrôle des portes, etc., puis au cortex visuel primaire V1, V2, V4, puis au cortex inférotemporel (PIT), qui est la partie du cerveau où les catégories sont définies. Les observations en chirurgie à cerveau ouvert ont montré que si vous montrez un film à un humain, les neurones du PIT ne se déclenchent que lorsqu’ils détectent certaines images (comme Jennifer Aniston ou la grand-mère d’une personne par exemple) et rien d’autre. Les déclenchements neuronaux sont invariables en fonction de la position, de la taille, de l’éclairage, de l’orientation de votre grand-mère, de ce qu’elle porte, etc.

De plus, le temps de réaction extrêmement rapide avec lequel les humains ont pu classer ces éléments (à peine assez de temps pour que quelques décharges passent) démontre qu’il est possible de le faire sans passer de temps supplémentaire sur des calculs complexes et récurrents. Il s’agit plutôt d’un processus feed-forward unique.

Ces idées ont suggéré que nous pourrions développer une architecture de réseau neuronal qui soit complètement feed-forward, tout en étant capable de résoudre le problème de la reconnaissance, d’une manière qui soit invariante aux transformations non pertinentes de l’entrée.

Gallant & Van Essen, dont le modèle du cerveau humain illustre deux voies distinctes, nous donnent un autre aperçu de ce dernier :

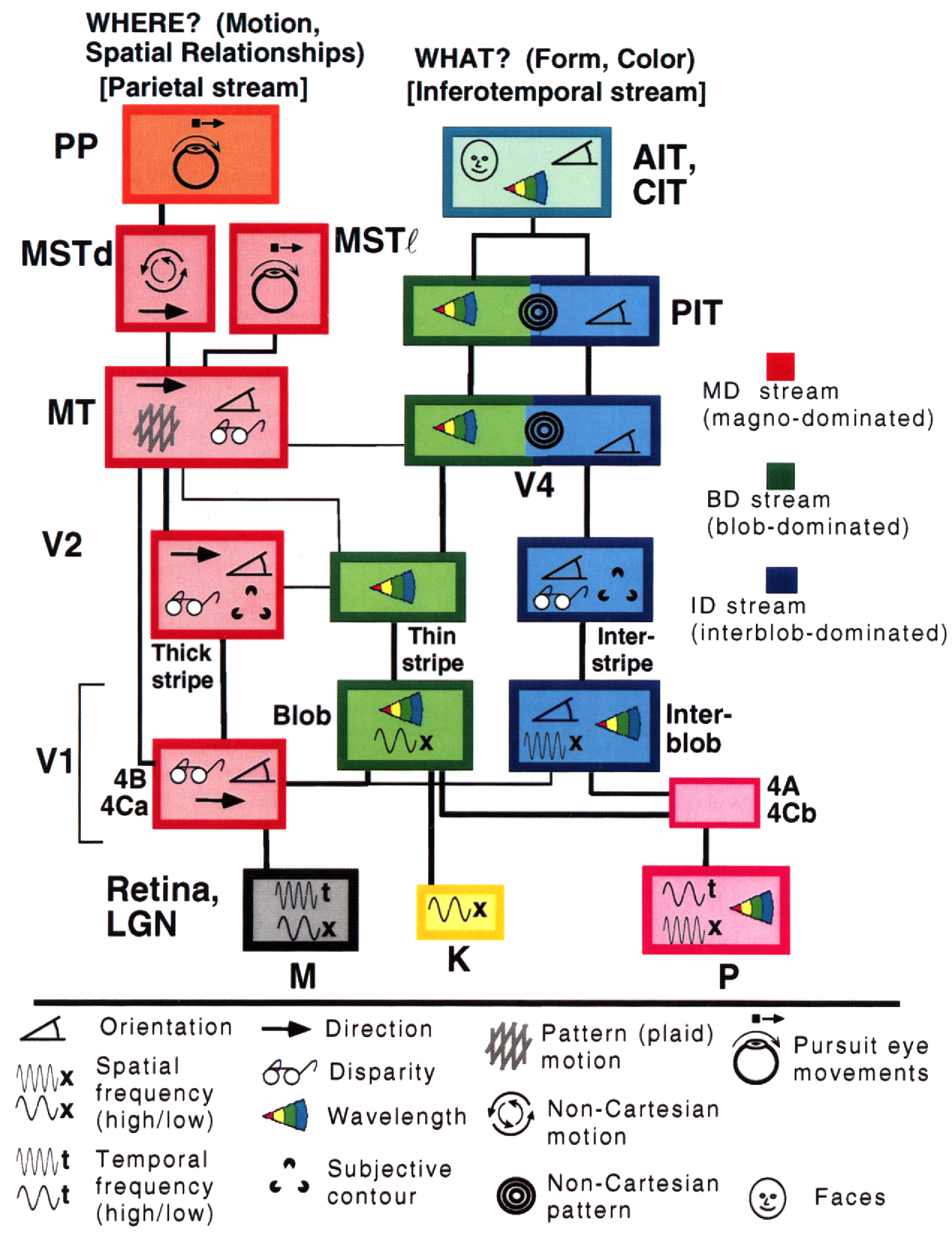
Le côté droit montre la voie ventrale, qui vous indique ce que vous regardez, tandis que le côté gauche montre la voie dorsale, qui identifie les emplacements, la géométrie et le mouvement. Ils semblent assez séparés dans le cortex visuel de l’homme et des primates (avec quelques interactions entre eux bien sûr).

Les contributions de Hubel & Weisel (1962)

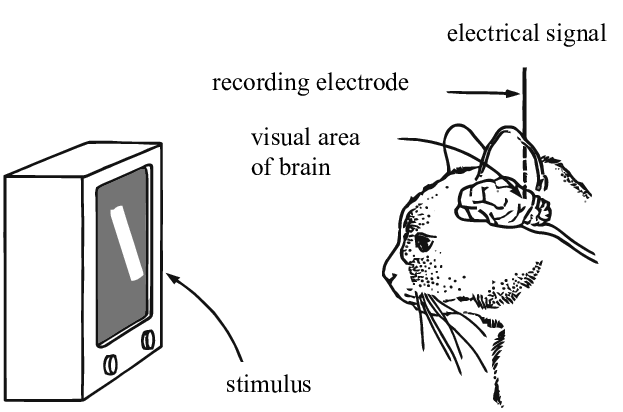
Dans leurs expériences, Hubel et Weisel ont utilisé des électrodes pour mesurer les tirs neuronaux dans le cerveau des chats en réponse à des stimuli visuels. Ils ont découvert que les excitations neuronales de la région V1 ne sont sensibles qu’à certaines zones d’un champ visuel (appelées champs réceptifs) et détectent des bords orientés dans cette zone. Par exemple, ils ont démontré que si on montre au chat une barre verticale et commençons à la faire tourner, le neurone se déclenchera à un angle particulier. De même, à mesure que la barre s’éloigne de cet angle, l’activation du neurone diminue. Ces neurones à activation sélective, Hubel & Weisel les ont nommés « cellules simples » pour leur capacité à détecter des caractéristiques locales.

Ils ont également découvert que si on déplace la barre hors du champ de réception, ce neurone particulier ne s’active plus, mais un autre neurone le fera. Il existe des détecteurs de caractéristiques locales correspondant à toutes les zones du champ visuel, d’où l’idée que le cerveau humain traite les informations visuelles comme un ensemble de convolutions.

Un autre type de neurone, qu’ils ont appelé « cellules complexes », regroupe la sortie de plusieurs cellules simples dans une certaine zone. On peut considérer qu’elles calculent un agrégat des activations en utilisant une fonction telle que maximum, somme, somme des carrés, ou toute autre fonction ne dépendant pas de l’ordre. Ces cellules complexes détectent les bords et les orientations dans une région, indépendamment de l’endroit où ces stimuli se trouvent spécifiquement dans la région. En d’autres termes, elles sont invariantes par rapport aux petites variations de positions de l’entrée.

Les contributions de Fukushima (1982)

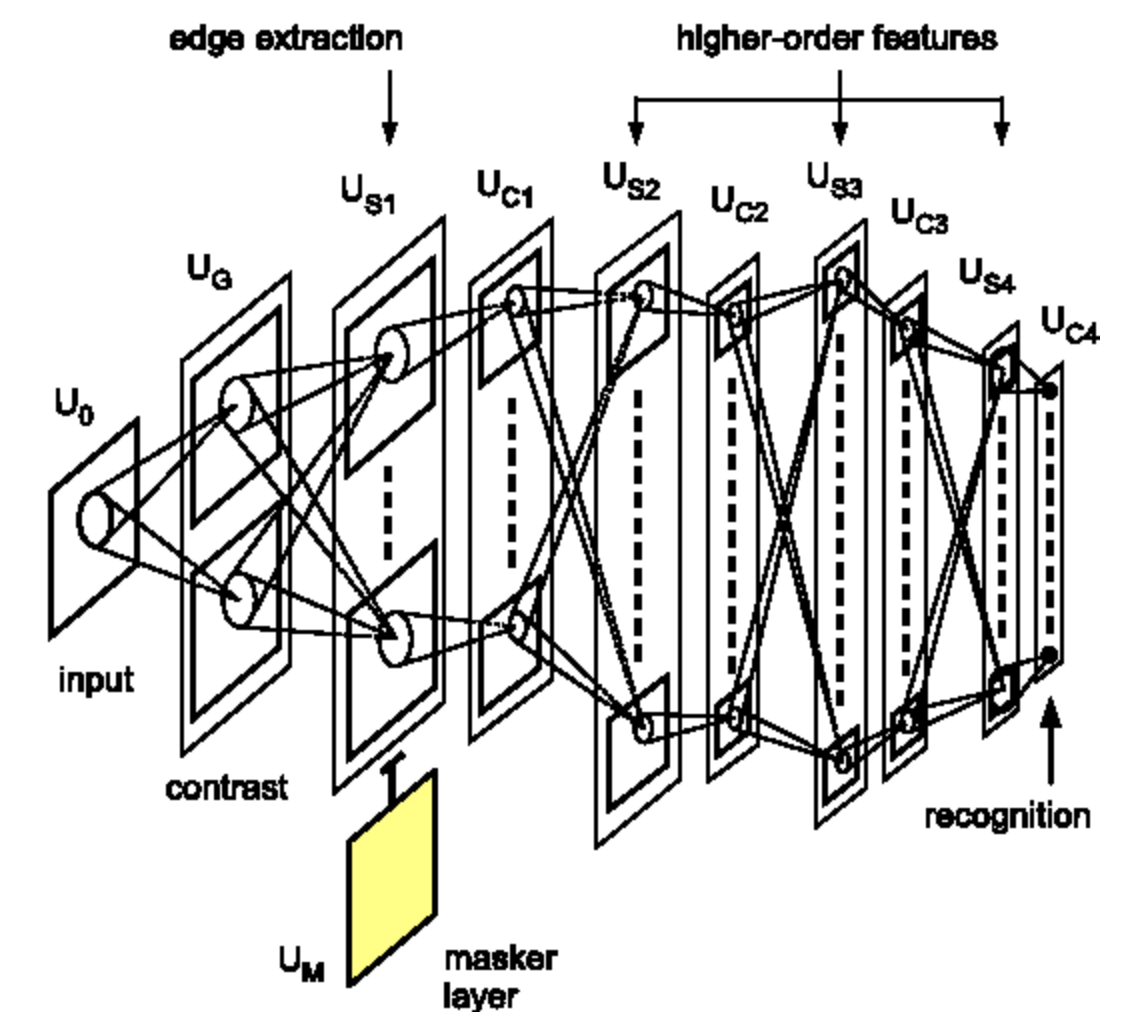
Fukushima a été le premier à mettre en œuvre, avec des modèles informatiques, l’idée de couches multiples de cellules simples et de cellules complexes. Certains de ces détecteurs de caractéristiques ont été fabriqués à la main ou appris, bien que l’apprentissage ait utilisé des algorithmes de clustering non supervisés, entraînés séparément pour chaque couche, car la rétropropagation n’était pas encore utilisée. Yann Le Cun est arrivé quelques années plus tard (1989 et 1998) et a mis en place la même architecture, mais cette fois-ci, avec un entraînement supervisé utilisant la rétropropagation. Cette méthode est largement considérée comme la genèse des réseaux neuronaux convolutifs modernes. A noter que Riesenhuber du MIT a également redécouvert cette architecture en 1999, bien qu’il n’ait pas utilisé la rétropropagation.