Calcul des gradients pour les modules des réseaux de neurones et astuces pratiques pour la rétropropagation

Un exemple concret de rétropropagation et d’introduction aux modules de base des réseaux neuronaux

Exemple

Nous considérons un exemple concret de rétropropagation à l’aide d’une représentation graphique. La fonction arbitraire $G(w)$ est introduite dans la fonction de coût $C$, qui peut être représentée sous forme d’un graphe. Par la manipulation de la multiplication des matrices jacobiennes, nous pouvons transformer ce graphe en un qui calculera les gradients à l’envers. Notez que PyTorch et TensorFlow font cela automatiquement pour l’utilisateur, c’est-à-dire que le graphe de la propagation avant est automatiquement « inversé » pour créer le graphe dérivé qui rétropropage le gradient.

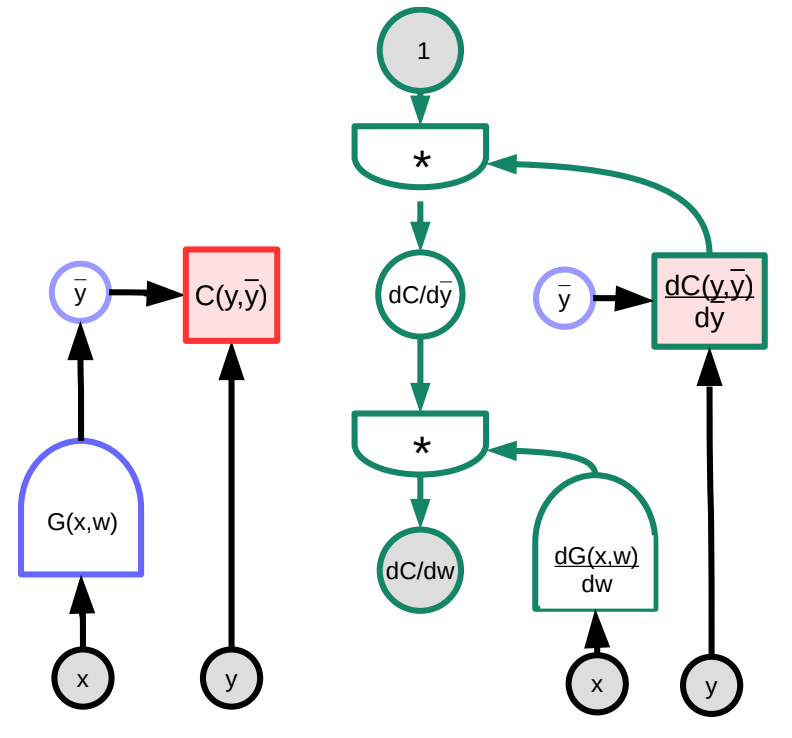Figure 1 : Illustration graphique de la rétropropagation

Dans cet exemple, le graphe vert à droite représente le gradient. En suivant le graphe à partir du nœud supérieur, il s’ensuit que :

\(\frac{\partial C(y,\bar{y})}{\partial w}=1 \cdot \frac{\partial C(y,\bar{y})}{\partial\bar{y}}\cdot\frac{\partial G(x,w)}{\partial w}\)

En termes de dimensions :

• $\frac{\partial C(y,\bar{y})}{\partial w}$ est un vecteur ligne de taille $1\times N$ où $N$ est le nombre de composantes de $w$
• $\frac{\partial C(y,\bar{y})}{\partial \bar{y}}$ est un vecteur ligne de taille $1\times M$, où $M$ est la dimension de la sortie
• $\frac{\partial \bar{y}}{\partial w}=\frac{\partial G(x,w)}{\partial w}$ est une matrice de taille $M\times N$, où $M$ est le nombre de sorties de $G$ et $N$ est la dimension de $w$.

Des complications peuvent survenir lorsque l’architecture du graphe n’est pas fixe mais dépend des données. Par exemple, nous pourrions choisir un module de réseau neuronal en fonction de la longueur du vecteur d’entrée. Bien que cela soit possible, cela devient de plus en plus difficile de gérer cette variation lorsque le nombre de boucles dépasse un montant raisonnable.

Modules de base des réseaux neuronaux

Il existe différents types de modules préconstruits en plus des modules Linear et ReLU bien connus. Ils sont utiles car ils sont optimisés de manière unique pour remplir leurs fonctions respectives (par opposition à une combinaison d’autres modules élémentaires).

• Linear : $Y=W\cdot X$

  \[\begin{aligned} \frac{dC}{dX} &= W^\top \cdot \frac{dC}{dY} \\ \frac{dC}{dW} &= \frac{dC}{dY} \cdot X^\top \end{aligned}\]

• ReLU : $y=(x)^+$

  \[\frac{dC}{dX} = \begin{cases} 0 & x<0\\ \frac{dC}{dY} & \text{ else} \end{cases}\]

• Dupliquer : $Y_1=X$, $Y_2=X$

  • semblable à un “Y - splitter” où les deux sorties sont égales à l’entrée.

  • en rétropropagation, les gradients sont additionnés

  • peut être divisé en $n$ branches : $ \frac{dC}{dX}=\frac{dC}{dY_1}+\frac{dC}{dY_2}$

• Ajouter : $Y=X_1+X_2$

  • en additionnant deux variables, lorsque l’une d’entre elles est perturbée, la sortie sera perturbée par la même quantité, c’est-à-dire :

    \[\frac{dC}{dX_1}=\frac{dC}{dY}\cdot1 \quad \text{et}\quad \frac{dC}{dX_2}=\frac{dC}{dY}\cdot1\]

• Max : $Y=\max(X_1,X_2)$

  • cette fonction peut également être représentée comme :

    \[Y=\max(X_1,X_2)=\begin{cases} X_1 & X_1 > X_2 \\\\ X_2 & \text{else} \end{cases} \Rightarrow \frac{dY}{dX_1}=\begin{cases} 1 & X_1 > X_2 \\\\ 0 & \text{else} \end{cases}\]

  • donc, par la règle de la chaîne :

    \[\frac{dC}{dX_1}=\begin{cases} \frac{dC}{dY}\cdot1 & X_1 > X_2 \\ 0 & \text{sinon} \end{cases}\]

La fonction LogSoftMax vs la fonction SoftMax

SoftMax, qui est également un module PyTorch, est un moyen pratique de transformer un groupe de nombres en un groupe de nombres positifs entre $0$ et $1$ dont la somme vaut 1. Ces nombres peuvent être interprétés comme une distribution de probabilité. Par conséquent, il est couramment utilisé dans les problèmes de classification. $y_i$ dans l’équation ci-dessous est un vecteur de probabilités pour toutes les catégories.

Cependant, l’utilisation de SoftMax laisse la possibilité que les gradients disparaissent dans le réseau. La disparition du gradient est un problème, car elle empêche les poids en aval d’être modifiés par le réseau neuronal, ce qui peut empêcher complètement l’entraînement du réseau neuronal. La fonction sigmoïde logistique, qui est la fonction softmax pour une valeur, montre que lorsque $s$ est grand, $h(s)$ vaut $1$, et lorsque s est petit, $h(s)$ vaut $0$. Comme la fonction sigmoïde est plate à $h(s) = 0$ et $h(s) = 1$, le gradient est de $0$, ce qui se traduit par un gradient qui disparaît.

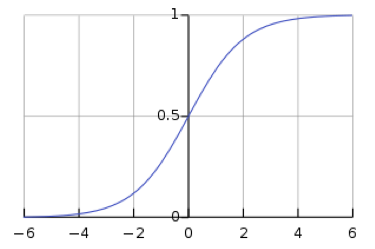Figure 2 : La fonction sigmoïde

Les mathématiciens ont eu l’idée de la fonction LogSoftMax afin de résoudre le problème de disparition du gradient créé par la fonction SoftMax. LogSoftMax est un autre module de base de PyTorch. Comme on peut le voir dans l’équation ci-dessous, LogSoftMax est une combinaison de softmax et du log.

L’équation ci-dessous montre une autre façon de considérer la même équation. La figure ci-dessous montre la partie $\log(1 + \exp(s))$ de la fonction. Lorsque $s$ est très petit, la valeur est $0$, et lorsque $s$ est très grand, la valeur est $s$. Par conséquent, elle ne sature pas et le problème du gradient disparaît.

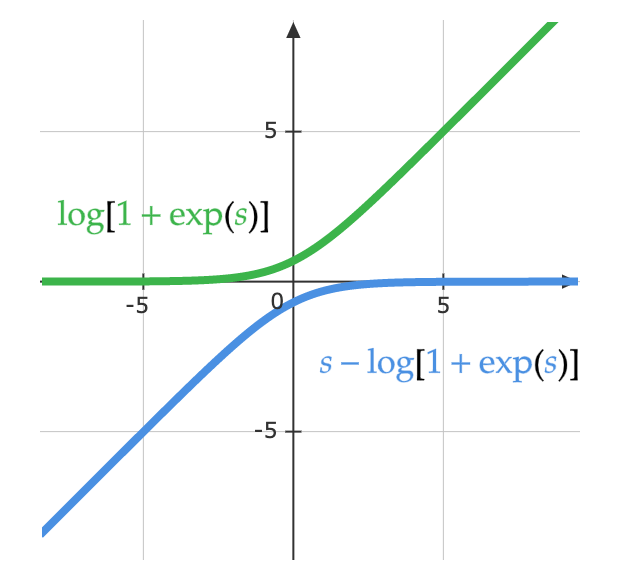
Astuces pour la rétropropagation

Utiliser ReLU comme fonction d’activation non linéaire

ReLU fonctionne mieux pour les réseaux à plusieurs couches, ce qui a fait que des alternatives comme la fonction sigmoïde et la fonction tangente hyperbolique $\tanh(\cdot)$ ont perdu de leur popularité. La raison pour laquelle ReLU fonctionne le mieux est probablement due à son unique nœud qui le rend d’échelle équivalente.

Utiliser la perte d’entropie croisée comme fonction objectif pour les problèmes de classification

La fonction logsoftmax, dont nous avons parlé plus tôt, est un cas particulier de l’entropie croisée. Dans PyTorch, il faut mieux s’assurer de fournir la fonction de perte d’entropie croisée avec logsoftmax comme entrée (par opposition à la softmax normale).

Utiliser la descente de gradient stochastique sur les minibatchs pendant l’entraînement

Comme nous l’avons vu précédemment (voir la page web Introduction à la descente de gradient et à l’algorithme de rétropropagation), les minibatchs permettent d’entraîner plus efficacement car utilisent la redondance des données. Cela évite d’avoir besoin de faire une prédiction et de calculer la perte sur chaque observation à chaque étape pour estimer le gradient.

Mélanger l’ordre des exemples d’entraînement lorsque vous utilisez la descente stochastique

L’ordre est important. Si le modèle ne voit que des exemples d’une seule classe à chaque étape de l’entraînement, il apprendra à prédire cette classe sans savoir pourquoi il devrait le faire. Par exemple, si vous essayez de classer des chiffres du jeu de données MNIST et que les données ne sont pas mélangées, les paramètres de biais dans la dernière couche prédiraient simplement toujours zéro, puis s’adapteraient pour toujours prédire un, puis deux, etc. Idéalement, il faut avoir des échantillons de chaque classe dans chaque minibatch.

Cependant, le débat se poursuit pour savoir s’il faut changer l’ordre des échantillons à chaque passage (époque).

Normaliser les entrées pour avoir une moyenne nulle et une variance de 1

Avant d’entraîner, il est utile de normaliser chaque caractéristique d’entrée afin qu’elle ait une moyenne de zéro et un écart-type de un. Lors de l’utilisation de données d’images RVB, il est courant de prendre la moyenne et l’écart-type de chaque canal individuellement et de normaliser l’image par canal. Par exemple, prendre la moyenne $m_b$ et l’écart-type $\sigma_b$ de toutes les valeurs du bleu dans l’ensemble de données, puis normaliser les valeurs du bleu pour chaque image individuelle comme

où $\epsilon$ est un nombre arbitrairement petit que nous utilisons pour éviter la division par zéro. Il faut alors répéter la même chose pour les canaux verts et rouges.
Ceci est nécessaire pour obtenir un signal significatif à partir d’images prises sous différents éclairages. Par exemple, les images prises en plein jour contiennent beaucoup de rouge alors que les images sous-marines n’en contiennent presque pas.

Utiliser un schéma pour diminuer le taux d’apprentissage

Le taux d’apprentissage devrait diminuer au fur et à mesure de l’entraînement. En pratique, la plupart des modèles avancés sont entraînés en utilisant des algorithmes comme Adam qui adaptent le taux d’apprentissage au lieu d’une simple SGD avec un taux d’apprentissage constant.

Utiliser la régularisation L1 et/ou L2 pour le taux de décroissance des poids

Il est possible d’ajouter un coût pour les poids importants à la fonction de coût. Par exemple, en utilisant la régularisation L2, nous définirions la perte $L$ et mettrions à jour les pondérations $w$ comme suit :

Pour comprendre pourquoi on appelle cela le taux de décroissance des poids (weight decay en anglais), notez que nous pouvons réécrire la formule ci-dessus pour montrer que nous multiplions $w_i$ par une constante inférieure à un pendant la mise à jour :

La régularisation L1 (Lasso) est similaire, sauf que nous utilisons $\sum_i \vert w_i\vert$ au lieu de $\Vert w \Vert^2$.

Essentiellement, la régularisation essaie de dire au système de minimiser la fonction de coût avec le vecteur de poids le plus court possible. Avec la régularisation L1, les poids qui ne sont pas utiles sont mis à $0$.

Initialisation des poids

Les poids doivent être initialisés au hasard, mais ils ne doivent pas être trop grands ou trop petits pour que la sortie soit à peu près de la même variance que l’entrée. PyTorch comporte plusieurs astuces d’initialisation des poids. Une des astuces qui fonctionne bien pour les modèles profonds est l’initialisation de Kaiming où l’écart-type des poids est inversement proportionnel à la racine carrée du nombre d’entrées.

Utiliser le dropout

Le dropout est une autre forme de régularisation. Il peut être considéré comme une autre couche du réseau neuronal : il prend les entrées, met aléatoirement à zéro $n/2$ des entrées, et renvoie le résultat en sortie. Cela oblige le système à prendre des informations de toutes les unités d’entrée plutôt que de devenir trop dépendant d’un petit nombre d’unités d’entrée, répartissant ainsi les informations sur toutes les unités d’une couche. Cette méthode a été initialement proposée par Hinton et al. (2012).

Pour plus d’astuces, voir Le Cun et al. (1998). Enfin, notez que la rétropropagation ne fonctionne pas seulement pour les modèles empilés. Elle peut fonctionner pour tout graphe acyclique dirigé (DAG de l’anglais pour directed acyclic graph) tant qu’il y a un ordre partiel sur les modules.