Motivation du problème, algèbre linéaire et visualisation

Ressources

Nous vous invitons à suivre Alfredo Canziani sur Twitter @alfcnz. Vous trouverez sur son compte des vidéos et des manuels contenant des détails pertinents sur l’algèbre linéaire et la décomposition en valeurs singulières (SVD). Ce contenu est trouvable en effectuant une recherche (en anglais) sur le Twitter d’Alfredo, en tapant par exemple linear algebra (from:alfcnz) dans la barre de recherche.

Transformations et motivation

À titre d’exemple, considérons la classification d’images. Supposons que nous prenons une photo avec un appareil photo de $1$ mégapixel. Cette image aura environ $1 000$ pixels verticalement et $1 000$ pixels horizontalement. De plus chaque pixel aura trois dimensions de couleur pour le rouge, le vert et le bleu (RVB). Chaque image peut donc être considérée comme un point dans un espace à $3$ millions de dimensions. Avec une telle dimensionnalité, de nombreuses images intéressantes que nous pourrions vouloir classer, comme un chien ou un chat, se trouveront essentiellement dans la même région de l’espace.

Afin de séparer efficacement ces images, nous envisageons des moyens de transformer les données afin de déplacer les points. Rappelons que dans l’espace bidimensionnel, une transformation linéaire équivaut à une multiplication matricielle. Par exemple, les transformations suivantes peuvent être obtenues en changeant les caractéristiques de la matrice :

• Rotation : lorsque la matrice est orthonormée.
• Mise à l’échelle (« scalabilité ») : lorsque la matrice est diagonale.
• Réflexion : lorsque le déterminant est négatif.
• Shearing.
• Translation.

Notez que la translation seule n’est pas linéaire puisque $0$ ne sera pas toujours mis en correspondance avec $0$, mais c’est une transformation affine. Pour revenir à notre exemple d’image, nous pouvons transformer les points de données en les translatant de manière à ce qu’ils soient regroupés autour de 0 et en les mettant à l’échelle à l’aide d’une matrice diagonale de manière à effectuer un « zoom avant » sur cette région. Enfin, nous pouvons effectuer une classification en trouvant des lignes dans l’espace qui séparent les différents points dans leurs classes respectives. En d’autres termes, l’idée est d’utiliser des transformations linéaires et non linéaires pour représenter les points dans un espace tel qu’ils soient linéairement séparables. Cette idée est rendue plus concrète dans les sections suivantes.

Visualisation des données : séparation des points à l’aide d’un réseau

Dans notre visualisation, nous avons cinq branches d’une spirale, chaque branche correspondant à une couleur différente. Les points vivent dans un plan bidimensionnel et peuvent être représentés sous la forme d’un tuple. La couleur représente une troisième dimension qui peut être considérée comme les différentes classes pour chacun des points. Nous utilisons ensuite le réseau pour séparer chacun des points par couleur.

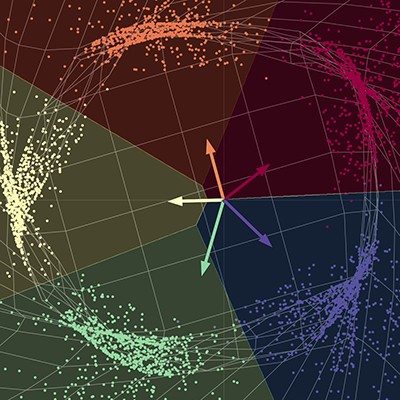(a) Points d’entrée, pré-réseau	(b) Points de sortie, post-réseau

Le réseau « étire » le tissu spatial afin de séparer chacun des points en différents sous-espaces. À la convergence, le réseau sépare chacune des couleurs en différents sous-espaces de la surface finale. En d’autres termes, chacune des couleurs dans ce nouvel espace sera linéairement séparable par une régression « un contre tous ». Les vecteurs du diagramme peuvent être représentés par une matrice de $5 \times 2$. Cette matrice peut être multipliée à chaque point pour obtenir des scores pour chacune des cinq couleurs. Chacun des points peut ensuite être classé par couleur en utilisant les scores respectifs. Ici, la dimension de sortie est de cinq, une pour chacune des couleurs, et la dimension d’entrée est de deux, une pour les coordonnées $x$ et $y$ de chacun des points. Pour résumer, ce réseau prend le tissu spatial et effectue une transformation de l’espace paramétrée par plusieurs matrices puis par des non-linéarités.

Architecture du réseau

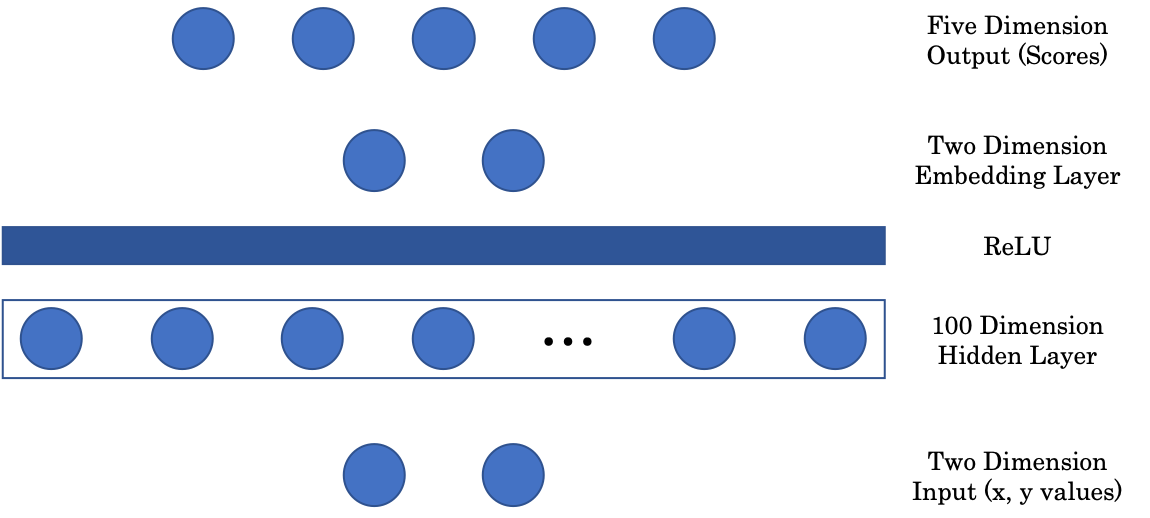
Figure 2 : Architecture du réseau (se lit de bas en haut)

La première matrice fait correspondre l’entrée bidimensionnelle à une couche cachée intermédiaire à $100$ dimensions. Nous avons ensuite une couche non linéaire, ReLU (Rectified Linear Unit), qui est simplement une fonction partie positive $(\cdot)^+$. Ensuite, pour afficher notre image dans une représentation graphique, nous incluons une couche de représentation vectorielle qui fait correspondre l’entrée de la couche cachée à $100$ dimensions à une sortie bidimensionnelle. Enfin, la couche est projetée sur la couche finale à cinq dimensions du réseau, représentant un score pour chaque couleur.

Projections aléatoires : notebook Jupyter

La version anglaise du notebook Jupyter peut être consultée ici. Celle en français est disponible ici. Pour le faire fonctionner, assurez-vous que l’environnement pDL est installé comme indiqué dans le fichier README.md.

PyTorch

PyTorch peut fonctionner à la fois sur le CPU et le GPU d’un ordinateur. Le CPU est utile pour les tâches séquentielles, tandis que le GPU est utile pour les tâches parallèles. Avant d’exécuter sur l’appareil désiré, nous devons d’abord nous assurer que nos tenseurs et modèles sont transférés dans la mémoire de l’appareil. Cela peut être fait avec les deux lignes de code suivantes :

device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
X = torch.randn(n_points, 2).to(device)

La première ligne crée une variable, appelée device, qui est assignée au GPU s’il y en a un de disponible, sinon elle est assignée par défaut au CPU. À la ligne suivante, un tenseur est créé et envoyé à la mémoire du périphérique en appelant .to(device).

Astuce pour les notebooks Jupyter

Pour voir la documentation d’une fonction dans une cellule du notebook, utilisez Shift + Tab.

Visualisation des transformations linéaires

Rappelons qu’une transformation linéaire peut être représentée sous forme de matrice. En utilisant la décomposition en valeur singulière, nous pouvons décomposer cette matrice en trois matrices composantes, chacune représentant une transformation linéaire différente.

Dans l’équation (1), les matrices $U$ et $V^\top$ sont orthogonales et représentent les transformations de rotation et de réflexion. La matrice du milieu est diagonale et représente une transformation d’échelle.

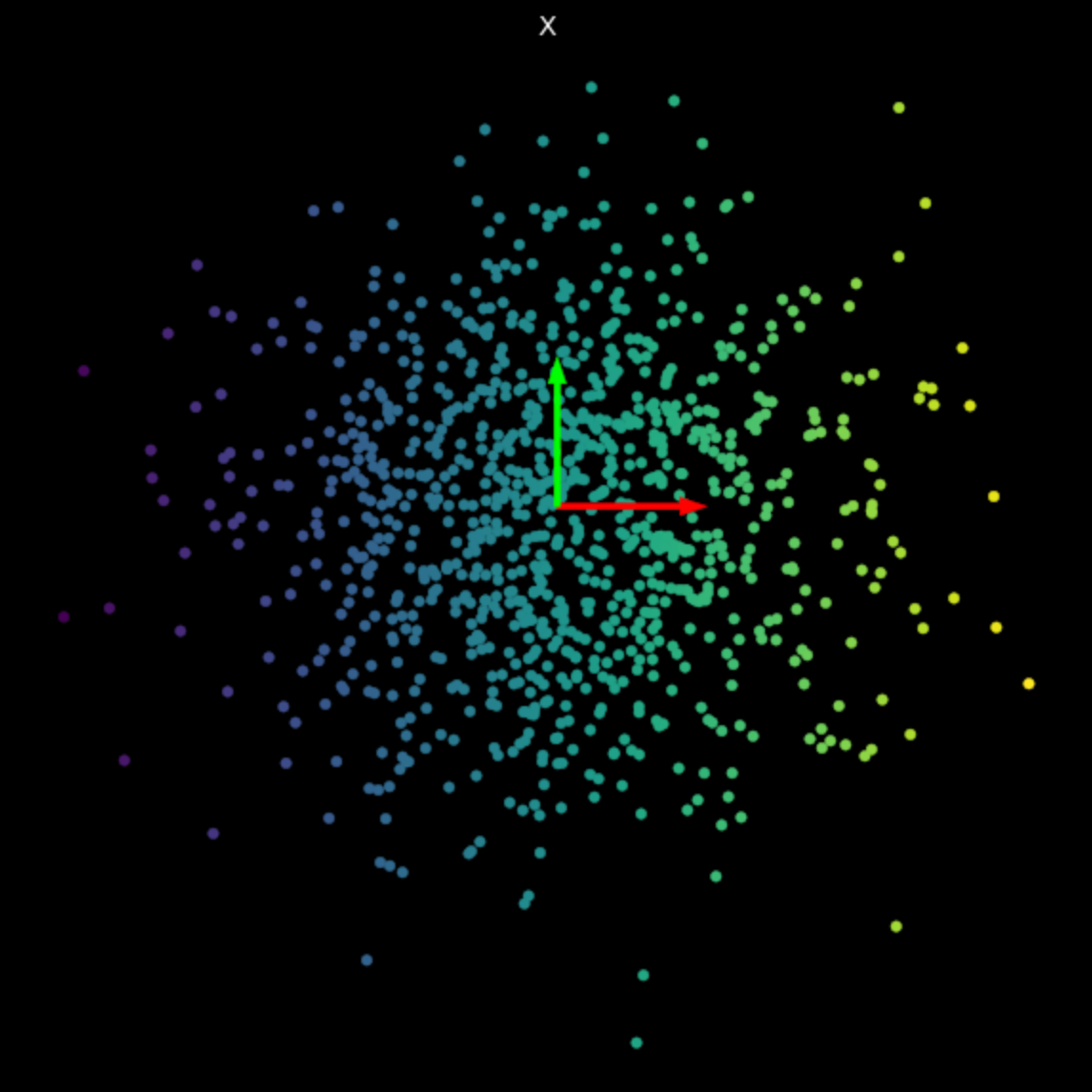
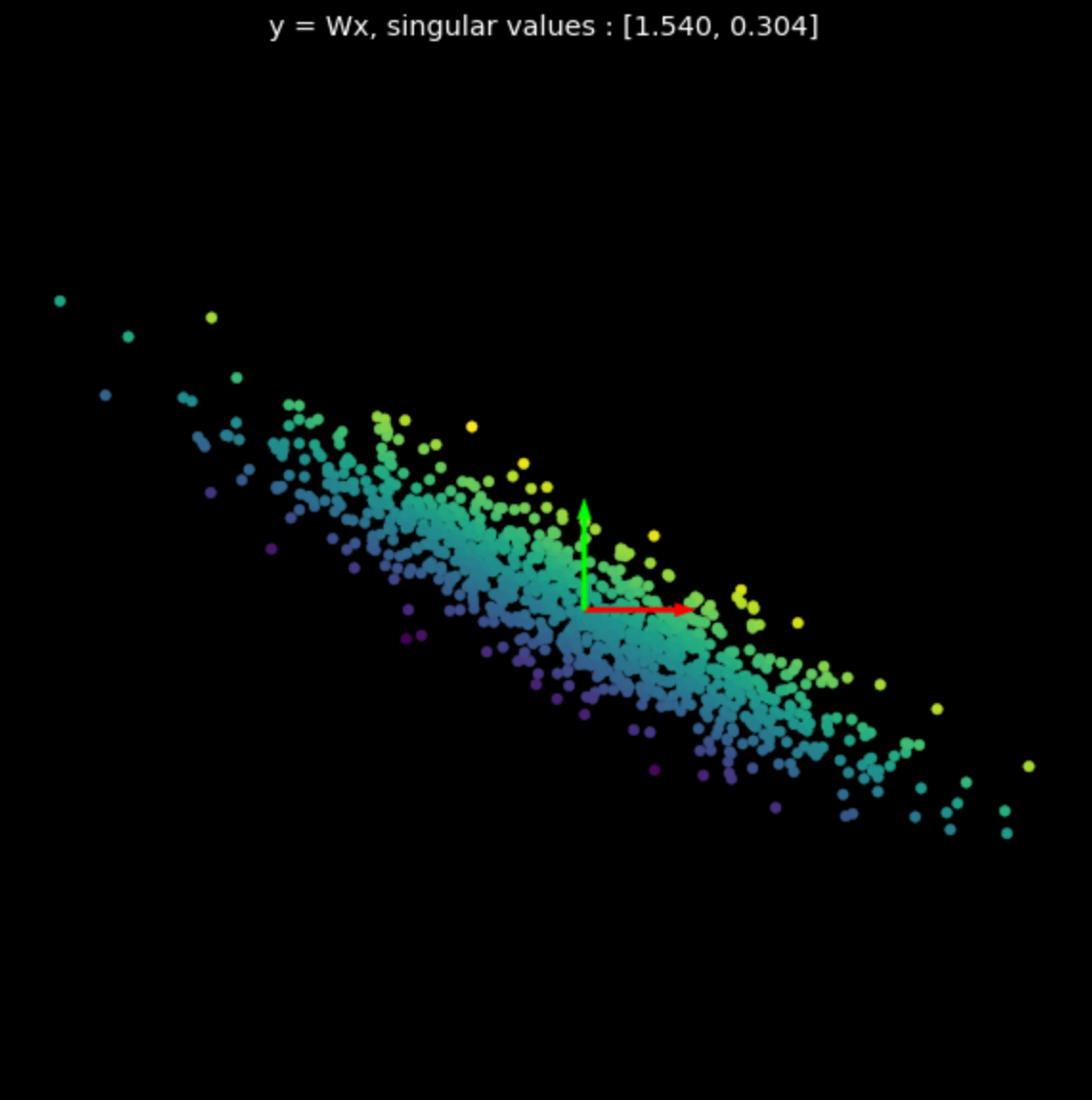
Nous visualisons les transformations linéaires de plusieurs matrices aléatoires dans la figure 3. Notez l’effet des valeurs singulières sur les transformations résultantes.

Les matrices utilisées ont été générées avec NumPy, cependant, nous pouvons également utiliser la classe nn.Linear de PyTorch avec bias = False pour créer des transformations linéaires.

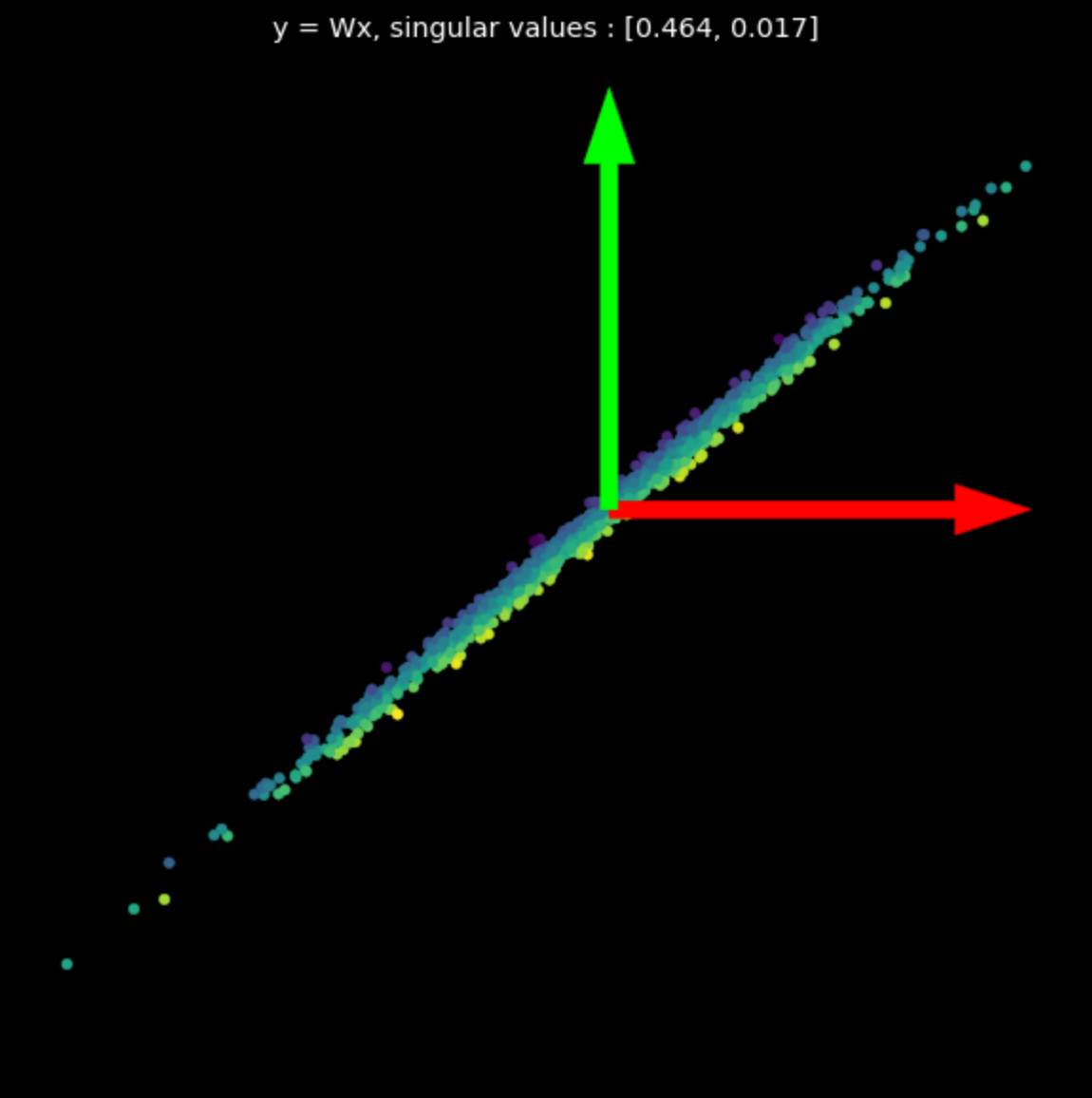(a) Points originaux	(b) $s_1$ = 1,540, $s_2$ = 0,304	(c) $s_1$ = 0,464, $s_2$ = 0,017

Transformations non linéaires

Ensuite, nous visualisons la transformation suivante :

Rappelez-vous, le graphique de $\tanh(\cdot)$ de la figure 4.

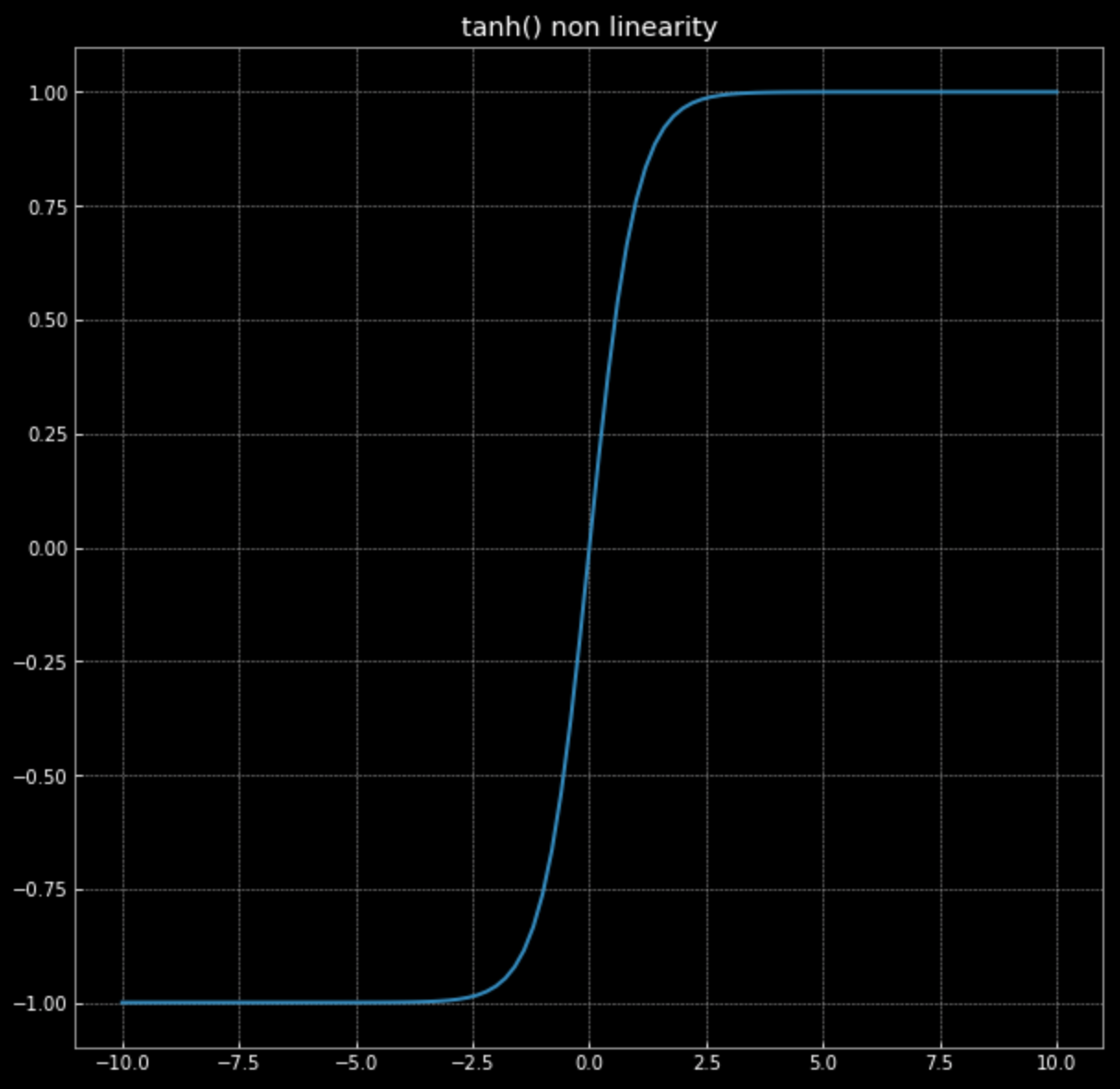
Figure 4 : Non-linéarité de la tangente hyperbolique

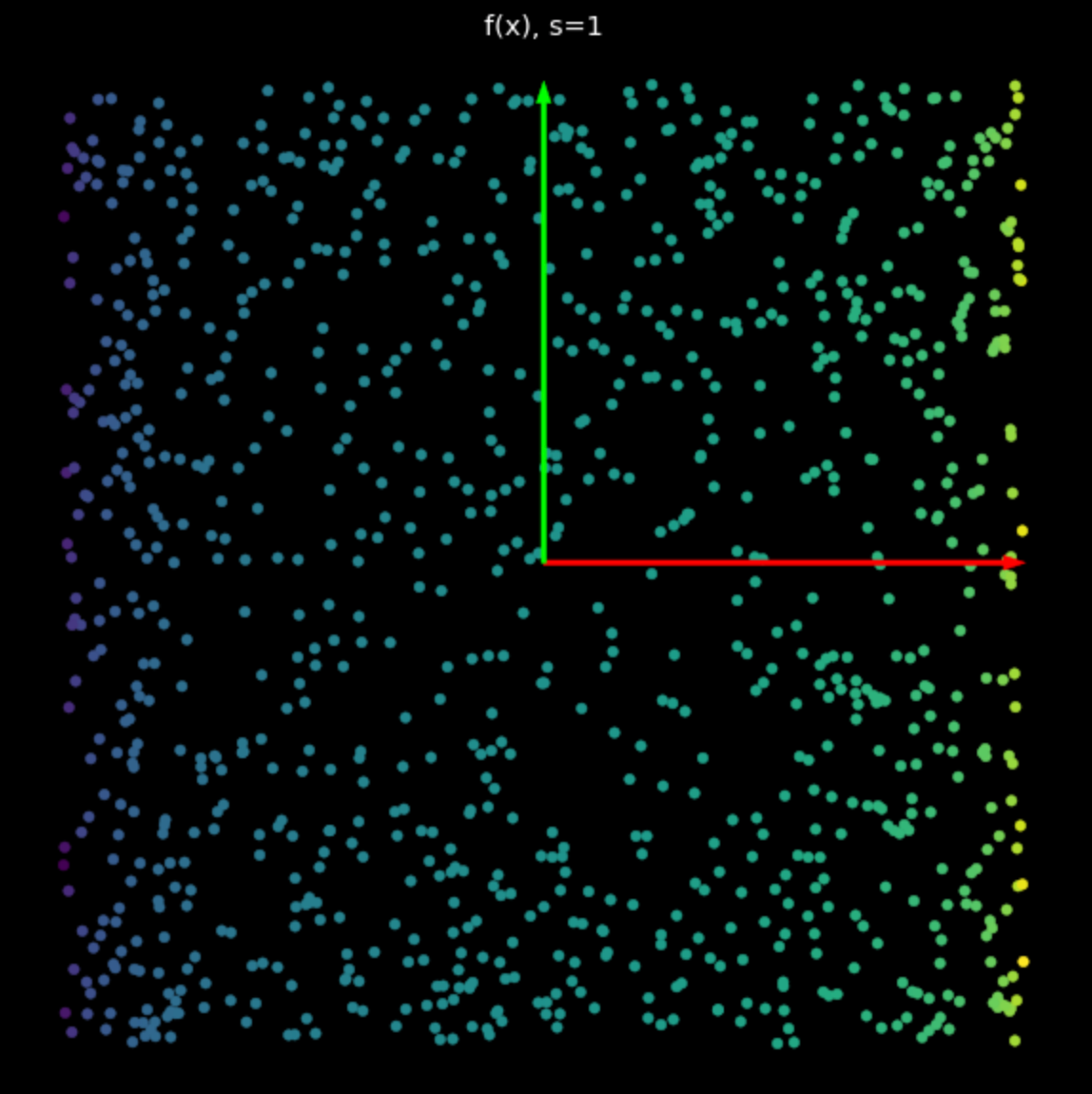
Cette non-linéarité a pour effet de délimiter des points entre $-1$ et $+1$, créant ainsi un carré. Plus la valeur de $s$ dans l’équation (2) augmente, plus les points sont poussés vers le bord du carré. C’est ce que montre la figure 5. En forçant plus de points vers le bord, nous les étalons davantage et pouvons alors tenter de les classer.

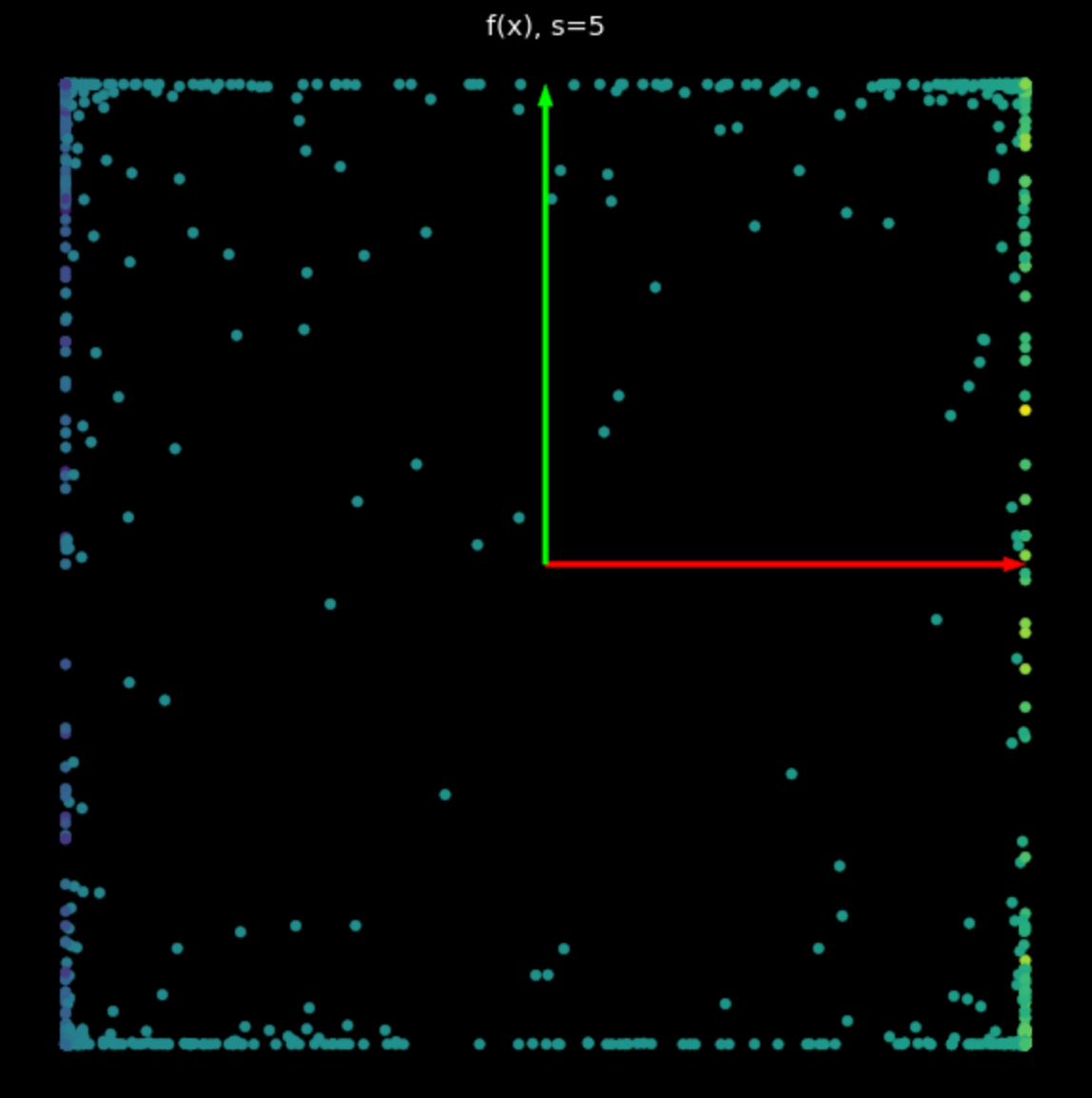(a) Non-linéarité avec $s=1$	(b) Non-linéarité avec $s=5$

Réseau neuronal aléatoire

Enfin, nous visualisons la transformation effectuée par un simple réseau de neurones non entraîné. Le réseau est constitué d’une couche linéaire, qui effectue une transformation affine, suivie d’une tangente hyperbolique non-linéaire, et enfin d’une autre couche linéaire. En examinant la transformation de la figure 6, nous constatons qu’elle est différente des transformations linéaires et non linéaires vues précédemment. Nous allons voir comment rendre utiles ces transformations effectuées par les réseaux de neurones pour notre objectif final de classification.

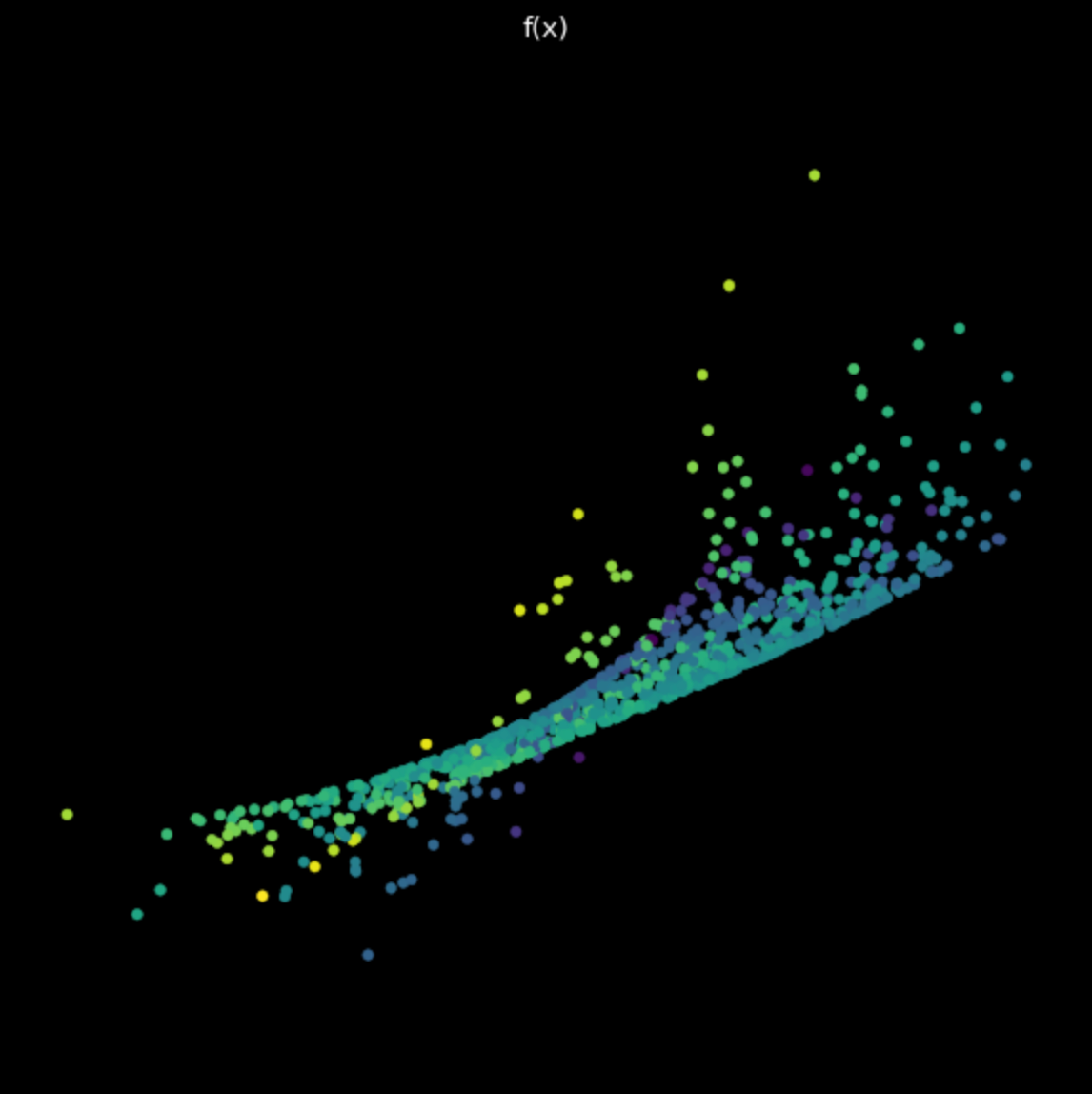
Figure 6 : Transformation d'un réseau de neurones non entraîné