에너지 기반 모델의 대조적 방법

복습하기

르쿤 박사는 처음 15분 동안 에너지 기반 모델에 대한 복습을 진행했다. 이와 관련한 정보, 특히 대조 학습 방법에 대해서는 지난주 (7주차 노트)를 다시 참조하기 바란다.

지난주 강의에서 알아보았듯, 에너지 기반 모델을 훈련시키는 방법에는 크게 두 종류가 있다:

1. 다른 부분의 에너지 값을 올리면서, $F(x_i, y’)$, 훈련 데이터 포인트의 에너지를 낮추는 대조적 방법^{Contrastive Methods}, $F(x_i, y_i)$
2. 정규화^{regularization} 방식을 이용해 낮은 에너지 영역을 최소화/제한하는 에너지 함수 $F$ 를 만드는 구조적 방법^{Architectural Methods}

각기 다른 훈련 방법의 특징을 구별하기 위해, 얀 르쿤 박사는 이전에 언급한 두 종류의 방법에 대한 7가지 훈련 전략을 추가로 요약한다. 그 중 하나는 최대 우도 방법^{Maximum Likelihood method}과 유사한 방법으로, 데이터 포인트의 에너지를 낮추고 다른 곳의 에너지를 모두 증가시키는 방법이다.

최대 우도 방법은 훈련 데이터 포인트의 에너지 값들을 확률적으로 낮추고, $y’\neq y_i$ 인 다른 모든 데이터의 에너지 값들을 낮춘다. 최대 우도는 에너지의 절대값이 아닌 오직 에너지의 차이에만 “관심”을 둔다. 확률 분포의 합은 항상 1이 되도록 정규화되기 때문에, 주어진 두 개의 데이터 포인트 사이의 비율을 비교하는 것이 단순히 각각의 절대값을 비교하는 것 보다 유용하다.

자기 지도 학습^{self-supervised learning}에서의 대조적 방법^{contrastive mothods}

대조적 방법에서는, 관측된 훈련 데이터 포인트 ($x_i$, $y_i$) 의 에너지를 낮추고, 훈련 데이터 매니폴드^manifold 외부에 존재하는 데이터 포인트들의 에너지를 높인다.

자기 지도 학습^{self-supervised learning}에서는, 입력의 한 부분을 사용해서 다른 부분을 예측한다. 우리는 이러한 모델이 지도 학습^{supervised learning}으로 훈련된 모델에 맞먹는 수준으로, 컴퓨터 비전^{computer vision}에 유용한 특징들을 생성해 낼 수 있길 바란다.

연구자들은 대조적 임베딩 방법^{contrastive embedding methods}을 자기 지도 학습에 적용하는 것이 지도 학습 모델과 필적하는 좋은 성능을 내놓을 수 있음을 경험적으로 발견했다. 아래에서 이 방법의 일부와 그 결과에 대해 살펴본다.

대조적 임베딩^{Contrastive embedding}

$x$ 가 이미지이고 $y$ 가 $x$ 의 내용(회전, 확대, 자르기, 등등.)을 유지하는 변형^{transformation}인 ($x$, $y$)쌍을 생각해보자. 우리는 이것을 positive 쌍^{양의 쌍}이라고 부른다.

그림. 1: Positive 쌍^{양의 쌍}

개념적으로, 대조적 임베딩^{contrastive embedding} 방법은 합성곱 신경망의 방식을 취하고 $x$ 와 $y$ 를 이 신경망에 입력하여 두 개의 특징 벡터^{feature vectors} $h$ 와 $h’$ 를 얻는다. $x$ 와 $y$ 는 같은 내용 (즉 positive 쌍)을 가지기 때문에, 우리는 이들의 특징 벡터가 가능한 한 비슷한 값을 가지길 바란다. 결과적으로, 우리는 $h$ 와 $h’$ 사이의 유사도를 최대화 하는 유사성 메트릭^{similarity metric} (예를 들어 코사인 유사도^{cosine similarity}) 과 손실 함수를 선택한다. 이렇게 함으로써, 우리는 훈련 데이터 매니폴드의 이미지가 갖는 에너지 값을 낮춘다.

그림. 2: Negative 쌍^{음의 쌍}

하지만, 이 매니폴드 바깥 포인트들의 에너지 또한 올려야한다. 따라서 negative 샘플, ($x_{\text{neg}}$, $y_{\text{neg}}$), 내용이 다른 이미지 (예를 들어, 다른 클래스 레이블)도 만들어낸다. 우리는 위의 네트워크에 이를 투입하고, 특징 벡터 $h$ 와 $h’$ 를 얻고, 이들 사이의 유사성을 최소화하고자 노력한다.

이 방법은 유사한 쌍들의 에너지 값을 낮추고, 유사하지 않은 쌍들의 에너지 값을 높이도록 한다.

ImageNet에 대한 최근의 결과는 이 방법이 지도학습을 통해 얻어진 특징들과 필적할 만한 수준의 객체 인식^{object recognition}에 적합한 특징들을 만들어 낼 수 있음을 보였다.

자기 지도 학습^{Self-Supervised} 결과 (MoCo, PIRL, SimCLR)

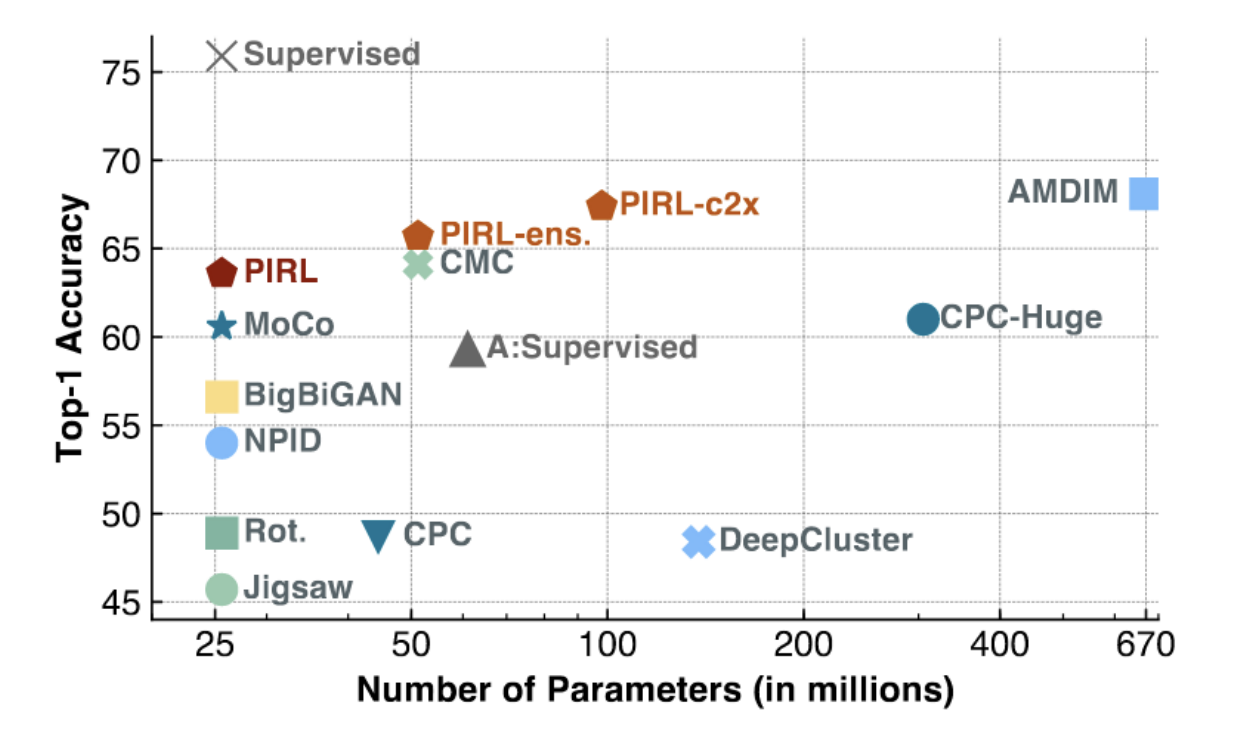
그림. 3: ImageNet에 대한 PIRL 과 MoCo

위의 그림에서 볼 수 있듯, MoCo 와 PIRL 은 (특히 적은 수의 매개 변수를 사용하는 저용량^low-capacity모델에 대해) 가장 높은 성과^{SOTA, state of the art}를 보였다. PIRL 은 지도학습 기준선 (~75%)의 top-1 선형 정확도에 접근하기 시작했다.

다음과 같은 목적함수 NCE (Noise Contrastive Estimator)를 통해 PIRL을 더 잘 이해할 수 있다.

여기에서는 두 특징 맵^maps 혹은 특징 벡터 사이의 유사성 메트릭을 코사인 유사도^{cosine similarity}로 정의한다.

PIRL이 다르게 수행하는 부분은 합성곱 특징 추출기^{convolutional feature extractor} 에서 바로 나온 직접 출력은 사용하지 않는다는 것이다. 대신에 다른 heads $f$ 와 $g$ 를 정의하는데, 이는 기본 합성곱 특징 벡터 추출기 위의 독립적인 레이어^{independent layers}로 생각할 수 있다.

종합하자면, PIRL’의 NCE 목적 함수는 다음과 같이 동작한다. 미니 배치^mini-batch에서, 하나의 positive (유사한) 쌍과, 다수의 negative (유사하지 않은) 쌍을 갖게 된다. 다음으로 변환된 이미지의 특징 벡터 ($I^t$) 와 미니 배치 안의 나머지 특징 벡터 (positive 한 개, 나머지 negative) 사이의 유사도를 계산한다. 다음 단계로 positive 쌍에서 소프트맥스 같은^softmax-like 함수로 점수^score를 계산한다. 소프트맥스 점수를 최대화 하는 것은 나머지 점수를 최소화 하는 것과 같고, 이것이 바로 우리가 에너지 기반 모델에서 원하는 것이다. 따라서 최종 손실 함수를 사용해서 유사한 쌍에서는 에너지를 낮추게 하고, 유사하지 않은 쌍에서는 에너지를 높이도록 하는 모델을 만들 수 있다.

르쿤 박사는 이 작업을 완수하기 위해서는 많은 양의 negative 샘플이 필요하다고 언급한다. SGD에서는 미니배치에서 많은 수의 negative 샘플을 일관적으로 유지하는 것이 어려울 수 있다. 따라서 PIRL은 캐시 된 메모리 뱅크^{cached memory bank}도 사용한다.

질문: 왜 L2 정규화^{L2 Norm} 대신에 코사인 유사도를 사용하는가? 답: L2 정규화를 사용하면, 두 벡터를 “짧게” (중앙에 가깝게) 만들어서 둘을 유사하게 만들거나, 또는 두 벡터를 매우 “길게” (중앙에서 멀리 떨어지게) 만들어 유사하지 않도록 만들기 매우 쉽다. 이는 L2 정규화가 단순히 벡터 간의 편미분 제곱 합이기 때문이다. 따라서 코사인 유사도를 사용하는 것은 시스템이 벡터를 짧게 또는 길게 하는 “속임수” 없이 좋은 해결 방안을 찾도록 한다.

SimCLR

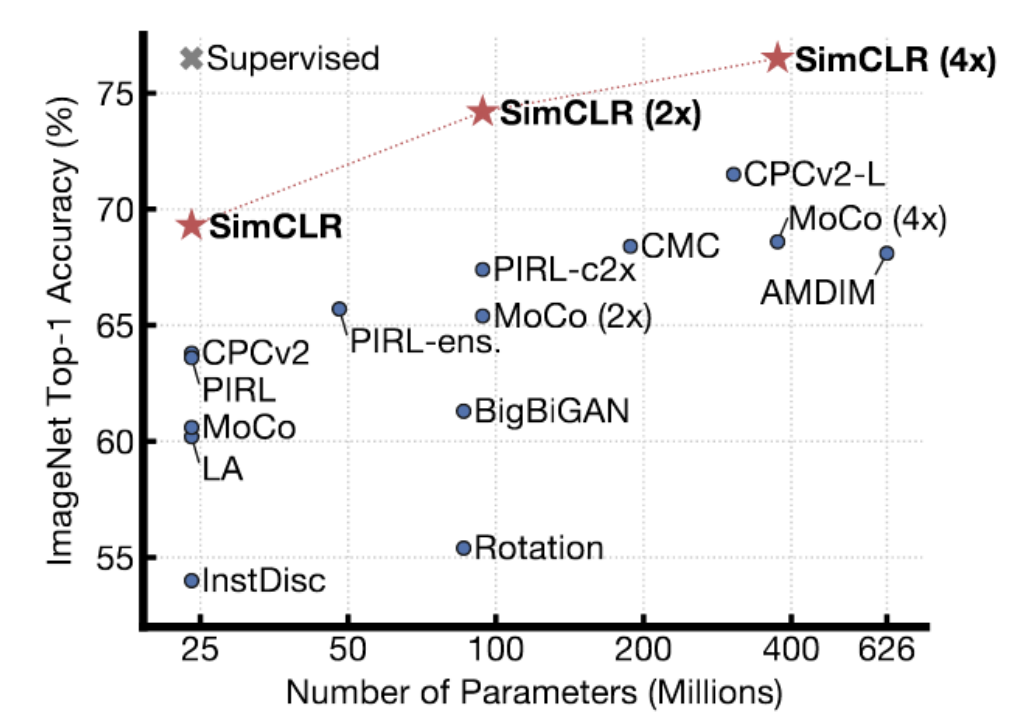
그림. 4: ImageNet에 대한 SimCLR 결과

SimCLR은 이전 방법들보다 나은 결과를 보인다. 실제로, ImageNet에 대해 top-1 선형 정확도를 보이며, ImageNet에 대해 지도학습된 모델의 성과에 도달한다. 이 기법은 정교한 데이터 확대 기법^{data augmentation method}를 이용하여 유사한 쌍을 생성하고, TPU에서 오랜 시간 동안 (굉장히 큰 배치 크기로) 학습한다. 르쿤 박사는 SimCLR이 어느 정도 대조 기법의 한계를 보여준다고 생각한다. 고차원^{hihg-dimensional} 공간에는 데이터 매니폴드보다 확실히 에너지를 높이기 위해 에너지를 끌어 올려야 하는 굉장히 많은 영역이 있다. 표현^{representation}의 차수를 늘림에 따라, 매니폴드가 아닌 영역의 에너지가 명확하게 높아지도록 더 많은 수의 negative 샘플이 필요하다.

디노이징 오토인코더^{Denoising autoencoder}

7 주차 실습 에서는 디노이징 오토인코더에 대해 논의했다. 이 모델은 손상된 입력을 원래의 입력으로 재구성해 나가면서 데이터 표현^{data representation}을 학습하는 경향을 보인다. 조금 더 구체적으로 말하자면, 손상된 데이터가 데이터 매니폴드에서 멀어짐에 따라 에너지 함수가 2차적으로^{quadratically} 증가하도록 시스템을 훈련시킨다.

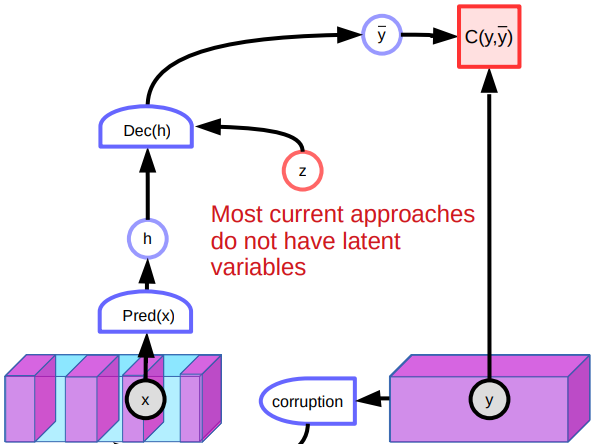
그림. 5: 디노이징 오토인코더의 구조

문제점^Issues

그러나, 디노이징 오토인코더에는 몇 가지 문제점이 있다. 한 문제점은 고차원 연속 공간^{high dimensioanl continuous space}에서 데이터 조각을 손상시키는 수 많은 방법들이 존재한다는 점이다. 이와 같은 이유로, 많은 위치에서 단순히 에너지를 높여 나가며 에너지 함수를 형성해 나갈 수 있다는 보장을 할 수 없다. 또한 이 모델은 잠재 변수를 갖지 않기 때문에 이미지 처리에 있어 성과가 낮은 것도 문제이다. 이미지를 재구성하는 데에는 다양한 방법이 있기 때문에, 시스템은 다양한 예측을 내놓고 특별히 좋은 특징을 학습하지는 않는다. 게다가, 매니폴드 중앙의 손상된 데이터 포인트들은 양쪽으로 재구성될 수 있다. 이는 에너지 함수에 편평한 지점을 만들고 전반적인 성능에 영향을 준다.

다른 대조 방법들^{Other contrastive Methods}

대조 발산^{contrastive divergence}, Ratio Matching^{비율 매칭}, Noise Contrastive Estimation^{노이즈 대조 추정}, 그리고 Minimum Probability Flow^{최소 확률 흐름} 과 같은 다른 대조 방법들이 존재한다. 대조 발산의 기본 개념에 대해 간단히 논의해 본다.

대조 발산

대조 발산(CD, Contrastive Divergence)은 입력 샘플을 똑똑하게 손상시켜서 데이터 표현을 학습하는 또 다른 모델이다. 연속 공간에서, 먼저 훈련 샘플 $y$를 고르고 이것의 에너지를 낮춘다. 이 샘플에 대해서 우리는 일종의 그래디언트에 기반한 과정^{gradient-based process}을 사용해서 노이즈가 있는 에너지 표면에서 아래로 이동한다. 만일 입력 공간이 이산적이라면, 에너지를 수정하기 위해 훈련 샘플을 무작위로 교란시킬 수 있다. 만일 얻어진 에너지 값이 낮으면 가지고 있는다. 에너지 값이 낮지 않다면, 어떤 확률값에 따라 그것을 버린다. 이러한 과정을 계속하면 결국 $y$의 에너지 값이 낮아진다. 이 다음, $y$와 이것의 대조 샘플 $\bar y$의 손실함수 값을 비교하여 매개 변수를 업데이트 할 수 있다.

Persistent Contrastive Divergence^{지속적 대조 발산}

대조 발산의 개선된 모델 중 하나는 persistent contrastive divergence이다. 이 시스템은 많은 “입자^particles“를 사용하고 그 위치를 기억한다. 이 입자들은 기존의 대조 발산^{CD, Contrastive Divergence}에서 그랬던 것 처럼 에너지 표면에서 아래로 이동한다. 결국, 이 입자들은 에너지 표면 상에서 낮은 에너지들의 위치를 파악하고 이들의 에너지를 높일 것이다. 그러나 이 시스템은 차원의 확장에 따른 스케일 조절이 잘 되지 않는다.