Méthodes d'enchâssements joints contrastives

Apprentissage de représentations visuelles

L’apprentissage de représentation consiste à entraîner un système à produire des représentations, pour la détection de caractéristiques ou pour la classification, à partir de données brutes. L’apprentissage de représentations visuelles concerne les représentations d’images ou de vidéos en particulier.

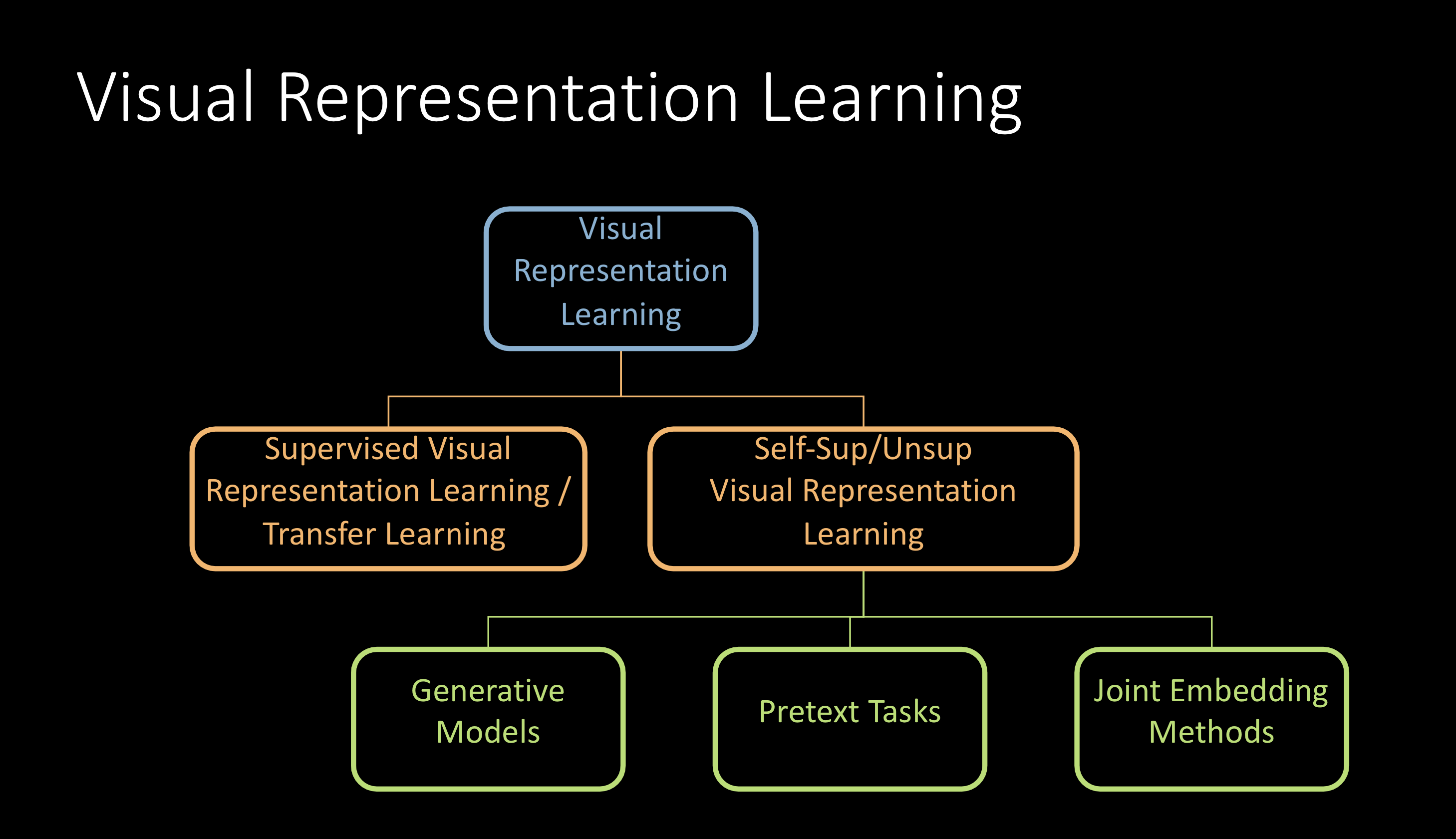
Figure 1 : Apprentissage de représentations visuelles

On peut les classer comme indiqué ci-dessus et ce qui suit portera essentiellement sur l’apprentissage autosupervisé de représentation visuelle.

Apprentissage autosupervisé de représentations visuelles

Il s’agit d’un processus en deux étapes comprenant un pré-entraînement et une évaluation.

Etape 1 : pré-entraînement

Utilisation d’une grande quantité de données non étiquetées pour entraîner un réseau backbone. Différentes méthodes produiront le backbone différemment.

Etape 2 : évaluation

Elle peut être réalisée de deux manières : l’extraction de caractéristiques et le finetuning. Ces deux méthodes génèrent une représentation à partir de l’image et l’utilisent ensuite pour entraîner la tête de tâche en aval (DsTH pour Downstream Task Head). L’apprentissage de la tâche en aval se fait donc dans l’espace de représentation au lieu de l’espace d’image. La seule différence entre ces deux méthodes est l’arrêt du gradient avant l’encodeur. Dans le finetuning, nous pouvons changer l’encodeur, contrairement à l’extraction de caractéristiques.

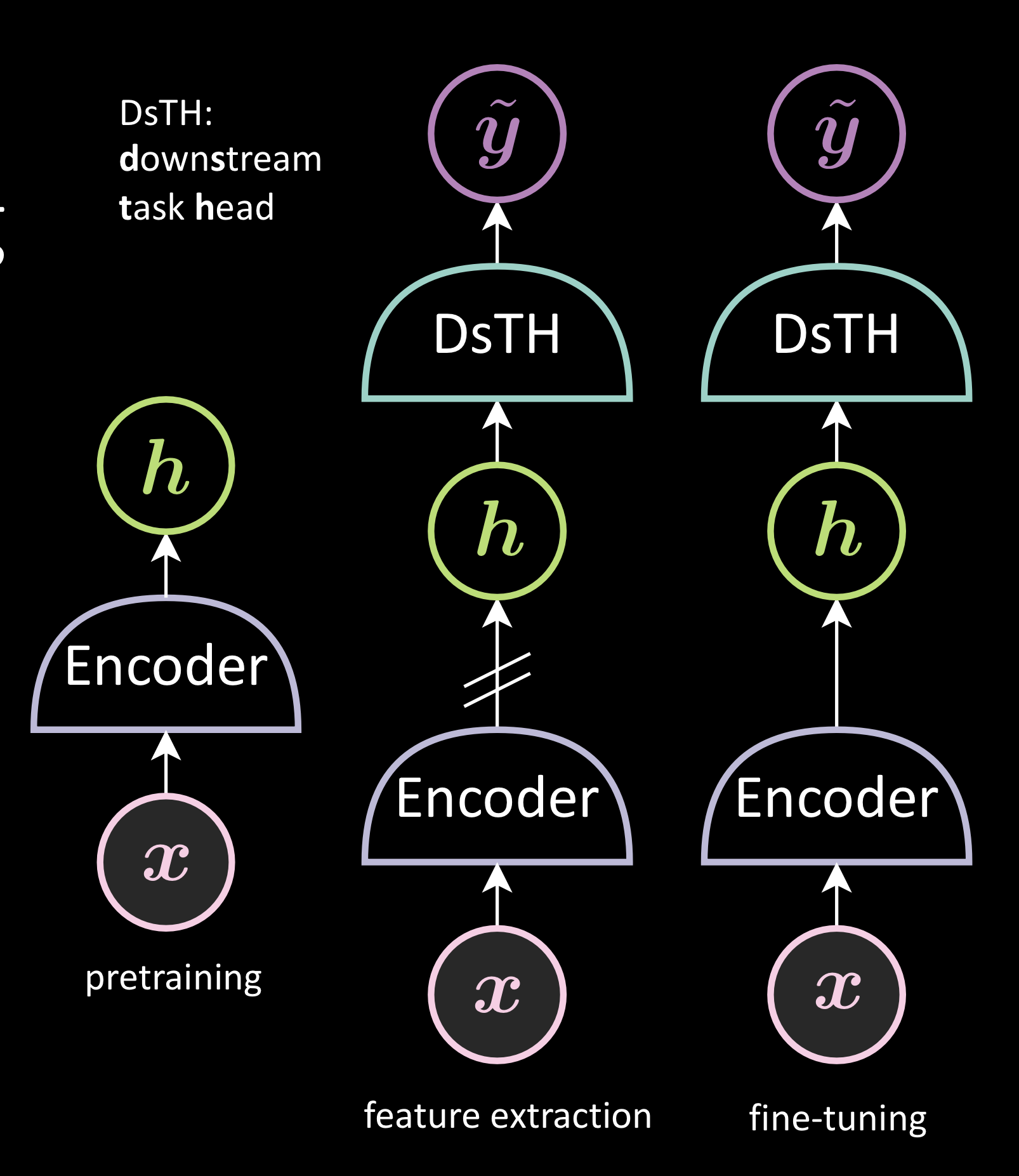
Figure 2 : Apprentissage autosupervisé de représentations visuelles

Modèles génératifs

Le plus Populaire est l’auto-encodeur débruiteur. On entraîne le modèle à reconstruire l’image originale à partir de l’image bruitée. Après l’entraînement, on réentraîne l’encodeur pour la tâche en aval.

Problèmes

Le modèle tente de résoudre un problème qui est trop difficile. Par exemple, pour beaucoup de tâches en aval, il ne faut pas reconstruire l’image qui est un problème plus complexe que la tâche en aval elle-même. De même, il arrive que la fonction de perte ne soit pas assez bonne. Par exemple, la distance euclidienne utilisée comme métrique de perte de reconstruction n’est pas une bonne métrique pour comparer la similarité entre deux images.

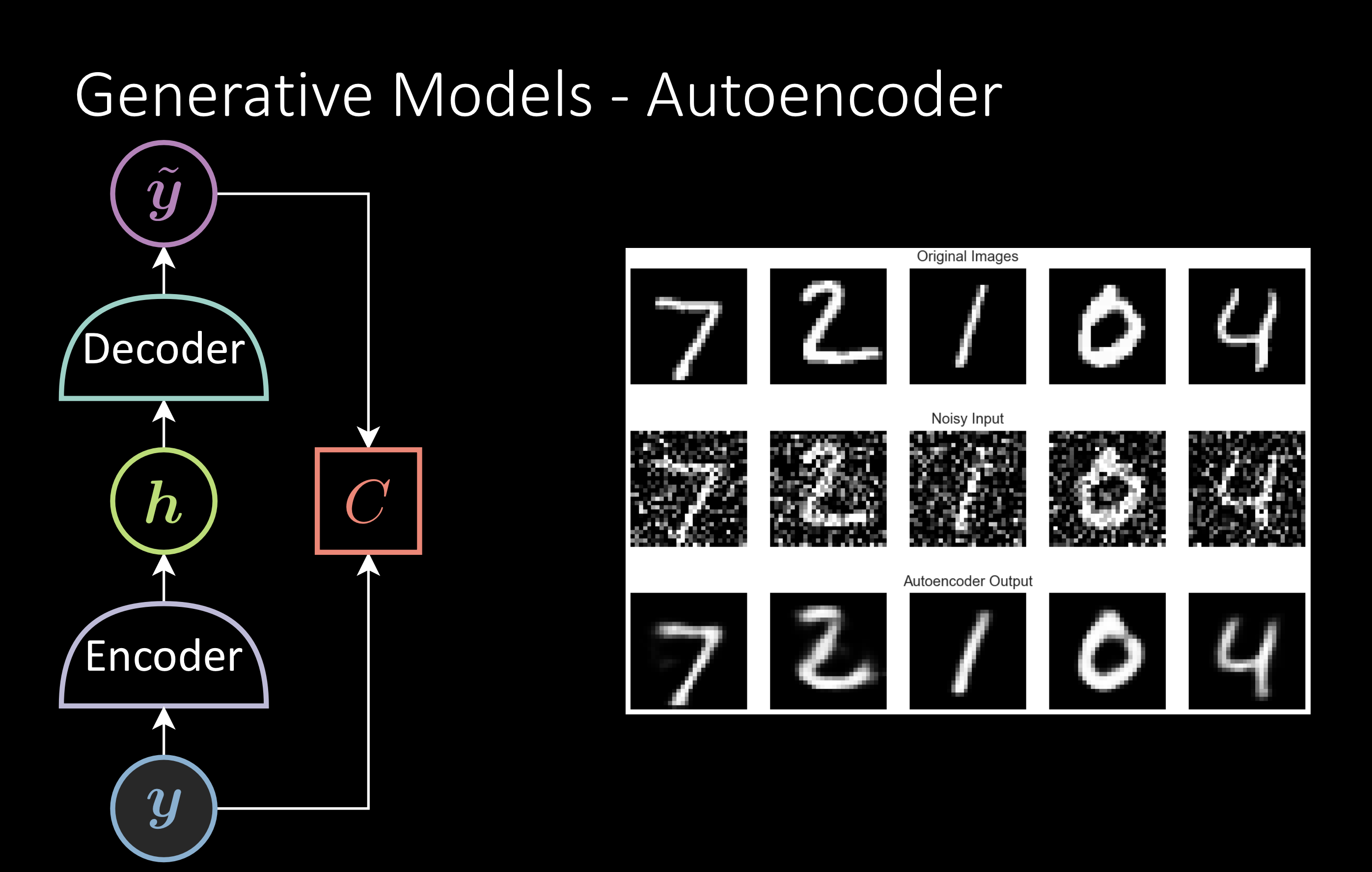
Figure 3 : Modèles génératifs, l’auto-encodeur

Tâches de prétexte

C’est presque la même chose que ci-dessus mais on entraîne le modèle à trouver un moyen intelligent de générer des pseudo-étiquettes. Par exemple, étant donné l’image d’un tigre, l’image mélangée est l’entrée x et la sortie y serait la bonne manière d’étiqueter les patchs. Le fait que le réseau réussisse à réinventer les patchs indique qu’il comprend l’image.

Problèmes

La conception de la tâche de prétexte est délicate. Si vous la concevez trop facile, le réseau n’apprendra pas une bonne représentation. Mais si vous la concevez trop difficile, elle peut devenir plus difficile que la tâche en aval et le réseau ne sera pas bien entraîné. En outre, les représentations générées par cette méthode seront adaptées à la tâche spécifique en aval.

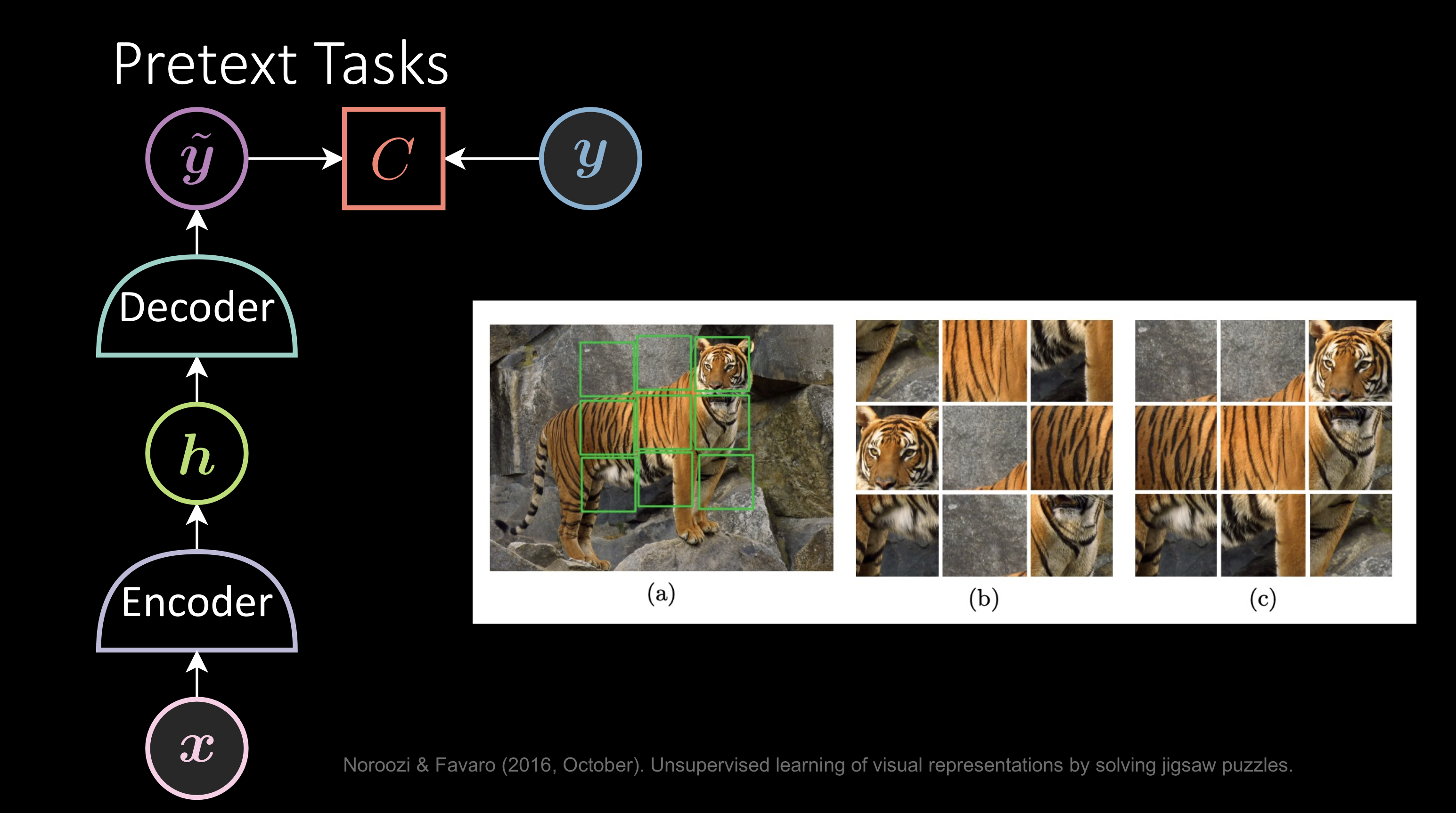
Figure 4 : Tâches de prétexte

Les méthodes d’enchâssements joints

Les méthodes d’enchâssements joints tentent de rendre leur backbone robuste à certaines distorsions et invariant à l’augmentation des données.

Par exemple, comme le montre l’image ci-dessous, pour l’image d’un chien, vous prenez deux versions déformées de l’image, puis vous les passez dans les backbones pour générer des représentations et vous faites en sorte qu’elles soient proches les unes des autres. Ainsi, vous vous assurez que les deux images partagent certaines informations sémantiques.

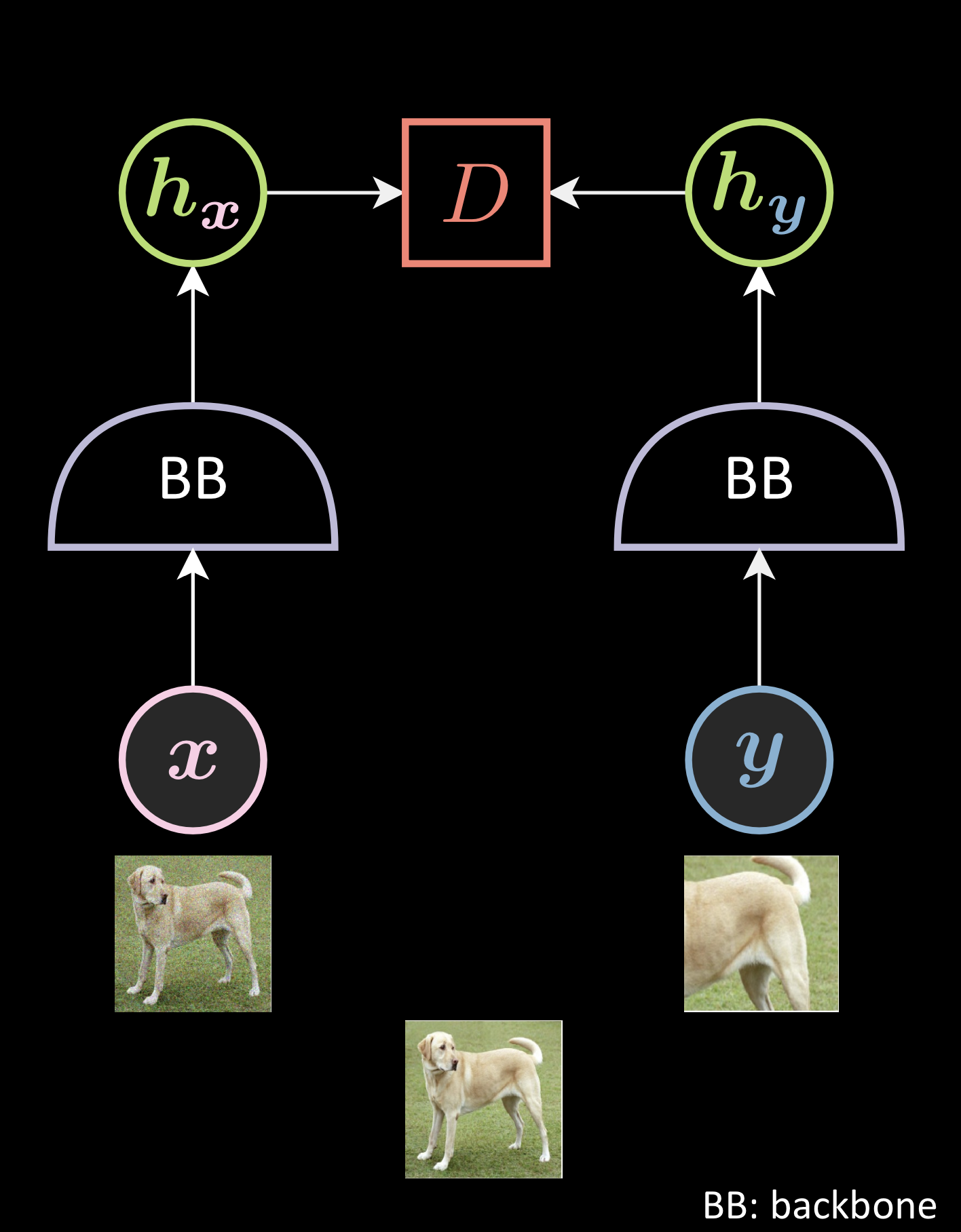
Figure 5 : Augmentation de données en JEM

Le réseau pourrait s’effondrer avec la seule condition ci-dessus car il peut devenir invariant non seulement aux distorsions mais aussi à l’entrée dans son ensemble, c’est-à-dire que, quelle que soit l’entrée, il pourrait générer la même sortie. Les JEMs essaient d’empêcher cette solution triviale de différentes manières.

Au lieu de considérer uniquement l’énergie locale (entre deux paires d’images déformées), ces méthodes ont un batch d’images et s’assurent que la collection de la représentation, $\green{H}_{\vx}$, n’a pas les mêmes lignes ou colonnes (ce qui correspond à la solution triviale).

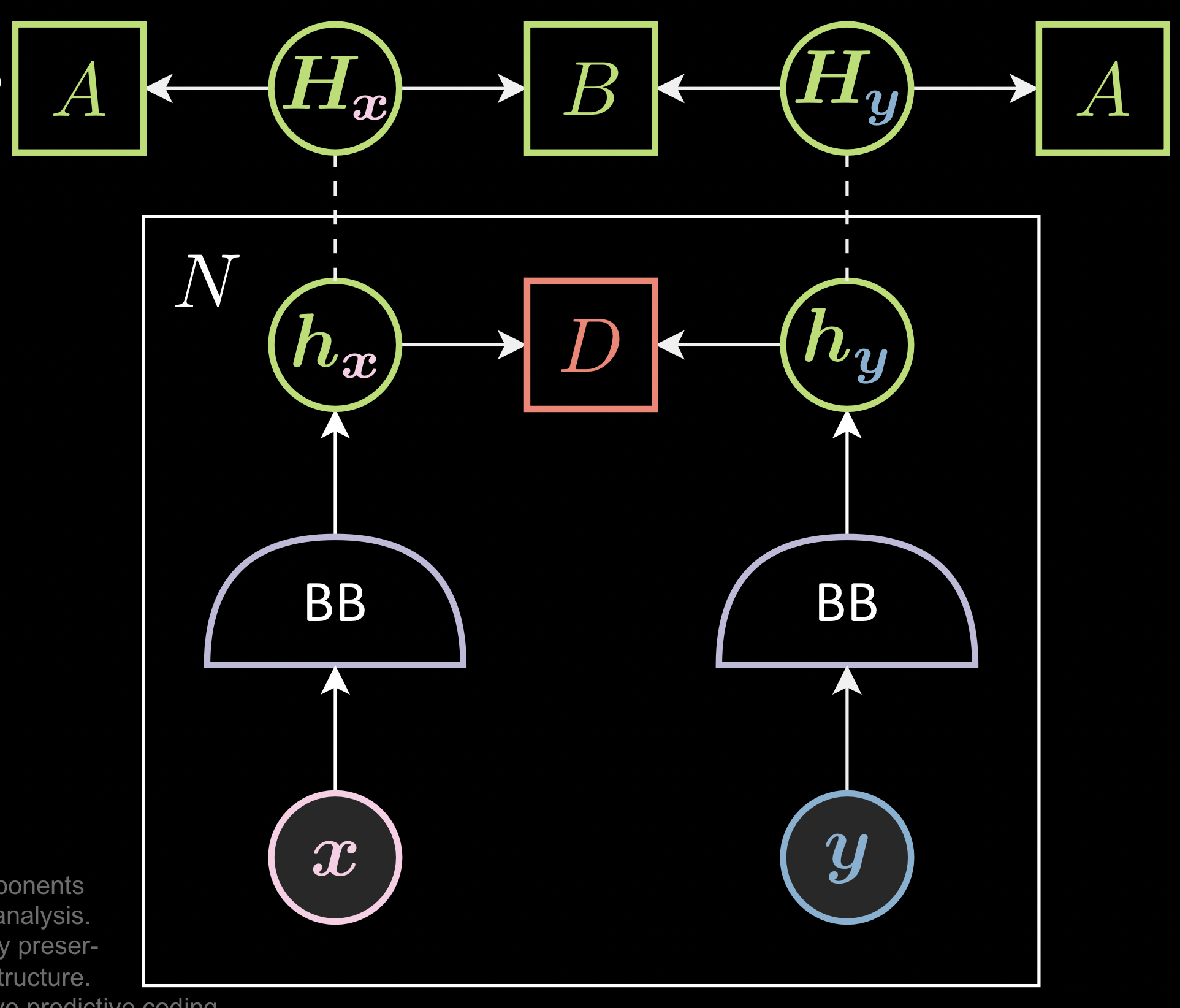
Figure 6 : Empêcher les solutions triviales dans les JEMs

D est l’énergie qui est calculée par échantillon. A et B sont les fonctions de perte qui sont calculées pour les batchs de taille N. L’opérateur en pointillé est pour l’empilement. $h_x$, $h_y$ sont les représentations de $x$, $y$ et $H_x$ et $H_y$ sont les matrices avec chaque ligne de $h_x$ et $h_y$.

Composants :

Chaque méthode d’enchâssements joints a les composantes suivantes :

1. Augmentation des données ($\vx$ et $\vy$) : la façon dont vous générez les deux versions déformées de l’image.
2. Le backbone ($\lavender{BB}$) : la définition du backbone.
3. La fonction d’énergie ($\red{D}$) : la définition de la distance entre les deux représentations.
4. Les fonctions de perte ($\green{A}$ et $\green{B}$) : la définition des fonctions de perte calculées par batch de taille N.

Fonctions de perte des méthodes d’enchâssements joints :

Les fonctions de perte des méthodes d’enchâssements joints contiennent deux composantes :

1. Un terme qui rapproche la paire positive
2. Un terme (implicite) qui empêche la solution triviale (sortie constante). Le terme est implicite car beaucoup d’« autres méthodes » n’ont pas de terme explicite pour empêcher la solution triviale.

Pour rendre l’entraînement stable, les gens normalisent généralement les enchâssements ou mettent un seuil sur la fonction de perte pour empêcher la norme des enchâssements de devenir trop grande ou trop petite.

Méthodes d’entraînement

Les méthodes d’entraînement peuvent être classées en quatre types différents :

1. Les méthodes contrastives
2. Les méthodes non-contrastives
3. Les méthodes de regroupement (clustering)
4. Les « autres méthodes »

Méthodes contrastives

Les méthodes contrastives rapprochent les paires positives et éloignent les paires négatives. Plus de détails sur les méthodes contrastives, y compris MoCo, PIRL et SimCLR, sont disponibles dans l’édition 2020 du cours.

La fonction de perte InfoNCE :

SimCLR et MoCo utilisent tous deux la fonction de perte InfoNCE.

Le premier terme indique la similarité entre les paires positives. Le second terme est la fonction softmax entre toutes les paires négatives. Nous voulons minimiser cette fonction entière.

Remarquons qu’elle donne des poids différents aux différents échantillons négatifs. La paire négative qui a une forte similarité est poussée beaucoup plus fort que la paire négative avec une faible similarité parce qu’il y a la softmax. De plus, la mesure de similarité est ici le produit scalaire hermitien entre les deux représentations que l’on normalise pour éviter l’explosion du gradient. Ainsi, même si le vecteur est devenu long, le terme garantit qu’il s’agit d’un vecteur unitaire.

Banque mémoire

Comme déjà mentionné, ces modèles nécessitent des échantillons négatifs. Cependant, trouver des paires négatives devient difficile lorsque les espaces d’enchâssements deviennent grands.

Pour résoudre ce problème, SimCLR et MoCo utilisent des batchs de grande taille pour trouver les échantillons. La différence entre SimCLR et MoCo est la façon dont ils traitent la grande taille des batchs. SimCLR utilise une taille de batchs de 8192. Cependant, MoCo essaie de résoudre l’exigence d’une grande taille de batch sans en utiliser réellement une grâce à une banque mémoire. Au lieu d’utiliser des échantillons négatifs provenant uniquement du batch actuel, on en collecte dans les batchs précédents. Par exemple : pour un batch de taille 256, l’agrégation des 32 batchs précédents d’échantillons négatifs donne une taille de 8192. Cette méthode permet d’économiser de la mémoire et évite d’avoir à générer les échantillons négatifs encore et encore.

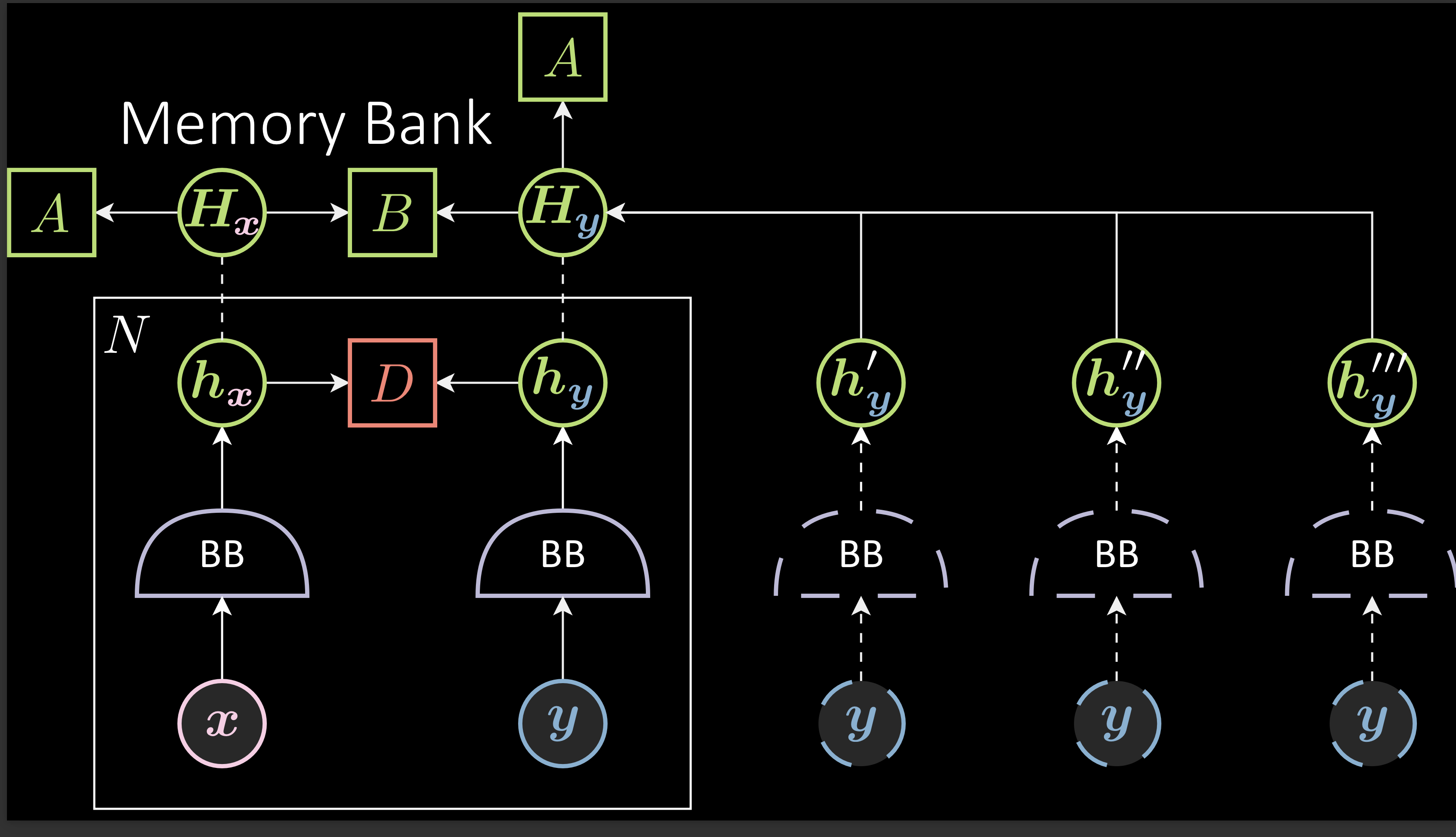
Figure 7 : Banque mémoire

Problème : Parce que B est mis à jour à chaque pas de temps, le backbone est mis à jour à chaque pas de temps, alors après un certain temps, les vieux échantillons négatifs ne sont plus encore valides ce qui peut mener à une baisse des performances. Pour éviter cela, MoCo utilise un backbone avec momentum qui ralentit l’entraînement du backbone de droite. Dans ce cas, la différence entre le vieux backbone avec momentum et le nouveau backbone avec momentum n’est pas grande, conservant la validité des échantillons négatifs même après un certain temps.

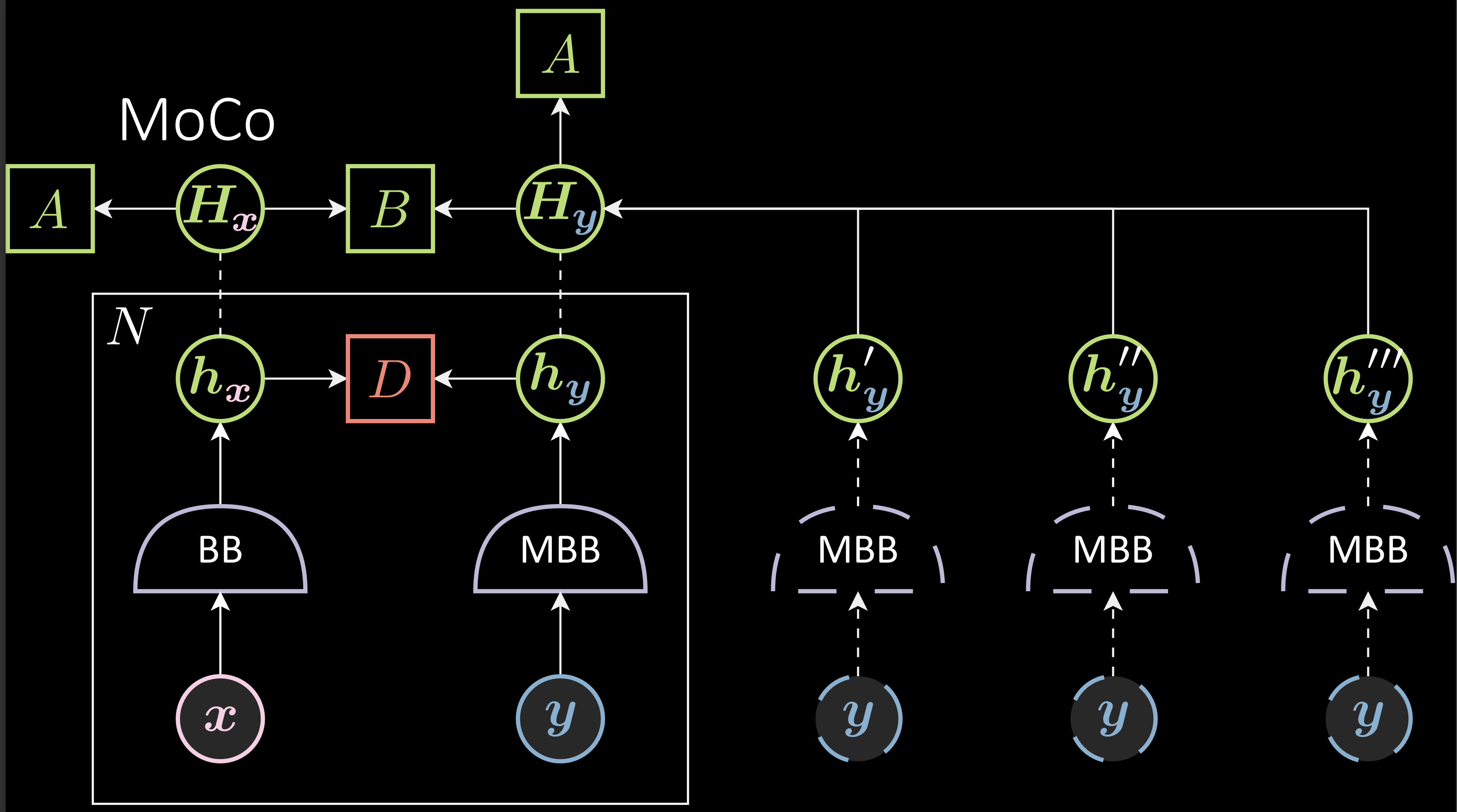
Figure 8 : Banque mémoire avec backbone avec momentum

$\vartheta_{t+1}$ (paramètres du backbone avec momentum) est l’exponentielle de la moyenne mobile de $\theta_{t}$. Le taux d’apprentissage de $\vartheta$ est $(1 - m)* \eta$. Une grande valeur de $m$ rend $\vartheta_{t}$ stable. $m$ = 1 rend $\vartheta_{t}$ non entraîné. Si $m$ = 0, $\vartheta_{t+1}$ = $\theta_{t+1}$.

Désavantages des méthodes contrastifs

En pratique, les méthodes contrastives nécessitent une énorme configuration pour fonctionner. Elles requièrent des techniques comme le partage de poids entre les branches, de la normalisation par batch, normalisation par caractéristiques, quantification de sortie, arrêt du gradient, banque mémoire, etc. Ces méthodes sont difficiles à analyser et sont instables sans toutes ces techniques.