Commande à modèle prédictif (version EBM)

Plan d’action

• Commande à modèle prédictif [Nous sommes ici dans cette section].
  • Rétropropagation par l’équation cinématique
  • Minimisation de la latence
• Truck backer-upper
  • Apprentissage d’un émulateur de la cinématique à partir d’observations
  • Entraînement d’une politique
• Prédiction ét apprentissage d’une politique sous incertitude (PPUU de l’anglais « Prediction and Policy learning Under Uncertainty »)
  • Environnement stochastique
  • Minimisation des incertitudes
  • Découplage latent

Equations de transition d’état - Evolution de l’état

Nous abordons ici une équation de transition d’état où $\vx$ représente l’état et $\vu$ représente la commande. Nous pouvons formuler la fonction de transition d’état dans un système à temps continu où $\vx(t)$ est une fonction de la variable continue $t$.

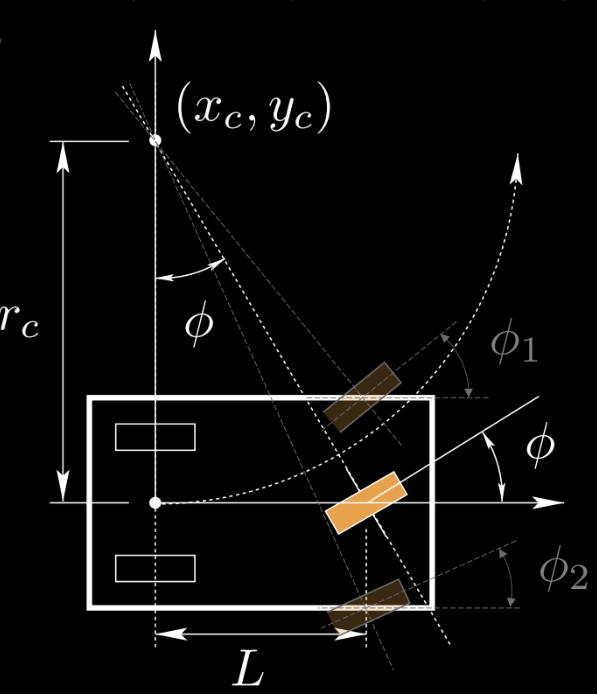
Figure 1 : Illustration de l'état et de la commande d'un tricycle

Nous utilisons un tricycle comme exemple pour l’étudier. La roue orange est la commande $\vu$, $(x_c,y_c)$ est le centre de rotation instantané. On peut aussi avoir deux roues à l’avant. Pour simplifier, nous utilisons une roue comme exemple.

Dans cet exemple, $\vx=(x,y,\theta,s)$ est l’état, $\vu=(\phi,\alpha)$ est la commande.

Nous pouvons reformuler l’équation différentielle du système à temps continu en système à temps discret :

Pour être clair, nous montrons les unités de $\vx, \vu$.

Jetons un coup d’oeil à différents exemples. Nous utilisons une couleur différente pour les variables qui nous intéressent.

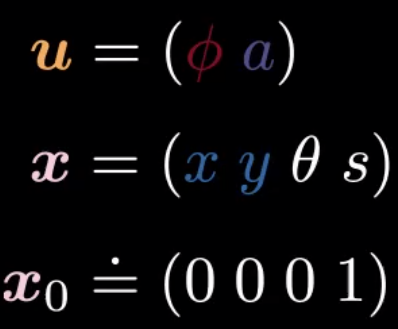
Figure 2 : Formulation de l'état

Exemple 1 : Mouvement linéaire uniforme : pas d’accélération, pas de direction.

Figure 3 : Contrôle d'un mouvement linéaire uniforme

Figure 4 : Etat d'un mouvement linéaire uniforme

Exemple 2 : Ecrasement sur lui-même : accélération négative, pas de direction.

Figure 5 : Contrôle de l'incurvation sur elle-même

Figure 6 : État de l'incurvation sur elle-même

Exemple 3 : Onde sinusoïdale : direction positive pour la première partie, direction négative pour la deuxième partie.

Figure 7 : Contrôle de l'onde sinusoïdale

Figure 8 : Etat de l'onde sinusoïdale

Algorithme de Kelley-Bryson

Que faire si l’on veut que le tricycle atteigne une destination donnée à une vitesse donnée ?
Cela peut être réalisé par inférence à l’aide de l’algorithme de Kelley-Bryson, qui utilise la rétropropation à travers le temps et la descente de gradient.

Récapitulation des réseaux de neurones récurrents (RNNs)

Nous pouvons comparer le processus d’inférence ici avec le processus d’entraînements des RNNs.

Voici le schéma d’un RNN. Nous introduisons la variable $\vx[t]$ et l’état précédent $\vh[t-1]$ dans le prédicteur, tandis que $\vh[0]$ est fixé à zéro. Le prédicteur sort la représentation cachée $\vh[t]$.

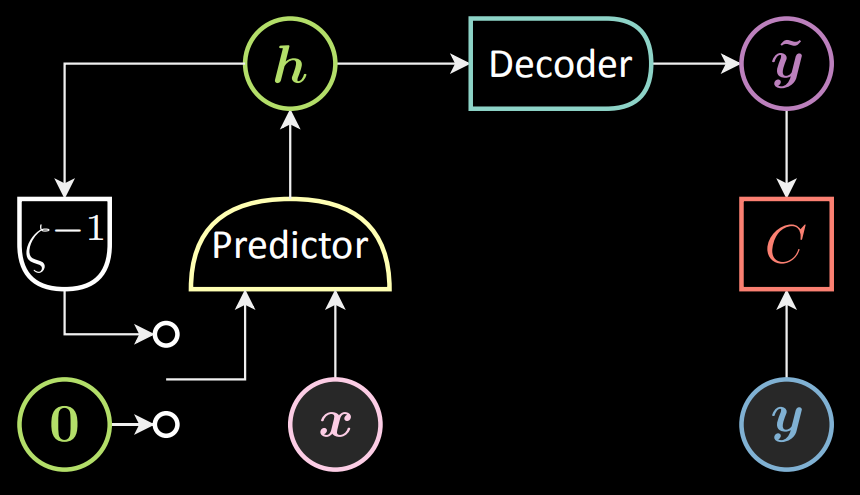
Figure 9 : Schéma d'un RNN

Contrôle optimal (inférence)

Dans le contrôle optimal (inférence) présenté ci-dessous, nous introduisons la variable latente (contrôle) $\vz[t]$ et l’état précédent $\vx[t-1]$ dans le prédicteur, tandis que $\vx[0]$ est fixé à $\vx_0$. Le prédicteur sort l’état $\vx[t]$.

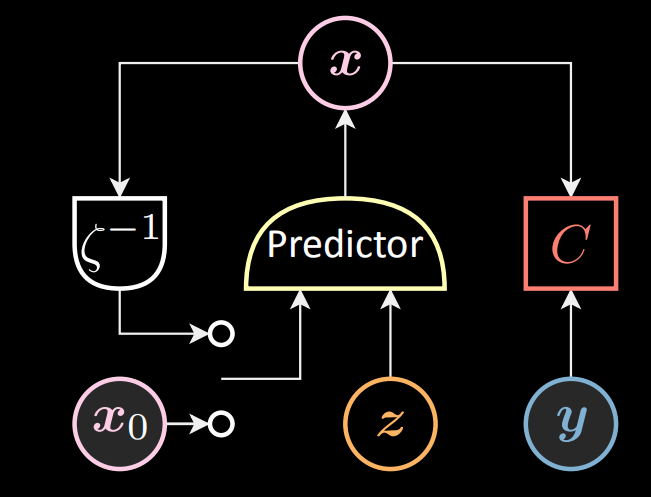
Figure 10 : Schéma de la commande optimale

La rétropropagation est implémentée à la fois dans le RNN et dans le contrôle optimal. Cependant, la descente de gradient est implémentée par rapport aux paramètres du prédicteur dans le RNN et est implémentée par rapport à la variable latente $\vz$ dans le contrôle optimal.

Version dépliée du contrôle optimal

Dans la version dépliée du contrôle optimal, le coût peut être fixé soit à l’étape finale du tricycle, soit à chaque étape du tricycle. En outre, les fonctions de coût peuvent prendre de nombreuses formes, telles que la distance moyenne, la softmin, etc.

Fixer le coût à l’étape finale

Sur la figure ci-dessous, nous pouvons voir qu’il n’y a qu’un seul coût $c$ fixé à l’étape finale (étape 5) mesurant la distance de notre cible $\vy$ et de l’état $\vx[5]$ avec le contrôle $\vz[5]$.

Figure 11 : Coût de l'étape finale

$(1)$ Si la fonction de coût ne fait intervenir que la position finale sans restriction sur la vitesse finale, nous pouvons obtenir les résultats après inférence présentés comme ci-dessous.

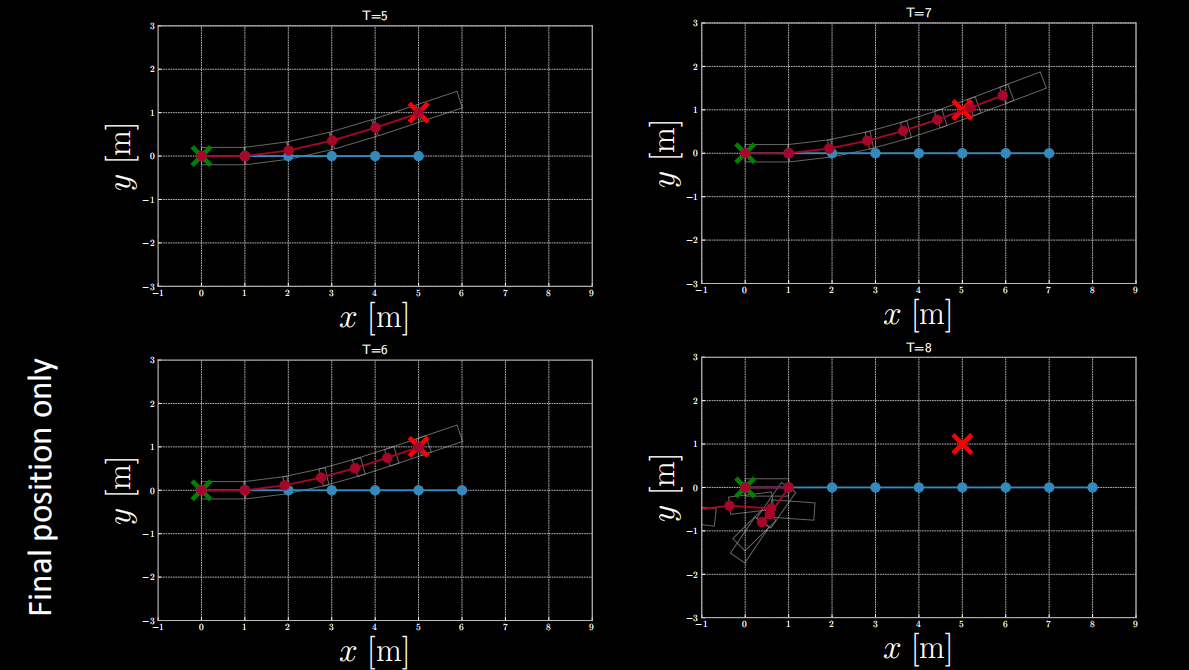
Figure 12 : Fonction de coût faisant intervenir uniquement la position finale.

D’après la figure ci-dessus, on constate que lorsque $T=5$ ou $T=6$, la position finale respecte la position cible. Mais lorsque $T$ est supérieur à 6, la position finale ne le fait pas.

$(2)$ Si la fonction de coût fait intervenir la position finale et la vitesse finale nulle, on peut obtenir les résultats après inférence présentés ci-dessous.

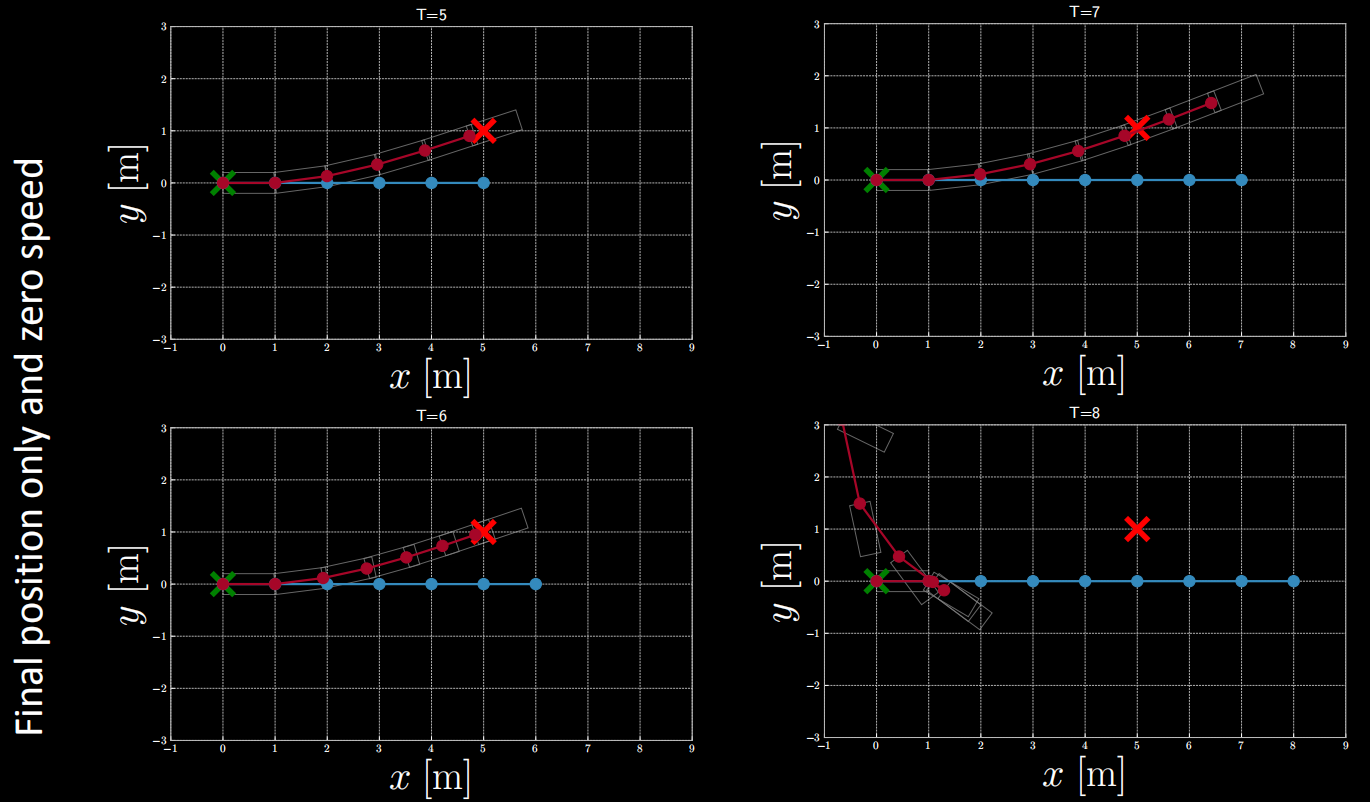
Figure 13 : Fonction de coût faisant intervenir la position finale et la vitesse finale nulle.

D’après la figure ci-dessus, on constate que lorsque $T=5$ ou $T=6$, la position finale correspond à peu près à la position cible. Mais que lorsque $T$ est supérieur à 6, la position finale ne correspond pas.

Définir le coût à chaque étape

D’après la figure ci-dessous, nous pouvons voir qu’il y a un coût $c$ fixé à chaque étape.

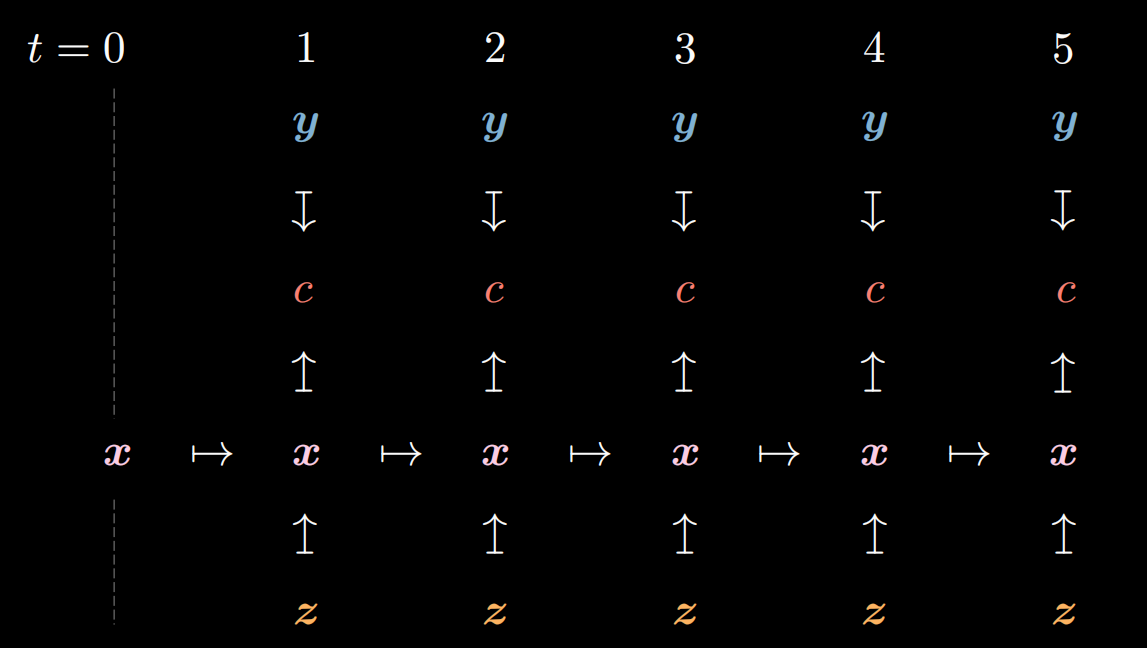
Figure 14 : Coût de chaque étape

Exemple de coût $(1)$ : Distance moyenne

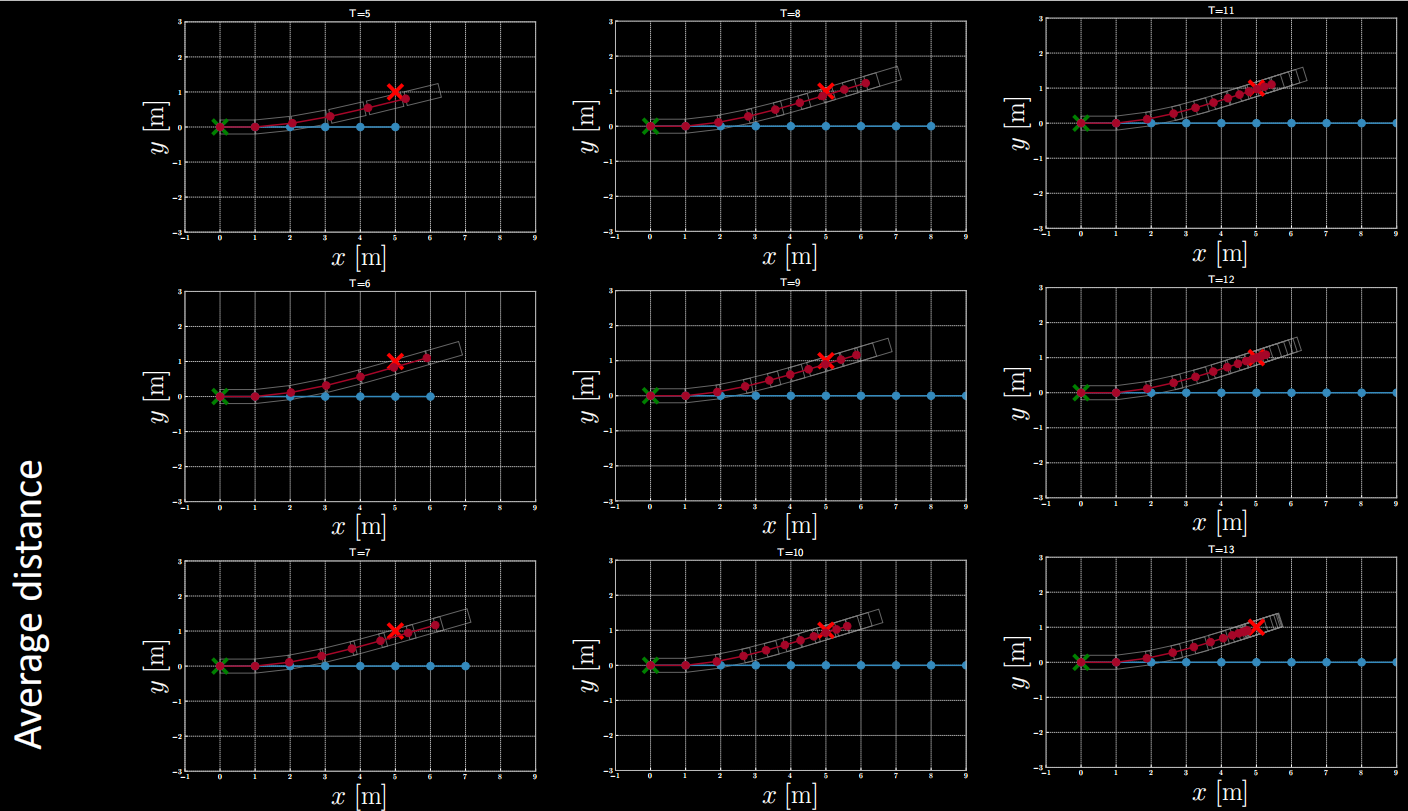
Figure 15 : Exemple de coût : distance moyenne

Exemple de coût de $(2)$ : Softmin

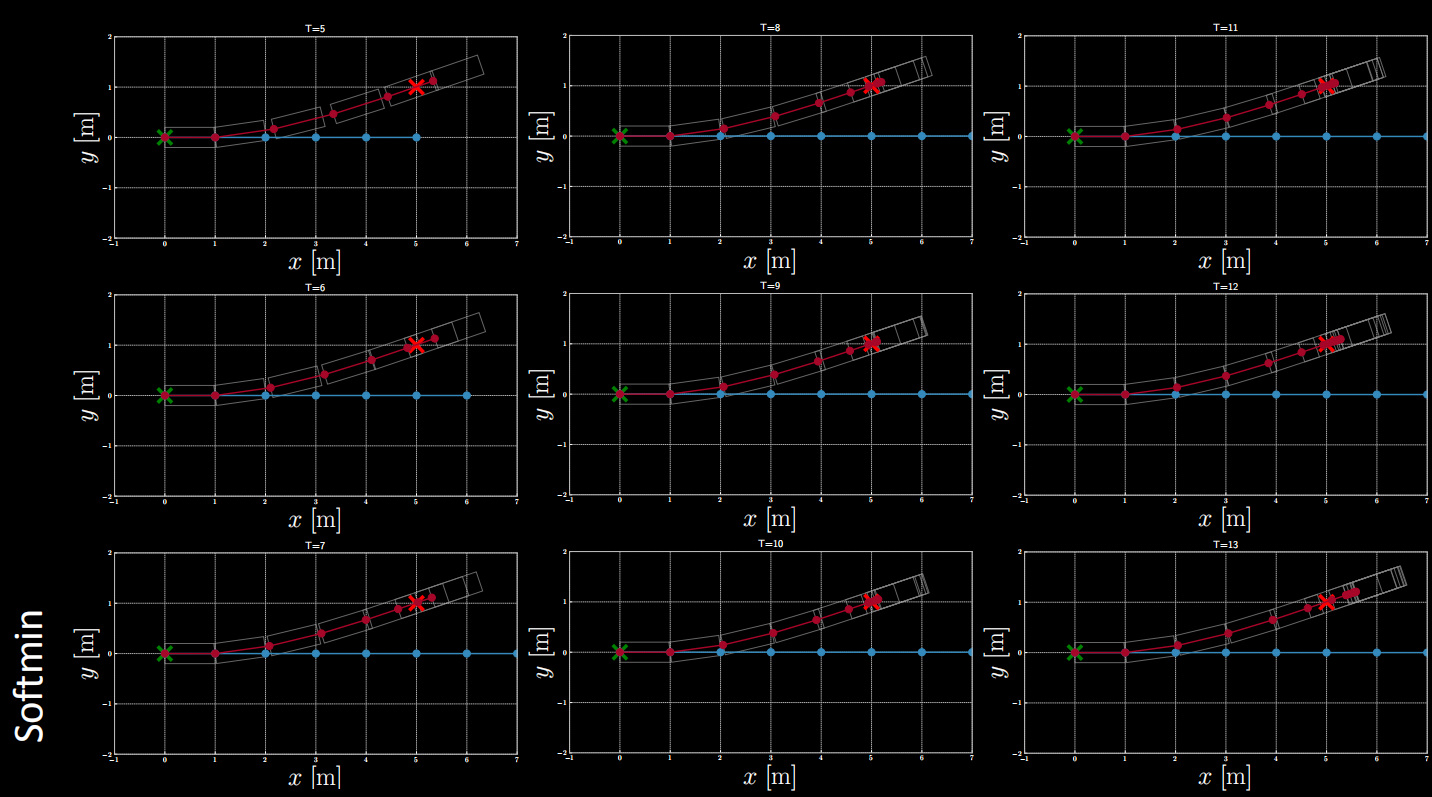
Figure 16 : Exemple de coût : softmin

Différentes formes de fonctions de coût peuvent être explorées par l’expérimentation.

Notebook Optimisation_Path_Planner

Dans ce notebook, nous utilisons également le tricycle comme exemple.

Définir le modèle cinématique d’un tricycle $\dot{\vx}=f(\vx,\vu)$

• $\vx$ représente l’état : ($x$, $y$, $θ$, $s$)
• $\vu$ représente le contrôle : ($ϕ$, $a$)
• On donne $\vx[t-1]$ et $\vu[t]$ pour obtenir l’état suivant $\vx[t]$

def f(x, u, t=None):
    L = 1  # m
    x, y, θ, s = x

    ϕ, a = u
    f = torch.zeros(4)
    f[0] = s * torch.cos(θ)
    f[1] = s * torch.sin(θ)
    f[2] = s / L * torch.tan(ϕ)
    f[3] = a
    return f

Définir plusieurs fonctions de coût

Comme mentionné ci-dessus, les fonctions de coût peuvent prendre différentes formes. Dans ce notebook, nous en listons 5 sortes comme suit :

• vanilla_cost : se concentre sur la position finale
• cost_with_target_s : se concentre sur la position finale et la vitesse zéro finale
• cost_sum_distances : se concentre sur la position de chaque étape, et minimise la moyenne des distances
• cost_sum_square_distances : se concentre sur la position de chaque étape, et minimise la moyenne des distances au carré
• cost_logsumexp : la distance de la position la plus proche doit être minimisée

def vanilla_cost(state, target):
    x_x, x_y = target
    return (state[-1][0] - x_x).pow(2) + (state[-1][1] - x_y).pow(2)

def cost_with_target_s(state, target):
    x_x, x_y = target
    return (state[-1][0] - x_x).pow(2) + (state[-1][1] - x_y).pow(2)
                                       + (state[-1][-1]).pow(2)

def cost_sum_distances(state, target):
    x_x, x_y = target
    dists = ((state[:, 0] - x_x).pow(2) + (state[:, 1] - x_y).pow(2)).pow(0.5)
    return dists.mean()

def cost_sum_square_distances(state, target):
    x_x, x_y = target
    dists = ((state[:, 0] - x_x).pow(2) + (state[:, 1] - x_y).pow(2))
    return dists.mean()

def cost_logsumexp(state, target):
    x_x, x_y = target
    dists = ((state[:, 0] - x_x).pow(2) + (state[:, 1] - x_y).pow(2))#.pow(0.5)
    return -1 * torch.logsumexp(-1 * dists, dim=0)

Définir la planification du chemin avec le coût

• L’optimiseur est défini comme étant la SGD.
• L’intervalle de temps T est fixé à 1s.
• Nous devons calculer chaque état à partir de l’état initial avec le code suivant :

• x = [torch.tensor((0, 0, 0, s),dtype=torch.float32)]
  for t in range(1, T+1):
    x.append(x[-1] + f(x[-1], u[t-1]) * dt)
  x_t = torch.stack(x)
  

• Ensuite, nous calculons le coût :

  cost = cost_f(x_t, (x_x, x_y))
  costs.append(cost.item())
  

• Implémentations de la rétropropagation et mise à jour de $\vu$.

  optimizer.zero_grad()
  cost.backward()
  optimizer.step()
  

• Maintenant, nous pouvons fournir des valeurs à path_planning_with_cost pour obtenir des résultats d’inférence et tracer des trajectoires. Exemple :

  path_planning_with_cost(
      x_x=5, x_y=1, s=1, T=5, epochs=5,
      stepsize=0.01, cost_f=vanilla_cost, debug=False
  )