과적합과 정규화

과적합^Overfitting

회귀 문제에서, 어떤 모델은 과소적합^underfit, 적합^right-fit 또는 과적합^overfit할 수 있다.

모델이 지니는 데이터에 대한 표현력이 충분하지 않으면, 모델은 과소적합할 것이다. 만일 모델이 데이터보다 높은 표현력을 갖는다면 (심층 신경망^{deep neural networks}의 경우와 같이), 과적합의 위험이 있다.

이 경우, 모델은 원본 데이터 그리고 노이즈^noise에 딱 맞게 학습할 만큼 강력해서, 당면한 과제에 대한 잘못된 해결책을 제시한다.

이상적으로 우리는 모델이 노이즈가 아닌 데이터 자체에 대해 학습하여, 데이터에 적합한 해결책이 되기를 원한다. 특히 이 과정에서 모델의 파워를 줄이는 것은 최소화하고자 한다. 딥러닝^{Deep learning} 모델은 굉장히 강력해서, 주어진 데이터를 학습하는데 꼭 필요한 정도보다 훨씬 더 높은 파워를 지니는 경우가 자주 발생한다. 우리는 (모델 훈련을 더 쉽게 하기 위해) 그 파워를 유지하고 싶지만, 동시에 과적합의 위험과 싸우고 있다.

디버깅^debugging을 위한 과적합

과적합은 디버깅과 같은 몇몇 경우에 유용하게 사용될 수 있다. 훈련 데이터의 작은 하위 집합 (단일 배치 또는 임의의 노이즈 텐서의 경우라도)에 대해 네트워크를 테스트하고 해당 네트워크가 주어진 데이터에 과적합 할 수 있는지 확인할 수 있다. 만일 모델이 이 데이터를 학습하는데 실패한다면, 이는 네트워크에 버그가 있을 수 있다는 하나의 신호로 해석할 수 있다.

정규화

정규화를 도입해서 과적합을 방지할 수 있다. 정규화의 정도는 모델의 검증 성능에 영향을 끼칠 것이다. 너무 낮은 수준의 정규화는 과적합 문제를 해결하기에는 역부족이다. 지나치게 높은 수준의 정규화는 모델의 효율성을 떨어뜨릴 수 있다.

정규화 는 모델에 사전 지식^{prior knowledge}를 더해준다. 매개변수^parameters에 대한 사전 분포가 구체적으로 지정된다. 이는 학습 가능한 함수의 집합에 제약을 두는 역할을 한다.

정규화에 대한 Ian Goodfellow의 또 다른 정의:

정규화는 학습 오류가 아닌 일반화의 오류를 줄이고자하는 학습 알고리즘에 대한 수정^modification이다.

초기화^{Initialization} 기술

특정 분포에 다라 가중치를 초기화하여 네트워크의 매개변수에 대한 사전 분포를 선택할 수 있다. 하나의 옵션은 [Xavier 초기화]https://pytorch.org/docs/stable/nn.init.html#torch.nn.init.xavier_normal_)이다.

가중치 감소^decay 정규화

가중치 감소 정규화는 우리가 살펴볼 첫 번째 정규화 기술이다. 가중치 감소 정규화는 머신 러닝 분야에서는 널리 사용되나, 신경망 부문에서는 상대적으로 그 정도가 덜하다. 파이토치에서 가중치 감소 정규화는 옵티마이저^optimizer의 매개변수로써 제공된다. (SGD의 ‘weight_decay’ 매개변수 예시를 참고하기 바란다.)

가중치 감소 정규화는 다음과 같이 불리기도 한다:

• L2
• Ridge
• Gaussian prior

우리는 매개변수에 작용하는 목적함수를 고려할 수 있다:

그 후 다음과 같이 업데이트를 한다:

가중치 감소를 위해서 페널티^penalty 항을 추가한다:

다음과 같은 업데이트가 이루어진다.

이 업데이트의 새로운 항은 매개변수 $\theta$ 를 0으로 살짝 이동시켜서, 업데이트를 할 때마다 가중치에 약간의 “감소^decay“를 더하도록 한다.

L1 정규화

파이토치 optimizers의 옵션으로 제공된다.

L1 정규화는 다음과 같이 불리기도 한다:

• LASSO: Least Absolute Shrinkage Selector Operator
• Laplacian prior
• Sparsity prior

이를 라플라스 사전 확률 분포^{Laplace distribution prior}로 볼 때, 이 정규화는 가우스 분포^{Gaussian distribution} 보다 확률 질량^{probability mass}을 0에 가깝게 둔다.

위에서 본 것과 같은 동일한 업데이트로 시작해서 추가 페널티를 더하는 것으로 볼 수 있다:

다음과 같은 업데이트가 이루어진다

$L_2$ 가중치 감소와 다르게, $L_1$ 정규화는 매개변수 벡터의 길이를 균등하게 줄이는 대신에, 매개 변수 공간에서 축에 가까운 구성 요소를 “무력화시킨다(죽인다)^kill”.

드롭아웃^Dropout

드롭아웃은 훈련 중에 특정 갯수의 뉴런을 무작위로 0으로 설정한다. 이는 네트워크가 입력에서 출력까지의 단일한 경로를 학습하는 것을 방지한다. 마찬가지로, 신경망의 거대한 규모의 매개변수는 신경망이 효과적으로 입력을 기억할 수 있게 한다. 하지만 드롭아웃을 사용하면 이러한 현상이 발생하기 훨씬 어려워지는데, 드롭이웃이 매번 서로 다른 무한한 수의 네트워크를 효과적으로 훈련시키기 대문에 입력이 매 번 다른 네트워크에 투입되기 때문이다. 따라서 드롭아웃은 과적합^overfitting을 제어하는 강력한 방법이 될 수 있고, 입력의 작은 변화^variation에 대해 더욱 강건^robust하게 대응할 수 있다.

그림 1: 드롭아웃이 없는 네트워크

그림 2: 드롭아웃을 갖는 네트워크

파이토치에서는 뉴런의 무작위 드롭아웃 비율을 설정할 수 있다.

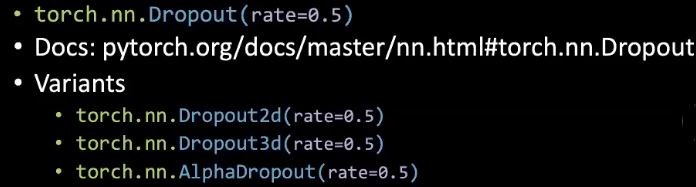
그림 3: 드롭아웃 코드

훈련이 끝난 뒤 추론 과정 중에 드롭아웃은 더 이상 사용되지 않는다. 추론을 위한 최종 네트워크를 생성하기 위해서, 드롭아웃이 이용된 모든 개별 네트워크에 대한 평균을 내고, 이를 추론에 사용한다. 마찬가지로 $p$ 이 드롭아웃 비율인 $1/1-p$ 을 모든 가중치에 곱할 수 있다.

조기 종료^{Early-stopping}

훈련 중에 검증 손실^{validation loss}가 증가하기 시작하면, 훈련을 중단시키고 지금까지 찾은 최선의 가중치를 사용할 수 있다. 이렇게 하면 가중치가 지나치게 증가하여 어느 시점에 검증 성능이 저하되는 것을 방지할 수 있다. 실제로 이 방법을 활용할 대에는 특정 간격으로 검증 성능을 계산하고, 검증 성능 개선이 이뤄지지 않는 경우가 특정 횟수가 되면 훈련을 조기 종료 시킨다.

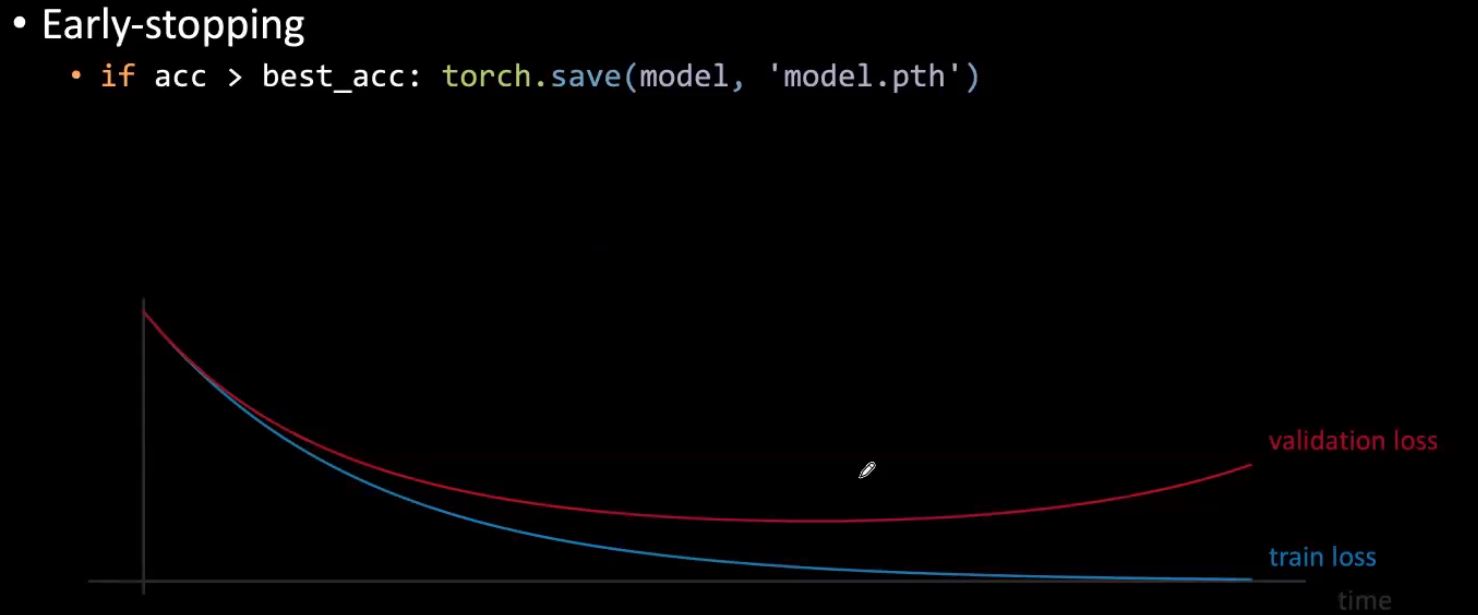
그림 4: 조기 종료

간접적으로 과적합에 맞서기

정규화로 볼 수는 없지만, 매개변수 정규화의 부작용^side-effect을 갖는 기술들이 있다.

배치-놈^Batch-norm

질문. 어떻게 배치-놈이 훈련을 효율적으로 만듭니까? 대답. 배치-놈을 적용할 때 더 높은 학습률을 사용할 수 있다.

배치 정규화는 신경망 내부의 공변량^covariate 이동을 방지하는데 사용되지만, 실제로 이게 수행이 되는지, 그리고 배치 놈의 실제적인 이점이 무엇인지에 대한 많은 논쟁이 있다.

그림 5: 배치 정규화

배치 정규화는 본질적으로 신경망 입력값을 정규화하는 논리를 전체 네트워크를 이루는 각 은닉층^{hidden layer}의 입력을 정규화하는 것으로 확장한다. 기본적인 아이디어는 후속 층(레이어)에 고정된 분포를 입력하는 것인데, 왜냐하면 고정 분포를 가질 때 학습이 가장 잘 발생하기 때문이다. 이를 위해 평균과 분산을 각 은닉층 이전에 계산하고, 이러한 배치 별 통계^{batch specific statistics}에 따라 들어오는 값을 정규화하여 훈련 중에 값이 이동하는 양을 줄인다.

이러한 정규화 효과와 관련해서, 각 배치의 다르기 때문에 개별 샘플은 배치에 따라 약간씩 다른 통계 값으로 정규화된다. 따라서 네트워크는 단일 입력에 대한 약간씩 변경된 버전을 볼 수 있게되고 이는 네트워크의 학습에 도움이 되며, 이는 과적합을 방지한다.

배치 정규화의 또 다른 이점은 훈련이 훨신 빠르다는 것이다.

더 많은 데이터

더 많은 데이터를 모으는 것은 과적합을 방지하는 쉬운 방법이지만, 이를 위한 비용이 많이 들거나, 혹은 불가능할 수도 있다.

데이터 증대시키기

Torchvision을 사용한 변환^{transformation}은 신경망이 미세한 변화^perturbation에 둔감해지는 방법을 배우도록해서 정규화의 효과를 거둘 수 있다.

그림 6: Torchvision을 이용한 데이터 증대

전이 학습^{Transfer Learning (TF) 미세 조정fine-tuning (FT)}

전이 학습(TF)은 사전 훈련된^pre-trained 네트워크 위에서 최종 분류기^{final classifier}를 훈련시키는 것을 말한다 (일반적으로 데이터가 거의 없는 경우에 사용된다).

미세 조정(FT)는 사전 훈련된 네트워크의 일부/전체 부분을 훈련시키는 것을 말한다 (일반적으로 많은 데이터를 가지고 있는 경우에 사용된다).

질문. 일반적으로 사전 훈련된 모델의 레이어를 언제 동결^freeze 해야 합니까? 대답. 훈련 데이터가 거의 없는 경우에.

4 개의 일반적인 케이스: 1) 비슷한 분포를 가진 데이터가 거의 없다면, 전이 학습을 할 수 있다. 2) 비슷한 분포를 가진 데이터를 많이 갖고 있다면, 특징 추출기^{feature extractor}의 성능 또한 향상시킬 수 있도록 미세 조정을 할 수 있다. 3) 데이터가 적고 분포도 다른 경우 특징 추출기에서 훈련된 최종 레이어 몇 개를 제거해야 하는데, 왜냐면 이 레이어들은 지나치게 전문적으로^{too specialized} 학습돼 있기 때문이다. 4) 데이터가 많고 분포도 다른 경우, 모든 부분을 훈련시킬^{train all portions} 수 있다.

성능 향상을 위해 레이어마다 다른 학습률을 사용할 수도 있다.

과적합과 정규화에 대한 논의를 더 진행하기 위해서 아래의 시각화된 내용을 살펴보자. 아래의 시각화는 다음의 노트북 코드로 만들어졌다.

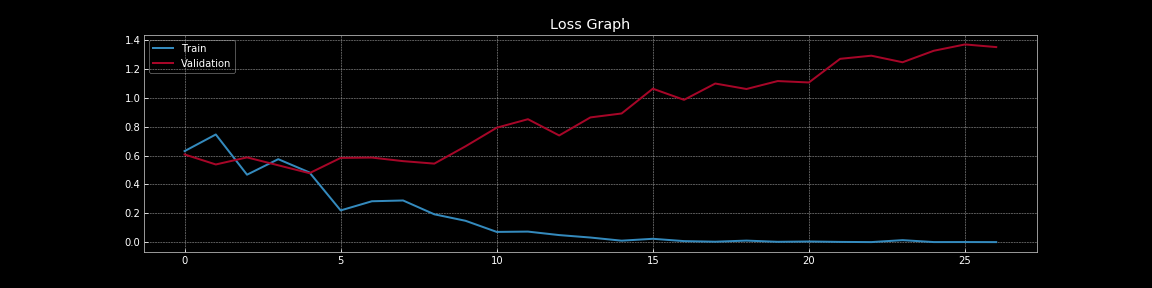
그림 7: 드롭아웃이 없을 때의 손실 곡선

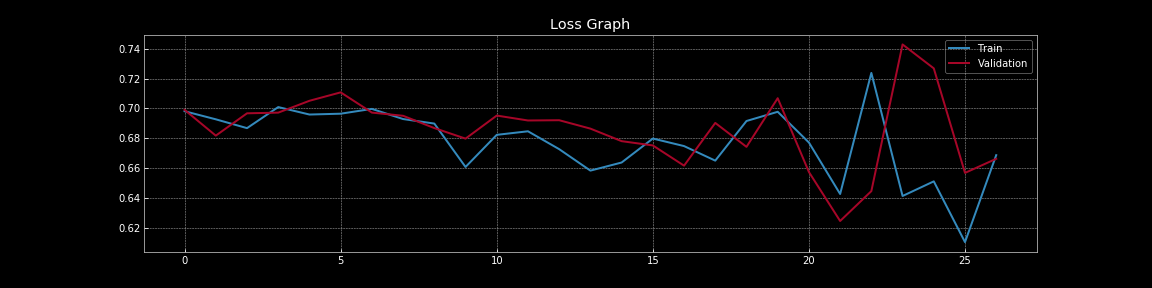
그림 8: 드롭아웃이 있을 때의 손실 곡선

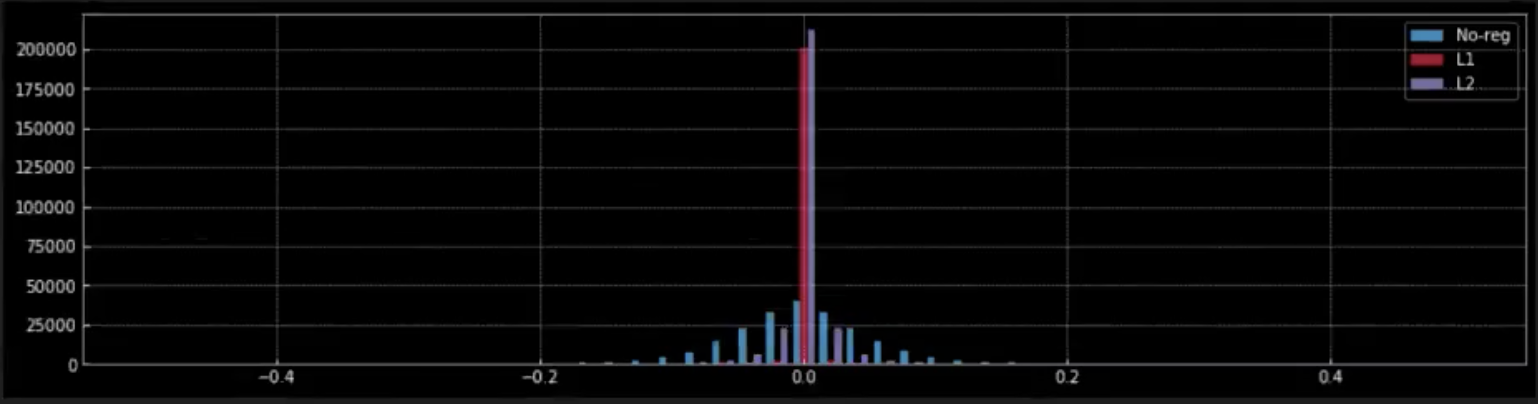
그림 9: 가중치에 대한 정규화의 효과

그림 7 부터 그림 8 을 통해서, 드롭아웃이 일반화 오류^{generalisation error}에 미치는 극적인 효과, 즉 훈련 손실과 검증 손실 차이,를 이해할 수 있다. 드롭아웃이 없는 그림 7 에서는 훈련 손실이 검증 손실보다 훨씬 낮기 때문에 명확한 과적합을 확인할 수 있다. 그러나 드롭아웃이 도입된 그림 8 에서는 훈련 손실과 검증 손실이 거의 연속적으로 겹치면서 모델이 표본 외 샘플^{out-of-sample} 데이터에 대한 지표^proxy 역할을 하는 검증 데이터에 잘 일반화 되고 있음을 나타낸다.

그림 9 에서는, 네트워크의 가중치에 미치는 (L1 및 L2) 정규화의 효과를 관찰한다.

• L1 정규화를 적용하면 0의 빨간색 꼭대기에서 대부분의 가중치가 0이라는 것을 알 수 있다. 0에 가까운 작은 빨간색 점들은 모델이 갖는 0이 아닌 가중치이다.

• 반대로, L2 정규화는 0에 가까운 라벤더 색 꼭대기에서 대부분의 가중치가 0에 가깝지만 0은 아닌 것을 알 수 있다.

• 정규화가 없는 (파란색) 경우, 가중치가 훨씬 더 유연하게 0 주위에 정규 분포와 유사한 모습으로 펼쳐진다.

베이지안 뉴럴 네트워크: 예측에 대한 불확실성 추정

네트워크의 예측에 대한 확신/확실성을 알아야 하므로 우리는 신경망의 불확실성에 대해 고려한다.

예시: (자동차, 배 등의)조종 장치^steering 제어를 위한 신경망을 구축한다면, 이 네트워크의 예측이 얼마나 확실한지 알아야 한다.

드롭아웃을 포함하는 신경망을 사용해서 예측에 대한 신뢰 구간^{confidence interval}을 얻을 수 있다. 드롭아웃 비율이 $r$ 인 네트워크를 훈련시켜 보자.

일반적으로 추론 중에 네트워크를 검증 모드^{validation mode}로 설정하고 최종 예측을 얻기 위해 모든 뉴런을 사용한다. 예측을 수행하는 동안 가중치 $\delta$ 를 $\dfrac{1}{1-r}$ 로 조정^{scale하여 훈련 중에 드롭아웃을 수행한다.}

이 방법은 개별 입력에 대해 단일한 예측을 제공한다. 그러나 예측에 대한 신뢰 구간을 얻으려면 동일한 입력에 대한 여러 예측이 필요하다. 따라서 추론 중에 네트워크를 검증 모드로 설정하는 대신에, 훈련 모드를 유지한다. 즉, 여전히 무작위로 뉴런을 탈락^drop 시키고 예측을 얻는 것이다. 이 드롭아웃 네트워크를 사용해서 여러번 예측을 수행할 때, 같은 입력에 대해서 탈락되는 뉴런에 따라 다른 예측을 얻는다. 이러한 예측을 사용하여 평균 최종 예측과 그 주변의 신뢰 구간을 추정한다.

아래 이미지에서는 네트워크 예측에 대한 신뢰구간을 추정했다. 이러한 시각화는 베이지안 신경망 노트북 코드로 만들어졌다. 빨간색 선은 예측을 나타낸다. 예측 주변의 보라색 음영 영역은 불확실성, 즉 예측의 분산을 나타낸다.

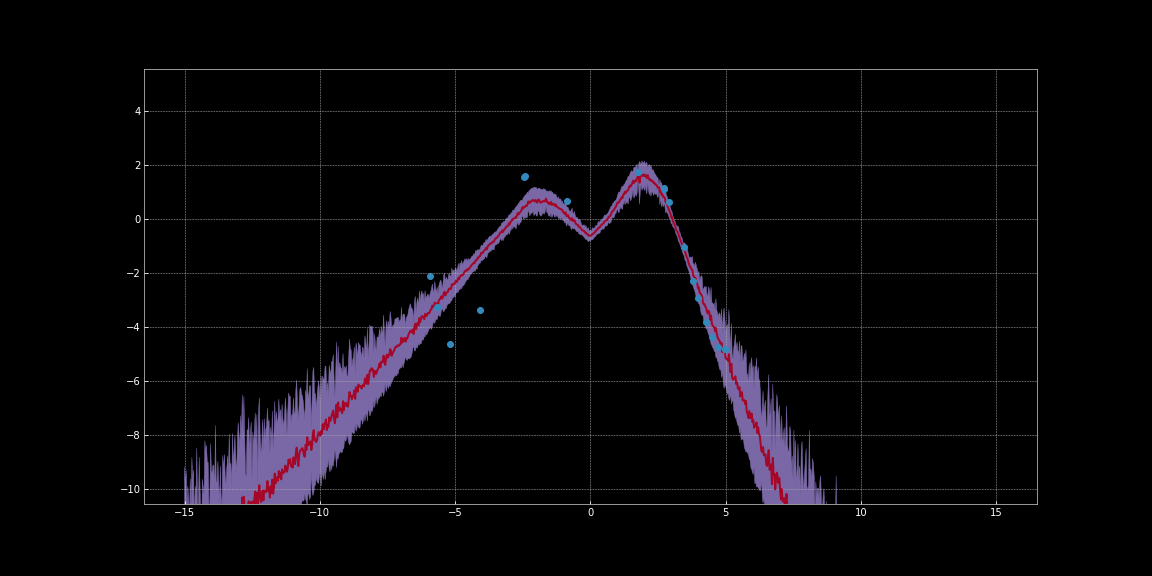
그림 10: ReLU 활성화^activation를 사용한 불확실성 추정

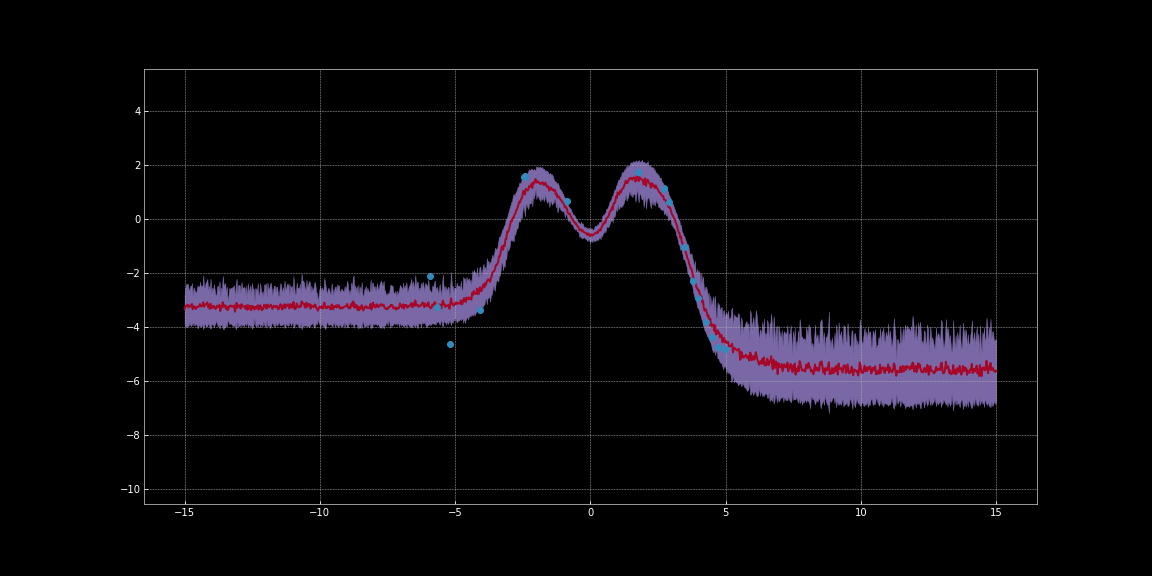
그림 11: Tahn 활성화를 사용한 불확실성 추정

위의 이미지에서 볼 수 있듯, 이러한 불확실성 추정치는 보정되지 않는다^{not calibrated}. 서로 다른 활성화 함수에 따라 달라지게 된다. 이미지에서는 데이터 주변의 불확실성이 확연히 낮다. 뿐만 아니라, 우리가 관찰 할 수 있는 분산은 미분할 수 있는 함수이다. 따라서 우리는 이 분산을 최소화하기 위해 경사하강법을 실행할 수 있다. 이를 통해 우리는 조금 더 확실한 예측을 얻을 수 있다.

EBM 모델에서 총 손실에 기여하는 여러 항^{multiple terms}이 있는 경우, 그들은 어떻게 상호작용 합니까?

EBM 모델에서는, 총 손실을 추정하기 위해 다른 항을 간단하게 편리하게 합산할 수 있다.

여담: 잠재 변수의 길이에 페널티를 주는 항은 모델에서 많은 손실 항 중 하나로 작동할 수 있다. 벡터의 길이는 대략적으로 차원의 수^{the number of dimensions}에 비례한다. 따라서 차원의 수를 줄이면 벡터의 길이가 줄어들고, 결과적으로 더 적은 정보가 인코딩된다. 오토 인코더^auto-encoder 환경에서는 이를 통해 가장 중요한 정보를 유지할 수 있도록 한다. 그러므로, 잠재 공간에서 정보를 압축^bottleneck하는 한 가지 방법은 잠재 공간의 차원을 줄이는 것이다.

정규화를 위한 하이퍼 파라미터^{hyper-parameter}를 어떻게 결정할 수 있습니까?

실제로 정규화를 위한 최적의 하이퍼-파라미터, 즉 정규화의 강도를 결정하기 위해서 우리는 다음의 방법을 이용할 수 있다.

• 베이지안 하이퍼-파라미터 최적화^{Bayesian hyper-parameter Optimization}
• 그리드 서치^{Grid Search}
• 랜덤 서치^{Random Search}

이러한 탐색을 수행하는 동안, 대체로 처음 몇 에폭^epochs이면 어떻게 정규화가 작동하는지 이해하기 충분하다. 따라서 모델을 광범위하게^extensively 훈련시킬 필요가 있다.