구조화된 예측을 위한 딥러닝

구조화된 예측

이것은 스칼라 이산 혹은 실수 값이 아닌 상호 의존적이고 종속적인 주어진 입력 x에 대해서 변수 y를 예측하는 문제이다. 출력 변수는 단일한 범주에 속하지 않지만, 지수^exponential 또는 무한개의 가능한 값을 가질 수 있다. 예시: 음성/필기 인식 또는 자연어 번역의 경우, 출력이 문법적으로 정확해야하고 가능한 출력 값의 갯수를 제한할 수 없다. 이 모델의 임무는 순차적, 공간적, 또는 조합적인 구조를 문제 영역 내에서 파악하는 것이다.

구조화된 예측에 대한 초기 작업

이 벡터는 모델 시스템의 경우 카테고리를 나타내는 소프트맥스와 비교할 수 있는 벡터를 내놓는 TDNN에 투입된다. 발음된 단어를 인식하는 때에 발생할 수 있는 문제점은 다른 사람들이 이 동일한 단어를 다른 방식과 속도로 발음할 수 있다는 것이다. 이 문제를 해결하기 위해 동적 시간 왜곡^{Dynamic Time Warping}이 사용된다.

이것은 누군가에 의해 기록한 시퀀스 또는 특징 벡터들에 대응하는 사전 기록된 템플릿 세트를 시스템에 제공하는 것이다. 신경망은 템플릿과 동시에 순련이 되므로 시스템은 서로 다른 발음의 단어를 인식하는 것을 학습한다. 잠재 변수를 사용하면 템플릿의 길이와 일치하도록 특징 벡터를 시간 왜곡할 수 있다.

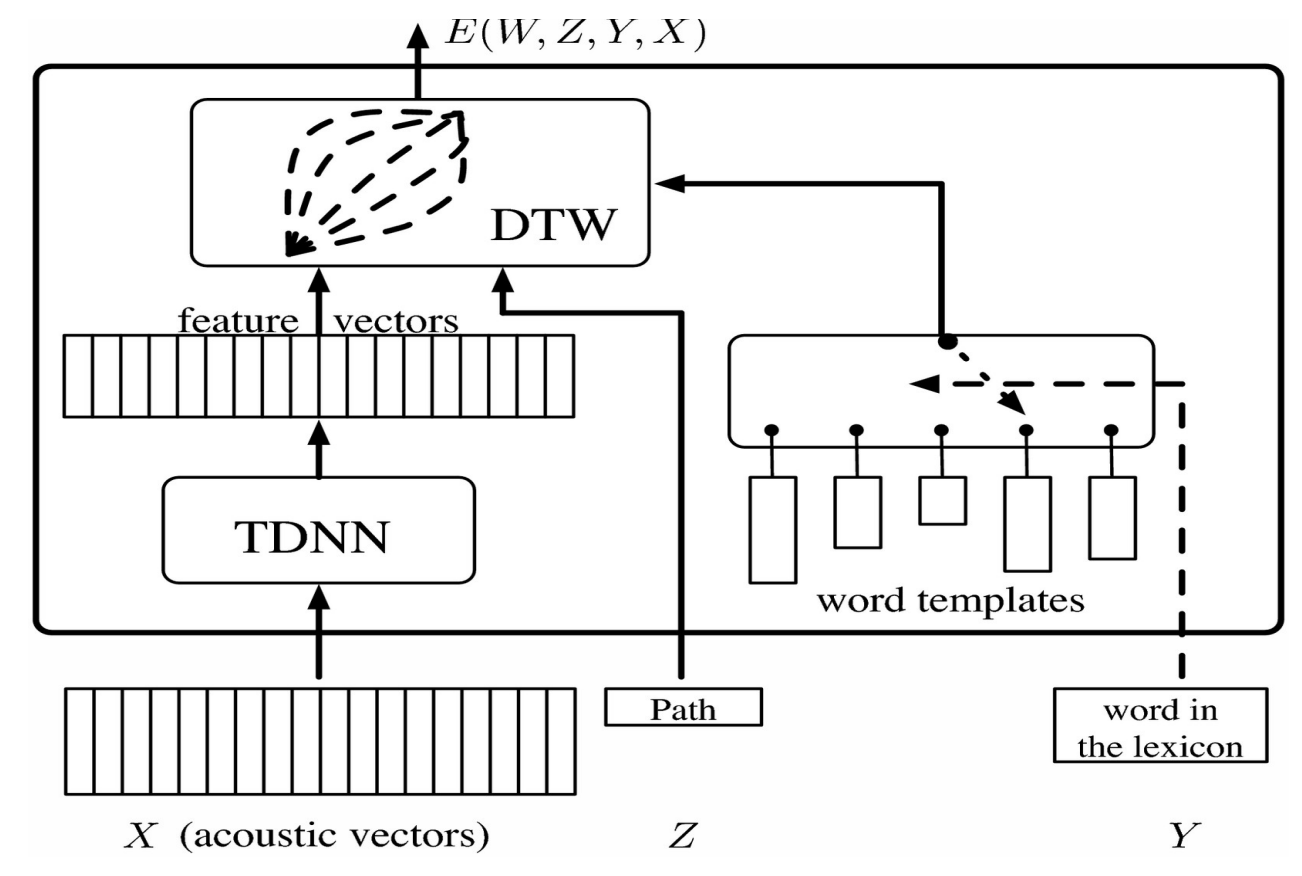
그림 1.

여기서 TDNN은 특징 벡터를 수평으로 배열하고 단어 템플릿을 수직으로 배열하는 행렬으로 시각화 될 수 있다. 행렬의 각 원소는 특징 벡터 사이의 거리에 해당한다. 이는 목표가 왼쪽 하단 모서리 부분에서 시작하고 오른쪽 상단 모서리 부분의 목표에 도달하기까지 거리값을 최소로 하는 경로를 지나는 그래프 문제로 시각화 될 수 있다.

이 잠재 변수 모델을 훈련시키려면 정답에 대한 에너지를 가능한한 작게 만들고 모든 오답에 대한 에너지를 더 크게 만들어야 한다. 이를 위해 우리는 틀린 단어를 입력 받아 현재의 특징 시퀀스에서 밀어내고 그래디언트를 역전파하는 목적 함수를 사용한다.

에너지 기반 요인 그래프

에너지 기반 요인 그래프의 기본 개념은 에너지가 모든 부분 에너지 항의 합이거나 확률이 요인들의 곱일 때 에너지 기반 모델을 만드는 것이다. 이러한 모델의 장점은 효율적인 추론 알고리즘을 이용할 수 있다는 점이다.

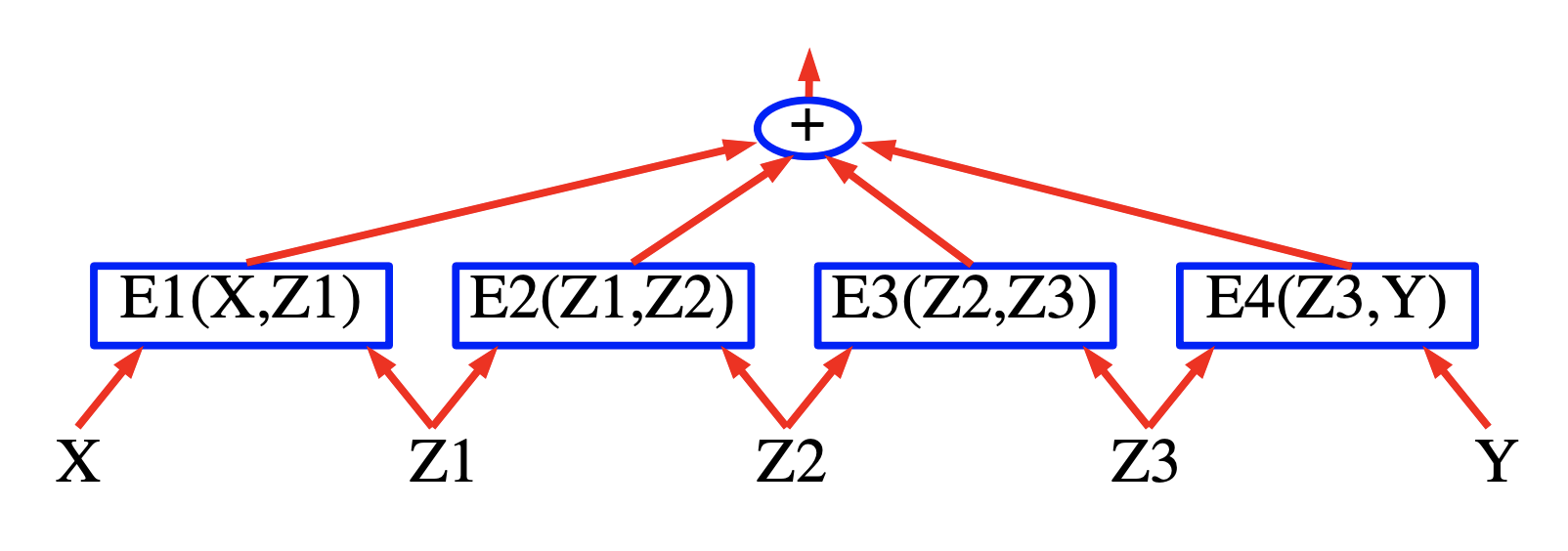
그림 2.

시퀀스 레이블링^labeling

모델은 입력 음성 신호 X를 가지고 출력 레이블이 총 에너지 항을 최소화 하도록 출력 레이블 Y를 내놓는다. <!–

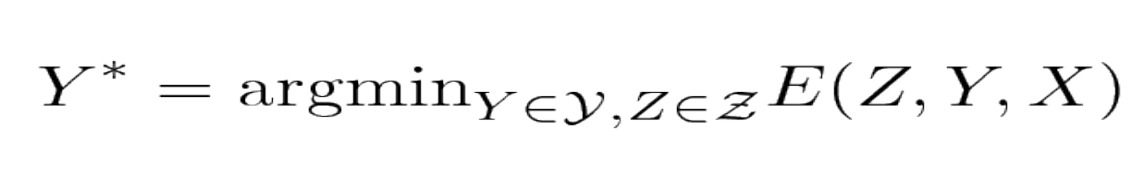
Figure 3.

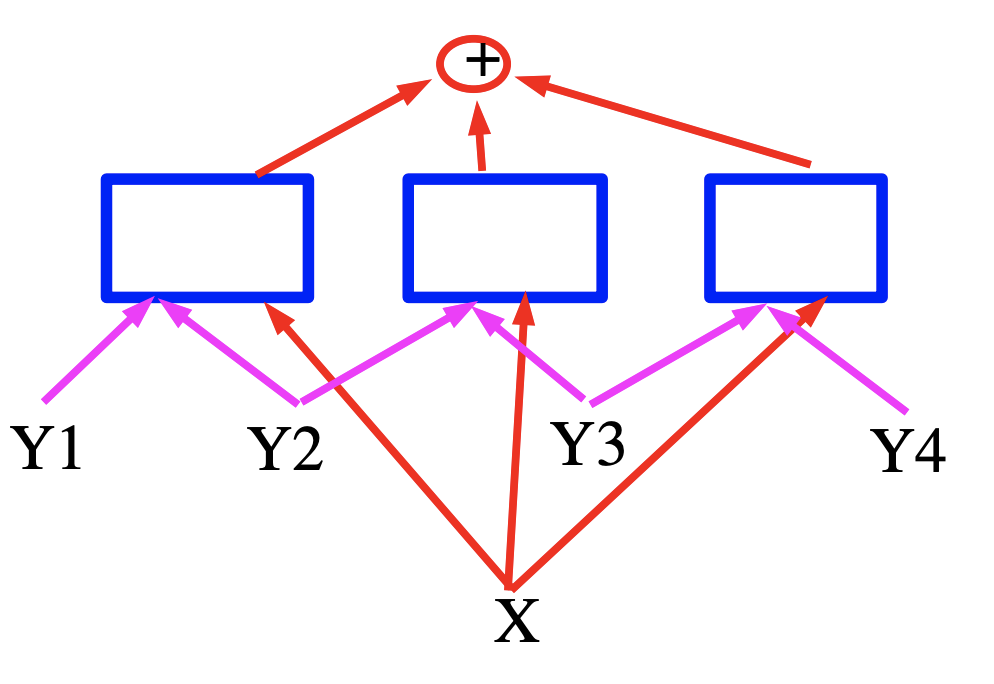
Figure 4.

–>

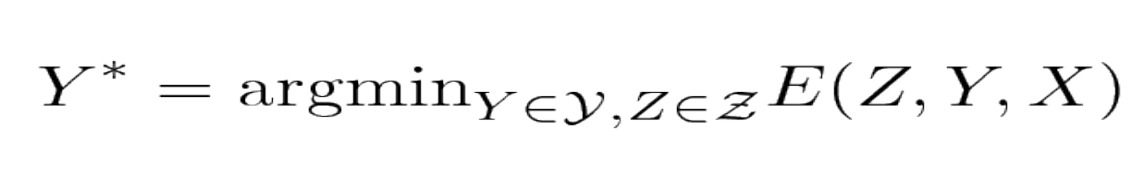
그림 3.

그림 4.

이 경우, 에너지는 주어진 입력 변수에 대해 특징 벡터를 출력하는 신경망인 파란색 사각형으로 표현된 세 개 항의 합이다. 음성 인식의 경우 X는 음성 신호로 생각할 수 있고, 사각형은 문법적 제약을 구현하고 Y는 생성된 출력 레이블을 나타낸다.

에너지 기반 요인 그래프를 위한 효율적인 추론

에너지 기반 학습에 대한 튜토리얼^tutorial(얀 르쿤, Sumit Chopra, Raia Hadsell, Marc’Aurelio Ranzato, and Fu Jie Huang 2006):

에너지 기반 모델을 이용한 학습 및 추론은 출력 집합 $\mathcal{Y}$ 와 잠재변수 $\mathcal{Z}$ 에 대한 에너지 최소화를 포함한다. $\mathcal{Y}\times \mathcal{Z}$ 의 값이 크면 이 최소화는 해결하기 어려워질 수 있다. 이 문제에 대한 한 가지 접근 방식은 최소화를 효율적으로 수행하기 위해 에너지 함수의 구조를 이용하는 것이다. 이 구조가 활용될 수 있는 한 가지 사례로는 에너지가 각각 Y 와 Z에서 다른 하위 집합에 의존하는 개별 함수(요인이라고 불림)의 합으로 표현될 때이다. 이러한 종속성은 요인 그래프의 형태로 가장 잘 표현된다. 요인 그래프는 그래픽 모델^{graphical models}, 또는 빌리프 네트워크^{belief networks}의 일반적인 형태이다.

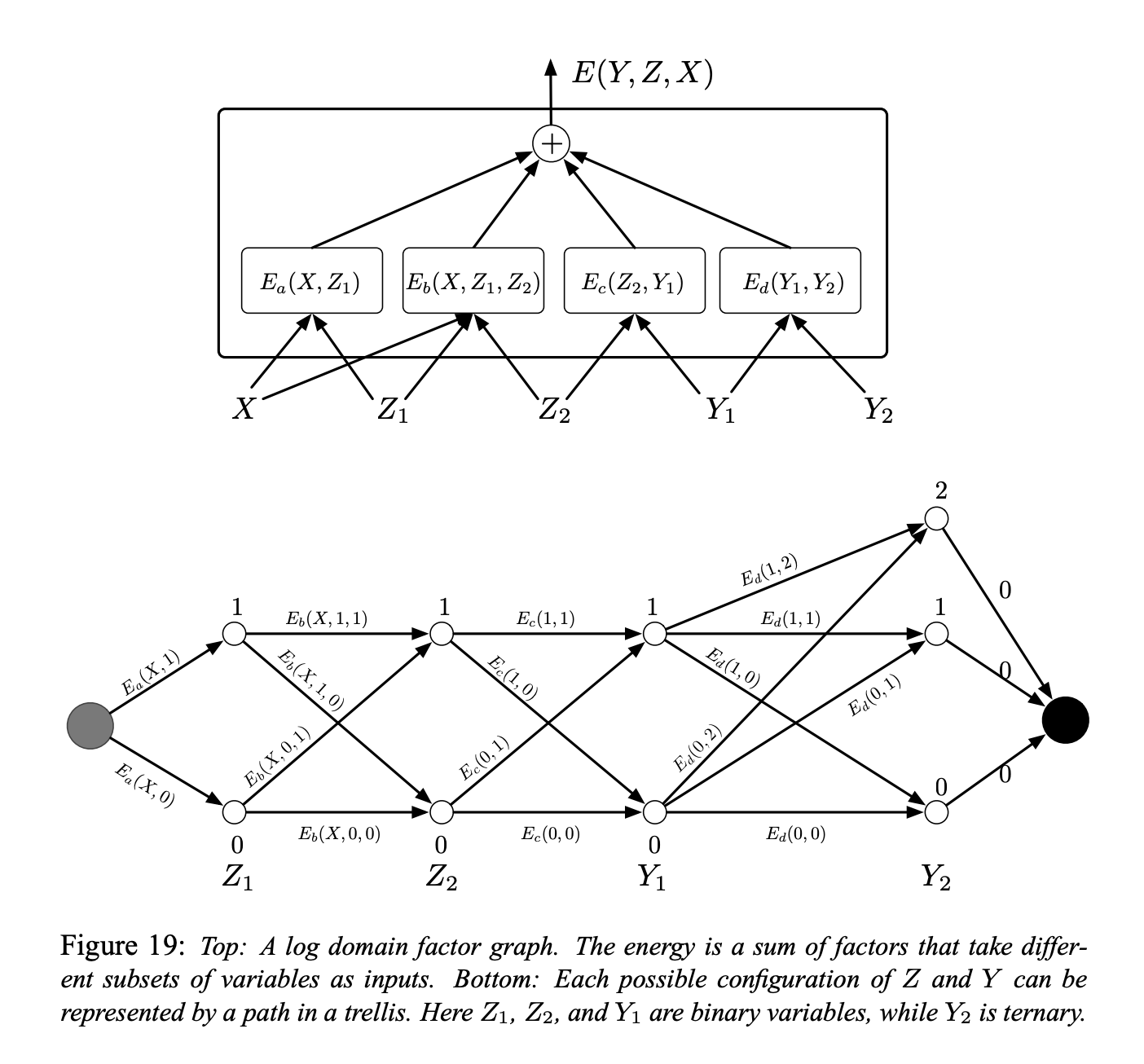
그림 5. (Figure 19)

요인 그래프의 간단한 형태는 Figure 19 (상단)에 나와 있다. 에너지 함수는 다음과 같은 네 개 요인의 합이다:

여기서 $Y = [Y_1, Y_2]$ 은 출력 변수이고 $Z = [Z_1, Z_2]$ 는 잠재 변수이다. 각 요인은 입력 변수 값들 사이의 소프트 제약^{soft constraints}을 나타내는 것으로 볼 수 있다. 추론 문제는 다음을 찾아내는 것으로 구성된다:

$Z_1$, $Z_2$, 그리고 $Y_1$ 가 이산 이진 변수이고, $Y_2$ 가 삼진^ternary 변수라고 가정하자. X는 항상 관찰되기 때문에 도메인 $X$ 의 카디널리티^cardinality는 중요하지 않다. X가 주어진 경우에 $Z$ 와 $Y$ 의 가능한 구성 수는 $2 \times 2 \times 2 \times 3 = 24$ 가 된다. 완전 탐색^{exhaustive search}를 통한 단순한 알고리즘은 전체 에너지 함수를 24번 평가한다 (96개의 단일 요인 평가).

그러나 주어진 $X$에 대해서 $E_a$는 $Z_1 = 0$ 와 $Z_1 = 1$ 의 오직 두 개의 가능한 입력 구성을 갖는다. 마찬가지로, $E_b$ 와 $E_c$ 는 단 4개의 가능한 입력 구성이 있고, $E_d$ 는 6개를 갖는다. 따라서 $2 + 4 + 4 + 6 = 16$ 회 이상의 단일 요인 평가는 필요하지 않다.

그러므로, 16개 요인 값을 미리 계산해서, Figure 19 (아래)에서 보이는 것과 같이 격자 형태의 호에 배치할 수 있다.

각 열의 노드^node는 단일 변수의 가능한 값을 나타낸다. 각 에지^edge는 입력 변수의 해당 값에 대한 요인의 출력 에너지에 의해 가중치가 부여된다. 이 표현에서 시작 노드에서 끝 노드까지의 단일한 경로는 모든 변수의 가능한 구성을 나타낸다. 경로의 가중치 합은 해당 경로에 대응하는 변수 구성의 총 에너지와 같다. 따라서, 추론 문제는 이 그래프에서 최단 경로를 찾는 것으로 축소될 수 있다. 이는 Viterbi 알고리즘이나 A* 알고리즘과 같은 동적 프로그래밍 기법으로 수행할 수 있다. 문제 해결에 드는 비용은 일반적으로 경로 갯수보다 지수적으로 작은 값인 에지의 갯수(16)에 비례한다.

$E(Y, X) = \min_{z\in Z} E(Y, z, X)$ 를 계산하기 위해 동일한 절차를 따르지만, 정해진 $Y$ 값과 호환되는 호^arcs의 하위 집합으로 그래프를 제한한다.

위의 방식은 때때로 min-sum 알고리즘이라고 불리고, 그래프 모델을 위한 전통적인 max-product의 로그 도메인 버전이다. 이 방식은 요인이 두 개 이상의 변수를 입력으로 받는 요인 그래프, 그리고 체인 구조 대신 트리 구조를 갖는 요인 그래프로 쉽게 일반화 될 수 있다.

그러나, 이는 (루프가 없는) 이분 트리^{bipartite trees}인 요인 그래프에만 적용된다. 만일 그래프에 루프가 존재하면, min-sum 알고리즘은 반복이 되었을 때 대략적인 해답을 제공하거나, 아예 수렴하지 않을 수 있다. 이러한 경우 모사 어닐링^{simulated annealing}과 같은 하강 알고리즘을 사용할 수 있다.

“얕은^Shallow” 요인을 갖는 단순 에너지 기반 요인 그래프

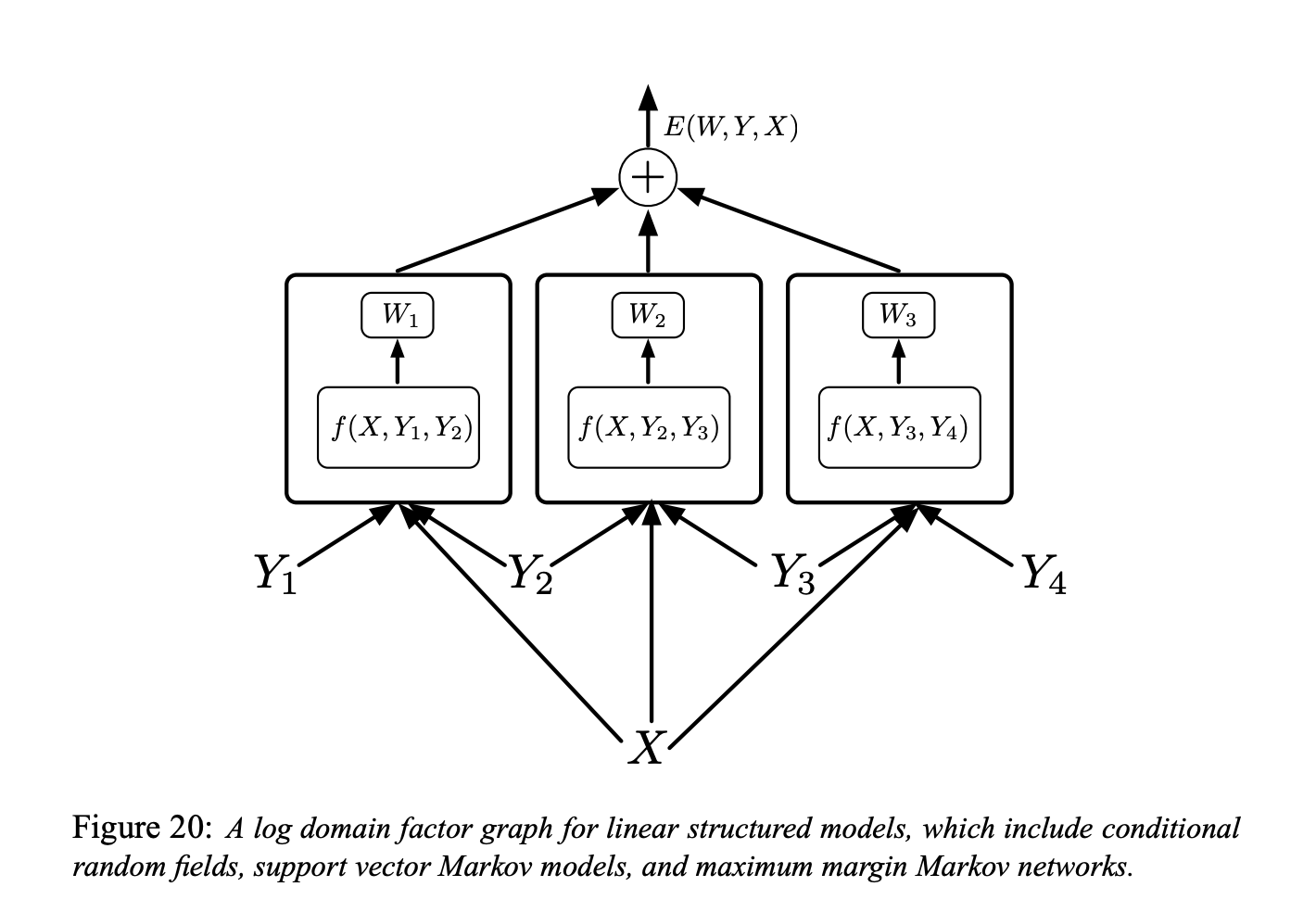
그림 6.

The factor graph shown in Figure 20 is a log domain factor graph for linear structured models (“simple energy-based factor graphs” we are talking about) Figure 20에 표시된 요인 그래프는 선형 구조화된 모델 (우리가 이야기하는 “단순 에너지 기반 요인 그래프”)에 대한 로그 도메인 요인 그래프이다.

여기서 $\mathcal{F}$ 는 요인 집합 (직접적인 상호 작용을 갖는 개별 레이블 쌍 집합)을 나타내고, $W_{m n}$ 은 요인 $(m, n),$ 에 대한 매개 변수 벡터이고, f_{m n}\left(X, Y_{m}, Y_{n}\right)$ 는 (고정된) 특징 벡터이다. 전역 매개 변수 벡터인 $W$ 는 모든 $W_{m n}$ 을 연결한 것이다.

다음으로는 어떤 유형의 손실 함수에 대해 생각해 볼 수 있다. 여기에 몇 가지 다양한 모델이 있다.

조건부 랜덤 필드^{Conditional Random Field}

음의 로그 우도^{negative log-likelihood} 손실 함수를 이용해서 선형 구조화된 모델을 훈련시킬 수 있다.

이것은 조건부 랜덤 필드이다.

직관적으로 생각하면 우리는 정답의 에너지가 낮고 좋은 답을 포함한 모든 답에 대한 지수 로그가 크길 바란다.

다음은 음의 로그 우도 손실 함수에 대한 공식적인 정의이다:

최대 마진 마르코프 넷과 잠재 SVM^{Max Margin Markov Nets and Latent SVM}

최적화를 위해 힌지^hinge 손실 함수도 사용할 수 있다.

이를 뒷받침하는 직관은 우리는 정답의 에너지가 낮은 값이길 바라고, 가능한 모든 오답 구성 중에서 가장 낮은 에너지를 갖는 것을 모든 오답 또는 나쁜 답 중에서 찾아낼 것이다. 그 다음 우리는 이것의 에너지를 밀어 올릴 것이다. 다른 오답에 대해서는 에너지 값을 밀어 올릴 필요가 없는데, 왜냐하면 이것들은 어짜피 더 큰 값을 지니기 때문이다.

이것이 최대 마진 마르코프 넷과 잠재 SVM의 기본이 되는 아이디어이다.

구조화된^structured 퍼셉트론^perceptron 모델

퍼셉트론 손실을 이용해서 선형 구조 모델을 훈련시킬 수 있다.

Collins [Collins, 2000, Collins, 2002]는 다음과 같은 NLP 맥락에서의 선형 구조 모델 사용을 옹호했다.

여기서 $Y^{* i}=\operatorname{argmin}_{y \in \mathcal{Y}} E\left(W, y, X^{i}\right)$ 는 시스템에서 생성된 답이다.

음성/필기 인식을 위한 식별^{discriminative} 훈련의 초기 여정

최소 경험적 오류 손실^{Minimum Empirical Error Loss} (Ljolje 와 Rabiner 1990):

시퀀스 수준에서 훈련을 시킴으로써 그들은 시스템에 특정한 소리 또는 위치를 알려주지 않는다. 그들은 시스템에 입력 문장과 그것이 단어 단위로 적힌 것은 제공하고, 시스템이 시간 왜곡^{time warping}을 통해 이것을 알아내도록 요청한다. 그들은 신경망을 사용하지 않았고 음성 신호를 소리 범주로 바꾸는 다른 방법을 가지고 있었다.

그래프 트랜스포머 넷^{Graph Transformer Net}

여기서의 문제는 우리가 가진 일련의 숫자 입력을 어떻게 분할해야 할 지 모른다는 것이다. 우리가 할 수 있는 것은 각 경로를 입력을 분할하는 방식에 대응되도록 그래프를 만드는 것이다. 그리고 여기에서 가장 낮은 에너지를 갖는 경로는 찾아내는데, 기본적으로 최단 경로는 찾는 것이다. 다음은 이것이 어떻게 동작하는지를 보여주는 구체적인 예시이다.

입력 이미지 34가 있다. 이것을 세그멘터(분할기)^segmenter에 투입하고 여러 개의 세분화된 대안을 얻는다. 이러한 분할은 사물의 덩어리를 그룹화하는 방식이다. 분할 그래프의 각 경로는 잉크 덩어리를 그룹화하는 특정한 방법에 해당한다. <!–

Figure 7.

–>

그림 7.

우리는 동일한 문자 인식 ConvNet을 통해 각각을 실행하고, 10개의 점수 목록(여기서는 2 이지만 기본적으로 10이어야 하고, 10개의 범주를 나타냄)을 얻는다. 예를 들어, 1 [0.1]은 범주 1의 에너지 값이 0.1 임을 나타낸다. 따라서 여기에 그래프가 생겼고, 이것을 특이한 형태의 텐서로 생각할 수 있다. 사실 희소^sparse 텐서이다. 이 텐서는 각각의 가능한 변수 구성에 대해 변수의 비용을 알려준다. 여기서 우리는 에너지에 대해 이야기 하고 있기 때문에, 이는 텐서의 분포 또는 로그 분포와 더 비슷한 모습을 보인다.

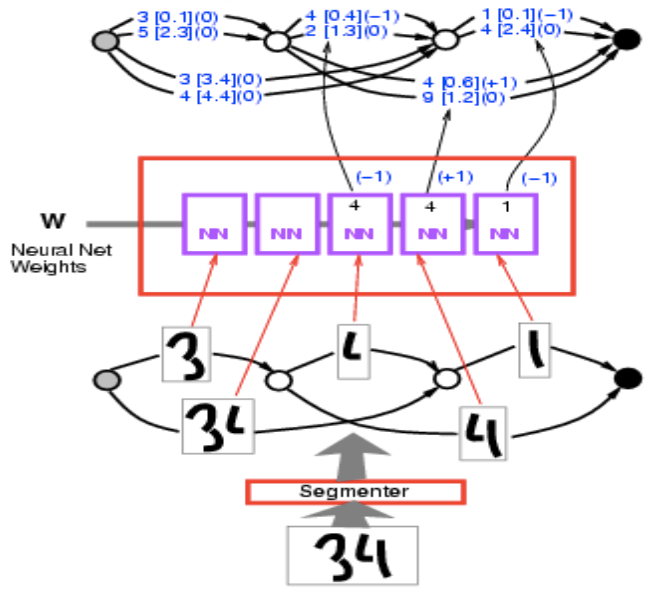
그림 8.

이 그래프에서 정답의 에너지를 계산하고 싶다. 정답은 34이다. 그 경로들 중에 34라고 말하는 것을 찾으면 두 개가 있다. 하나의 에너지는 3.4 + 2.4 = 5.8 이고, 다른 하나는 0.1 + 0.6 = 0.7 이다. 에너지가 가장 낮은 경로를 선택한다. 여기서 우리는 에너지 0.7의 경로를 얻는다.

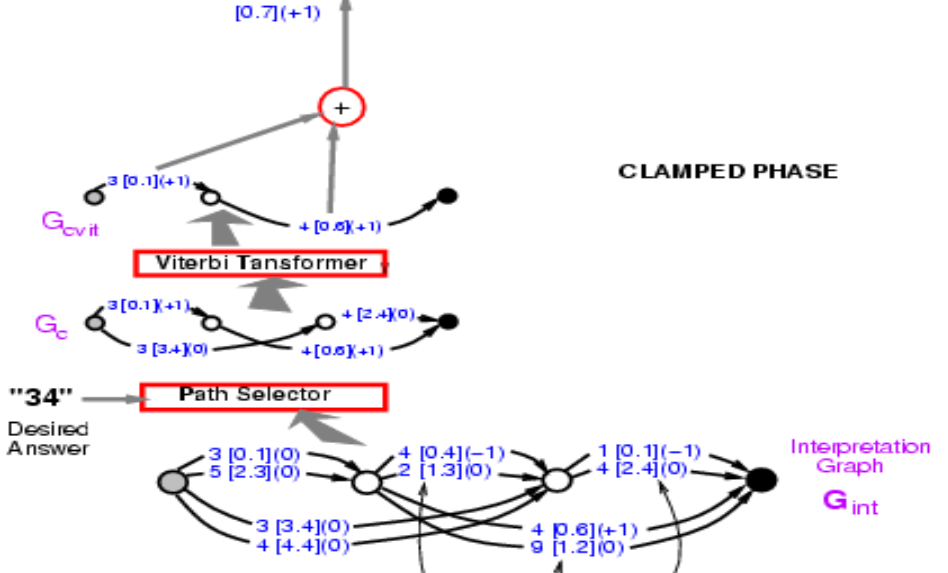
그림 9.

따라서 경로를 찾는 것은 잠재 변수가 선택한 경로인 상황에서 잠재 변수를 최소화 하는 것과 같다. 개념적으로 이것은 잠재 변수가 경로인 에너지 모델이다.

이제 우리는 정답 경로의 에너지 0.7을 얻었다. 이제 우리가 할 일은 이 전체 구조에 대해 기울기 역전파를 수행하여 최종 에너지가 줄어들도록 ConvNet의 가중치를 변경하는 것이다. 힘들 것 같지만 전적으로 가능한 이야기다. 왜냐하면 이 전체 시스템은 우리가 이미 알고 있는 요소로 만들어졌고, 보통의 신경망과 경로 선택기^{Path Selector} 그리고 Viterbi 트랜스포머는 기본적으로 특정한 에지를 선택하거나 선택하지 않는 스위치이다.

그렇다면 어떻게 역전파를 할까? 우선 점 0.7은 0.1과 0.6의 합이다. 따라서 점 0.1과 0.6 모두 괄호 안에 표시된대로 그래디언트 +1 을 갖을 것이다. Viterbi 트랜스포머는 이 두 경로 중에서 딱 하나를 선택한다. 따라서 입력 그래프의 해당 에지에 대한 그래디언트를 복사하고 선택되지 않은 다른 경로의 그래디언트 값을 0으로 설정한다. 이게 바로 Max-Pooling 또는 Mean-Pooling에서 일어나는 일이다. 경로 선택기는 동일하고, 단지 정답을 선택하는 시스템일 뿐이다. 이 단계에서 그래프의 3 [0.1] (0) 은 3 [0.1] (1) 이 되어야 하고, 나중에 이 부분으로 다시 돌아올 것이다. 그리고 신경망을 통해 그래디언트 역전파를 실행할 수 있다. 이는 정답의 에너지를 작게 만들 것이다.

여기서 중요한점은 이 구조가 동적^dynamic이라는 점인데, 만일 이 구조에 새로운 입력값을 제공하면, 신경망의 인스턴스 수가 분할^{segmentations} 갯수에 따라 변경되고 파생된 그래프 또한 바뀔 것이기 때문이다. 따라서 이러한 동적 구조를 통해 역전파를 해야 한다. 이 시점이 바로 PyTorch 등이 중요한 역할을 하는 부분이다.

이 시점의 역전파는 정답의 에너지를 작게 만든다. 그리고 오답의 에너지를 크게 만드는 또 다른 단계가 있을 것이다. 이 경우에 시스템이 원하는 답을 선택하도록 한다. 이것은 지각 손실^{perceptual loss}를 사용하는 간단한 형태의 판별 훈련^{discriminative training}이 될 것이다.

두 번째 단계 중 첫 번 째 단계는 첫 번째 단계와 정확히 동일하다. Viterbi 트랜스포머는 여기에서 가장 낮은 에너지를 갖는 최적의 경로를 고르고, 우리는 이 경로가 맞는지 틀린지 신경쓸 필요가 없다. 왜냐하면 이 에너지는 가능한 모든 경로 중 모두 작은 값이라서 첫 번째 단계에서 얻은 것과 같거나 작을 것이기 때문이다.

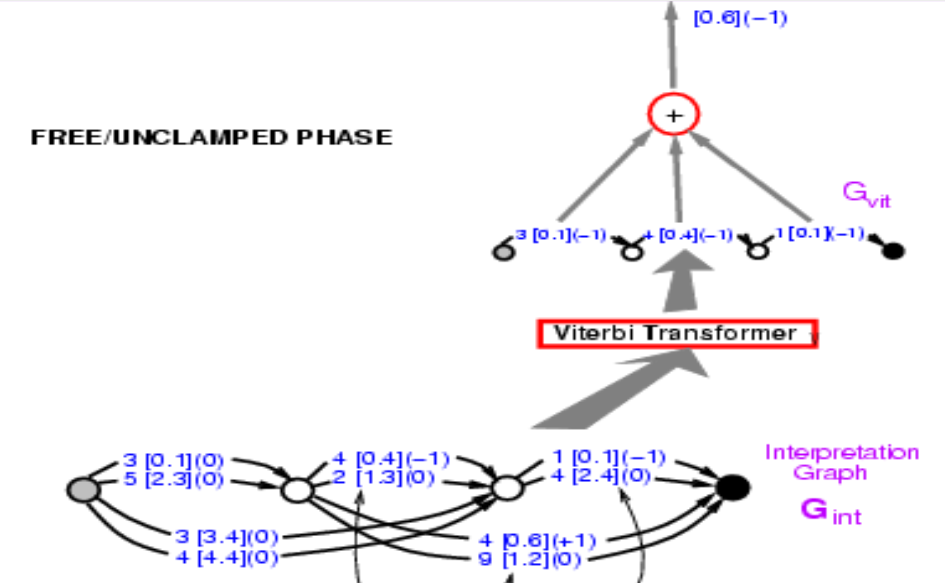
그림 10.

첫 번째 단계와 두 번째 단계를 합쳐보자. 손실 함수는 에너지1-에너지2 가 되어야 한다. 이전에는 왼쪽 부분을 통해 역전파 하는 방법을 소개했지만, 이제는 전체 구조를 통한 역전파를 해야한다. 어떤 경로든지 왼쪽에 위치하면 +1 을 얻을 것이고, 어떤 경로든 오른쪽에 위치한 것은 -1을 얻을 것이다. 따라서 양쪽 경로에서 모두 나타나는 3 [0.1] 는 그래디언트 0을 갖게 될 것이다. 이런 방식을 통해서 시스템은 결국 정답의 에너지와 가장 좋은 답의 에너지 간의 차이를 최소화한다. 여기서의 손실 함수는 퍼셉트론 손실^{perceptron loss}이다.

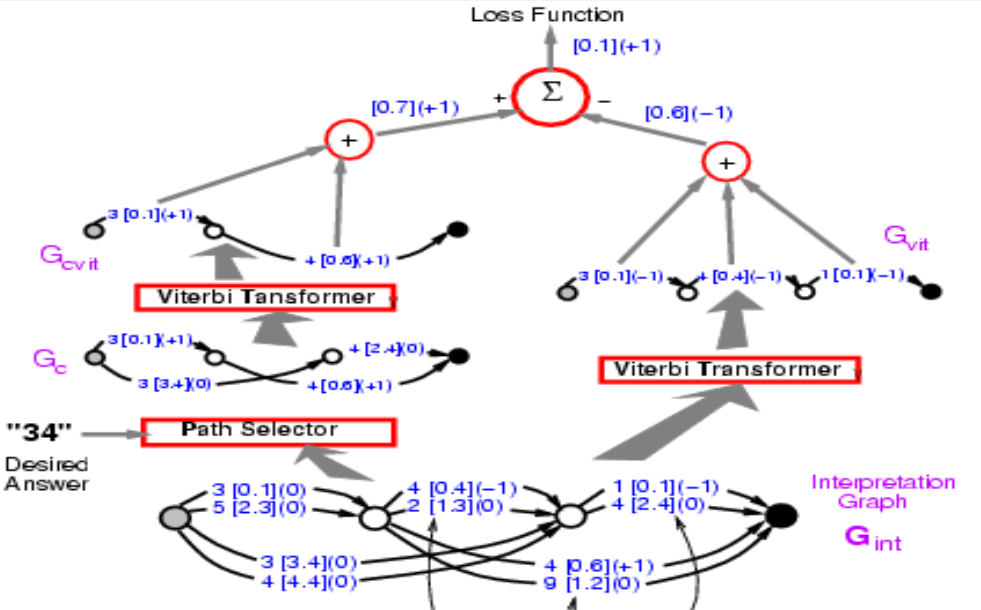
그림 11.

내용 이해와 관련된 질문과 대답

질문1: 에너지 기반 요인 그래프의 경우에 추론이 쉬운 이유가 무엇입니까?

잠재 변수가 있는 에너지 기반 모델의 추론에서는 에너지를 최소화 하기 위해 경사 하강법과 같은 기술을 이용하는 것을 포함하지만, 이 경우 에너지는 요인의 합이고 동적 프로그래밍과 같은 기술을 대신 사용할 수 있다.

질문2: 요인 그래프의 잠재 변수가 연속 변수이면 어떻게 됩니까? 이 경우에도 여전히 최소 합 알고리즘^{min-sum algorithm}을 사용할 수 있습니까?

이 경우 모든 요인 값에 대한 모든 가능한 조합의 경우를 탐색할 수 없기 때문에 불가능하다. 하지만, 이러한 경우, 독립적인 최적화를 할 수 있기 때문에 에너지는 우리에게 도움을 준다. $Z_1$ 와 $Z_2$ 의 조합은 그림 19의 $E_b$에만 영향을 준다. 그러므로 추론을 수행하기 위해 동적 프로그래밍과 독립적인 최적화를 할 수 있다.

질문3: NN 상자^{NN boxes}가 별도의 ConvNets를 참조합니까?

그것들은 서로 공유된다. 그것들은 동일한 ConvNet의 여러개 복사본이다. 단지 문자 인식 네트워크에 불과하다.