그래프 합성곱 신경망 III

그래프 합성곱 신경망 개요 ^{Introduction to Graph Convolutional Network (GCN)}

그래프 합성곱 네트워크는 데이터 구조를 활용하는 아키텍쳐 유형 중 하나이다. 세부 사항으로 들어가기 전에, GCN과 셀프-어텐션^{self-attention}은 개념적으로 관련이 있으므로 셀프-어텐션에 대해 간단히 복습해보자.

복습: 셀프-어텐션

• 셀프-어텐션에서는 입력값 집합 $\lbrace\boldsymbol{x}_{i}\rbrace^{t}_{i=1}$ 을 갖는다. 시퀀스와 다르게 셀프-어텐션은 순서가 없다.
• 집합 안에 벡터들의 선형결합에 의해 은닉 벡터 $\boldsymbol{h}$가 주어진다.
• 이를 행렬 벡터 곱셈을 사용해 $\boldsymbol{X}\boldsymbol{a}$로 표현이 가능하며, $\boldsymbol{a}$는 입력벡터 $\boldsymbol{x}_{i}$에 상응하는 차수^coefficient를 갖는다.

더 자세한 설명은, Week 12에서 참조 가능하다.

표기법

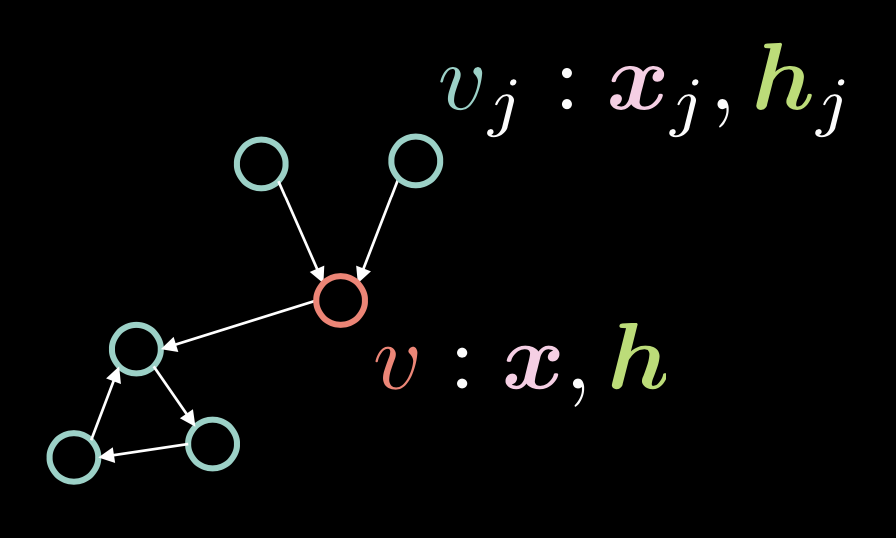
Fig. 1: 그래프 합성곱 그래프

Figure 1에 보여지는 것과 같이, 정점 $v$는 두 개의 벡터 (입력값 $\boldsymbol{x}$ 와 은닉 표현 $\boldsymbol{h}$) 로 이루어져있다. 다수의 정점 $v_{j}$ 또한 $\boldsymbol{x}_j$ 와 $\boldsymbol{h}_j$로 이루어져있고, 그래프에는 정점들이 유향 엣지^{directed edge: 간선}들로 연결되어있다.

이러한 유향 엣지는 인접 벡터^{adjacency vector} $\boldsymbol{a}$로 표현이 가능하며, 유향 엣지가 $v_{j}$에서 $v$로 향한다면 각 요소 $\alpha_{j}$는 $1$이 된다.

차수 (들어오는 엣지들의 수) $d$는 인접 벡터의 노름 ^normi.e. $\Vert\boldsymbol{a}\Vert_{1}$ 으로 정의되며, 이는 벡터 $\boldsymbol{a}$의 1의 수와 같다.

은닉 벡터 $\boldsymbol{h}$ 는 다음과 같이 주어진다:

$f(\cdot)$는 ReLU $(\cdot)^{+}$, 시그모이드 Sigmoid $\sigma(\cdot)$, 쌍곡탄젠트 $\tanh(\cdot)$와 같은 비선형 함수^{non-linear function}이다.

$\boldsymbol{U}\boldsymbol{x}$는 회전 $\boldsymbol{U}$를 입력값 $v$에 적용함으로 정점^vertex $v$를 다룬다. 셀프-어텐션에서 기억해야 할 것은 은닉 벡터 $\boldsymbol{h}$는 $\boldsymbol{X}\boldsymbol{a}$에서 계산되고, 이는 $\boldsymbol{X}$에서의 열은 $\boldsymbol{a}$의 각 원소들에 의해 스케일링^scaled된다. GCN 맥락에서 이는 여러개의 수신 엣지들이 있을 때( 인접 벡터 $\boldsymbol{a}$ 안에 다수의 1들) $\boldsymbol{X}\boldsymbol{a}$값이 더욱 커지게 된다는 것을 뜻한다.

반면에, 수신 엣지가 하나라면, 위 값은 작아진다. 수신 엣지의 수에 비례하는 값의 문제를 수신 엣지의 수 $d$로 나누는 것으로 해결 가능하다. 그런 다음, $\boldsymbol{X}\boldsymbol{a}d^{-1}$에 회전 $\boldsymbol{V}$를 적용한다.

전체 입력 집합$\boldsymbol{x}$에 대해여 은닉표현 $\boldsymbol{h}$을 다음과 같은 행렬 표기법을 사용하여 표현 가능하다:

여기서 $\vect{D} = \text{diag}(d_{i})$.

Residual Gated GCN 이론과 코드

Residual Gated 그래프 합성곱 신경망은 Figure 2처럼 표현되는 GCN의 한 종류이다.

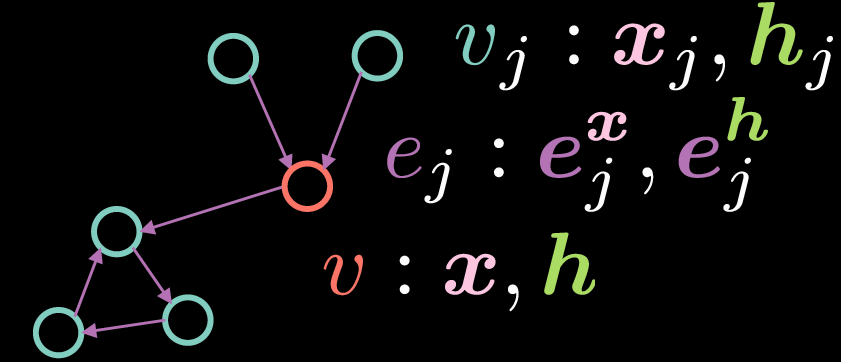
Fig. 2: Residual Gated Graph Convolutional Network

기본 GCN처럼, 정첨 $v$는 2개의 벡터 입력값 $\boldsymbol{x}$와 은닉 표현 $\boldsymbol{h}$ 갖는다. 하지만 이런 경우에는 엣지들 또한 특징 표현을 갖는다. 여기서 $\boldsymbol{e_{j}^{x}}$는 입력 엣지 표현을 나타내고, $\boldsymbol{e_{j}^{h}}$는 은닉 엣지 표현을 나타낸다.

정점 $v$의 은닉 표현 $\boldsymbol{h}$ 는 다음 방정식으로 계산된다:

여기서 $\boldsymbol{x}$는 입력 표현이고, $\boldsymbol{Ax}$ 는 입력값 $\boldsymbol{x}$에 적용된 회전^rotation을 나타내고, $\sum_{v_j→v}{\eta(\boldsymbol{e_{j}})\odot \boldsymbol{Bx_{j}}}$는 회전된 수신 특징^{incoming features} $\boldsymbol{Bx_{j}}$와 게이트 $\eta(\boldsymbol{e_{j}})$의 원소별 곱셈^{elementwise multiplication}의 합이다. 위에서 다룬 기본 GCN에서의 수신 표현들을 평균낸 것과 다르게, 게이트 항^term은 수신 표현들을 엣지 표현 기반으로 조절할 수 있게 하기에 게이트 항은 Residual Gated GCN을 구현하는데 매우 중요한 역활을 한다.

주의할 점은 합이 정점 $v$로 향하는 수신 엣지를 갖는 정점들 ${v_j}$만으로 이루어져 있다는 것이다. Residual Gated GCN에서의 단어 Residual은 은닉 표현 $\boldsymbol{h}$ 을 계산하기 위해 입력 표현 $\boldsymbol{x}$ 을 더했다는 것에서 비롯된다. 게이트 항 $\eta(\boldsymbol{e_{j}})$ 은 다음과 같이 계산된다:

게이트 값 $\eta(\boldsymbol{e_{j}})$는 수신 엣지표현들의 시그모이드를 모든 수신 엣지들의 시그모이드의 합을 나눈 것으로 얻어지는 정규화된 시그모이드이다. 주의해야 할 건, 게이트 항을 계산하기 위해서는 다음과 같이 계산되는 엣지 $\boldsymbol{e_{j}}$의 표현이 필요하다:

은닉 엣지 표현 $\boldsymbol{e_{j}^{h}}$는 초기 엣지 표현 $\boldsymbol{e_{j}^{x}}$와 $\texttt{ReLU}(\cdot)$ 가 적용된 $\boldsymbol{e_{j}}$의 합이다. 여기서 $\boldsymbol{e_{j}}$는 $\boldsymbol{e_{j}^{x}}$, 정점 $v_{j}$의 입력 표현 $\boldsymbol{e_{j}^{x}}$, 그리고 정점 $v$의 입력 표현 $\boldsymbol{x}$에 각 회전이 적용되진 값들의 합에서 주어진다.

참고: 밑에 은닉 표현 (e.g.* $2^\text{nd}$ 레이어의 은닉 표현)을 계산하기 위해, 위 방정식에서의 입력 특징 표현을 $1^\text{st}$ 레이어 특징 표현으로 바꾸는 것이 가능하다.*

그래프 분류와 Residual Gated GCN 레이어

이번 섹션에서는, 그래프 분류 문제와 Residual Gated GCN 레이어의 코드에 대해 알아볼 것이다. import 문과 더불어 다음 코드들을 더한다:

os.environ['DGLBACKEND'] = 'pytorch'
import dgl
from dgl import DGLGraph
from dgl.data import MiniGCDataset
import networkx as nx

첫줄은 DGL에 백엔드에 PyTorch를 사용하라 명령한다.

Deep Graph Library (DGL)는 그래프에 관해 다양한 기능들을 제공하고, networkx는 그래프의 시각화를 도와준다.

이 노트북에서의 목표는 주어진 그래프의 구조를 8가지의 그래프 타입중 하나로 분류하는 것이다. 데이터셋은 dgl.data.MiniGCDataset에서 주어지며 그래프의 숫자(num_graphs) 를 min_num_v와 max_num_v사이의 노드들을 보여준다. 따라서 얻은 모든 그래프들은 서로 같은 수의 노드과 엣지를 갖지 않는다.

참고: DGLGraphs에 익숙해지기 위해서 짧은 튜토리얼을 참조하는 것을 추천한다 참조.

그래프를 만든 후 다음 작업은 도메인에 신호를 추가하는 것이다. 특징들은DGLGraph의 노드와 엣지에 적용될 수 있다. 특징들은 이름 (문자열)과 텐서 (필드)의 딕셔너리로 표현된다. ndata과 edata는 모든 노드과 엣지들의 특징 데이터를 접근하기 위한 문법적 설탕^{syntax sugar}이다.

아래의 코드는 특징들이 어떻게 생성되는지 보여준다. 각 노드는 부속 엣지 수와 동일한 값이 할당되고 각 엣지는 1이 할당됩니다.

def create_artificial_features(dataset):
    for (graph, _) in dataset:
        graph.ndata['feat'] = graph.in_degrees().view(-1, 1).float()
        graph.edata['feat'] = torch.ones(graph.number_of_edges(), 1)
    return dataset

아래와 같이 학습 데이터와 테스트 데이터는 생성되고 특징은 할당된다:

trainset = MiniGCDataset(350, 10, 20)
testset = MiniGCDataset(100, 10, 20)

trainset = create_artificial_features(trainset)
testset = create_artificial_features(testset)

테스트 데이터에서의 샘플 그래프는 다음과 같은 표현을 갖는다. 여기서 그래프가 15개의 노드와 45개의 엣지를 갖고 노드과 엣지 모두 예상대로 (1,)모양의 특징 표현을 갖는 것을 확인할 수 있다. 또한, 0 은 이 그래프가 클래스 0에 속함을 의미한다.

(DGLGraph(num_nodes=15, num_edges=45,
         ndata_schemes={'feat': Scheme(shape=(1,), dtype=torch.float32)}
         edata_schemes={'feat': Scheme(shape=(1,), dtype=torch.float32)}), 0)

DGL 메시지와 Reduce 함수

DGL에서는 message functions 는 엣지 UDF (사용자 정의 함수)로 표현된다. 엣지 UDF는 단일 인수 edges를 받고 소스 노드 특징, 목적지 노드 특징, 그리고 엣지 특징에 각각 액세스 하기 위한 3개의 멤버 src, dst, data 가 있다.

reduce function 은 노드 UDF 이고 노드 UDF에는 data 와 mailbox 두 개의 멤버가 있는 단일 인수^{single argument} nodes가 있다. data에는 노드 특징을 갖고 mailbox는 두 번째 차원을 따라 쌓인 모든 수신 메시지 특징을 갖는다 (그래서 dim=1 인수를 갖는다).

update_all(message_func, reduce_func)는 모든 엣지들에 메세지를 보내고 모든 노드들을 업데이트한다.

Gated Residual GCN 레이어 구현

Gated Residual GCN 레이어는 아래 코드 처럼 구현된다.

먼저, 입력 특징 $\boldsymbol{Ax}$, $\boldsymbol{Bx_{j}}$, $\boldsymbol{Ce_{j}^{x}}$, $\boldsymbol{Dx_{j}}$ and $\boldsymbol{Ex}$의 모든 회전은 __init__함수 안의 nn.Linear레이어를 정의함과 forward함수 안의 선형 레이어를 통한 입력 표현 h와 e의 순전파^{forward propagating}로 계산이 가능하다.

class GatedGCN_layer(nn.Module):

    def __init__(self, input_dim, output_dim):
        super().__init__()
        self.A = nn.Linear(input_dim, output_dim)
        self.B = nn.Linear(input_dim, output_dim)
        self.C = nn.Linear(input_dim, output_dim)
        self.D = nn.Linear(input_dim, output_dim)
        self.E = nn.Linear(input_dim, output_dim)
        self.bn_node_h = nn.BatchNorm1d(output_dim)
        self.bn_node_e = nn.BatchNorm1d(output_dim)

그 다음으로는, 엣지 표현을 계산한다. 이는 message_func함수 안에서 이루어지며 모든 엣지에 반복하여 엣지 표현을 계산한다. 특히, e_ij = edges.data['Ce'] + edges.src['Dh'] + edges.dst['Eh'] 라인은 위의 (Eq. 7)를 계산하며, message_func 함수는 Bh_j ((Eq. 5)에서의 $\boldsymbol{Bx_{j}}$) 와 e_ij (Eq. 7) 를 목적 노드의 mailbox에 보낸다.

def message_func(self, edges):
    Bh_j = edges.src['Bh']
    # e_ij = Ce_ij + Dhi + Ehj
    e_ij = edges.data['Ce'] + edges.src['Dh'] + edges.dst['Eh']
    edges.data['e'] = e_ij
    return {'Bh_j' : Bh_j, 'e_ij' : e_ij}

세번째로, reduce_func 함수는 보내진 메시지들을 message_func함수로 모은다. 노드 데이터 Ah와 보내진 데이터 Bh_j 그리고 mailbox에서의 e_ij 를 모은 후, h = Ah_i + torch.sum(sigma_ij * Bh_j, dim=1) / torch.sum(sigma_ij, dim=1) 라인은 (Eq.5) 에서 나타나는 각 노드들의 은닉 표현을 계산한다. 하지만 참고해야할 건, 오직 이는 $\texttt{ReLU}(\cdot)$ 와 잔차 연결을 뺀 $(\boldsymbol{Ax} + \sum_{v_j→v}{\eta(\boldsymbol{e_{j}})\odot \boldsymbol{Bx_{j}}})$ 항만을 표현한다.

def reduce_func(self, nodes):
    Ah_i = nodes.data['Ah']
    Bh_j = nodes.mailbox['Bh_j']
    e = nodes.mailbox['e_ij']
    # sigma_ij = sigmoid(e_ij)
    sigma_ij = torch.sigmoid(e)
    # hi = Ahi + sum_j eta_ij * Bhj
    h = Ah_i + torch.sum(sigma_ij * Bh_j, dim=1) / torch.sum(sigma_ij, dim=1)
    return {'h' : h}

g.update_all을 호출한 forward 함수 안에는 (Eq.5) 에서의 $(\boldsymbol{Ax} + \sum_{v_j→v}{\eta(\boldsymbol{e_{j}})\odot \boldsymbol{Bx_{j}}})$와 (Eq. 7) 에서의 $\boldsymbol{e_{j}}$를 나타내는 그래프 합성곱의 결과 h와 e를 얻는다. 그런 다음 그래프 노드 크기와 그래프 엣지 크기에 대해 각각 h와 e를 정규화하면 배치 정규화가 적용되어 네트워크를 효과적으로 학습시킬 수 있게된다. 마지막으로, forward함수에 의해 반환되는 노드와 엣지에 대한 은닉 표현을 얻기 위해 $\texttt{ReLU}(\cdot)$를 적용하고 잔차 연결을 추가한다.

def forward(self, g, h, e, snorm_n, snorm_e):

    h_in = h # residual connection
    e_in = e # residual connection

    g.ndata['h']  = h
    g.ndata['Ah'] = self.A(h)
    g.ndata['Bh'] = self.B(h)
    g.ndata['Dh'] = self.D(h)
    g.ndata['Eh'] = self.E(h)
    g.edata['e']  = e
    g.edata['Ce'] = self.C(e)

    g.update_all(self.message_func, self.reduce_func)

    h = g.ndata['h'] # result of graph convolution
    e = g.edata['e'] # result of graph convolution

    h = h * snorm_n # normalize activation w.r.t. graph node size
    e = e * snorm_e # normalize activation w.r.t. graph edge size

    h = self.bn_node_h(h) # batch normalization
    e = self.bn_node_e(e) # batch normalization

    h = torch.relu(h) # non-linear activation
    e = torch.relu(e) # non-linear activation

    h = h_in + h # residual connection
    e = e_in + e # residual connection

    return h, e

다음으로 여러개의 완전 연결 레이어 (FCN)을 포함하는MLP_Layer 모듈을 정의하고 완전 연결 레이어들의 리시트를 만들어 네트워크를 따라 전달한다.

마지막으로, 이전에 정의된 클래스 GatedGCN_layer and MLP_layer으로 구성된 GatedGCN를 정의한다. GatedGCN의 정의는 아래와 같다.

 class GatedGCN(nn.Module):
    def __init__(self, input_dim, hidden_dim, output_dim, L):
        super().__init__()
        self.embedding_h = nn.Linear(input_dim, hidden_dim)
        self.embedding_e = nn.Linear(1, hidden_dim)
        self.GatedGCN_layers = nn.ModuleList([
            GatedGCN_layer(hidden_dim, hidden_dim) for _ in range(L)
        ])
        self.MLP_layer = MLP_layer(hidden_dim, output_dim)
    def forward(self, g, h, e, snorm_n, snorm_e):
        # input embedding
        h = self.embedding_h(h)
        e = self.embedding_e(e)
        # graph convnet layers
        for GGCN_layer in self.GatedGCN_layers:
            h, e = GGCN_layer(g, h, e, snorm_n, snorm_e)
        # MLP classifier
        g.ndata['h'] = h
        y = dgl.mean_nodes(g,'h')
        y = self.MLP_layer(y)
        return y

생성자^constructor 안에서 전에 정의된 모델 GatedGCN_layer와 self.MLP_layer의 ($L$크기를 가진) 리시트인 e와h (self.embedding_e and self.embedding_h)의 임베딩을 정의한다. 그 다음, 이러한 초기화를 사용하여 모델을 진행하고 y를 출력한다.

# instantiate network
model = GatedGCN(input_dim=1, hidden_dim=100, output_dim=8, L=2)
print(model)

모델의 주요 구조는 다음과 같다:

GatedGCN(
  (embedding_h): Linear(in_features=1, out_features=100, bias=True)
  (embedding_e): Linear(in_features=1, out_features=100, bias=True)
  (GatedGCN_layers): ModuleList(
    (0): GatedGCN_layer(...)
    (1): GatedGCN_layer(... ))
  (MLP_layer): MLP_layer(
    (FC_layers): ModuleList(...))

당연하게도 (L=2 이므로) 두개의 GatedGCN_layer 레이어와 MLP_layer 가 있으며 최종적으로 8개의 값을 출력한다.

나아가 train과 evaluate함수를 정의하고 train 함수에서는 dataloader 에서 샘플을 가져오는 제네릭 코드^{generic code}를 가지며, batch_graphs, batch_x, batch_e, batch_snorm_n, batch_snorm_e는 모델에 입력되어 (크기 8의) batch_scores을 출력하며 예측된 점수들은 손실함수의 실측 값 과 비교된다: loss(batch_scores, batch_labels). 그 다음으로 경사도를 영처리(optimizer.zero_grad()), 를 하며 역전파 (J.backward())와 가중치를 업데이트(optimizer.step())한다. 마지막으로, 에폭^epoch과 학습 정확도의 손실이 계산되며, 이는 evaluate에서 또한 비슷한 코드를 사용한다.

드디어 학습할 모든 준비를 마쳤다! 40 에폭의 학습의 결과, 모델은 $87$%의 그래프 분류 정확도를 가졌다.