그래프 합성곱 신경망 II

스펙트럼 그래프 합성곱 신경망^{Spectral Graph ConvNets} (GCNs)

지난 섹션에서는, 그래프 합성곱 신경망을 정의하는 두 가지 방법 중 하나인 그래프 스펙트럼 이론에 대해 살펴봤었고, 이번 섹션에서는 그래프 스펙트럼 이론을 이용해 스펙트럼 GCNs를 정의할 것이다.

기본 스펙트럼 GCN ^{Vanilla Spectral GCN}

그래프 스펙트럼 합성곱 신경망의 정의는 다음과 같다: 주어진 레이어 $h^l$에 다음 레이어의 활성화 함수^activation는

$\eta$는 비선형 활성화 함수^{nonlinear activation}를 뜻하고 $w^l$은 공간 필터^{spatial filter}이다. 우측 수식은 $\eta(\hat{w}^l(\Delta)h^l)$와 같으며 $\hat{w}^l$는 스펙트럼 필터를 뜻하고 $\Delta$는 라플라시안^Laplacian이다. 우측 공식은 $\eta(\boldsymbol{\phi} \hat{w}^l(\Lambda)\boldsymbol{\phi^\top} h^l)$으로 좀 더 분해^decompose할 수 있으며, $\boldsymbol{\phi}$는 푸리에 행렬^{Fourier matrix}이고, $\Lambda$ 는 고유값^eigenvalues이다. 이는 최종적으로 아래의 활성화 함수를 도출한다.

목표는 스펙트럼 필터 학습을 일일이 하는 것이 아닌 역전파^{backpropagation}를 이용해 학습시키는 것이다.

이 기법은 합성곱 신경망에 사용된 최초의 스펙트럼 기법이지만 몇몇가지의 제약점들이 존재한다:

• 필터의 공간 국소화^{spatial localization of filters}가 보장되지 않음
• 각 레이어 별로 $O(n)$ 변수^parameters를 학습시켜야함 ($\hat{w}(\lambda_1)$ 에서$\hat{w}(\lambda_n)$ 까지)
• $\boldsymbol{\phi}$가 조밀 행렬^{dense matrix}이기에 학습 속도가 $O(n^2$)

SplineGCNs

SplineGCNs는 국소 공간 필터^{localized spatial filters}를 얻기 위해 매끄러운^smooth 스팩트럼 필터를 이용한다. 주파수 영역^{frequency domain}의 매끄러움과 공간의 국소화의 연결은 파르스발 항정식 ^{Parseval’s Identity}(하이젠베르크 불확정성 원리^{Heisenberg uncertainty principle} 포함)에 기반을 두고있다: 작은 스펙트럼 필터의 미분^derivative (더 매끄러운 함수일 수록) $\Leftrightarrow$ 작은 공간 필터 (국소화)의 분산^variance

어떻게해야 매끄러운 스펙트럼 필터를 얻을 수 있을까? 이는 스펙트럼 필터를 $K$ 매끄러운 커널 $\boldsymbol{B}$ (스플라인^splines)의 일차 결합^{linear combination}으로 분해하여 다음과 같게 만든다 $\hat{w}^l(\Lambda)=diag(\boldsymbol{B}w^l)$. 활성화 공식은 다음과 같다:

이제 역전파로 학습될 각 레이어 별로 $O(1)$의 매개변수를 갖지만 학습 복잡도가 아직 $O(n^2)$으로 남는다는 문제가 있다.

LapGCNs

어떻게 하면 (그래프 사이즈 $n$에 비례하여) 선형 시간 $O(n)$로 학습이 가능할까? 이는 $O(n^2)$ 복잡도는 라플라시안 고유벡터를 사용해 나온 직접적인 결과이기에 고유분해법이 아닌 라플라시안 함수의 직접적인 학습을 통해 해결 가능하다. 스펙트럼 함수는 다음과 같이 라플라시안의 단항^monomial이다.

매력적인 특징 중 하나는 필터가 정확히 k-hop 근방 안에 위치한다는 것이다.

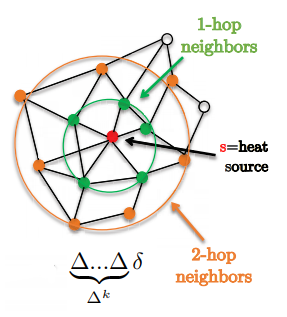
Figure 1: 1-hop과 2-hop 근방을 나타낸다.

$\Delta^kh$를 다음과 같이 정의된 재귀함수^{recursive equation} $X_k$로 표현한다:

희소 그래프^{sparse graphs}에서의 복잡도는 이제 $O(E.K)=O(n)$이고, 선형연산을 위해 $X_k$를 $\bar{X}$로 재배열^reshape이 가능하여 다음과 같은 활성화 함수를 갖는다:

주의: 사실 라플라시안 고유분해를 사용하지 않았고, 모든 연산법은 (스펙트럼이 아닌) 공간적 영역^{spatial domain}에서 이뤄지기에, 스펙트럼 GCNs 이라고 부르는 것은 잘못된 표현법이다. 더 나아가, LapGCNs의 또 다른 단점은 합성곱 신경망이 희소 선형 연산^{sparse linear operations}을 이용해, GPU에 최적화 되어있지 않다는 점이다.

국소 필터, 각 레이어 별 $O(1)$의 매개변수, $O(n)$ 학습복잡도를 통해 일반적인 GCNs의 한계점들을 해결하였지만 LapGCNs의 사용된 단항식 기저^{monomial basis} 는 직교^orthogonal가 아니기에 아직 최적화에 불안정하다는 단점이 존재한다 (하나의 계수^coefficient를 바꿈으로 함수 근사^{function approximation}를 바꾼다).

ChebNets

불안정 기저 문제를 해결하기 위해서 직교 기저들을 사용 가능하지만 선형 복잡도를 위해서는 반드시 재귀함수가 필요하다는 조건이 있다. ChebNets의 경우 체비쇼프 다항식 ^{Chebyshev polynomials}을 이용하며 LapGCN때 처럼 $T_k(\Delta)h$를 다음과 같이 정의되는 재귀함수 $X_k$로 표현한다:

이제 계수 섭동^{coefficient perturbation}에서의 안정성을 확보하였다.

ChebNets는 어떠한 임의의 그래프 정의역에도 사용이 가능한 GCNs이지만, ChebNets은 등방성^isotropic이라는 단점이 존재한다. 일반적인 합성곱 신경망은 유클리드 그리드^{Euclidean grids}가 방향성을 가지기에 이방성 ^anisotropic 필터를 생산해 내지만 스펙트럼 GCNs는 그래프가 방향(상하, 좌우)의 개념이 존재하지 않아 등방성 필터를 계산해 낸다.

이제 2D 스펙트럼 필터를 이용해 ChebNets을 다중 그래프에 적용이 가능하다. 이는, 한 예로, 영화 그래프와 관객 그래프를 이용한 추천 시스템에는 유용할 수 있다. 다중 그래프 ChebNets는 다음과 같은 활성화 함수를 갖는다:

CayleyNets

ChebNets은 관심 주파대^{frequency bands of interest} (그래프 군집^{graph communities})로 필터를 제공(국소화^localize)하기에는 불안정하다. CayleyNets에서는 대신에 정규 직교 기저를 케일리 유리수^{Cayley rationals}로 사용한다.

CayleyNets은 ChebNets과 (둘 다 등방성이라는) 같은 성질들을 갖지만 , CayleyNets은 주파수^frequency에 위치하며, 좀 더 높은 단계의 필터를 제공한다.

공간 그래프 합성곱 신경망 Spatial Graph ConvNets

템플릿 매칭

공간 그래프 합성망을 이해하기 위해서는, 합성곱 신경망의 템플릿 매칭의 정의를 되짚어야 한다.

그래프에 템플릿 매칭을 할 때 가장 큰 문제점은 템플릿에 꼭짓점의 순서나 위치가 명확하지 않다는 점이며, 가진거라곤 정보를 매칭하기에 부족한 꼭짓점의 인색^indices뿐이다. 어떻게 구성해야 템플릿 매칭이 꼭짓점 재매개화^{reparametrisation}에 불변할 수 있을까? 다시 말해, 만약 그래프의 꼭짓점 하나가 임의의 인색 6을 가지고 있다고 한다면, 이 인색은 122 또한 될 수 있다. 그러므로 꼭짓점들의 인색에 독립된 템플릿 매칭을 할 수 있어야한다.

가장 간단한 방법은 템플릿 벡터를 $w_{j1}$,$w_{j2}$, $w_{j3}$, 등등의 여러개 말고 $w^l$로 딱 하나만 갖는 것이다. 그래서 벡터 $w^l$를 그래프의 다른 특징^features들과 매칭하는 것이며 오늘 날 그래프 신경망들은 이러한 성질을 이용한다.

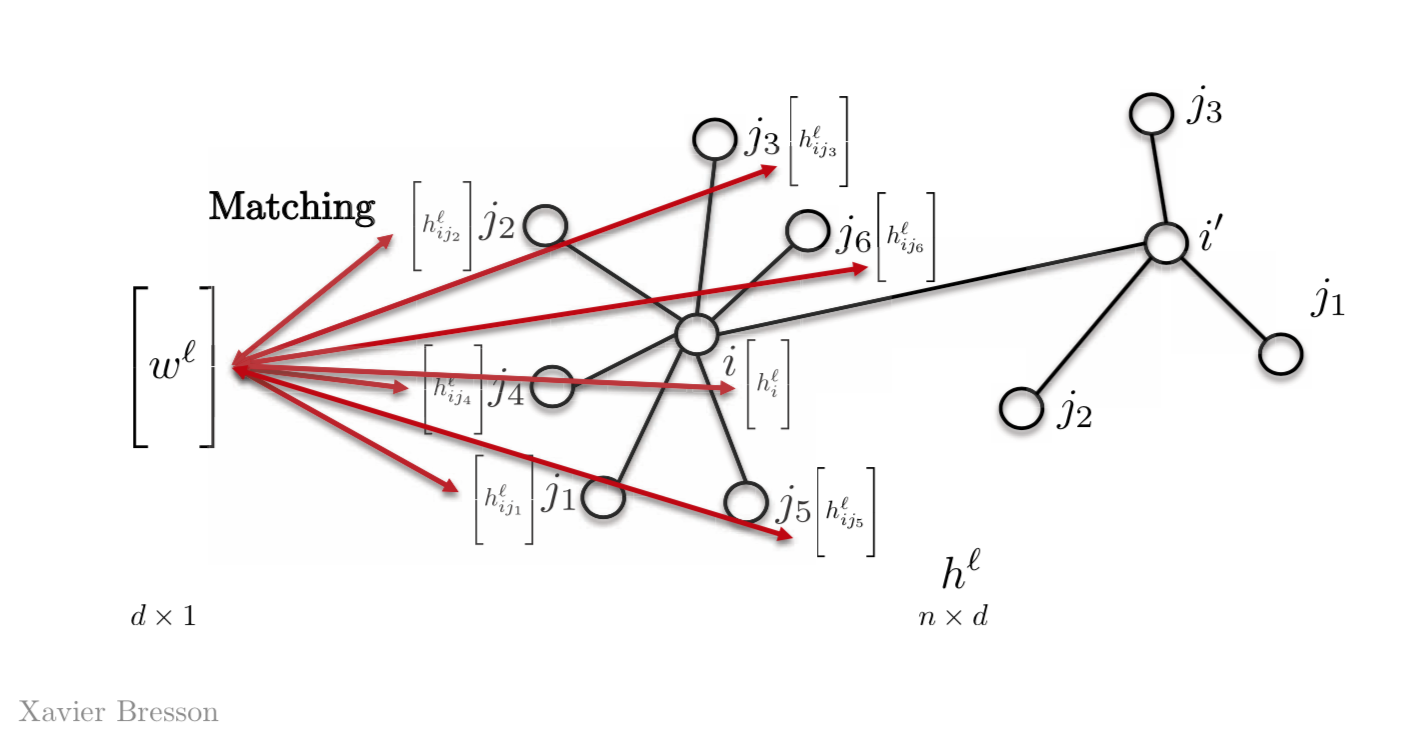
Figure 2: Template Matching using a template vector

수학적으로 하나의 특징에 대하여,

$w^l$ 는 레이어 $l$에서의 $d \times 1$ 차원을 가진 템플릿 벡터이다. $h_{ij}^l$는 꼭짓점 $j$의 $d \times 1$ 차원을 가진 벡터이며, 꼭짓점 $i$에서의 스칼라 량^{scalr quantity} $h_{i}^{l+1}$를 갖게한다.

더 많은 ($d$)특징들에 대해서는,

$\boldsymbol{W}^l$는 $d \times d$ 차원수를 가지며, $h_{i}^{l+1}$의 차원수는 $d \times 1$이다.

벡터적 표현으로는,

$\boldsymbol{A}$는 $n \times n$ 차원을 가진 인접행렬^{adjacency matrix}이고, $h^l$은 레이어 $I$에 $n \times d$ 차원을 가진 활성화 함수이다.

등방성 GCNs ^{Isotropic GCNs}

기본적인 공간 ^{GCNs Vanilla Spatial GCNs}

전에 사용된 정의와는 같지만, 이웃점들의 평균값^{mean value}들을 찾는것 과 같은 방식으로 대각행렬^{Diagonal matrix}을 공식에 추가하였다.

행렬 표현으로는,

$\boldsymbol{A}$ 는 $n \times n$ 차원을 가지고, $h^{l}$는 $n \times d$ 차원을, 그리고 $W^{l}$은 $d \times d$ 차원을 가지고 $n \times d$차원의 $h^{l+1}$를 가진다.

그리고 벡터적 표현으로는,

$h_{i}^{l+1}$는 $d \times 1$차원을 갖는다.

벡터적 표현은 꼭짓점 재매개화에 불변^invariant하며 꼭짓점 순서의 부재를 처리한다. 저번 예제에 추가로 설명을 더하자면, 만약 꼭짓점의 번호가 6에서 122로 바뀌어도 다음 레이어 $h^{l+1}$의 활성화 함수 계산에 전혀 지장이 없다는 것이다.

이로인해 이웃점들 끼리의 서로 다른 크기 문제들도 해결할 수 있으며, 다시 말해 이는 인근점들이 4개 든 10개든 계산이 달라지지 않는다는 것이다.

국부 수용영역^{local reception field}은 디자인에 의해 주어지며, 즉 이는 그래프 신경망에서는 이웃점들만 고려하면 된다는 것이다.

우린 가중치 공유^{weight sharing}를 사용할 수 있고, 이는 합성곱의 성질인 모든 특징에 그래프의 위치에 상관없이 같은 $\boldsymbol{W}^{l}$행렬을 갖는다는 뜻이다.

이 공식은 모든 작업이 로컬로 이루어지기 때문에 그래프 사이즈에도 독립되어 있다.

이는 등방성 모델이라 인근점들 또한 $\boldsymbol{W}^{l}$ 행렬을 갖는다.

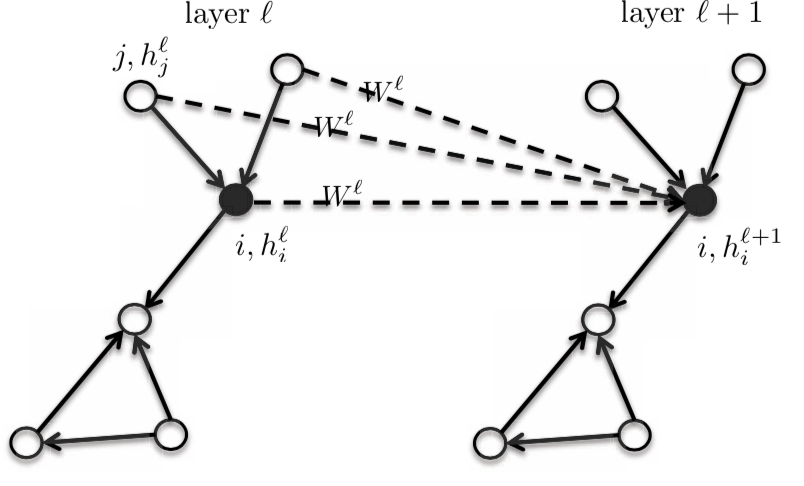
Figure 3: Isotropic model

그래서 다음 레이어 $h_{i}^{l+1}$ 의 활성화 함수는 꼭짓점 $i$와 $i$의 인근점들의 전 레이어 $h_{i}^{l}$의 활성화 함수이다.

ChebNets와 기본 공간 GCNs

위와 같이 정의된 기본 공간 GCN은 ChebNets의 단순화된 버전이다. 처음 두 체비쇼프 함수를 이용해 ChebNets의 확장^expansion을 줄일 수 있으며 다음과 같은 모습을 띄게 된다,

GraphSAGE (SAmple aggreGatE)

만약 기본 공간 GCN에서의 간선^edges들이 각 인접행렬 $\boldsymbol{A}_{ij} = 1$의 형태로 주어진다면, 아래와 같은 수식을 얻게된다,

이 공식에는 중심/핵심 정점 ^{central/core vertex} $i$와 $i$의 인근점들에게 같은 템플릿 가중치 $\boldsymbol{W}^{l}$를 부여한다. 이는 중심 정점을$\boldsymbol{W}{1}^{l}$로 하고, 원-핫^one-hot 인근점에는 $\boldsymbol{W}{2}^{l}$의 다른 템플릿 꼭짓점을 부여함으로 둘을 구분지을 수 있다. 위와 같은 작업은 GNN의 성능을 상당히 향상시키며 인근점들이 모두 같은 가중치를 가졌기에 이 모델은 사실상 등방성 모델로 간주된다.

$\boldsymbol{W}{1}^{l}$ 과 $\boldsymbol{W}{2}^{l}$는 $d \times d$ 차원을 갖는다; $h_{i}^{l}$과 $h_{j}^{l}$는 $d \times 1$ 차원을 갖는다.

이 방정식에서는, 평균값이 아닌 $\boldsymbol{W}{2}^{l} h{j}^{l}$의 합계^summation 또는 최댓값^maximum이나, $h_{j}^{l}$의 LSTM을 찾아 볼 수 있다.

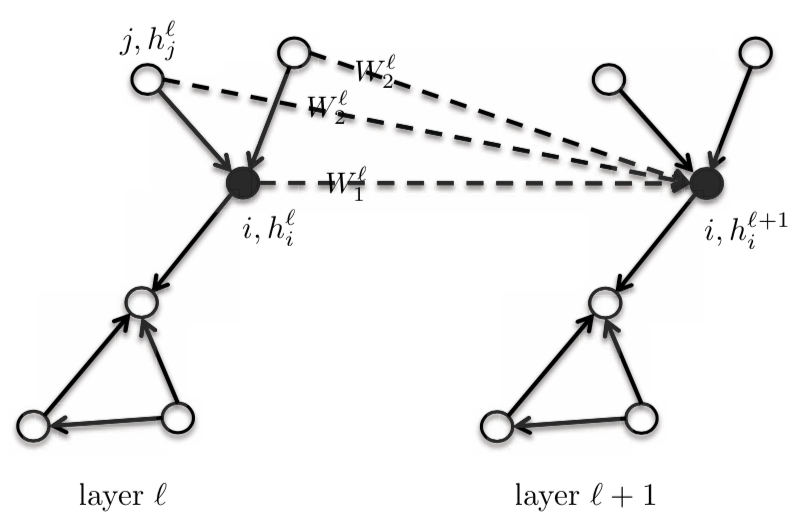
Figure 4: GraphSAGE

그래프 동형 사상 네트워크^{Graph Isomorphism Networks (GIN)}

동형^isomorphic이 아닌 그래프를 구분할 수 있는 구조. 동형 사상 ^Isomorphism은 그래프간 닮음에 대한 척도이다. 아래의 그림에서 보여지는 것 처럼, 두 그래프는 서로 동형이다. 동형 그래프는 서로 비슷하게 취급되며, 비동형^{non-isomorphic} 그래프들은 서로 다르게 취급된다.

GIN은 동형 GCN이다.

여기서 $\texttt{BN}$은 배치정규화^{Batch Normalization}를 뜻한다.

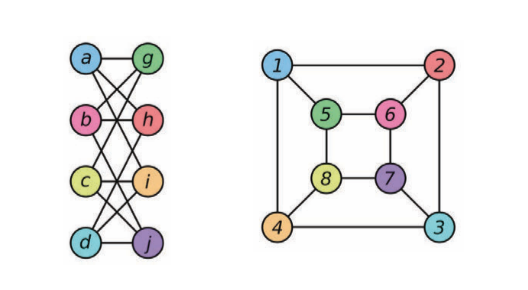
Figure 5: 두 동형 사상 그래프의 예제

비등방성 GCNs ^{Anisotropic GCNs}

방향성 구조는 상하좌우 방향에 기초를 두기 때문에 기본적인 CNN은 (특정 방향을 향하는) 비등방성 필터를 만들 수 있다. 하지만 위에서 언급했듯이, GCNs에는 방향의 개념이 없기에 등방성 필터만 만들 수 있다. 비등방성은 간단히 간선 특징으로 설명이 가능한데, 분자^molecule가 단일^single, 이중^double 또는 삼중 결합^{triple bond}이 될 수 있는 것을 예로 들 수 있다. 그래프에서는 이를 각 이웃점들의 가중치를 다르게 함으로 구현이 가능하다.

MoNets

MoNets은 그래프의 차수^degree를 이용해 가우시안 혼합 모델^{Gaussian Mixture Model (GMM)}의 매개변수를 학습한다.

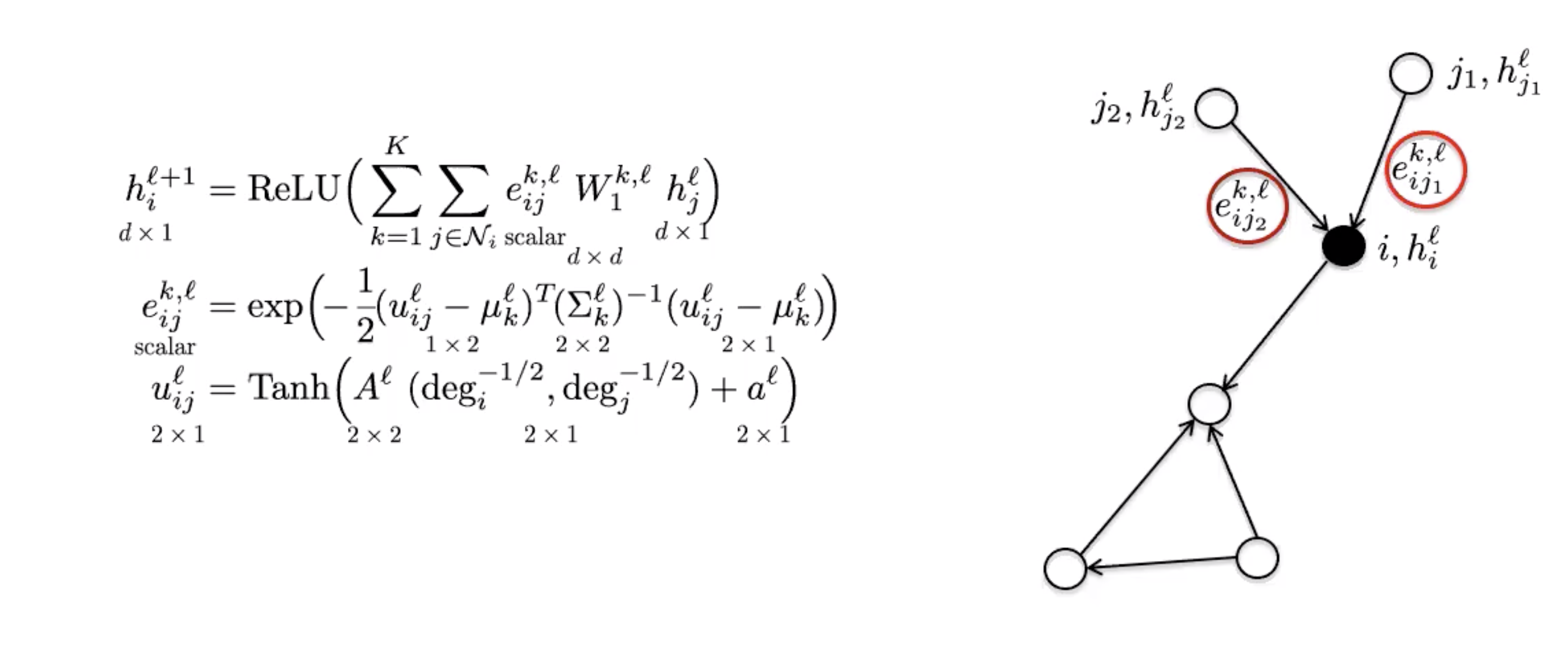
Figure 6: MoNet

그래프 어텐션 네트워크 Graph Attention Networks (GAT)

GAT는 어텐션 메커니즘을 사용해 이웃 집계 함수^{neighbourhood aggregation function}의 비등성을 소개한다.

Figure 7: GAT

Gated Graph ConvNets

Gated Graph ConvNets는 GAT에서 사용된 희소 어텐션 메커니즘^{sparse attention mechanis} 처럼 소프트 어텐션 과정^{softer attention process}으로 보여질 수 있는 간단한 간선 게이트 메커니즘^{simple edge gating mechanism}을 이용한다.

Figure 8: Gated Graph ConvNet

그래프 트랜스포머 Graph Transformers

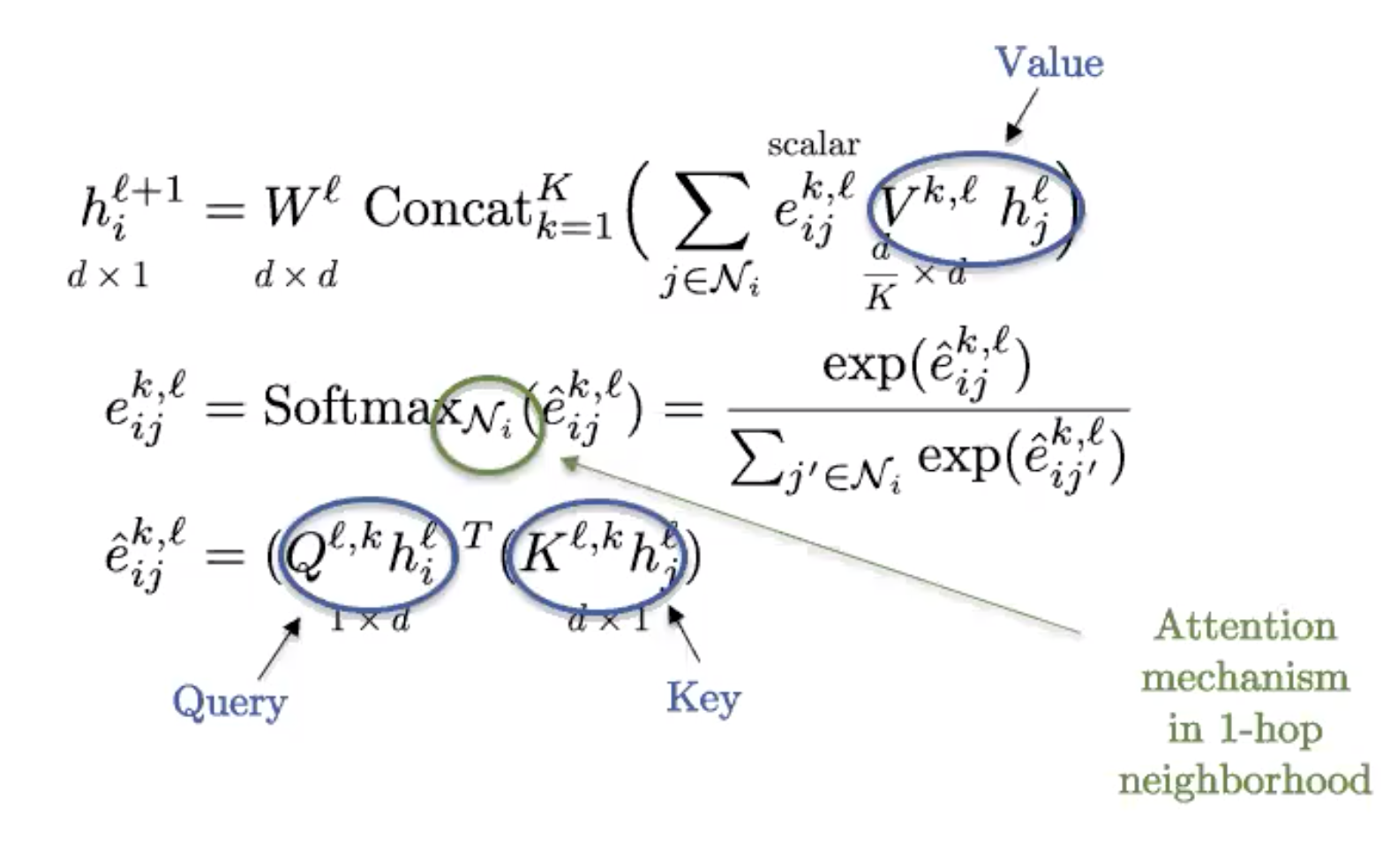
Figure 9: Graph Transformer

그래프 트랜스포머는 NLP에서 널리 쓰이는 기본적인 트랜스포머의 그래프 버전이다. 만약 그래프가 완전히 연결^{fully connected}되있다면 (모든 꼭지점이 서로 연결되있는 것), 기본 트랜스포머의 정의를 다시 사용할 수 있다.

그래프는 희소성으로부터 구조를 얻기에 완전 연결 그래프는 잠여한^trivial 구조를 가지고 본질적으로는 집합^set이다. 트랜스포머는 집합 신경망으로 볼 수 있고, 실제로 특징들의 집합/묶음^sets/bags을 분석하는데 최고의 기법이다.

GNNs 벤치마킹^benchmarking

벤치마킹은 어느 분야에서든 매우 중요한 과정이다. 최근 출시된 벤치마크 Benchmarking Graph Neural Networks 는 4개의 핵심 그래프 문제- 그래프 분류^{classification}, 그래프 회귀^regression, 꼭짓점 분류, 간선 분류 - 를 풀기 위한 6개의 중간 규모 데이터셋을 제공한다. 데이터들의 규모가 중간 정도이지만, 여러 GNN의 통계적으로 다른 트렌드들을 분석하기에는 충분하다.

그래프 회귀 작업의 한 예로, 분자의 용해도^{molecular solubility}를 예측을 들 수 있다.

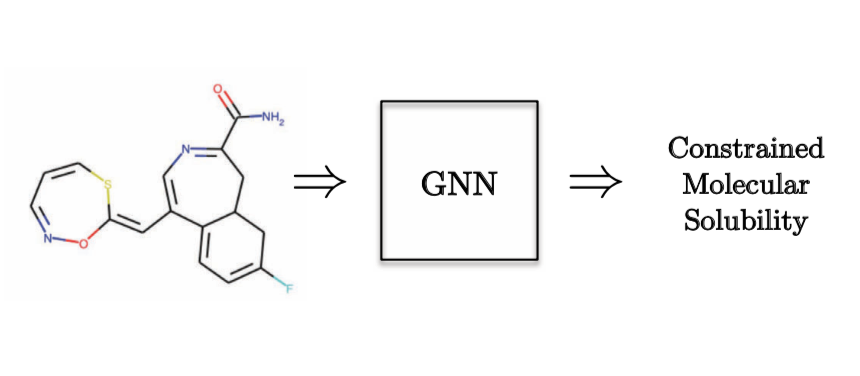
Figure 10: 그래프 회귀 작업 - 양자화학

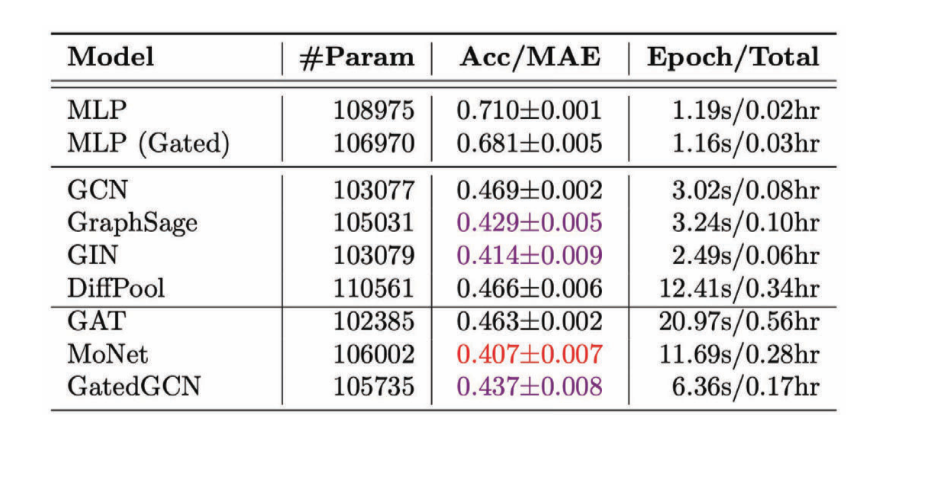
Figure 11: 여러 GCN들의 회귀 작업 성과

비등방성 GCN은 방향성 특성을 사용하기에 대부분의 경우 비등방성 GCN이 등방성 GCN 보다 더 나은 결과를 가지는 것을 확인할 수 있다.

그래프 분류 작업의 경우, 컴퓨터 비전 문제는 사진의 슈퍼노드^{super nodes}의 위치와 사진에 어떤 것을 분류하고 싶은지에 따라 선별된다.

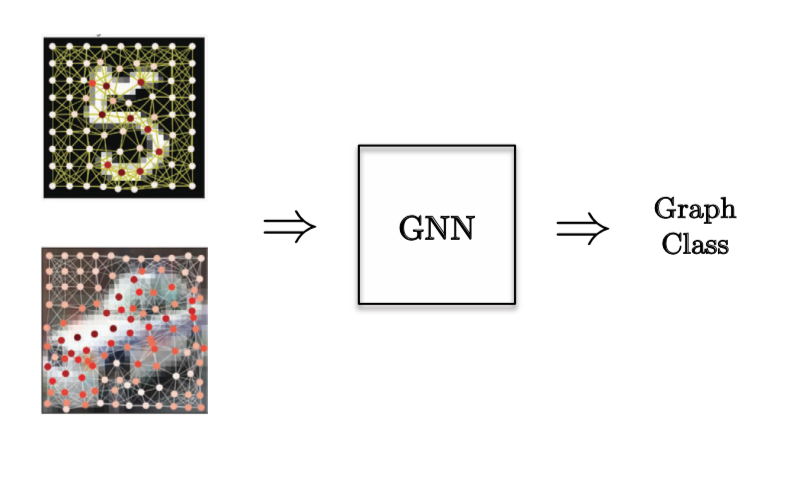
Figure 12: 그래프 분류 작업

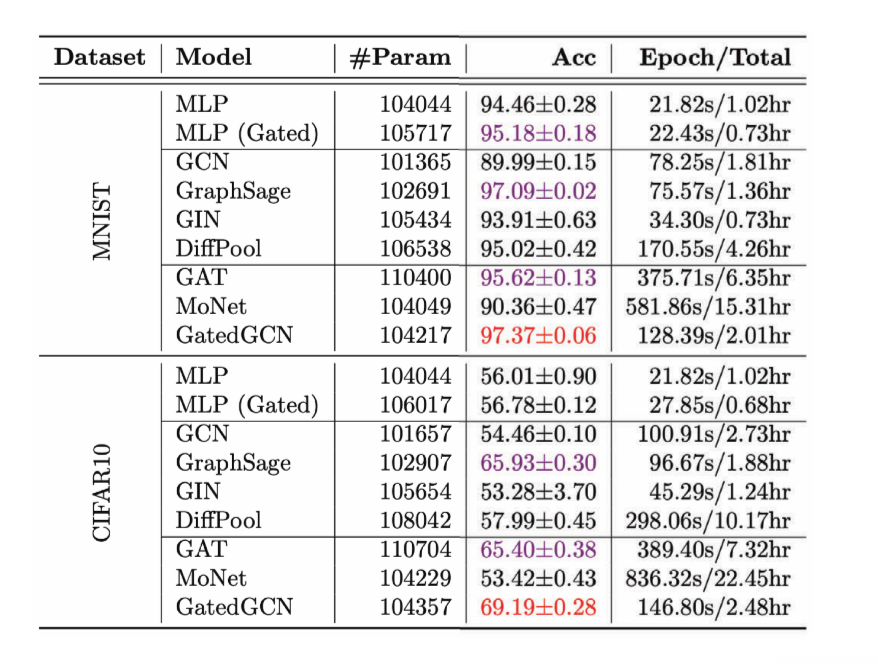
Figure 13: 여러 GCN들의 분류 작업 성과

간선 분류 작업의 경우, 외판원 문제 ^{Travelling Salesman Problem TSP}의 조합 최적화^{Combinatorial Optimization} 문제를 다룬다 - 특정 간선이 최적의 해답에 있는지 확인한다. 만약 간선이 해답에 위치한다면 class 1에, 나머지는 class 0이 된다. 명확한 간선 특징이 필요하며 이러한 작업을 잘 다루는 단 하나의 모델은 GatedGCN이다.

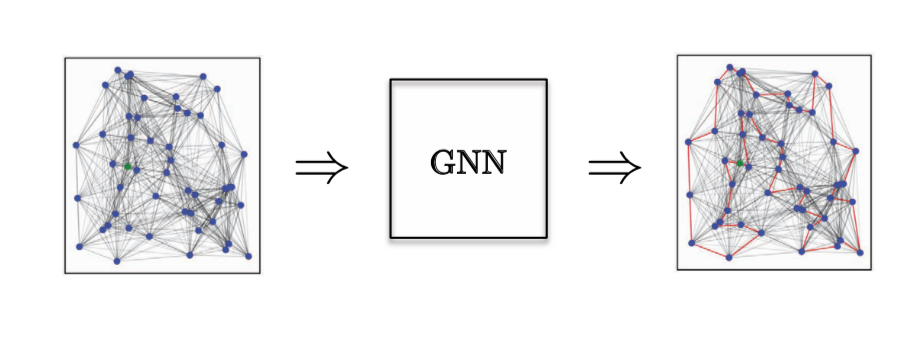
Figure 14: 간선 분류 작업

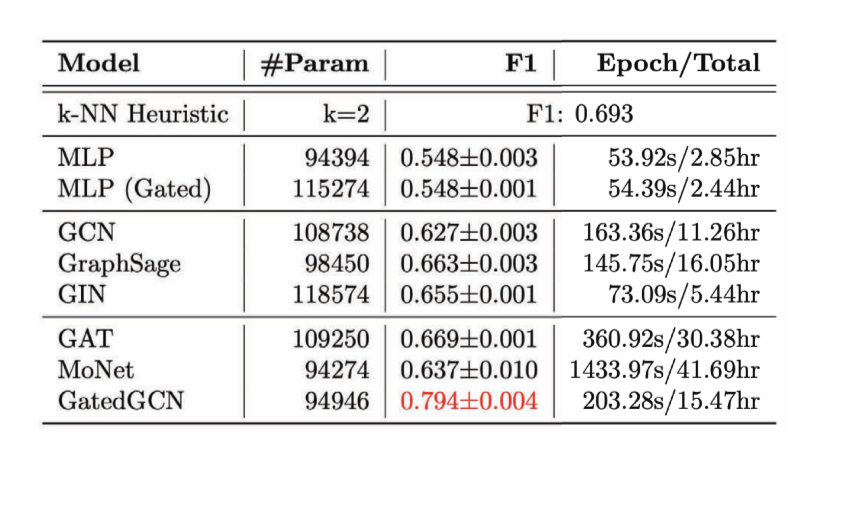
Figure 15: 여러 GCN의 간선 분류 작업의 성과

GCN은 지도 학습 모델^supervised에만 국한되지 않고 자가 지도 작업^{self-supervised}에 또한 사용이 가능하다. 얀 르쿤 박사에 따르면, 거의 모든 자가 지도 학습 작업은 그래프 구조를 띄고있다고 한다. 단어 시퀀스^{sequence of words}를 가지고 빠진 단어나 새로운 문장을 만드는 예측 모델을 만드는 텍스트에서의 자가 지도 학습 작업을 할 때에도 다른 단어와의 일정 거리에서 특정 단어의 빈도와 같은 그래프 구조가 존재한다. 텍스트는 선형 그래프이며 선택된 이웃들은 트랜스포머를 학습하는데 사용될 것이다. 대조학습^{contrastive training}의 경우, 두 점은 비슷하다면 연결되고 같지 않다면 연결이 되지 않는 유사도 그래프^{similarity graph}이다.

결론

GCN은 CNN을 그래프의 데이터로 일반화^generalize하고, 합성곱 연산은 그래프에 맞춰 재정립되어야한다. 템플릿 매칭을 위한 이 방식은 공간 GCN을 소개하며, 스펙트럼 합성곱은 스펙트럼 GCN으로 이어진다.

희소 그래프는 복잡도도 선형이고 GPU에도 사용이 가능하지만, GPU에는 아직 희소 행렬 곱셈이 아직 최적화가 이루어지지 않았다. GCN는 아래처럼 다양한 방면에서 응용되어진다.

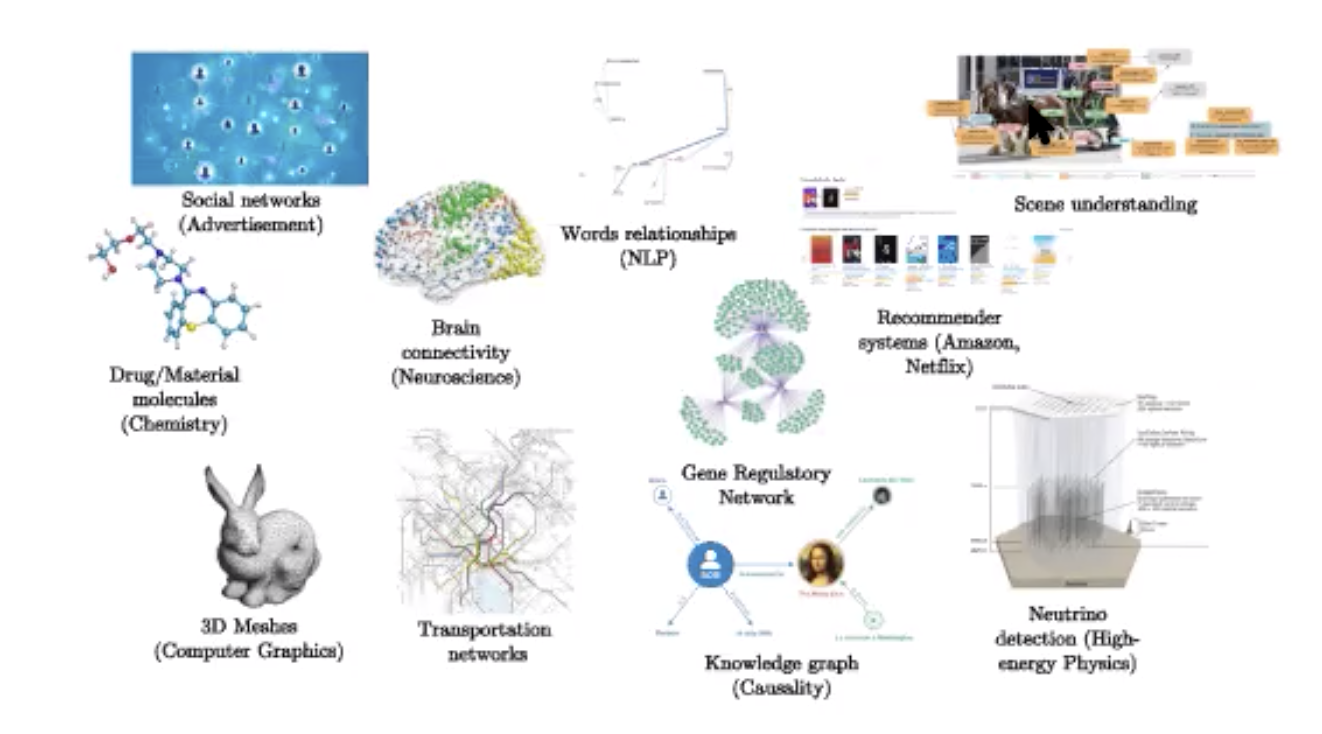
Figure 16: 응용