그래프 합성곱 신경망 I

🎙️ Xavier Bresson

전통적인 합성곱 신경망^{Traditional ConvNets}

합성곱 신경망은 고차원 학습 문제에 매우 효과적인 구조이다.

차원의 저주란?

1024 x 1024 픽셀을 가진 이미지는 1,000,000 차원 공간의 한 점으로 생각될 수 있다. 차원별로 10개의 샘플들을 사용한다면 ${10}^{1,000,000}$ 라는 엄청난 수의 이미지들을 생성한다. 합성곱 신경망은 다음 예제에서 보여지는 것과 같이 고차원 이미지 데이터 최적의 표현을 추출하는 데 매우 효과적이다.

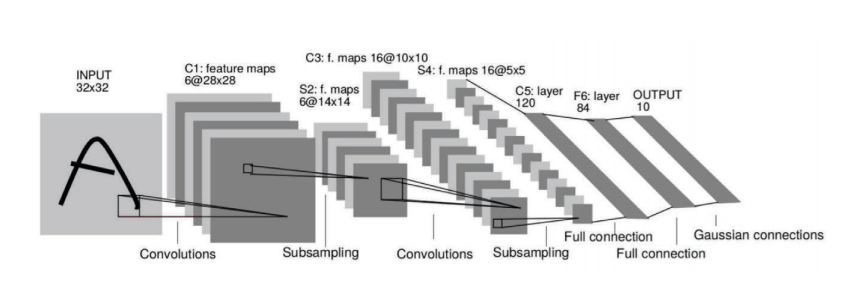
Fig. 1: 합성곱 신경망은 고차원 이미지 데이터에서 표현을 추출한다.

합성곱 신경망의 주요 가정:

1. 데이터(이미지, 비디오, 음성)는 구성적^{compositional}이다.

데이터는 다음과 같은 패턴들을 가진다:

• 집약적^Local 신경망에서의 뉴런은 신경망 전체의 계층이 아닌 오직 인접한 계층들하고만 연결되어있다. 이를 집약적 수용영역 가정^{local reception field assumption}이라고 부른다.
• 정상적^Stationary 비슷한 패턴들을 가지며 이미지 영역^{image domain}에 걸쳐 공유한다. 예로 figure 2에서의 중간 이미지의 노란 침대 시트를 들 수 있다.
• 계층적^Hierarchical 저레벨 특징^feature들은 모여서 중간레벨 특징을 이루고, 이 중간레벨 특징들이 계속해서 모여 더욱더 높은 레벨의 특징들을 이룬다. 예로 시각표현을 들 수 있다. <!–

Fig. 2: Data is compositional.

–>

Fig. 2: 데이터는 구성적이다.

2. 합성곱은 구성적 구조를 활용한다.

합성곱은 합성적 특징들을 추출하여 분류기^classifier나 추천기^recommender 등에 피드^feed한다.

Fig. 3: 합성곱은 합성성 구조에 영향을 끼친다.

그래프 정의역 ^Domain

데이터 정의역

• 이미지, 부피, 비디오는 각각 2D, 3D, 2D + 1 유클리드 정의역^{Euclidean domains}에 펼쳐져 있으며, 각 픽셀은 빨강, 초록, 파랑값의 벡터에 의해 표현된다.

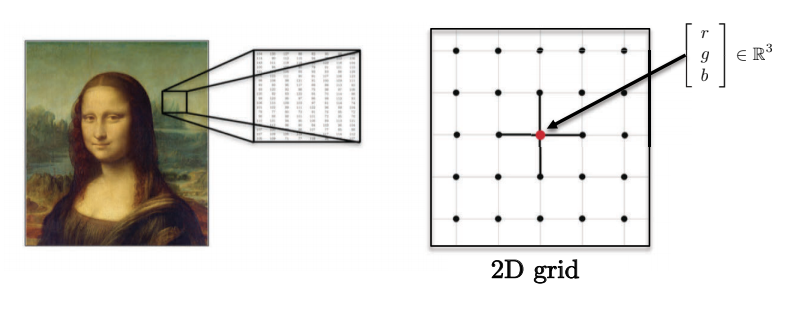
Fig. 4: 이미지는 복수의 차원을 가진다.

• 문장, 단어, 음성은 1D 유클리드 정의역에 놓여있다. 예로, 각 글자는 하나의 정수로 표현되어진다.

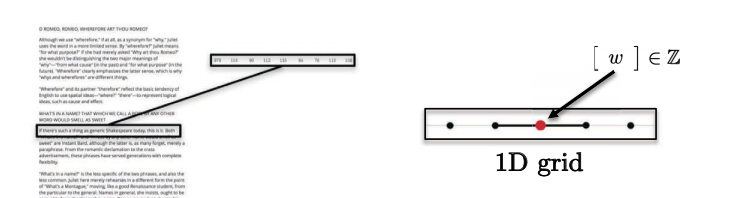
Fig. 5: 순차^Sequences는 하나의 차원을 가진다.

• 이러한 정의역들은 강력한 정칙 공간적 구조^{strong regular spatial structures}들을 가짐으로 합성곱 연산작업을 빠르고 수학적으로 잘 정의되게 한다.

  
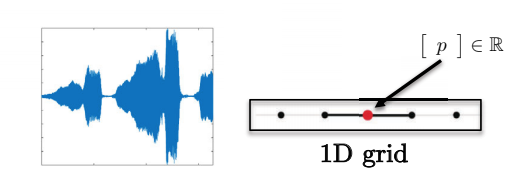
  Fig. 6: 음성 데이터는 1차원의 그리드를 갖는다. </center>

그래프 정의역

그래프 정의역의 예제

소셜 네트워크로 예를 들어보자. 소셜 네트워크는 두 유저 상호 간의 연결이 그리드를 형성하지 않기에 그래프 표현으로는 최적의 대상이다. 그래프의 꼭짓점^Nodes 들은 각 유저를 나타내고, 연결된 간선^edges 들은 유저들 간의 연결을 나타낸다. 각 유저는 메세지, 이미지, 비디오 등을 포함한 3차원 변수 행렬^{feature matrix}을 갖는다.

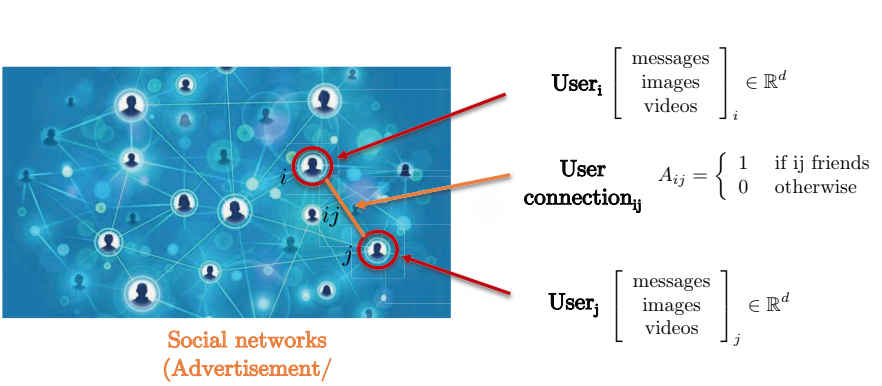
Fig. 7: 그래프로 표현된 소셜 네트워크 .

신경유전병^{neural genetic diseases} 예측하기 위한 뇌의 구조와 역활 연결을 한 예로 들 수 있다. 아래 보기와 같이, 뇌는 여러 개의 관심 영역^{Region of Interest(s) (ROI)}으로 이루어져 있는데, 이러한 관심 영역들은 자신과 인접한 관심 영역들하고만 국부적으로 연결되어있으며, 인집행렬^{Adjacency matrix}은 각기 다른 관심 영역과의 연결 강도^{degree of strength}를 나타낸다.

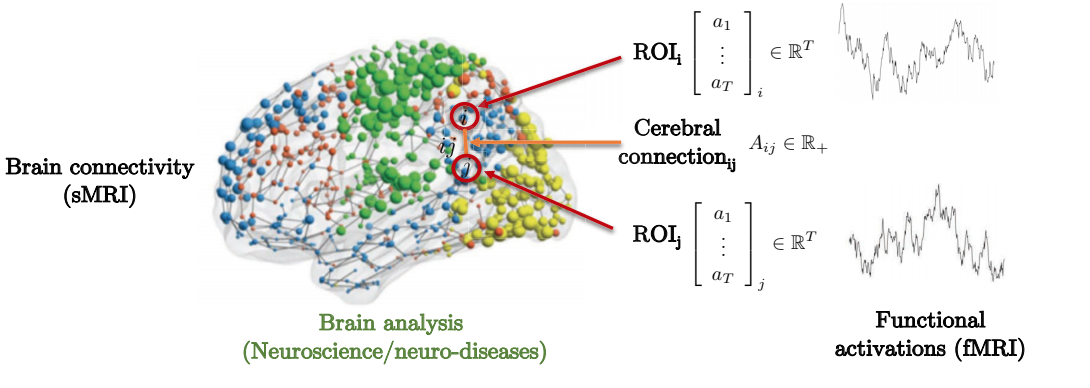
Fig. 8: 두뇌 연결의 그래프적 표현

양자화학 또한 다른 흥미로운 그래프 정의역 표현을 보여준다. 각 원자는 그래프 내에서 꼭짓점으로 표현되며, 다른 원자들과 간선으로 연결된다. 각 분자와 원자들은 전하, 결합의 종류 등 서로 다른 변수들을 갖는다.

그래프 정의와 특징들

• 그래프 G는 다음과 같이 정의된다:
  • 꼭짓점 ^Vertices V
  • 간선^Edges E
  • 인접행렬^{Adjacency matrix} A
• 그래프 변수:
  • 꼭짓점 변수: $h_{i}$, $h_{j}$ (원자 종류)
  • 간선 변수: $e_{ij}$ (결합 종류 bond type)
  • 그래프 변수: g (분자 에너지molecule energy)

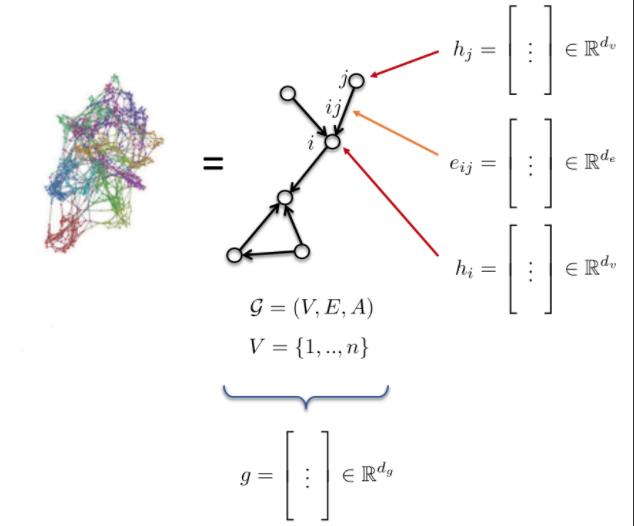
Fig. 10: 그래프

전통적 합성곱 신경망의 합성곱^Convolution

합성곱

합성곱은 다음과 같이 추상적 정의된다:

\(h^{\ell+l} = w^\ell * h^\ell,\) $h^{\ell+1}$는 $n_1\times n_2\times d$-차원을 갖고, $w^\ell$ 는 $3\times 3\times d$-차원을, 그리고 $h^\ell$ 는$n_1\times n_2\times d$-차원을 갖는다.

예를 들어, $n_1$과 $n_2$가 이미지의 $x$와 $y$축 픽셀의 개수고, $d$가 각 픽셀의 차원 수 라고 해보자 (예로 컬러사진은 3의 차원 수를 갖는다).

그렇다면, $h^{\ell+1}$은 $\ell$-번째 은닉망에서의 변수에 합성곱을 적용함으로 얻어진 $(\ell+1)$번째 은닉망의 변수이다.

밑에 이미지를 예로 들어, 커널은 이미지 속에 선들을 인식하는데 사용될 수 있다.

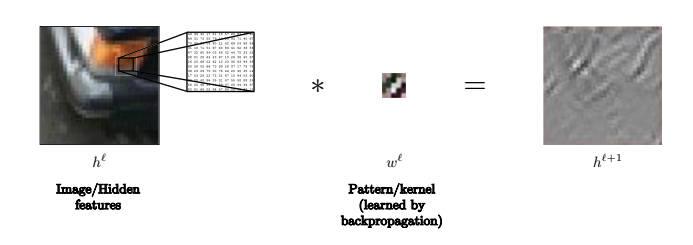
Fig. 11: 커널은 이미지 속에 선들을 인식하는데 사용될 수 있다.

합성곱을 어떻게 정의하나?

좀 더 깊게 설명하자면, 합성곱은 다음과 같이 정의된다:

\[h_i^{\ell_1} = w^\ell * h_i^\ell\] \[= \sum_{j\in\Omega}\langle w_j^\ell, h_{i-j}^\ell\rangle\] \[= \sum_{j\in\mathcal{N}_i} \langle w_j^\ell, h_{ij}^\ell\rangle\] \[=\sum_{j\in\mathcal{N}_i} \langle \Bigg[w_j^\ell\Bigg], \Bigg[h_{ij}\Bigg]\rangle\]

위에서는 합성곱을 템플릿 매칭^{template matching} (형판 대응)이라고 정의하고 있으며, $h_{i-j}$보단 $h_{i+j}$를 사용하는데, 그 이유는 후자가 바로 상관도^correlation이기 때문에 템플릿 매칭에 좀 더 가깝기 때문이다.

세번째 줄에서는 $h_{i+j}^\ell$를 $h_{ij}^\ell$라고 간단히 표기한다.

커널^kernel은 매우 작다. 그래서 두 번째 줄처럼 전체 이미지 $\Omega$에 전부 다 합하는 것보다는 세 번째 줄에 보이는 바와 같이 셀 $i$의 인근 셀들 $\mathcal{N}_i$를 더할 것이다.

위와 같은 작업은 합성곱의 복잡도^complexity 를 $O(n)$로 만드는게 가능하다. ($n$은 입력 이미지 픽셀의 수)

합성곱은 각 $n$개의 픽셀의 $3\times 3$ 그리드에 걸친 $d$차원의 내적 합^{inner products}과 같다.

그래서 복잡도는 $n\cdot 3\cdot 3\cdot d$가 되고 ($O(n)$), GPU를 통해 각 $n$픽셀별로 병렬적^parallel 계산이 가능하다.

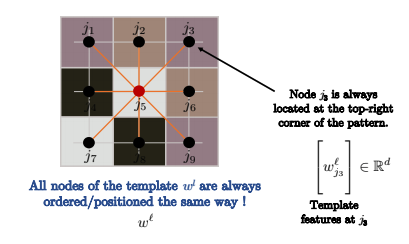
Fig. 12: 점들은 모두 같은 방식으로 정렬된다.

컴퓨터 시각에서의 일반적인 이미지 합성곱처럼, 합성곱되어지는 그래프가 그리드라면, 각 점은 위의 이미지와 같은 방식으로 정렬된다. 그러므로 $j_3$은 항상 패턴의 우측 상단 코너에 위치한다.

그래서 아래 이미지에서의 모든 점 $i$에 대해, 커널의 점 배치순서는 항상 같다. 예를 들어, 아래와 같이 항상 패턴의 우측 상단 코너 $j_3$ 는 (픽셀 $i$에 합성곱이 적용되는) 이미지 패치의 우측 상단 코너와 비교해야 한다.

수학적으로 표현하자면 다음과 같다: \(\langle\Bigg[w_{j_3}^\ell\Bigg], \Bigg[h_{ij_3}^\ell \Bigg]\rangle\)

와

\[\langle\Bigg[w_{j_3}^\ell\Bigg], \Bigg[h_{i'j_3}^\ell \Bigg]\rangle\]

는 항상 템플릿과 이미지 패치의 우측 상단 코너에 대한 것이다.

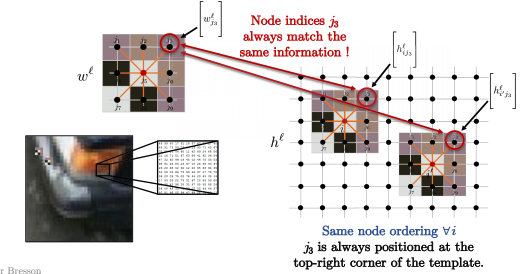
Fig. 13: 템플릿에 맞춰지는 이미지 패치.

템플릿 매치를 그래프에도 적용할 수 있을까?

그렇기에는 여러 가지 문제점이 존재한다:

1. 첫째로, 그래프에는 점들의 순서라는 게 존재하지 않는다.

아래 이미지에서 보이는 것과 같이, 점 $j_3$는 (임의적인) 색인^index만 존재할 뿐, 특정된 장소에 위치하지 않는다. 그래서 점 $i$와 점 $i’$를 아래 그래프와 같이 매치하려 하여도 $j_3$가 두 합성곱에 같은 점과 비교하는지 확인 할 수 없는데, 이는 그래프에 우측 상단 코너 라는 개념이 존재하지 않기 때문이다.

상하좌우 방향의 개념이 존재하지 않기에 템플릿 매칭은 더는 의미가 없게 되고, 위 템플릿 매칭의 정의를 그대로 사용할 수 없다.

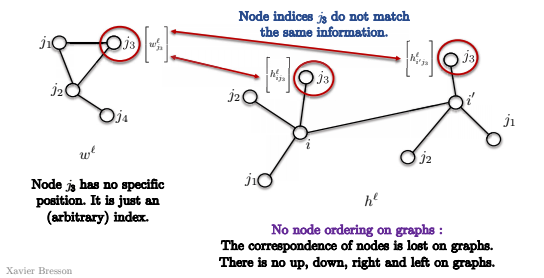
Fig. 14: 그래프에서는 점들의 순서가 없다.

1. 두 번째 문제점은 인접 크기^{neighborhood sizes}가 다를 수 있다는 것이다.

그래서 아래에 보이는 템플릿 $w^\ell$는 인접한 4개의 꼭짓점을 갖는데 점 $i$는 인근에 7개의 점을 가진다. 이 둘을 어떻게 비교할 수 있을까?

그래프 합성곱

이제 그래프의 합성곱 정의를 위해 합성곱 이론^{Convolution Theorem}을 사용해보자.

\[\mathcal{F}(w*h) = \mathcal{F}(w) \odot \mathcal{F}(h) \implies w * h = \mathcal{F}^{-1}(\mathcal{F}(w)\odot\mathcal{F}(h))\]

일반적으로 푸리에 변환^{Fourier transform}은 $O(n^2)$의 복잡도를 갖지만, 정의역이 그리드라면, 복잡도는 고속 푸리에 변환^FFT을 이용해 $O(n\log n)$로 줄일 수 있다.

합성곱 이론을 그래프에도 적용이 가능할까?

이 방식은 두 가지의 의문점을 제기한다:

1. 푸리에 변환을 그래프에 적용하기 위해 어떻게 정의할 것인가?
2. 콤팩트^compact한 커널들을 위해 고속 스펙트럼 합성곱^{fast spectral convolutions}을 어떻게 $O(n)$시간으로 계산할 수 있는가 (템플릿 매칭처럼)?

\[w *_{\mathcal{G}} h \stackrel{?}{=} \mathcal{F}^{-1}_{\mathcal{G}}(\mathcal{F}_{\mathcal{G}}(w)\odot\mathcal{F}_{\mathcal{G}}(h))\]

그래프 신경망을 위해 다음 두 가지의 방법이 사용한다: 템플릿 매칭은 공간적 그래프 합성곱 신경망에, 그리고 합성곱 이론은 스펙트럼 합성곱 신경망에 사용될 것이다.

스펙트럼 그래프 합성곱 신경망

스펙트럼 합성곱은 어떻게 사용되어지나?

1단계: 그래프 라플라시안^Laplacian

그래프 라플라시안은 스펙트럼 그래프 이론의 핵심 연산자이다.

정의

\[\begin{aligned} \mathcal{G}=(V, E, A) & \rightarrow \underset{n \times n}{\Delta}=\mathrm{I}-D^{-1 / 2} A D^{-1 / 2} \\ & \quad \text { where } \underset{n \times n} D=\operatorname{diag}\left(\sum_{j \neq i} A_{i j}\right) \end{aligned}\]

$A$는 인접행렬이고, $\Delta$는 (단위행렬^{identity matrix}에서 행렬$D$에 의해 정규화ehls^normalized 인접행렬을 뺀 것과 같은) 라플라시안이다. $D$는 대각 행렬이고, 대각에 있는 각 원소는 꼭짓점의 차수^{degree of the node}이며, 이를 정규화된 라플라시안이라고 부른다 (이하 문서에서는 편의상 라플라시안으로 표기).

라플라시안은 그래프의 매끄러움^smoothness의 정도로 해석이 가능하다. 다른 표현으로, 국소값^{local value} $h_i$와 $h_i$’의 인접 평균값의 차이이다. 아래 수식에 $d_i$는 꼭짓점 $i$의 차수이며 $\mathcal{N}_{i}$는 꼭짓점 $i$의 이웃점들이다.

\[(\Delta h)_{i}=h_{i}-\frac{1}{d_{i}} \sum_{j \in \mathcal{N}_{i}} A_{i j} h_{j}\]

위 공식은 꼭짓점 $i$의 함수 $h$에 라플라시안을 적용한 것으로, $h_i$값에서 $h_j$의 인근 꼭짓점들의 평균값을 뺀 것과 같다. 기본적으로, 만약 신호가 매우 매끄럽다면, 라플라시안 값이 작을 것이다. 이는 반대로도 마찬가지다.

2단계: 푸리에 함수

다음은 그래프 라플라시안의 고유값 분해^{eigen-decomposition}이다,

\[\underset{n \times n}{\Delta}=\Phi^{T} \Lambda \Phi\]

위 라플라시안은 3가지 행렬 $\Phi ^ T$, $\Lambda$, $\Phi$을 갖는다,

$\Phi$는 아래와 같이 정의되며, 각 $n \times 1$ 크기를 가진 $\phi_1$부터 $\phi_n$까지의 라플라시안 고유 벡터인 열벡터^{column vector}를 갖는다. 각 원소들은 푸리에 함수^{Fourier functions}라고 하며, 푸리에 함수는 정규 직교 기저^{orthonormal basis}를 형성한다.

\[\begin{array}{l}\text { where } \underset{n \times n}{\Delta}\Phi=\left[\phi_{1}, \ldots, \phi_{n}\right]=\text { and } \Phi^{T} \Phi=\mathrm{I},\left\langle\phi_{k}, \phi_{k^{\prime}}\right\rangle=\delta_{k k^{\prime}} \\\end{array}\]

$\Lambda$는 $\lambda_1$부터 $\lambda_n$까지의 라플라시안 고윳값들을 가진 대각행렬이다. 정규화가 적용되었기에 고윳값들은 일반적으로 $0$ 부터 $2$ 사이며, 이는 그래프의 스펙트럼으로도 알려져있다. 아래 함수를 참조.

\[\begin{array}{c}\text { where } \underset{n \times n}\Lambda=\operatorname{diag}\left(\lambda_{1}, \ldots, \lambda_{n}\right) \text { and } 0 \leq \lambda_{1} \leq \ldots \leq \lambda_{n}=\lambda_{\max } \leq 2\end{array}\]

아래는 고유값 분해 확인의 예이다. 라플라시안 행렬 $\Lambda$는 고유 벡터 $\phi_k$와 곱해지며, $n \times 1$의 크기를 가진 결과 $\lambda_k \phi_k$를 갖는다.

\[\begin{array}{ll}\text { and } \underset{n \times 1}{\Delta \phi_{k}}=\lambda_{k} \phi_{k}, & k=1, \ldots, n \\ & \end{array}\]

아래 그림은 1차원 유클리드 라플라시안을 시각화하여 보여준다.

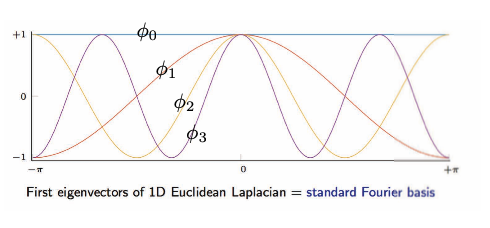
Fig. 16: 그리드/유클리드 정의역: 1차원 유클리드 라플라시안의 고유벡터

그래프 정의역으로는 왼쪽에서 오른쪽 순으로, 첫 번째, 두 번째, 세 번째, .. 그래프의 푸리에 함수들이다. 예를 들어 $\phi_1$은 $\phi_2$, $\phi_3$와 마찬가지로 양수(빨강)와 음수(파랑) 값의 진동을 갖는다. 이 진동은 그래프의 위상^topology 에 영향을 받으며, 이는 중심부, 군집과 같은 그래프의 기하학적 구조^geometry에 연관되어있다. 이는 그래프 군집화^clustering에 상당한 도움이 된다. 아래 참조.

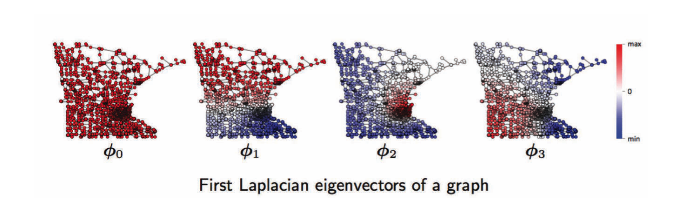
Fig. 17: 그래프 정의역: 그래프의 푸리에 함수.

3단계: 푸리에 변환

\[\begin{aligned} \underset{n \times 1} h &=\sum_{k=1}^{n} \underbrace{\left\langle\phi_{k}, h\right\rangle}_{\mathcal{F}(h)_{k}=\hat{h}_{k}=\phi_{k}^{T} h}\underset{n \times 1}{\phi_{k}} \\ &=\sum_{k=1}^{n} \hat{h}_{k} \phi_{k} \\ &=\underbrace{\Phi \hat{h}}_{ \mathcal{F}^{-1}(\hat{h}) } \end{aligned}\]

푸리에 급수: 함수 $h$를 푸리에 함수로 분해하라.

함수 $h$에 각 푸리에 함수 $\phi_k$에 적용을 시키면, 스칼라인 $k$의 푸리에 급수의 계수^{coefficient of Fourier series}를 갖고, 함수 $\phi_k$에 곱해진다.

푸리에 변환은 단순히 함수 $h$를 푸리에 함수에 적용시킴으로 푸리에 급수의 계수를 찾는 것을 말한다.

푸리에 변환/ 푸리에 급수의 계수

\[\begin{aligned} \underset{n \times 1}{\mathcal{F}(h)} &=\Phi^{T} h \\ &=\hat{h} \end{aligned}\]

역푸리에^{Inverse Fourier Transform} 변환

\[\begin{aligned} \underset{n \times 1}{\mathcal{F}^{-1}(\hat{h})} &=\Phi \hat{h} \\ &=\Phi \Phi^{T} h=h \quad \text { as } \mathcal{F}^{-1} \circ \mathcal{F}=\Phi \Phi^{T}=\mathrm{I} \end{aligned}\]

푸리에 변환은 행렬 $\Phi^{T}$와 벡터 $h$를 곱하는 선형 연산이다.

4단계: 합성곱 이론

두 함수 합성곱의 푸리에 변환은 두 함수 각각의 푸리에 변환끼리의 단순곱^{pointwise product}이다.

\[\begin{aligned} \underset{n \times 1} {w * h} &=\underbrace{\mathcal{F}^{-1}}_{\Phi}(\underbrace{\mathcal{F}(w)}_{\Phi^{T} w=\hat{w}} \odot \underbrace{\mathcal{F}(h)}_{\Phi^{T} h}) \\ &=\underset{n \times n}{\Phi}\left( \underset{n \times 1}{\hat{w}}\odot \underset{n \times 1}{\Phi^{T} h}\right) \\ &=\Phi\left(\underset{n \times n}{\hat{w}(\Lambda)} \underset{n \times 1}{\Phi^{T} h}\right) \\ &=\Phi \hat{w}(\Lambda) \Phi^{T} h \\ &=\hat{w}(\underbrace{\Phi \Lambda \Phi^{T}}_{\Delta}) h \\ &=\underset{n \times n}{\hat{w}(\Delta)} \underset{n \times1}h \\ & \end{aligned}\]

위의 예제는 $w$와 $h$의 합성곱이며, 둘 다 $n \times 1$의 크기를 갖고, $w$와 $h$의 푸리에 변환끼리의 단순곱의 역푸리에 변환과 같다. 위 수식은 $\hat{w}(\Delta)$ 와$h$의 행렬곱과 같다는 걸 보여준다.

그래프 $h$와 $w$의 두 함수 합성곱은 스펙트럼 함수 $w$를 가져다 라플라시안에 적용시켜 $h$와 곱해지며, 이는 스펙트럼 합성곱의 정의이다. 문제는 연산 복잡도가 그래프 $n$ 꼭짓점에 비래하는 $\mathrm{O}\left(n^{2}\right)$이라는 것이다.

한계점

그래프 정의역에서의 스펙트럼 합성곱은 전이 불변^invariance하지 않는다, 다시 말해 위치가 바뀌게 된다면, 그리드/유클리드 정의역이 바뀌지 않음에도 함수의 구조가 변하게 될 수도 있다는 것이다.

권장 도서

Spectral graph theory, Fan Chung, (harmonic analysis, graph theory, combinatorial problems, optimization)

---

📝 Bilal Munawar, Alexander Bienstock, Can Cui, Shaoling Chen
Seok Hoan (Kevin) Choi
27 Apr 2020