어텐션과 트랜스포머

어텐션

트랜스포머 아키텍쳐에 대해 이야기하기에 앞서, 어텐션의 개념에 대해서 소개하겠다. 어텐션은 두 가지 메인 타입이 있다: 셀프 어텐션 vs. 크로스 어텐션, 그 범주안에는 하드 vs. 소프트 어텐션이 있다

나중에 보게되겠지만 시퀀스들이 아니라, 세트들 사이의 매핑^mapping을 하는 어텐션 모듈들로 트랜스포머는 이루어져있다. 이는 입력값/출력값들에 순서를 적용하지 않는다는 뜻이다.

셀프 어텐션 (I)

입력값 $\boldsymbol{x}$의 $t$ 세트를 생각해보자:

각 $\boldsymbol{x}_i$는 $n$-차원의 벡터이다. set이 $t$ 원소들을 갖고 있기에, 각각은 $\mathbb{R}^n$에 속하고, set은 행렬 $\boldsymbol{X}\in\mathbb{R}^{n \times t}$로 표현할 수 있다.

셀프 어텐션에서 은닉 표현^{hidden representation}인 $h$는 입력값들의 선형 조합^{linear combination}이다.

위에 서술한 행렬 표현^{matrix representation}을 써서, 은닉층을 행렬곱으로 써볼 수 있다:

$\boldsymbol{a} \in \mathbb{R}^t$는 요소 $\alpha_i$를 갖고있는 열 벡터이다.

이는 우리가 지금까지 보아온 은닉 표현, 입력값이 가중치 행렬로 곱해지는 것과는 다르다.

벡터 $\vect{a}$에 부여한 제약조건에 따라, 우리는 하드 또는 소프트 어텐션을 해낼 수 있다.

하드 어텐션

하드 어텐션에서, 알파값들에 이와 같은 제약조건들을 건다: $\Vert\vect{a}\Vert_0 = 1$. 이 말은 $\vect{a}$이 원핫 벡터라는 것이다. 그러므로, 입력값들의 선형 조합에서 하나를 제외한 모든 계수는 0과 같으며, 은닉 표현은 요소 $\alpha_i=1$에 해당하는 입력값 $\boldsymbol{x}_i$를 줄인다.

소프트 어텐션

소프트 어텐션에서는, $\Vert\vect{a}\Vert_1 = 1$를 적용한다. 은닉 표현은 계수들의 총합이 1이 되는, 입력값들의 선형 조합이다.

셀프 어텐션 (II)

$\alpha_i$는 어디에서 오는 것일까?

우리는 $\vect{a} \in \mathbb{R}^t$ 벡터를 아래와 같은 방법으로 얻는다:

$\beta$는 $\text{soft(arg)max}(\cdot)$의 반전 온도 파라미터^{inverse temperature parameter}를 대표한다. $\boldsymbol{X}^{\top}\in\mathbb{R}^{t \times n}$는 set $\lbrace\boldsymbol{x}_i \rbrace_{i=1}^t$의 전치 행렬 표현이며, $\boldsymbol{x}$는 set의 일반적인 $\boldsymbol{x}_i$를 대표한다. $X^{\top}$의 $j$-번째 행 요소는 $\boldsymbol{x}_j\in\mathbb{R}^n$에 상응한다는 걸 알아두는 편이 좋다, 따라서 $\boldsymbol{X}^{\top}\boldsymbol{x}$의 $j$-번째 행은, $\lbrace \boldsymbol{x}_i \rbrace_{i=1}^t$에 있는 각 $\boldsymbol{x}_i$과 $\boldsymbol{x}_j$의 스칼라곱이다.

$\vect{a}$ 벡터의 요소들은 “스코어”라고 부른다, 왜냐하면 두 벡터간의 스칼라곱은 두 벡터가 얼마나 비슷한지 얼마만큼 맞춰져있는지 알려주기 때문이다. 따라서, $\vect{a}$의 요소들은 특정한 $\boldsymbol{x}_i$을 위한, 전반적인 세트의 유사도에 대한 정보를 공급한다.

사각 괄호들은 선택사항인 인수^argument를 나타낸다. 만약 $\arg\max(\cdot)$이 사용되면, 우리는 알파들의 원핫 벡터를 얻는다, 하드 어텐션이 되는 것이다. 반면에, $\text{soft(arg)max}(\cdot)$는 소프트 어텐션이 된다. 케이스별로, 결과 벡터 $\vect{a}$의 요소들을 모두 합치면 1이 된다.

이런 방식으로 $\vect{a}$를 생성하는 것은, 각 $\boldsymbol{x}_i$ 당 하나씩 세트를 준다. 더군다나, $\vect{a}_i \in \mathbb{R}^t$별로 우리는 행렬 $\boldsymbol{A}\in \mathbb{R}^{t \times t}$안에 알파들을 쌓을 수 있다.

각 은닉 스테이트가 입력값 $\boldsymbol{X}$와 벡터 $\vect{a}$의 선형 조합이기에, 우리는 $t$개의 은닉 스테이트의 세트를 얻어서, 행렬 $\boldsymbol{H}\in \mathbb{R}^{n \times t}$에 쌓을 수 있다.

키-밸류 저장

키-밸류 저장^{key-value store} 방식은 저장(저장), 받아오기(질의하기) 그리고 관련있는 어레이^arrays를 관리(딕셔너리/해쉬 테이블들)하기 위해 디자인된 패러다임이다.

한 예로, 우리가 라자냐를 만들기 위한 레시피를 찾는다고 해보자. 레시피 책에서 “라자냐”를 검색한다 - 이것이 질의^query이다. 이 질의는 데이터셋에서 모든 가능성있는 키들에 대해서 체크한다 - 이 경우, (키는) 책의 모든 레시피들의 타이틀일 수 있다. 우리가 어떻게 질의를 적용하는지를 체크한다는 건, 질의와 모든 각 키들 사이의 최대가 되는 매칭 스코어를 찾는다는 것이다. 만약 결과값이 최대 인수를 반환하는 함수^{argmax function}면 - 우리는 가장 최고의 스코어를 갖는 하나의 레시피를 받는다.

다른 방법으로는 소프트하게 최대 인수를 반환하는 함수^{soft argmax function}를 쓴다면, 확률 분포를 얻을 수 있고, 질의와 매칭되는 관련성이 덜한 레시피들에, 가장 비슷한 콘텐츠로부터 덜한 콘텐츠도 순서대로 받을 수 있다.

기본적으로 질의는 질문이다. 하나의 질의가 주어지면, 우리는 모든 키에 대하여 이 질의를 체크하고 일치하는 모든 컨텐츠를 검색한다.

질의들, 키와 밸류들

각 벡터들 $\vect{q}, \vect{k}, \vect{v}$은 간단하게 특정 입력값 $\vect{x}$의 회전이라고 볼 수 있다. $\vect{q}$는 $\vect{W_q}$로 회전시킨 $\vect{x}$이고, $\vect{k}$는 $\vect{W_k}$로 회전시킨 $\vect{x}$이며, $\vect{v}$에 대해서도 비슷하다. 우리가 처음으로 “학습가능한” 파라미터들을 소개하고 있음을 기억해둘 필요가 있다. 또한 어텐션이 그 근원에 철저하게 기반하고 있기에 어떤 비선형 (함수들)도 포함하지 않았다.

모든 가능한 키들에 대한 질의를 비교하기 위해, $\vect{q}$과 $\vect{k}$는 반드시 같은 차원수를 가져야 한다. 다른말로 $\vect{q}, \vect{k} \in \mathbb{R}^{d’}$.

그러나, $\vect{v}$는 어떤 차원도 될 수 있다. (위의) 라자냐 레시피 예제를 계속 해보자면 - 키와 같은 차원수를 갖기 위해 질의 해야한다. 우리가 검색하며 지나쳐야하는 다른 레시피들의 타이틀들 말이다.

상응하는 레시피의 차원수를 받으면, $\vect{v}$, 임의로 길 수도 있다. 때문에 우리는 $\vect{v} \in \mathbb{R}^{d’’}$를 갖고 있다.

간단하게 하기 위해, 여기에 모든 것은 차원 $d$를 갖고 있다는 가정을 만들 것이다. 다른말로는

이제 우리는 $\vect{x}$의 세트, 질의 세트, 키 세트, 그리고 밸류 세트들을 갖고 있다. $t$개의 벡터를 쌓은 바 있으므로, 이 세트들을 각각 $t$개의 열을 가진 행렬에 쌓을 수 있다; 각 벡터의 높이는 $d$이다.

하나의 질의 $\vect{q}$를 모든 키 $\vect{K}$ 행렬과 비교해보자:

그럼 은닉층은 $\vect{a}$안에 있는 계수들로 가중치가 책정된, $\vect{V}$ 열들의 선형 조합일 것이다:

$t$개의 질의를 했으므로, $\vect{a}$ 가중치에 상응하는 $t$를 얻을 수 있을 것이다. 따라서 차원수 $t \times t$의 $\vect{A}$ 행렬이 된다:

행렬 표기법으로 보면:

이외에도, 우리는 일반적으로 $\beta$ 세트를:

차원 $d$가 다르게 선택되었다 하더라도 이들을 교차하면서도, 온도 상수^{temperature constant}를 지키기 위해 이렇게 한 것이며, 그래서 $d$ 차원 숫자들의 제곱근으로 나누는 것이다. (벡터 $\vect{1} \in \R^d$의 길이가 무엇일지 생각해보자)

실 적용에서는, 모든 $\vect{W}$를 하나의 긴 $\vect{W}$로 쌓아 연산속도를 높일 수 있으며, 한 번의 실행으로 $\vect{q}, \vect{k}, \vect{v}$를 계산할 수 있다:

여기에는 “헤드” 개념이 있다. 위에서 우리는 하나의 헤드로 한 예제를 봤는데, 여러개의 헤드를 가질 수도 있다. 한 예로, 우리가 $h$개의 헤드를 갖고 있다 해보자, 그러면 우리는 $h$ $\vect{q}$, $h$ $\vect{k}$ 그리고 $h$ $\vect{v}$, 그리고 $\mathbb{R}^{3hd}$ 안에 있는 벡터로 끝이 난다.

하지만, 우리는 여전히 멀티-헤드 밸류를, $\vect{W_h} \in \mathbb{R}^{d \times hd}$를 사용해 원래의 차원수 $\R^d$로 변형할 수 있다. 이는 단지 키-밸류 저장^{key-value store} 방식을 이행하는 한 가지 가능한 방법일 뿐이다.

트랜스포머

어텐션에 대한 지식을 확장하여, 이제 트랜스포머의 근본적인 빌딩 블록들을 설명한다. 특히, 우리는 정방향 패스로 기본 트랜스포머를 지날 것이고, 표준적인 인코더-디코더 형식에서 어텐션이 어떻게 쓰이는 지를 보고 RNNs의 연속적인 아키텍쳐들과 비교해본다.

인코더-디코더 아키텍쳐

이 용어와 익숙해져야 한다. 오토인코더를 시연하는 동안 가장 눈에 띄게 보였고, 이 부분을 이해하기 위한 사전 조건이기 때문이다. 요약하자면, 입력값은 인코더와 디코더를 통과하는데, 가장 중요한 정보만 지나도록 강제하는, 데이터에 대한 병목지점을 부여하는 것이다. 이 정보는 인코더 블록의 출력값에 저장되고, 상관없는 다양한 과제들에도 쓸 수 있다.

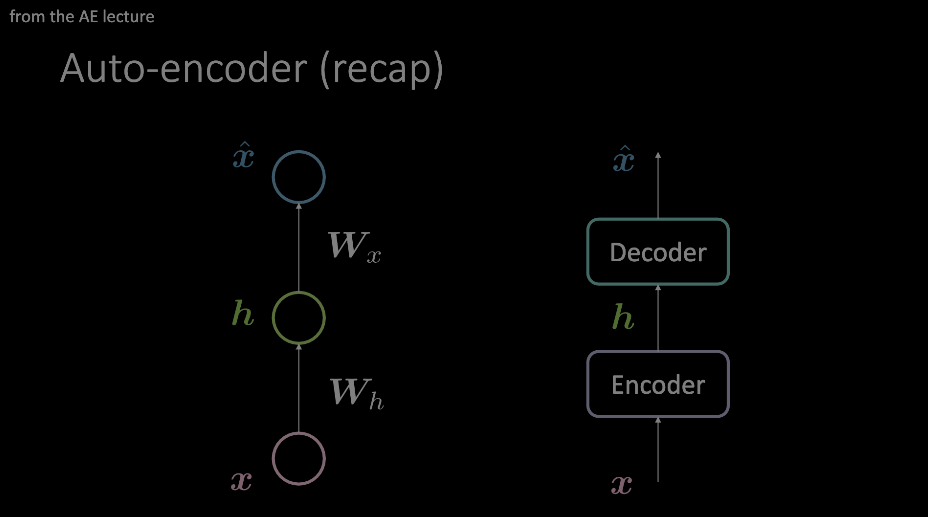
그림 1: 오토 인코더의 두 예제 다이어그램이다. 왼쪽 모델은 오토인코더가 두 개의 어파인 변환 + 활성화 (함수들)을 사용해 어떻게 디자인될 수 있는지를 보여주며, 오른쪽 이미지는 이 단일 "레이어"를 임의의 작업 모듈로 대체했다.

오른쪽 모델에서 보여지듯 “어텐션”은 오코인코더 레이아웃으로 그려졌다. 이제 트랜스포머의 맥락에서, 내부를 들여다보자.

인코더 모듈

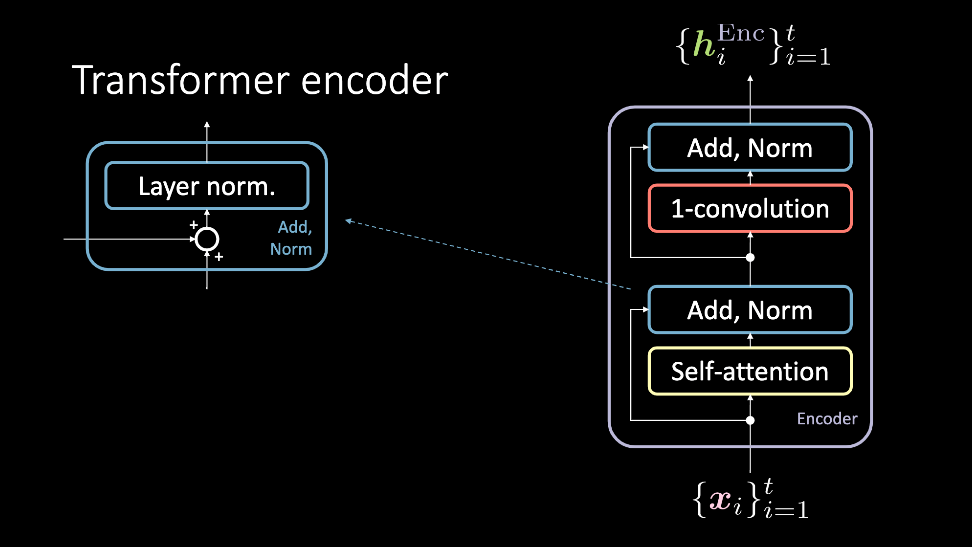
그림 2: 트랜스포머 인코더는, 입력값들의 세트 $\vect{x}$를 받아서 은닉 표현들의 세트인 $\vect{h}^\text{Enc}$를 출력값으로 내놓는다.

인코더 모듈은 입력값들의 세트를 받아, 셀프 어텐션 블록과 이를 우회한 더하기, 정규화 블록에 동시에 먹여서 통과하게끔 한다. 어느 시점에서는, 이들은 다시 1D-합성곱과 또 다른 더하기, 정규화 블록을 동시에 지나가고는, 결과적으로 은닉 표현 세트와 같은 출력물을 낸다. 이 은닉 표현 세트는 이후에 몇몇 인코더 모듈(즉, 더 많은 레이어들)을 통과해서 보내지거나, 디코더로 가거나 한다. 이제 이 블록들을 더 자세히 보자.

셀프 어텐션

셀프-어텐션 모델은 일반적인 어텐션 모델이다. 연속적인 입력값의 같은 아이템으로부터 쿼리, 키, 그리고 밸류가 생성된다. 과제에서 우리는 연속적인 데이터를 모델링하려고 노력하며, 포지셔널 인코딩이 이 입력값에 사전 확률로 추가된다. 이 블록의 출력값은 어텐션-가중치가 부여된 값들이다. 셀프-어텐션 블록은 입력값들의 세트를 $1, \cdots , t$로부터 받고, 출력값으로 $1, \cdots, t$ 어텐션-가중치가 부여된 값들을 내놓는다. 이들은 인코더의 나머지 부분에 넣어져서 지나간다.

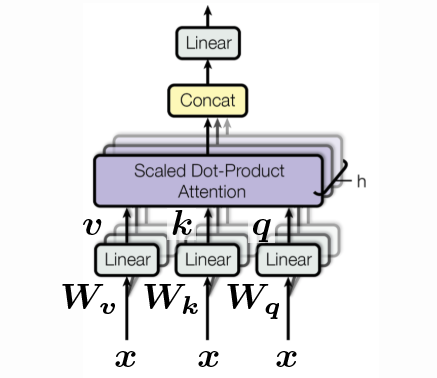
그림 3: 셀프-어텐션 블록. 입력값들의 시퀀스는 3번째 차원을 따라가는 것으로 보여지며, 연결된다.

더하기, 정규화

더하기 정규화 블록은 두 개의 요소를 갖고 있다. 첫번째는 잔차 커넥션인 더하기 블록과 레이어 정규화이다.

1D-합성곱

이 스텝을 따라, 1D-합성곱 (위치 맞춤^{position-wise} 정방향 네트워크라고도 한다)을 적용한다. 이 블록은 두 개의 완전연결 레이어로 구성되어 있다. 어떤 값을 세팅하느냐에 따라, 이 블록은 출력값 $\vect{h}^\text{Enc}$의 차원을 맞추게 해줄 것이다.

디코더 모듈

트랜스포머 디코더는 인코더와 비슷한 과정을 거친다. 하지만, 여기에는 부수적인 하나의 서브블록을 고려해야 한다. 게다가, 이 모듈에 들어가는 입력값들도 다르다.

그림 4: 디코더의 친숙한 설명

크로스 어텐션

크로스 어텐션은 셀프 어텐션 블록에서 쓰였던 쿼리, 키, 그리고 밸류 셋업을 따라간다. 그러나, 입력값들은 약간 더 복잡하다. 디코더에 들어가는 입력값은 셀프 어텐션과 더하기 정규화 블록들을 지나치게 될 $\vect{y}_i$의 데이터 포인트이며, 결국에는 크로스-어텐션 블록에 간다.

이는 크로스 어텐션을 위한 쿼리로 동작한다. 키와 밸류 페어는 $\vect{h}^\text{Enc}$의 출력값이다. 이 출력값은 과거 입력값들인 $\vect{x}_1, \cdots, \vect{x}_{t}$와 함께 계산된다.

요약본

세트 $\vect{x}_1$에서 $\vect{x}_{t}$는 인코더에 들어가서 통과한다. 셀프 어텐션과 몇 개의 블록들을 더 사용하는 것으로, 디코더에 들어갈 출력값의 표현 $\lbrace\vect{h}^\text{Enc}\rbrace_{i=1}^t$을 얻을 수 있다.

셀프 어텐션이 적용된 다음, 크로스 어텐션이 적용된다. 이 블록에서, 쿼리는 목표하는 언어 $\vect{y}_i$ 내부적 심볼 표현에 해당한다. 그리고 키와 밸류는 ($\vect{x}_1$ to $\vect{x}_{t}$)로부터 온다.

직관적으로, 크로스 어텐션은 $\vect{y}_t$를 설계하는데에 가장 관련이 있는, 입력값 시퀀스 안에 있는 밸류를 찾는다. 그래서 최상의 어텐션 계수를 갖는다. 이 크로스 어텐션의 출력물은 또 다른 1D-합성곱 서브 블록을 통과해서 들어가고, 우리는 $\vect{h}^\text{Dec}$를 얻는다. 목표 언어를 말하기 위해, 여기부터 쭈욱 트레이닝이 어떻게 시작하는지, 몇몇 목표 데이터에 $\lbrace\vect{h}^\text{Dec}\rbrace_{i=1}^t$를 비교하는 것으로 보자.

단어 언어 모델

트랜스포머의 가장 중요한 모듈들에 대해 설명 하기 전에, 몇몇 중요한 항목들을 남겨뒀었다. 그러나 이제 트랜스포머가 언어 과제에서 SOTA 결과를 어떻게 달성할 수 있었는지 이해하기위해, 논의를 할 때인 것 같다.

포지셔널 인코딩

어텐션 매커니즘은 모델의 트레이닝 시간을 상당히 가속시켜주는, 동작의 병행 처리를 가능케 하지만, 연속적인 정보를 잃어버린다. 이 맥락^{context을 포지셔널 인코딩은 잡게 해준다.}

의미론적 표현

트랜스포머의 트레이닝 과정 동안, 많은 은닉 표현들이 생성된다. 파이토치의 단어-언어 모델^{word-language model} 예제에서 쓰였던 것과 비슷한 임베딩 공간을 생성하기 위해서, 크로스 어텐션의 출력값은, 단어 $x_i$의 의미론적인 표현을 같은 데이터셋의 차후 실험작업이 이루어지는 포인트에 넣어준다.

코드 요약본

우리는 이제 위에서 논의한 트랜스포머의 블록들을, 더 이해하기 쉬운 포맷으로 볼 것이다. 코드로 말이다!

우리가 볼 첫번째 모듈은 멀티-헤드 어텐션 블록이다. 쿼리, 키, 그리고 밸류들에 의존하여 이 블록으로 들어가고, 이는 셀프 아니면 크로스 어텐션에 사용될 수 있다.

class MultiHeadAttention(nn.Module):
    def __init__(self, d_model, num_heads, p, d_input=None):
        super().__init__()
        self.num_heads = num_heads
        self.d_model = d_model
        if d_input is None:
            d_xq = d_xk = d_xv = d_model
        else:
            d_xq, d_xk, d_xv = d_input
        # 모델의 임베딩 차원은 헤드 숫자의 배수이다.
        assert d_model % self.num_heads == 0
        self.d_k = d_model // self.num_heads
        # 이들은 여전히 d_model의 차원이다. 헤드의 개수대로 나누기 위해서
        self.W_q = nn.Linear(d_xq, d_model, bias=False)
        self.W_k = nn.Linear(d_xk, d_model, bias=False)
        self.W_v = nn.Linear(d_xv, d_model, bias=False)
        # 모든 서브 레이어들의 결과값들은 d_model의 차원이어야 한다
        self.W_h = nn.Linear(d_model, d_model)

멀티-헤드 어텐션 클래스의 초기화. 만약 d_input이 공급되면, 이는 크로스 어텐션이 된다. 아니면, 셀프-어텐션이 된다. 쿼리, 키, 밸류 셋업은 입력값 d_model의 선형 변환으로 만들어진다.

def scaled_dot_product_attention(self, Q, K, V):
    batch_size = Q.size(0)
    k_length = K.size(-2)

    # d_k로 스케일링하는 것은 soft(arg)max가 포화되지 않게 하기 위함이다
    Q = Q / np.sqrt(self.d_k)  # (bs, n_heads, q_length, dim_per_head)
    scores = torch.matmul(Q, K.transpose(2,3))  # (bs, n_heads, q_length, k_length)

    A = nn_Softargmax(dim=-1)(scores)  # (bs, n_heads, q_length, k_length)

    # 밸류들의 가중 평균을 얻는다
    H = torch.matmul(A, V)  # (bs, n_heads, q_length, dim_per_head)

    return H, A

어텐션 벡터로 스케일링을 마치고, 밸류의 인코딩에 상응하는 은닉층을 반환한다. 장부에 기입할 목적으로 (시퀀스의 어떤 밸류들을 어텐션으로 마스킹할것인가?) A 역시도 반환된다.

def split_heads(self, x, batch_size):
    return x.view(batch_size, -1, self.num_heads, self.d_k).transpose(1, 2)

마지막 차원수를 (heads × depth)로 나눈다. 전치한 다음에 반환된 것은 (batch_size × num_heads × seq_length × d_k)의 모양으로 바뀐다.

def group_heads(self, x, batch_size):
    return x.transpose(1, 2).contiguous().
        view(batch_size, -1, self.num_heads * self.d_k)

어텐션 헤드들을 함께 결합시켜서, 배치 사이즈와 시퀀스의 길이로 올바른 형태를 유지한다.

def forward(self, X_q, X_k, X_v):
    batch_size, seq_length, dim = X_q.size()
    # After transforming, split into num_heads
    Q = self.split_heads(self.W_q(X_q), batch_size)
    K = self.split_heads(self.W_k(X_k), batch_size)
    V = self.split_heads(self.W_v(X_v), batch_size)
    # Calculate the attention weights for each of the heads
    H_cat, A = self.scaled_dot_product_attention(Q, K, V)
    # Put all the heads back together by concat
    H_cat = self.group_heads(H_cat, batch_size)  # (bs, q_length, dim)
    # Final linear layer
    H = self.W_h(H_cat)  # (bs, q_length, dim)
    return H, A

이게 멀티 헤드 어텐션의 정방향 패스다.

주어진 입력값은 q, k 그리고 v로 나눠져서 스케일 조정된 내적 어텐션 매커니즘^{scaled dot product attention mechanism}을 통과하고, (요소끼리) 연결한 다음에는 마지막 선형 레이어까지 통과한다. 어텐션 블록의 마지막 결과물은 어텐션이 발견되고, 남은 블록들로 통과하는 은닉 표현이 된다.

트랜스포머/인코더에 보여지는 다음 부분은 더하기, 정규화 블록이지만, 파이토치^PyTorch에 이미 함수가 구현이 되어 있다. 매우 쉽게 적용할 수 있으며, (이 블록만을 위한) 클래스가 필요하지도 않다. 다음은 1D-합성곱 블록이다. 세부적인 것들은 이전 섹션을 참고하기를 바란다.

이제 메인 클래스들을 모두 구축했다, 이제 인코더 모듈로 전환해보자.

class EncoderLayer(nn.Module):
    def __init__(self, d_model, num_heads, conv_hidden_dim, p=0.1):
        self.mha = MultiHeadAttention(d_model, num_heads, p)
        self.layernorm1 = nn.LayerNorm(normalized_shape=d_model, eps=1e-6)
        self.layernorm2 = nn.LayerNorm(normalized_shape=d_model, eps=1e-6)

    def forward(self, x):
        attn_output, _ = self.mha(x, x, x)
        out1 = self.layernorm1(x + attn_output)
        cnn_output = self.cnn(out1)
        out2 = self.layernorm2(out1 + cnn_output)
        return out2

가장 성능이 좋은 트랜스포머들에서, 임의로 많은 수의 인코더가 각자 위에 쌓여있다.

셀프 어텐션 그 스스로는 어떤 순회^recurrence나 합성곱^{convolutions도 갖고 있지 않음을 상기하자, 하지만 그렇기에 빠르게 실행할 수 있기도 하다. 위치에 영향을 받게 하기 위해, 포지셔널 인코딩을 넣자. 이는 아래처럼 계산된다:}

더 세부적인 부분을 할애할 공간이 없어서, 여기에 쓰인 전체 코드를 알려주겠다.

https://github.com/Atcold/pytorch-Deep-Learning/blob/master/15-transformer.ipynb

전체 인코더는 N개의 인코더 레이어가 쌓인 것이고, 포지션 임베딩도 그러하다. 이를 적어보면

class Encoder(nn.Module):
    def __init__(self, num_layers, d_model, num_heads, ff_hidden_dim,
            input_vocab_size, maximum_position_encoding, p=0.1):
        self.embedding = Embeddings(d_model, input_vocab_size,
                                    maximum_position_encoding, p)
        self.enc_layers = nn.ModuleList()
        for _ in range(num_layers):
            self.enc_layers.append(EncoderLayer(d_model, num_heads,
                                                ff_hidden_dim, p))
    def forward(self, x):
        x = self.embedding(x) # Transform to (batch_size, input_seq_length, d_model)
        for i in range(self.num_layers):
            x = self.enc_layers[i](x)
        return x  # (batch_size, input_seq_len, d_model)

예제 사용

인코더만 사용해서 할 수 있는 많은 과제들이 있다. 노트북(코드)과 함께, 인코더를 감성 분석에 어떻게 사용할 수 있는지 보자.

IMDB 리뷰 데이터셋을 사용하여, 인코더로부터 연속된 텍스트의 잠재 표현^{latent representation} 결과물을 얻을 수 있다. 그리고 이 인코딩 프로세스를, 긍정적인지 부정적인 영화 리뷰인지에 상응하는 이진 교차 엔트로피^{binary cross entropy}로 트레이닝한다.

기본적인 것들은 남겨두었으니, 노트북으로 가자. 하지만 여기 트랜스포머에서 쓰이는 가장 중요한 아키텍쳐 요소가 있다.

class TransformerClassifier(nn.Module):
    def forward(self, x):
        x = Encoder()(x)
        x = nn.Linear(d_model, num_answers)(x)
        return torch.max(x, dim=1)

model = TransformerClassifier(num_layers=1, d_model=32, num_heads=2,
                         conv_hidden_dim=128, input_vocab_size=50002, num_answers=2)

이 모델이 보편적인 방식으로 트레이닝 되는 부분이다.