예측과 불확실성에서의 정책 학습

소개 및 문제 설정

우리가 모델 없는 강화학습 방법으로 어떻게 운전하는지 배우고 싶다고 말해보자. 우리는 모델이 실수하고 그 실수에서 배우는 것으로써 강화학습^RL에서 모델들을 학습시킨다. 그렇지만 이것은 학습 요점이 없는 곳에서 실수가 우리를 천국 혹은 지옥으로 데려갈 수 있기 때문에 최선의 방식은 아니다.

그래서, 더 ‘인간’적인 방식으로 운전하는 방법에 대해 이야기해보려 한다. 차선 변경을 예로 들어보자. 차가 시속 100km(약 30m/s)로 움직이고 있다고 가정하고, 30m 앞을 본다면 우리는 약 1초 후의 미래를 내다보고 있는 것이다.

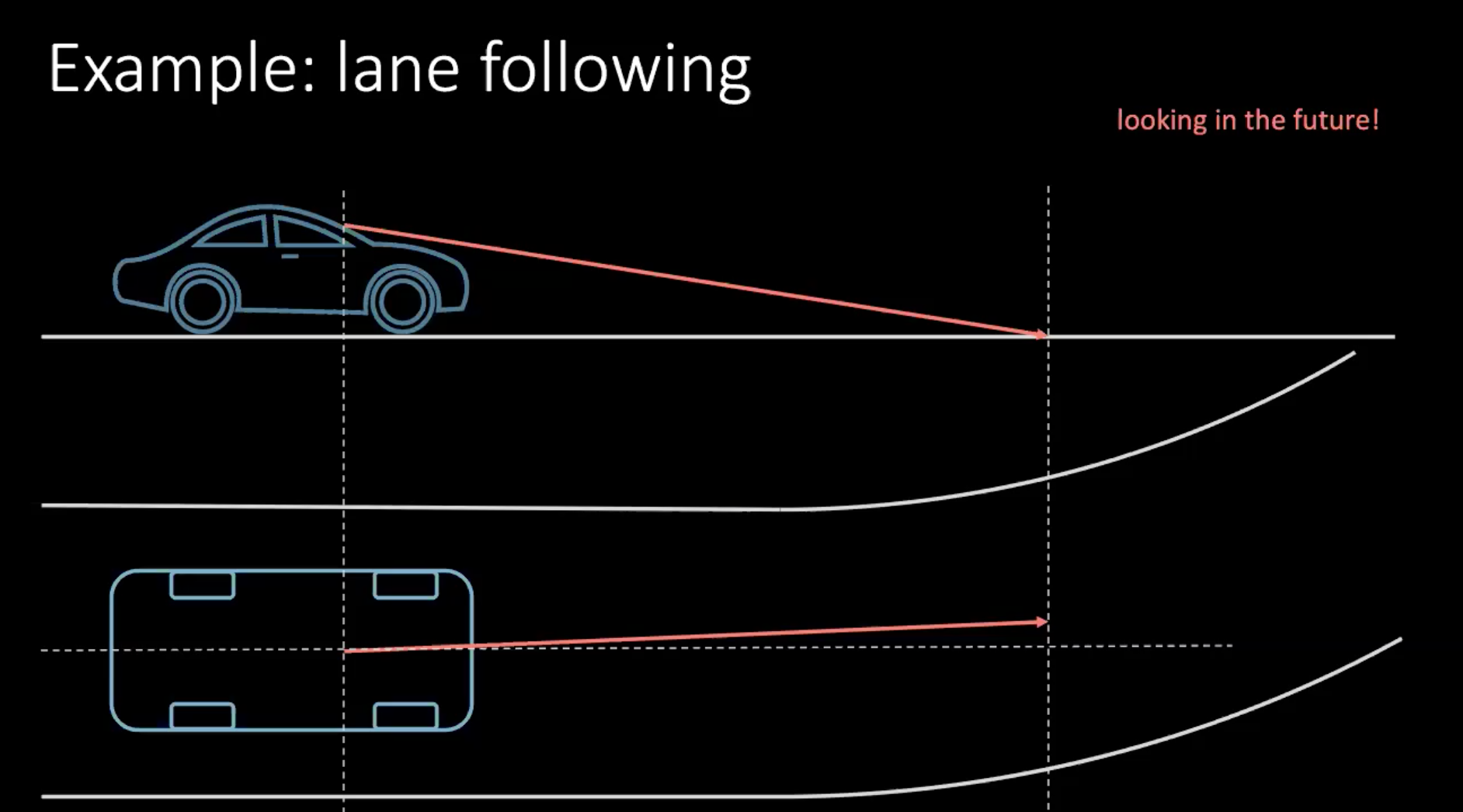
그림 1: 운전 중 미래 예상 하기

만약 방향을 틀고 있었다면, 가까운 미래에 근거하여 결정해야 한다. 불과 몇 미터 안에 회전하려면 핸들을 돌리는 행동을 취해야 한다. 이러한 상황에서 결정하는 것은 주행뿐만 아니라 주변 교통 상황에도 달려있다. 우리 주변의 모든 이가 그렇게 결정을 잘 내리는 편이 아니기 때문에 모든 가능성을 생각한다는 것은 매우 어려운 일이다.

이제 이 시나리오에서 일어나는 일들을 살펴보자. 우리는 (여기서 뇌에 의해 표현된) 입력값 $s_t$(위치, 속도 그리고 문맥 이미지)를 가져오고 행동 $a_t$(핸들 조종, 가속 그리고 정지)를 생성하는 에이전트를 가지고 있다. 환경은 우리를 새로운 상태로 옮기고 비용 $c_t$를 반환한다.

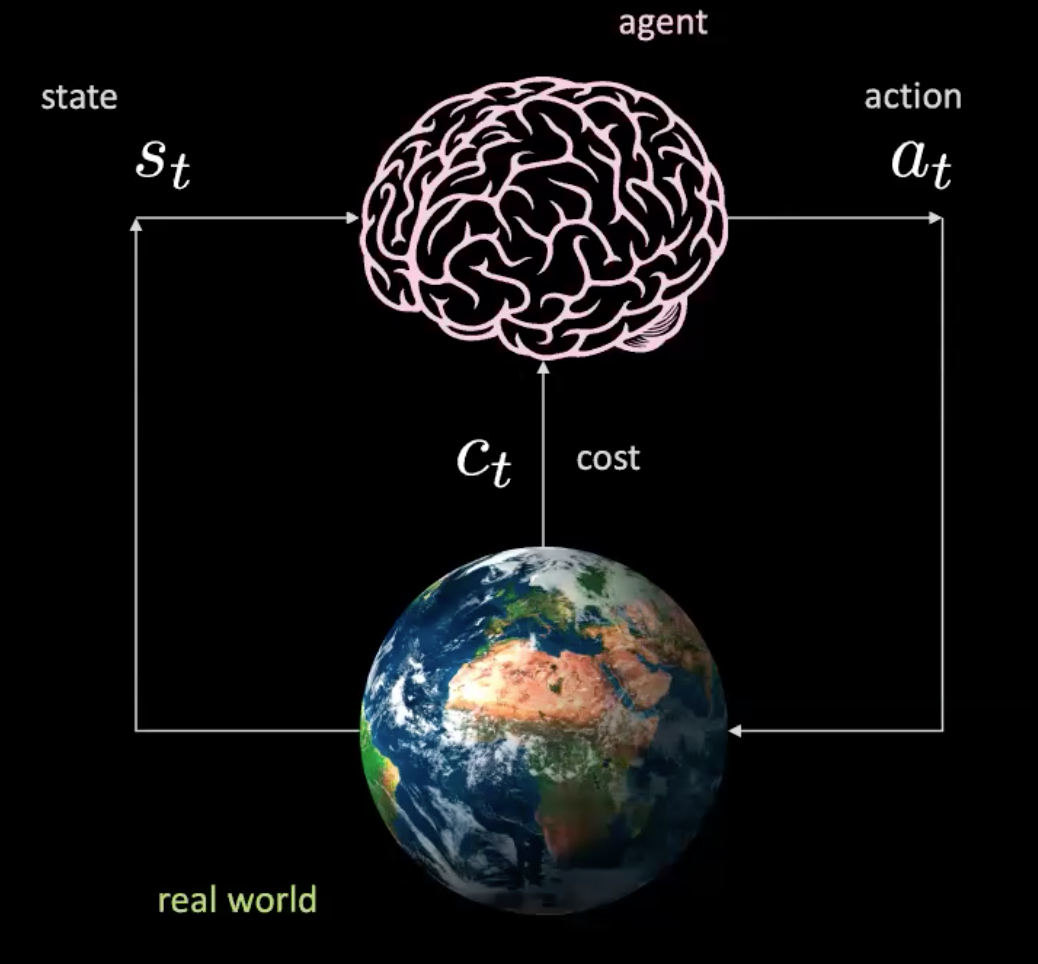
그림 2: 현실 세계의 에이전트 그림

이는 마치 특정 상황에서 행동을 취하고 세계가 새로운 상태와 다음 결과를 주는 곳의 단순 신경망과 같다. 이것은 우리가 현실 세계에서 모든 행동에 대하여 상호작용하고 있기 때문에 모델이 없다. 하지만 실제 현실 세계와의 상호작용이 없는 에이전트를 학습시킬 수 있을까?

그렇다, 할 수 있다! 이제 “학습 세계 모델”에서 알아보자.

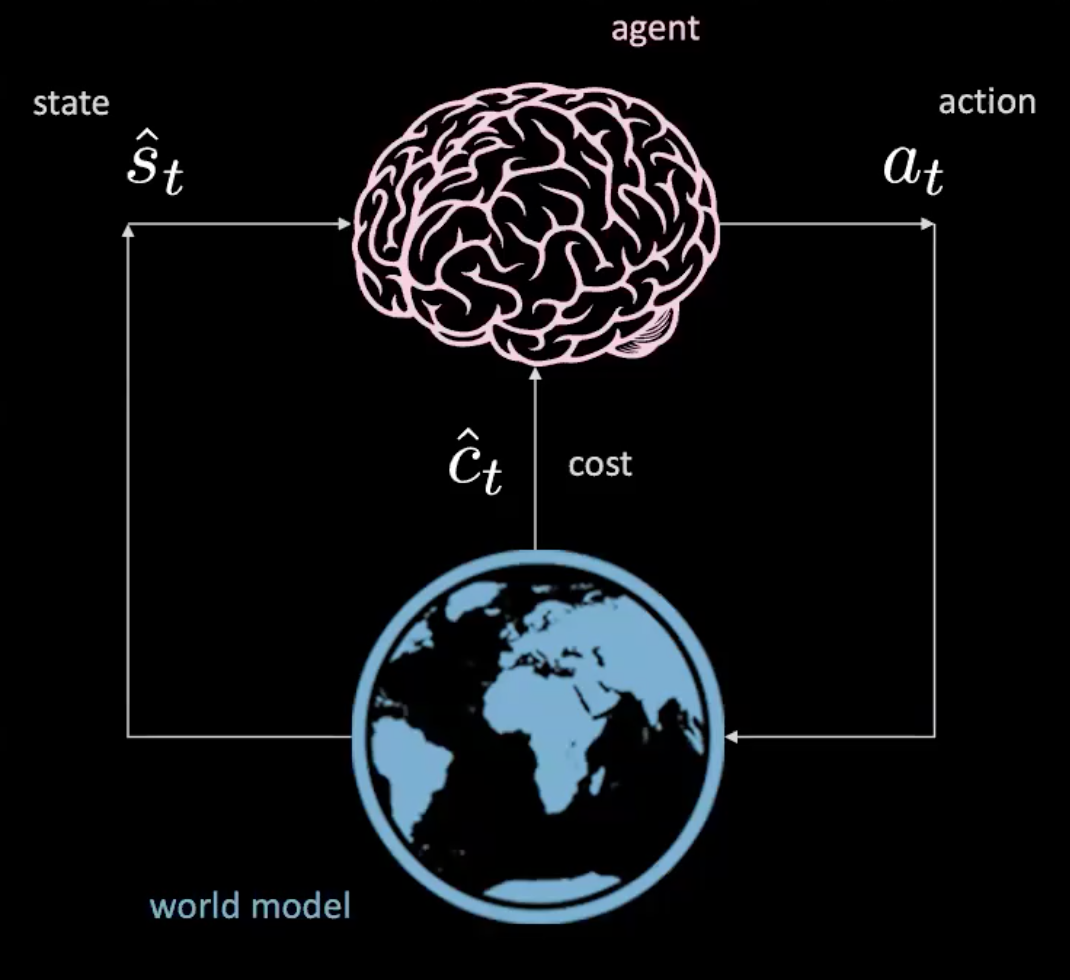
그림 3: 세계 모델의 에이전트 그림

데이터셋

세계 모델 학습 방법을 논하기에 앞서, 우리가 가진 데이터셋을 살펴보자. 우리는 탑-다운 뷰를 얻고 각 차량에 대한 경계 박스를 추출하기 위해 카메라를 조정한다. 시각 $t$일 때, 우리는 위치 $p_t$, 속도 $v_t$ 그리고 차량 주변의 현재 교통 상황을 나타내는 $i_t$를 정할 수 있다.

운전 운동학을 알기 때문에, 운전자 어떤 행동을 하는지 알아내기 위하여 데이터셋을 뒤집을 수 있다. 예를 들어, 만약 차가 등속 직선 운동하고 있다면, 우리는 가속도가 0인 것을 알 수 있다.(행동 없음 의미)

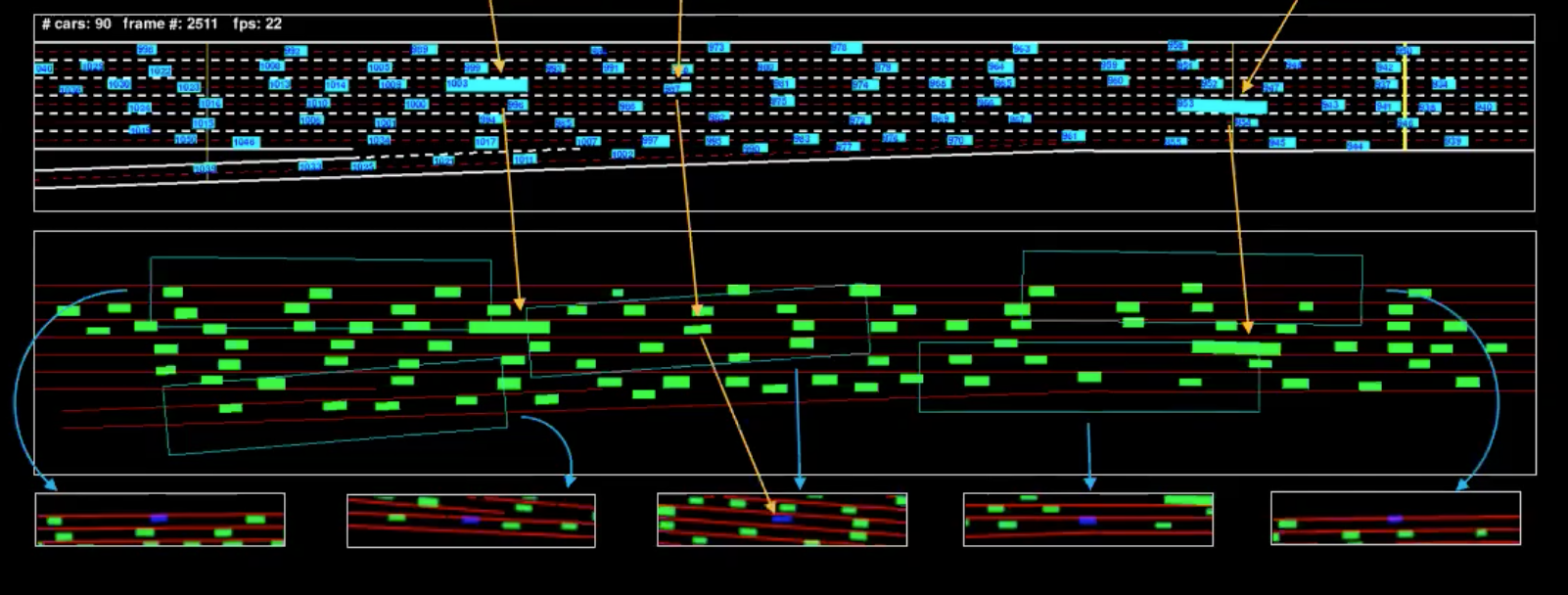
그림 4: 단일 프레임의 기계 표현

파란색 부분은 피드 그리고 초록색 부분은 기계 표현이라고 부를 수 있는 것이다. 원활한 이해를 돕자면 우리는 (그림에 표시된) 자동차 몇 대를 분리했다. 아래 보이는 시점은 이 차량 시야의 경계 상자들이다.

비용

여기 두 가지 유형의 비용이 있다: 차선 비용과 근접 비용이다. 차선 비용은 우리가 차선 유지를 얼마나 잘하고 있는지 알려주고 근접 비용은 다른 차에 얼마나 가까이 붙어있는지 알려준다.

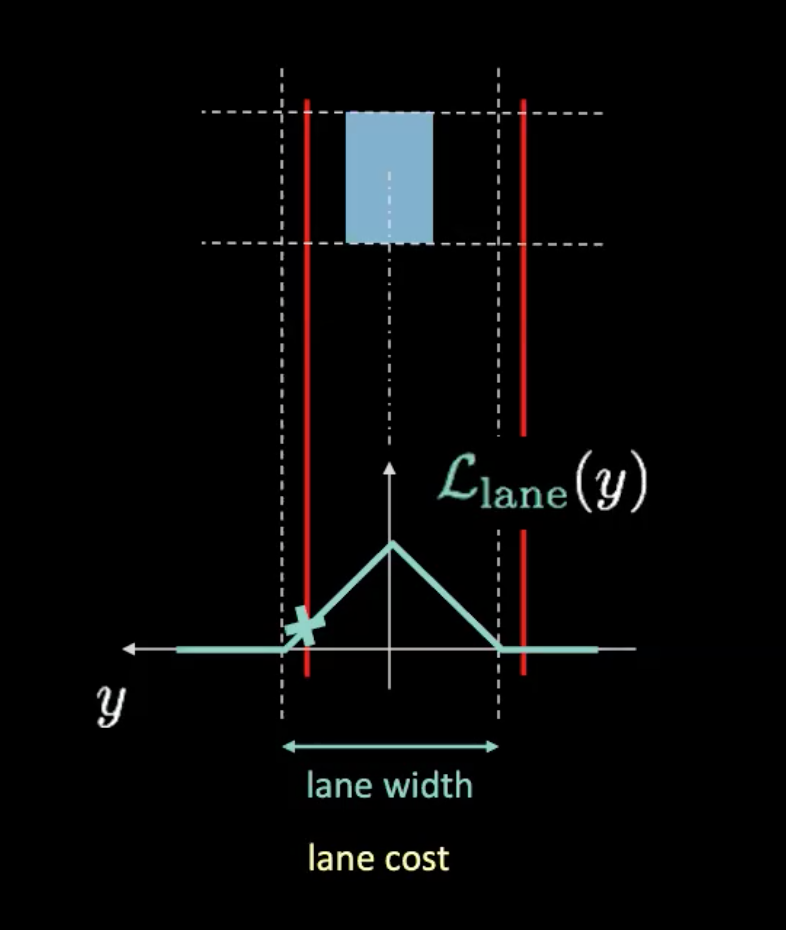
그림 5: 차선 비용

위 그림에서 점선은 실제 차선을 그리고 빨간선은 차량의 현재 위치가 주어진 차선 비용을 알아낼 수 있게 도와준다. 빨간선은 차량의 움직임을 따라간다. 빨간선과 전위 곡선의 교차점 높이(청록색)은 비용을 준다. 만약 차가 중앙선에 있다면, 두 빨간선은 비용이 0인 결과를 만드는 실제 차선과 겹친다. 반면, 차가 중앙에서 멀어짐으로써 빨간선은 또한 비용이 0이 아닌 결과를 만드는 쪽으로 움직인다.

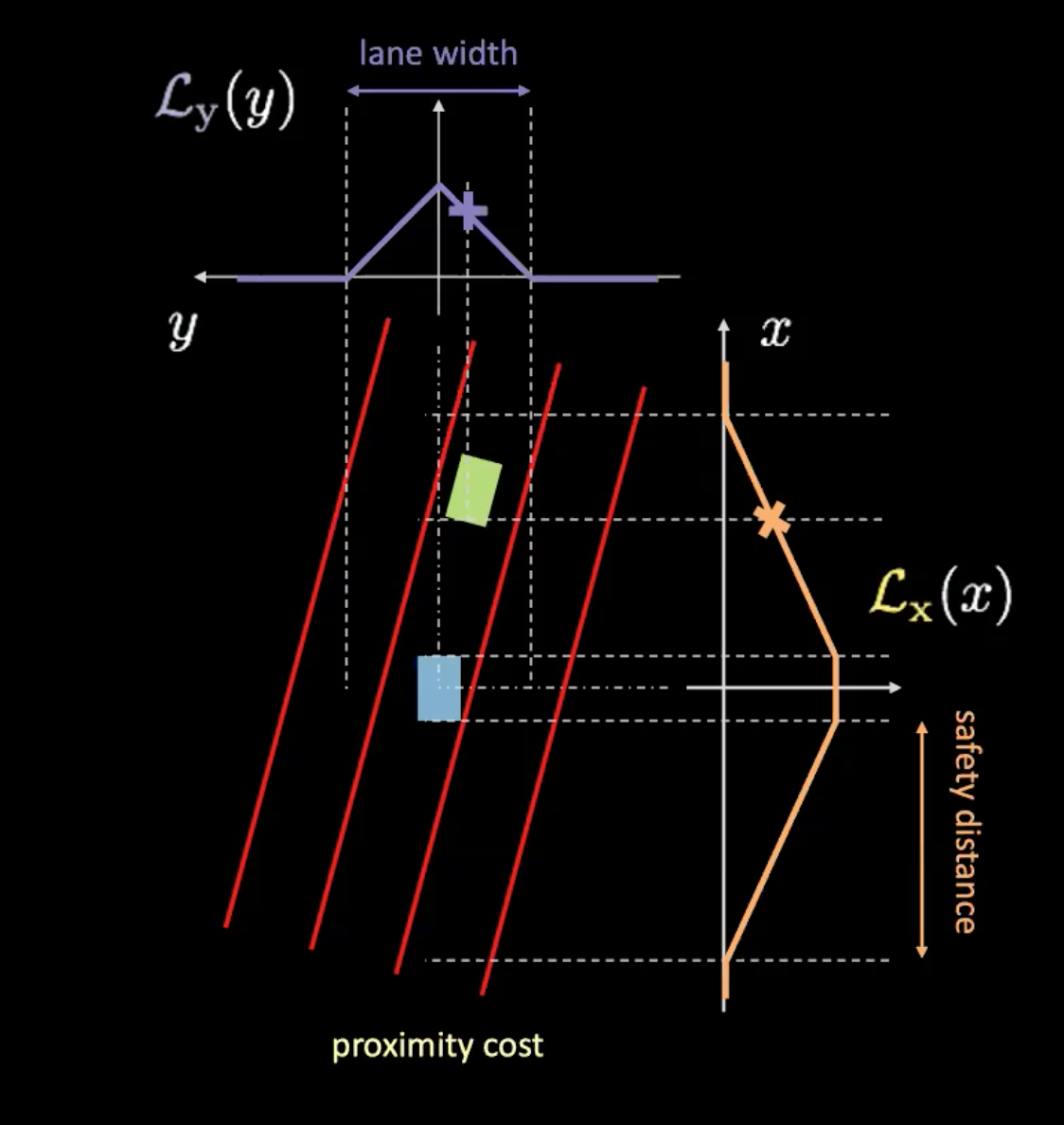
그림 6: 근접 비용

근접 비용은 두 개의 요소($\mathcal{L}_x$ and $\mathcal{L}_y$)를 갖는다. $\mathcal{L}_y$는 차선 비용과 유사하고 $\mathcal{L}_x$는 차량 속도에 따라 달라진다. 그림6의 주황색 곡선은 안전 거리에 대해 알려준다. 차량 속도가 증가함에 따라 주황색 곡선이 커지게 된다. 차가 매우 빠른 속도로 움직이면, 앞뒤로 더 자세히 봐야할 것이다. 차와 주황색 곡선의 교차지점 높이는 $\mathcal{L}_x$를 결정한다.

이 두 요소의 곱은 근접 비용을 준다.

세계 모델 학습하기

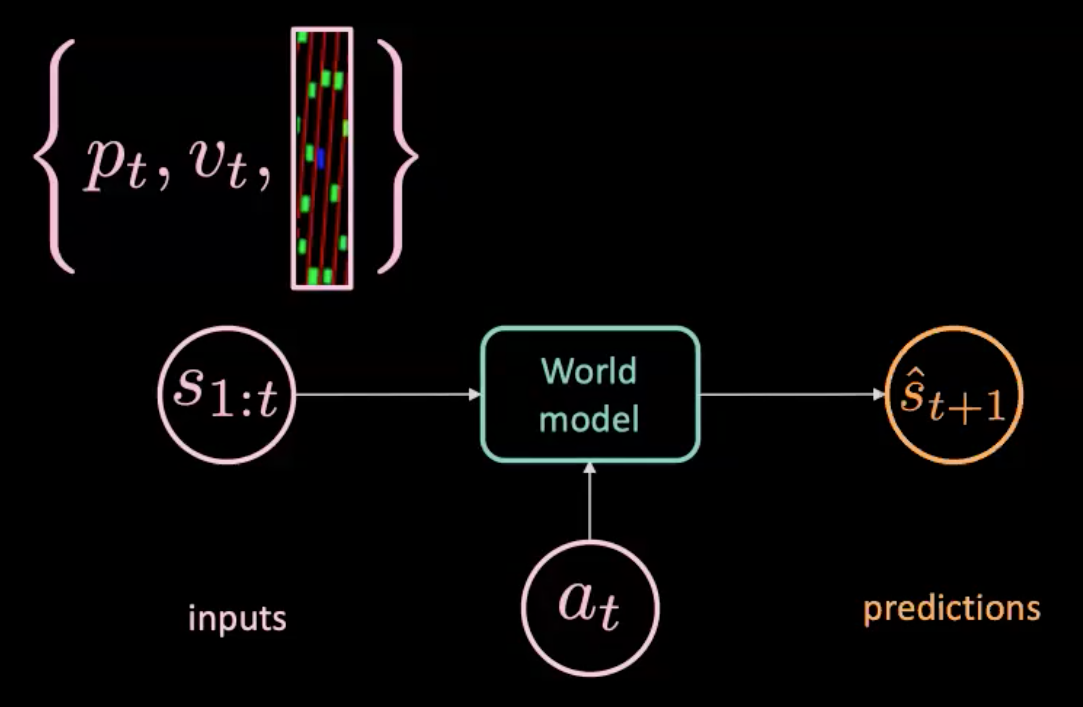
그림 7: 세계 모델 개념도

세계 모델은 행동 $a_t$(스티어링, 브레이크 그리고 가속)와 $s_{1:t}$(시간에 따라 위치, 속도 그리고 전후 이미지가 나타내는 곳에서의 순서)를 공급받고 다음 상태 $\hat s_{t+1}$를 예측한다. 반면, 실제 일어났다는 것($s_{t+1}$)을 알려주는 실제 세계를 가지고 있다. 이에 모델을 학습시키기 위하여 예측값 ($\hat s_{t+1}$)와 목표값 ($s_{t+1}$) 사이의 평균 제곱 오차^MSE를 최적화한다.

결정론적 예측 변수-디코더

모델 학습을 위한 한 가지 방법은 아래에 제시된 예측 변수-디코더 모델을 사용하는 것이다.

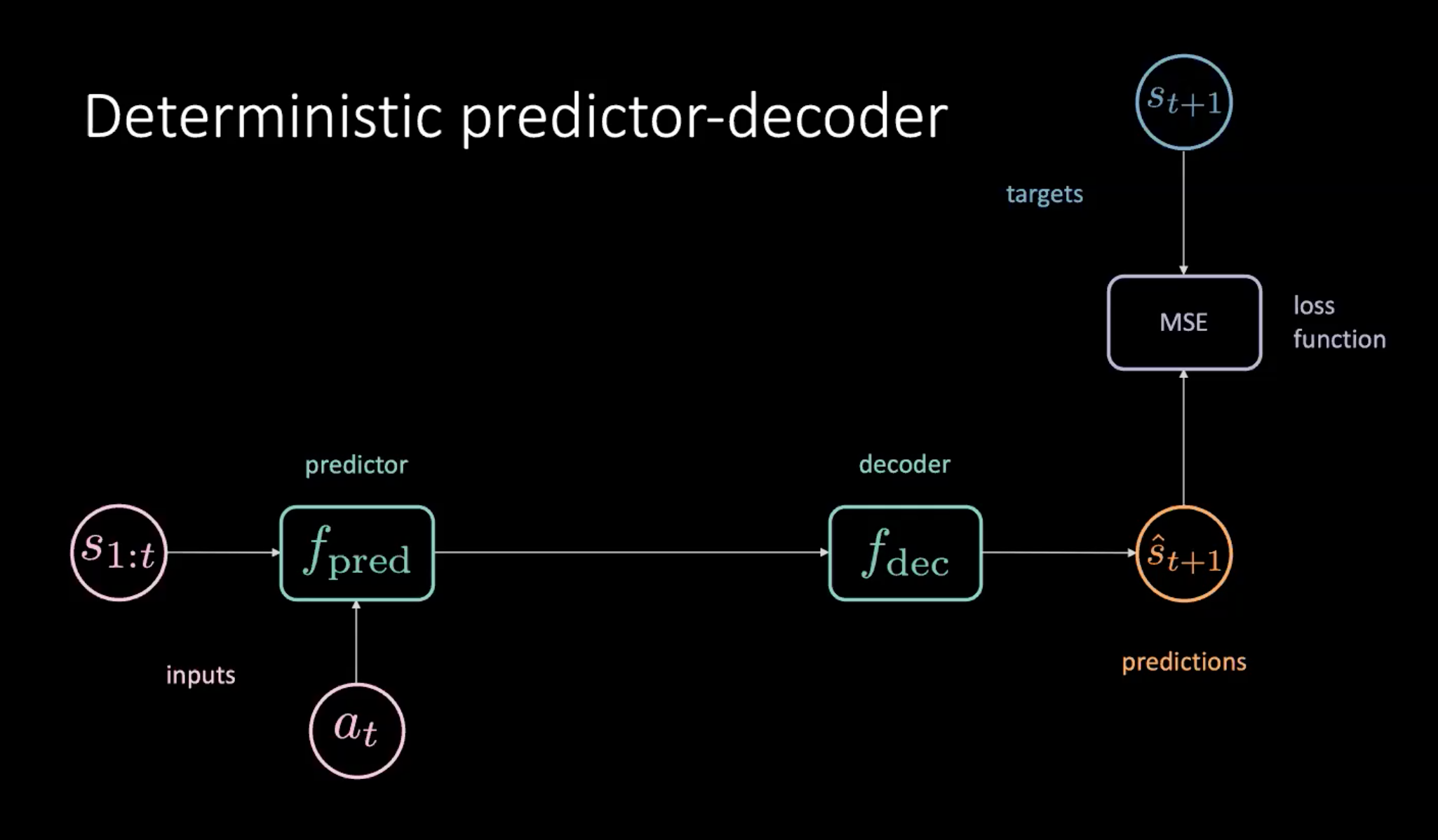
그림 8: 세계 모델 학습을 위한 결정론적 예측 변수-디코더

그림 8에 나와있듯이, 우리에게는 예측 변수 모듈에 제공되는 상태($s_{1:t}$)와 행동($a_t$)의 순서가 있다. 예측 변수는 디코더로 넘어가는 미래의 숨은 표현을 출력한다. 디코더는 미래의 숨은 표현을 디코딩하고 예측($\hat s_{t+1}$)을 출력한다. 그러면 예측값 $\hat s_{t+1}$과 $s_{t+1}$ 사이의 평균 제곱 오차^MSE 최소화를 통해 모델을 학습시킨다.

그림 9: 실제 미래 vs. 결정론적 미래

불행히도 이것은 작동하지 않는다.

우리는 결정론적 출력값이 매우 흐릿해지게 되는 것을 알고 있다. 이것은 모델이 모든 미래 가능성에 대한 평균을 내기 때문이다. 원래 놓여있던 곳의 펜이 무작위로 떨어진다는 측면에서 이것은 이전 강의들에서 언급했던 미래 복합성과 비교될 수 있다. 만약 모든 위치에 걸친 평균을 취한다면, 펜은 절대 움직이지 않았다는 잘못된 믿음을 가진다.

우리는 모델의 잠재 변수를 소개함으로써 이 문제를 추가할 수 있다.

변이 예측 신경망

이전 섹션에서 기술된 문제를 해결하기 위하여, 낮은 차원의 잠재 변수 $z_t$를 차원수를 맞추고자 확장 모듈 $f_{exp}$을 통과하는 원래 신경망에 추가한다.

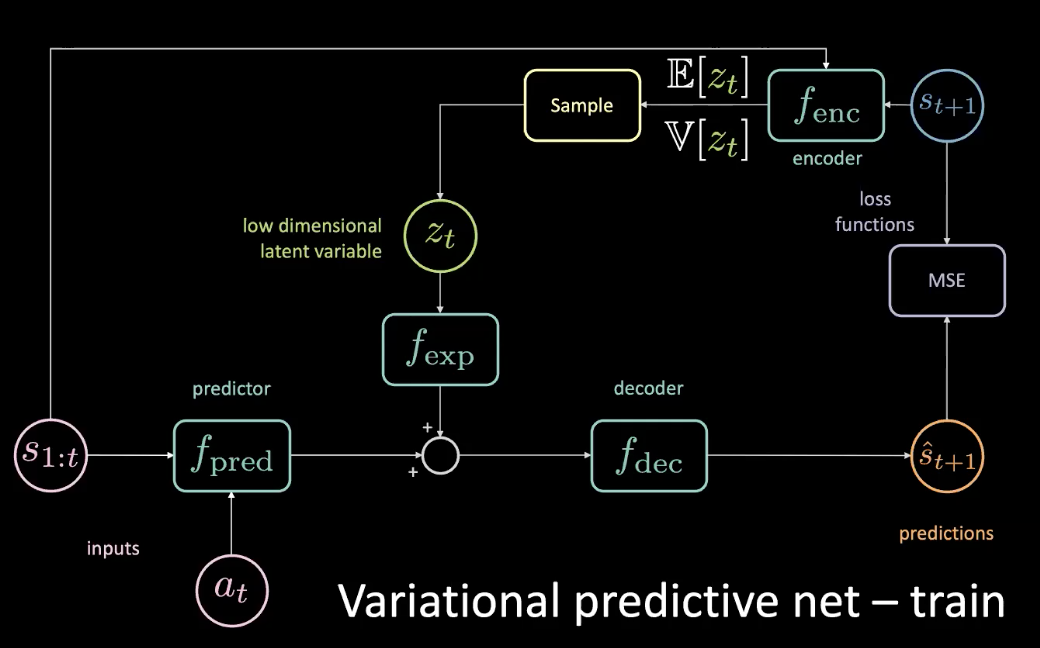
그림 10: 변이 예측 신경망 - 학습

$z_t$는 평균 제곱 오차^MSE가 구체적인 예측을 위하여 최소화되는 것처럼 선택된다. 잠재 변수 튜닝으로, 잠재 공간으로 경사 하강법을 사용해서 평균 제곱 오차를 0으로 만들 수 있다. 하지만 이 방법은 비용이 매우 많이 든다. 그래서 실제로는 인코더를 적용한 잠재 변수를 예측할 수 있는 것이다. 인코더는 미래 상태를 이용하여 $z_t$를 샘플링 할 수 있는 평균과 분산 분포를 알려준다.

학습시키는 동안, 미래 예측과 그에 따른 정보를 통해 무슨 일이 일어날지 알아낼 수 있고 그 정보는 잠재 변수를 예측하는데 사용할 수 있다. 그러나 테스트 시간 동안에는 미래에 대한 접근 권한이 없다. 이것은 Kullback-Leibler 발산^{KL divergence}을 최적화하여 가능한 한 이전에 근접한 사후분포를 주는 인코더를 적용하는 것으로 문제를 해결하면 된다.

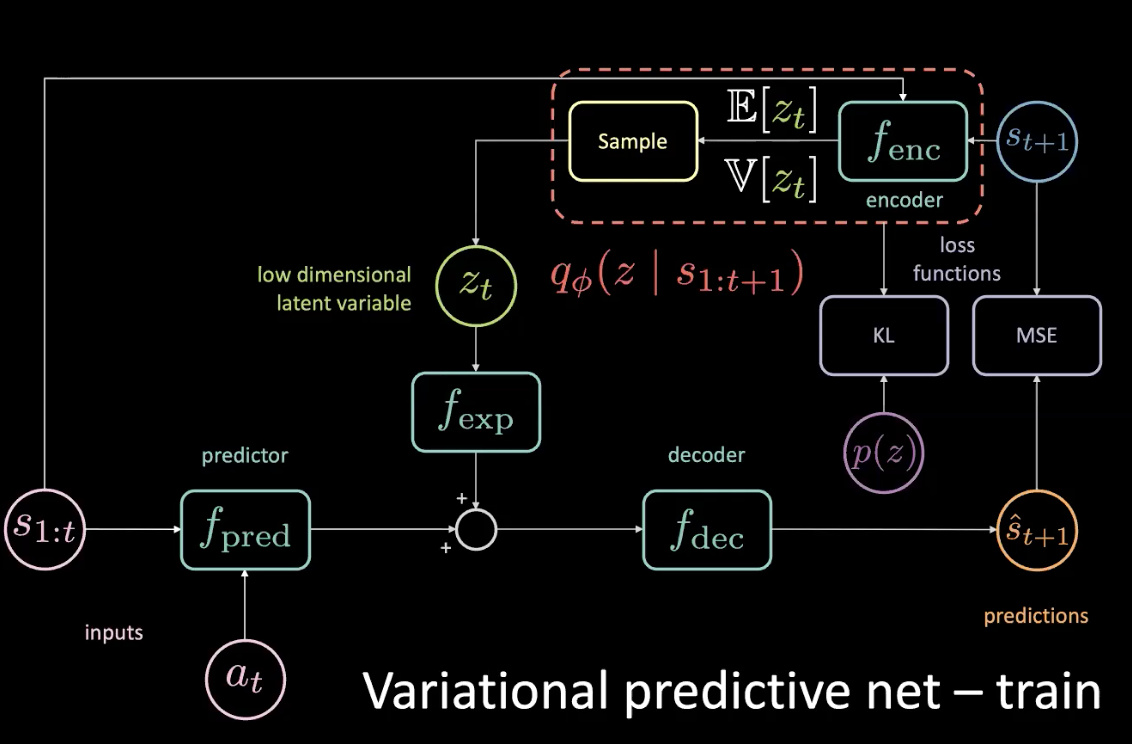
그림 11: 변이 예측 신경망 - 학습 (사전 분포 포함)

이제 추론 과정을 살펴보도록 하자 - 우리는 어떻게 운전할까?

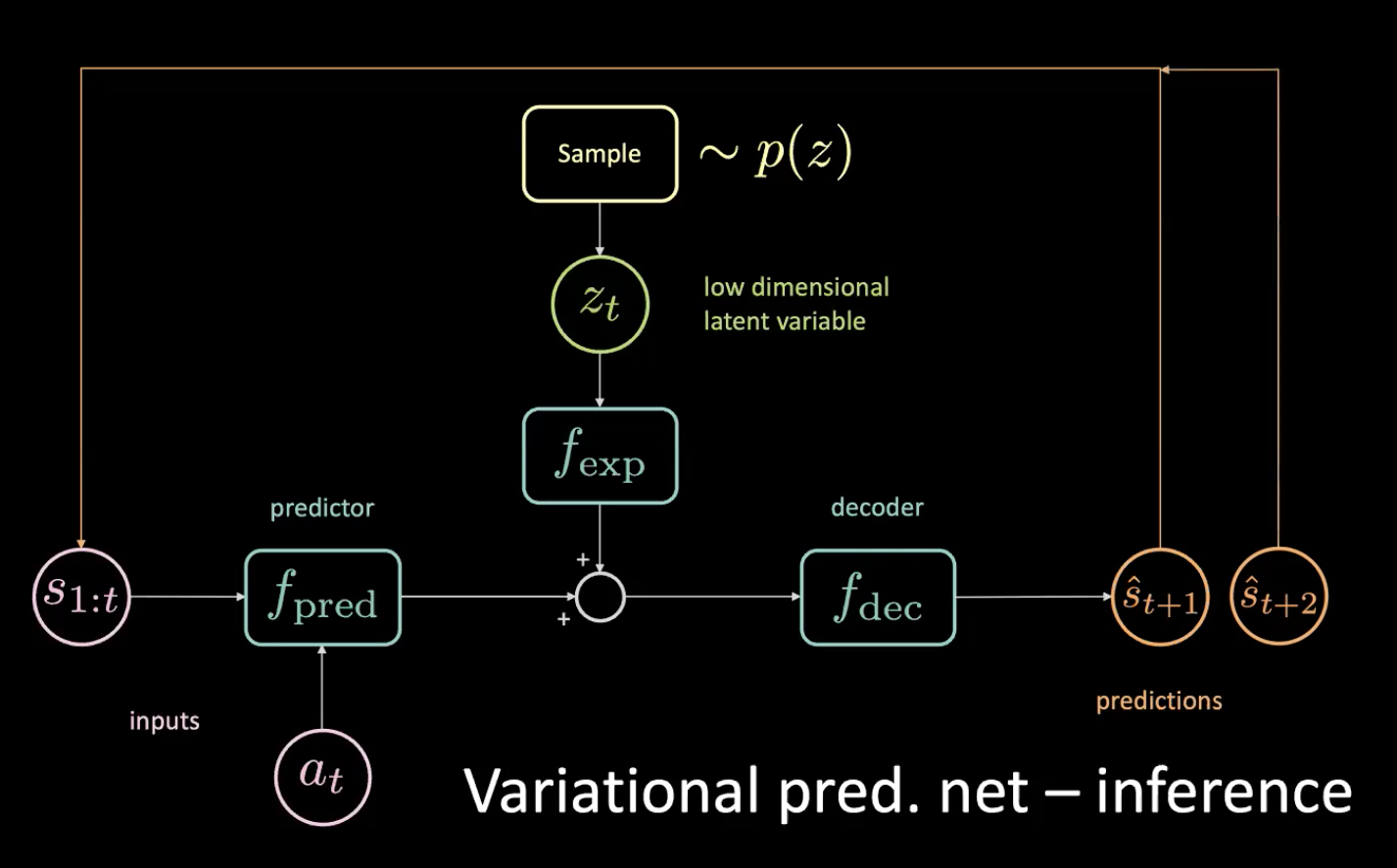
그림 12: 변이 예측 신경망 - 추론

인코더가 이 분포를 향해 쏘도록 강제하여 이전의 낮은 차원의 잠재 변수 $z_t$를 샘플링하게 된다. 예측값 $\hat s_{t+1}$을 얻은 후, 그것을 (자동 회귀 단계로) 되돌리고 다음 예측 $\hat s_{t+2}$을 얻은 후 이러한 방식으로 계속 신경망에 공급한다.

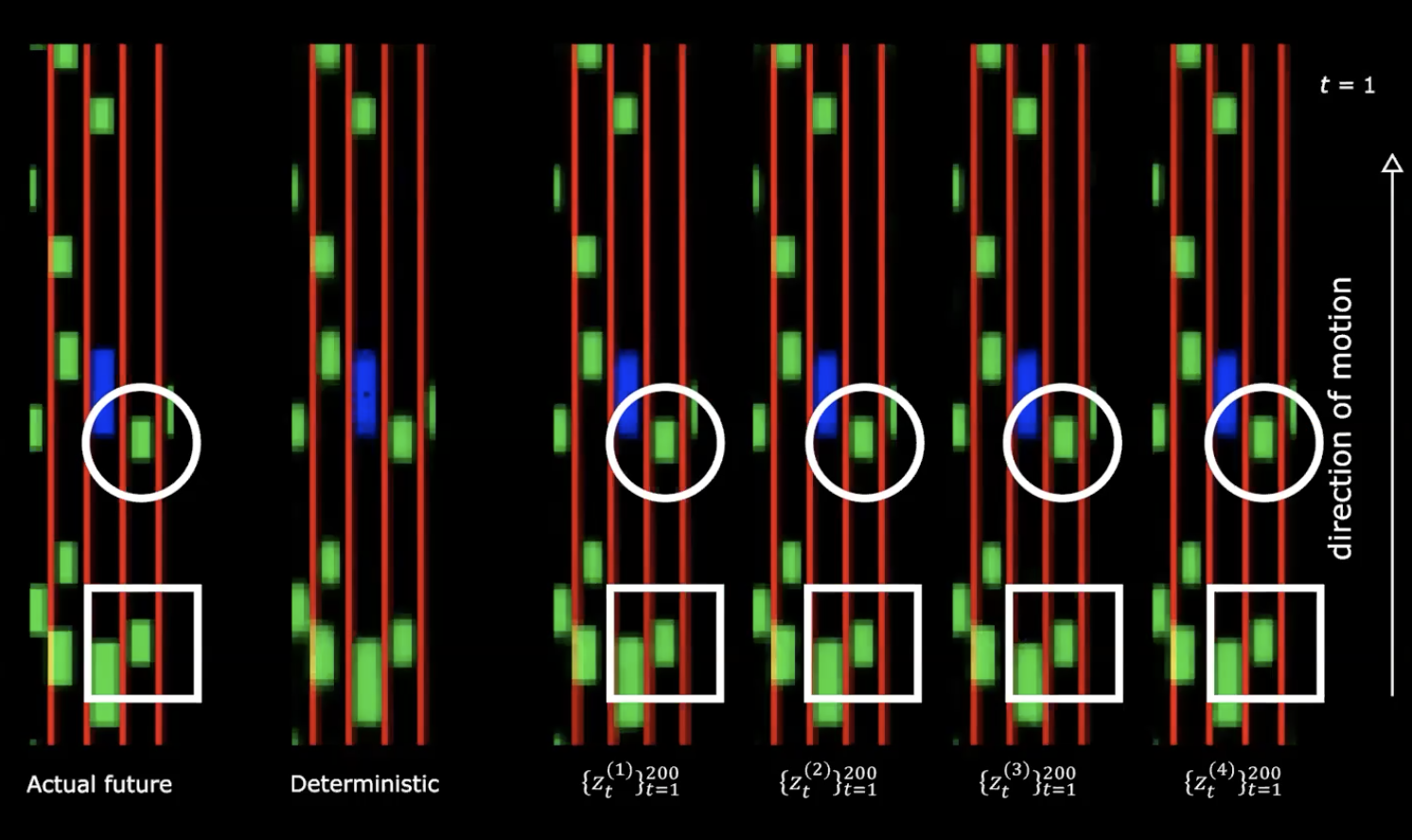
그림 13: 실제 미래 vs 결정론적

위 그림의 오른쪽 편에서 정규 분포를 나타내는 4가지 그림을 볼 수 있다. 동일한 초기 상태로 시작하고 잠재 변수에 200개의 다른 값을 제공한다.

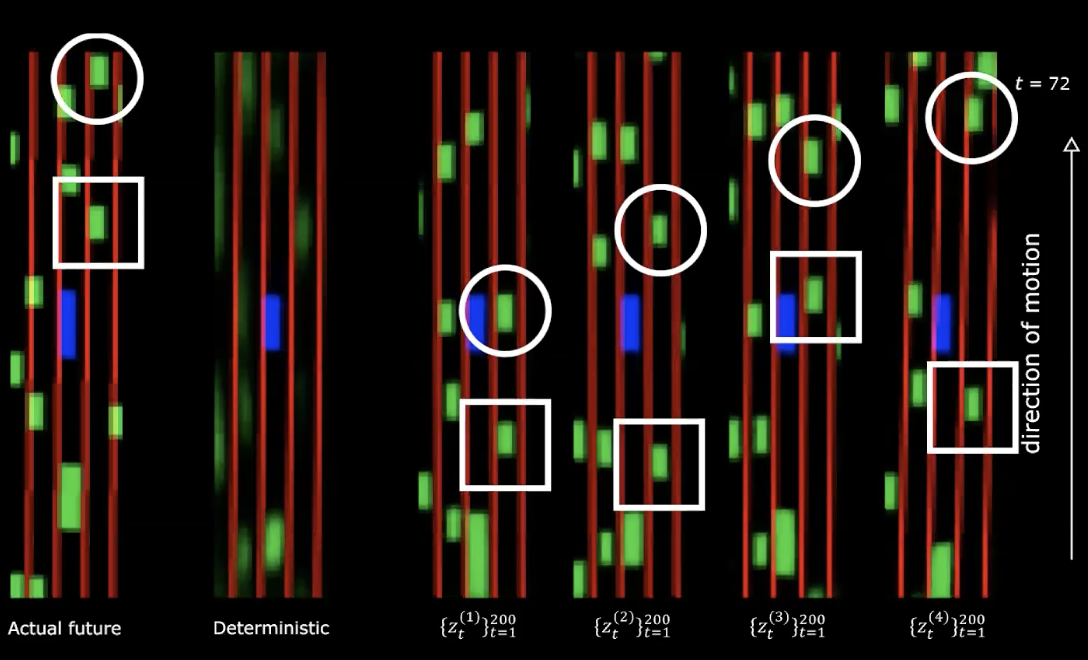
그림 14: 실제 미래 vs 결정론적 - 이동 후

우리는 여기서 다른 잠재 변수를 제공하는 것은 다른 행동에 따른 다른 순서를 생성한다는 것을 알아챌 수 있다. 즉, 미래를 만들어내는 신경망을 가지고 있다는 뜻이다. 꽤 매력적이다!

다음은 무엇일까?

이제 차선과 위 그림에 묘사된 근접 비용 최적화를 통한 정책을 학습시키기 위한 엄청난 양의 데이터를 사용할 수 있다.

이 다양한 미래는 신경망에 공급하는 잠재 변수 순서에서 온다. 경사 상승을 수행한다면 - 잠재 공간에서, 근접 비용을 올리려고 할 것이기 때문에 다른 차들이 당신을 향해 가는 것과 마찬가지로 잠재 변수 순서를 얻게 된다.

행동 무감각 & 잠재 드롭아웃

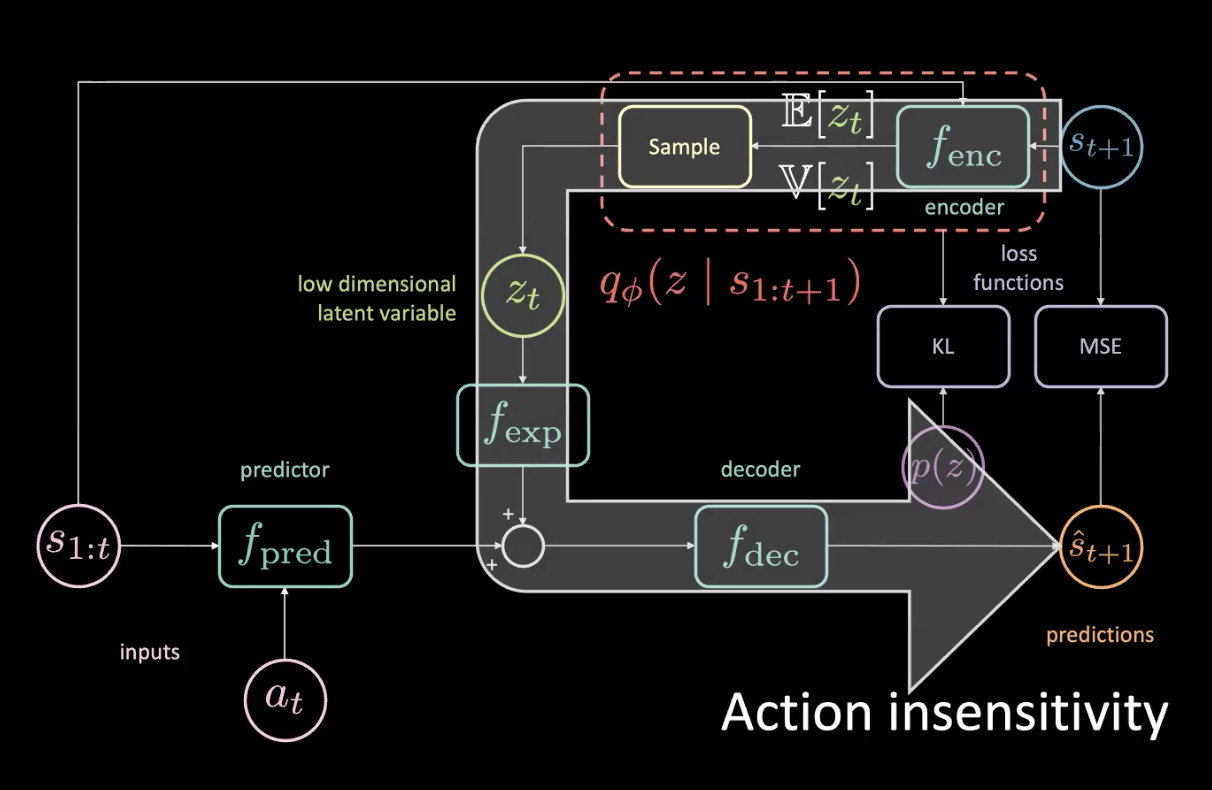
그림 15: 이슈 - 행동 무감각

실제로 미래에 접근할 수 있는 상황이 주어지고 조금이라도 왼쪽으로 틀어본다면, 모든 것이 오른쪽으로 돌 것이며 그것은 평균 제곱 오차^MSE에 매우 크게 기여할 것이다. 만약 잠재 변수가 신경망 바닥 부분에 모든 것이 우리가 원하지 않는 오른쪽으로 돌게 영향을 미칠 수 있다면 평균 제곱 오차^MSE 손실은 최적화될 수 있을 것이다.모든 것이 오른쪽으로 돌아설 때 결정론적 과제이기 때문에 말할 수 있는 것이다.

그림 15의 큰 화살표는 정보 유출을 의미하므로 예측자에 제공되는 현재 행동에 대하여 더이상 민감하지 않았다.

그림 16: 이슈 - 행동 무감각

그림 16의 가장 오른쪽 다이어그램에서 잠재 변수의 실제 순서를 갖고 (가장 정확한 미래를 얻도록 허용하는 잠재변수) 전문가에 의해 취해지는 행동의 실제 순서를 가진다. 왼쪽의 두 그림은 행동 순서를 제외한 잠재 변수를 무작위로 샘플링했으므로 스티어링을 볼 것이라 기대하게 된다. 왼쪽 아래 그림은 임의의 행동을 제외한 잠재 변수의 실제 순서를 보여주고 있고 우리는 회전이 대부분 회전과 (다른 에피소드에서 샘플링된) 행동을 인코디하는 행동이라기보다 잠재적인 것들로부터 왔다는 사실을 명확히 알 수 있다는 것이다.

이 문제를 해결하는 방법은 무엇일까?

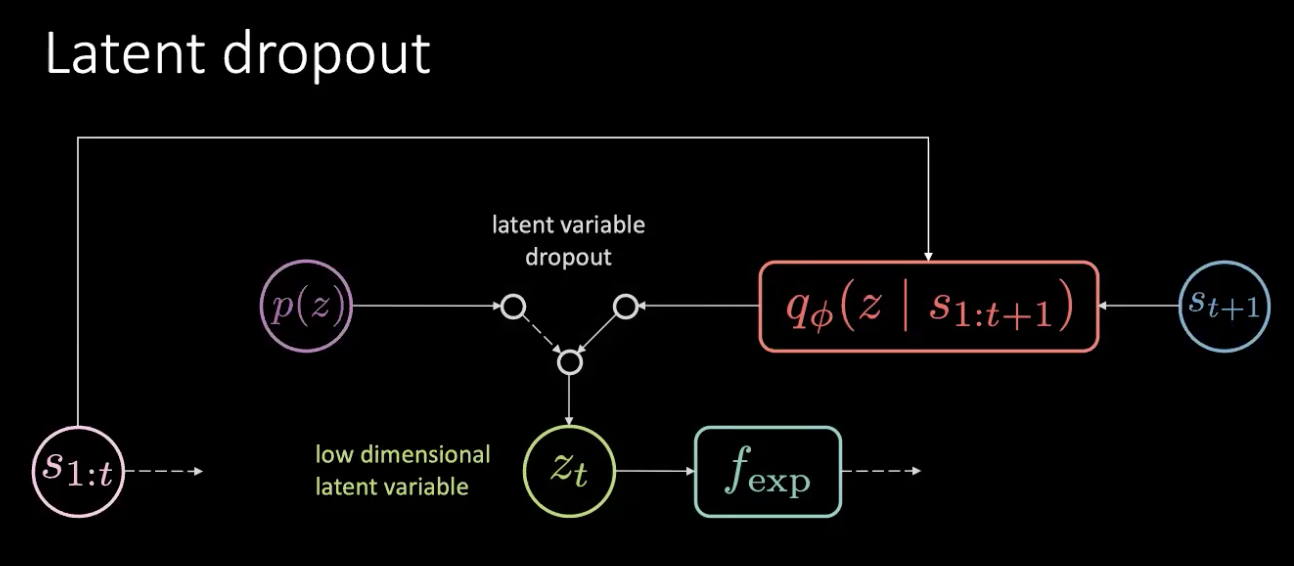
그림 17: 해결 - 잠재 드롭아웃

문제는 메모리 유출이 아니라 정보 유출이다. 이 문제를 단순히 이 잠재적인 것을 드롭아웃하고 무작위의 사전분포에서 샘플링함으로써 해결하게 된다. 우리는 인코더 ($f_{enc}$)의 출력값을 항상 믿지 않지만 이전의 것들 중 고르게 된다. 이러한 방법으로는 더 이상 잠재 변수 안에서 이루어지는 회전을 인코딩할 수 없게 된다. 또한 정보는 잠재 변수가 아닌 행동으로 인코딩된다.

그림 18: 잠재 드롭아웃 성능

오른쪽의 마지막 두 이미지에서 행동의 실제 순서를 가지는 잠재 변수의 다른 두 집합을 볼 수 있으며 이 신경망들이 잠재 드롭아웃 속임수로 학습되었다는 사실 또한 알 수 있다. 이제 회전이 더 이상 잠재 변수가 아니라 행동에 의해 인코딩되는 것을 알 수 있다.

에이전트 학습

이전 섹션에서 우리는 현실 세계 경험 시뮬레이션에 의한 세계 모델을 얻을 수 있는 방법을 살펴보았다. 이번에는 이 세계 모델을 우리가 가진 에이전트를 학습시키는데 사용할 것이다. 목표는 이전의 이력이 주어진 상태로 행동하도록 하는 정책을 배우는 것이다. 상태 $s_t$(속도, 위치와 컨텍스트 이미지)가 주어진 상태에서 에이전트는 행동 $a_t$(가속, 제동과 핸들 조작)를 취하고, 세계 모델은 다음 상태, ‘근접 비용-차선 비용’으로 이루어진 $(s_t, a_t)$와 연관된 비용을 출력하게 된다.

애매한 예측을 피하고자 논의되었던 이전 섹션에서 미래 상태 $s_{t+1}$의 인코더 모듈이나 사전 분포 $P(z)$로부터 잠재 변수 $z_t$를 샘플링해야 한다. 세계 모델은 다음 상태 $\hat s_{t+1}$와 비용을 예측하기 위하여 이전 상태 $s_{1:t}$, 에이전트에 의해 이루어지는 행동 그리고 잠재 변수 $z_t$를 얻는다. 이것은 최종 예측과 최적화를 위한 손실을 제공하고자 여러번 복제되는 하나의 모듈로 구성된다.(그림 19)

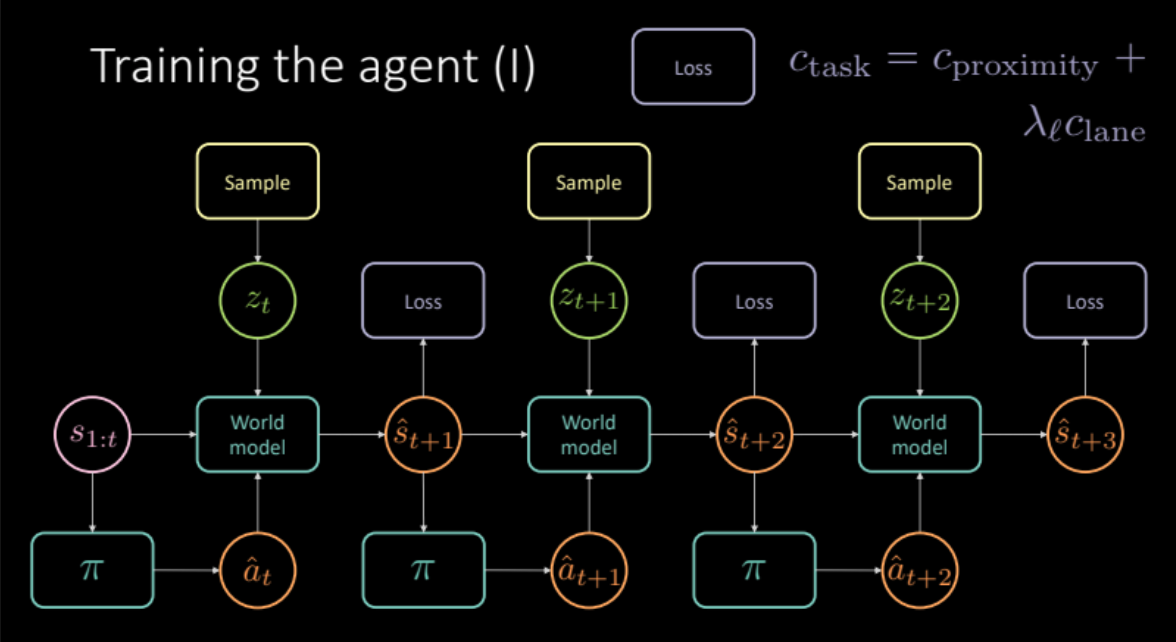
그림 19: 각 작업의 모델 아키텍처

이제 모델이 준비되었으니 어떻게 생겼는지 살펴보자!!

그림 20: 학습된 정책: 충돌하거나 길에서 멀어지는 에이전트

불행히도 이것은 작동하지 않는다. 이러한 방식으로 학습된 정책은 비용이 전혀 들지 않기 때문에 어두운 예측을 배우는 것이므로 유용하지 않다.

이 이슈를 어떻게 잘 다룰 수 있을까? 예측을 개선하고자 다른 차량을 흉내내는 것을 시도할 수 있을까?

전문가 흉내내기

전문가인 것처럼 흉내내려면 어떻게 할까? 우리는 실제 미래에 가장 근접한 상태로부터 특정한 행동을 하고 난 이후의 모델 예측을 원한다. 이것은 학습을 위한 전문 규제화 도구로서 행동한다. 비용 함수는 이제 각 작업에 따른 정확한 비용(근접 비용과 차선 비용)과 이 전문 규제화 기간 모두를 포함한다. 또한 실제 미래를 고려한 손실을 계산함으로써 모델에서 잠재 변수를 제거해야 하는데 잠재 변수는 특정 예측을 알려주지만 만약 평균 예측에 따라 움직인다면 이 설정이 더 낫기 때문이다.

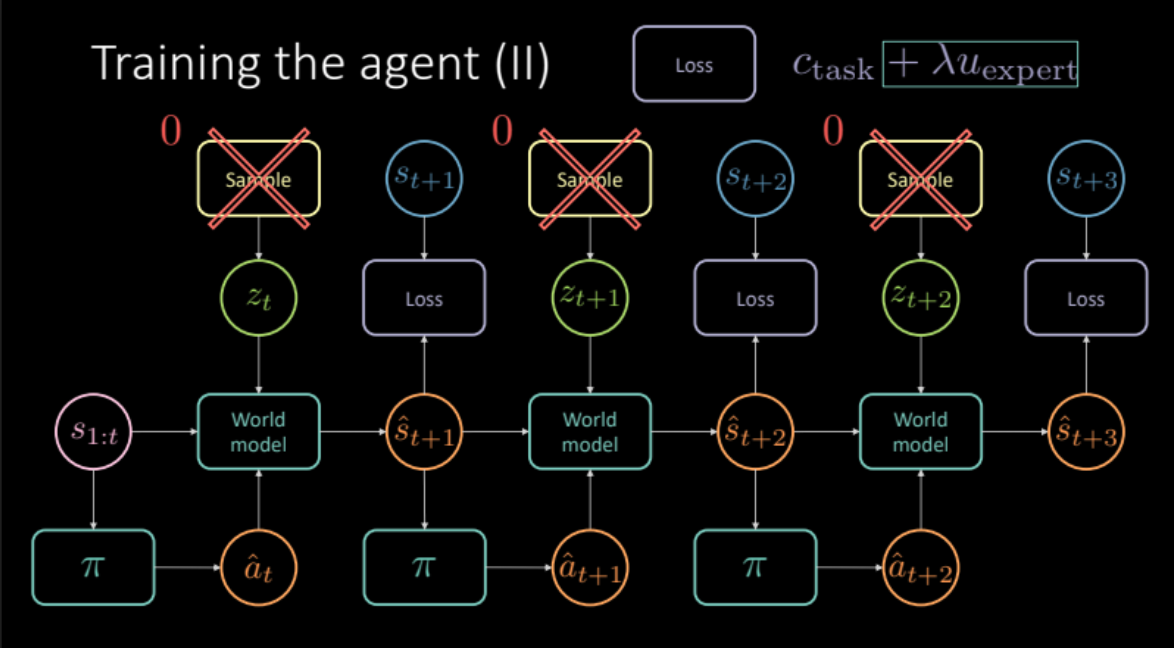
그림 21: 전문 규제화 기반 모델 아키텍처

그래서 이 모델은 어떻게 작업을 수행할까?

그림 22: 전문가 흉내로 학습한 정책

위 그림에서 볼 수 있듯이, 모델은 실제로 믿을 수 없을 정도로 잘 작동하고 매우 좋은 예측 결과를 만들기 위해 학습한다. 이것은 모델 기반 모사 학습이었으며, 다른 것들을 흉내내려고 하는 에이전트를 모델링하고자 노력했다.

그런데 더 잘할 수 있을까?

단지 끝에서 제거하려고 변이 오토인코더를 학습시켰던 것일까?

만약 모델 예측 지향의 불확실성을 최소화하는 것을 기대한다면 여전히 개선할 수 있다고 밝히는 바이다.

모델 불확실성 지향 최소화

모델 불확실성 지향을 최소화하는 것은 어떤 의미이며 어떻게 할 것인가? 이 물음에 답하기 전, 3주차 실습에서 살펴보았던 것을 상기해보자.

동일한 데이터에 대하여 여러 모델을 학습시키면, 그 모든 모델들은 (빨간색으로 표시된) 결과적으로 학습 지역 분산이 0인 학습 지역의 지점들에 도달하게 된다. 하지만 학습 지역에서 더 멀어지면서, 이 모델들에 대한 손실 함수의 궤적은 발산하기 시작하고 분산은 증가한다. 이것은 그림 23에 나와 있다. 그렇지만 분산은 미분가능함으로써 이를 최소화하기 위한 경사 하강을 실행할 수 있다.

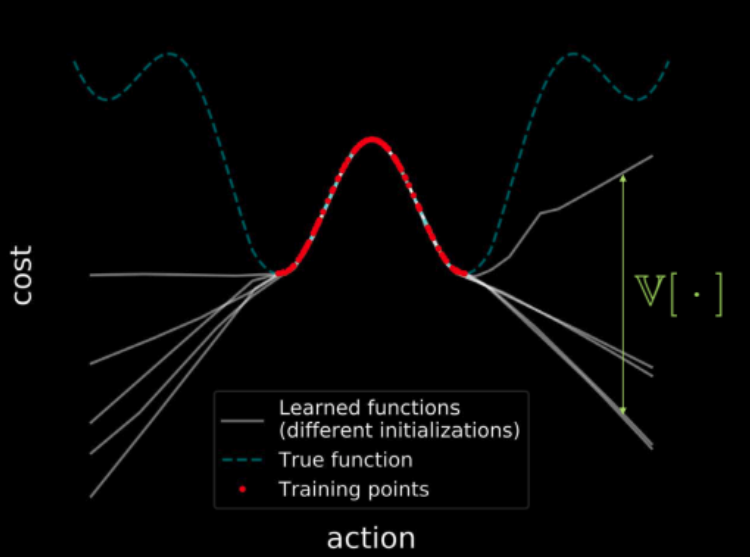
그림 23: 전체 입력 공간에 걸친 비용 시각화

본론으로 돌아와서, 우리는 오직 관찰 가능한 데이터 적용에 따른 정책 학습이 어렵다는 것을 보는데 상태 분포가 실행 단계에서 학습 단계 동안 관찰된 것과 다를 수 있기 때문이다. 세계 모델은 임의의 예측을 낮은 비용이라는 잘못된 결과를 만들 수도 있는 학습 도메인 밖으로 보낼 수 있다는 것이다. 그러면 정책 신경망은 역학 모델에서 이러한 오류들을 이용하고 잘못된 최적화 상태로 이어지는 행동을 할 수 있다.

이를 해결하고자 예측에 따른 역학 모델의 불확실성을 측정하는 추가 비용을 제안하는 바이다. 이것은 동일한 입력값과 각각의 다른 드롭아웃 마스크 그리고 다른 출력값에 걸친 분산을 계산하는 것으로 계산이 가능하다. 이는 정책 신경망이 오직 순방향 모델이 확실한 데 따른 행동을 하도록 받쳐준다.

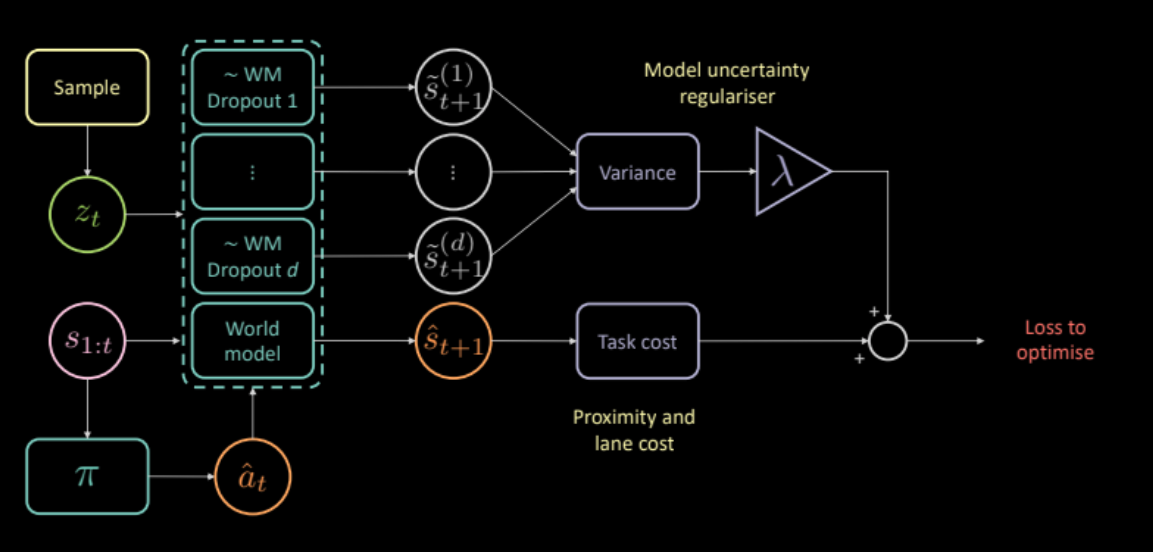
그림 24: 불확실성 규제 도구 기반 모델 아키텍처

그래서 불확실성 규제 도구가 더 나은 정책을 학습할 수 있도록 도와주는 것일까?

그렇다. 이러한 방식으로 학습한 정책은 이전 모델들보다 더 낫다.

그림 25: 불확실성 규제 도구에 근거한 정책 학습

평가

그림 26은 우리 에이전트가 교통량이 많은 상황에서 운전하는 것을 얼마나 잘 학습했는지 보여준다. 노란색 차는 순수 운전자이며, 파란색 차는 학습 에이전트 그리고 모든 녹색 차들은 가려져 있다(제어 불가능 상태이다).

그림 26: 불확실성 규제 도구로 학습한 모델 성능