The Truck Backer-Upper

셋업

우리가 해볼 작업의 목표는 트럭이 임의의 초기 위치에서 loading dock(짐 싣는 곳)으로 돌아가는 동안, 트럭의 운전을 제어하는 자기 학습 컨트롤러를 구축하는 것입니다.

아래 그림 1과 같이 후진만 허용됩니다.

Fig. 1: 트럭, 트레일러 그리고 Loading Dock

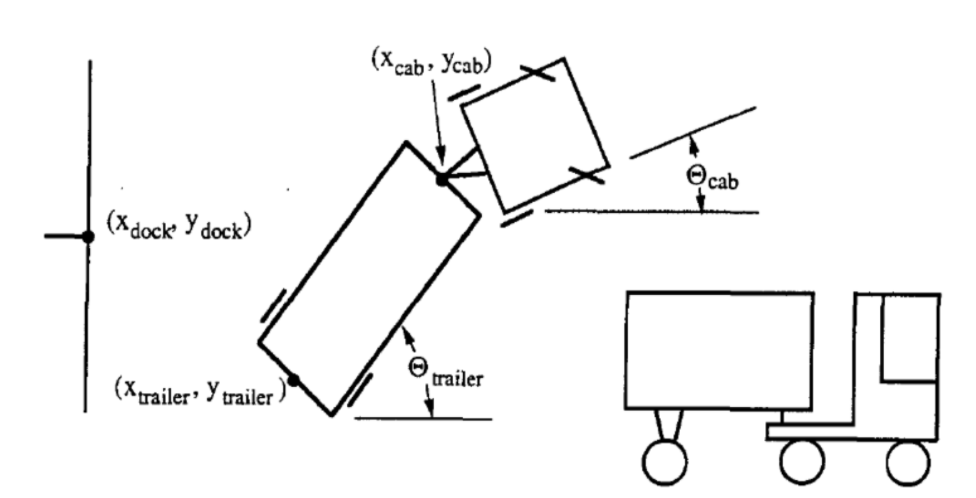트럭의 상태는 6가지 매개변수로 표현됩니다.

• $\tcab$: 트럭의 각도
• $\xcab, \ycab$: yoke의 좌표 (또는 트레일러의 앞).
• $\ttrailer$: 트레일러의 각도
• $\xtrailer, \ytrailer$: 트레일러 뒷면의 좌표

컨트롤러의 목표는 매 시간 $k$ 때마다 적절한 각도 $\phi$를 선택하는 것입니다. 이때 트럭은 고정 된 작은 거리에서 후진합니다. 성공은 다음 두 가지 기준에 따라 달라집니다.

1. 트레일러의 뒷면은 loading dock의 벽과 평행합니다. e.g. $\ttrailer = 0$.
2. 트레일러의 뒷면 ($\xtrailer, \ytrailer$)은 위와 같이 지점 ($x_{dock}, y_{dock}$)에 최대한 가까워야합니다.

많은 매개변수와 시각화

Fig. 2: 시각화를 위한 매개변수들

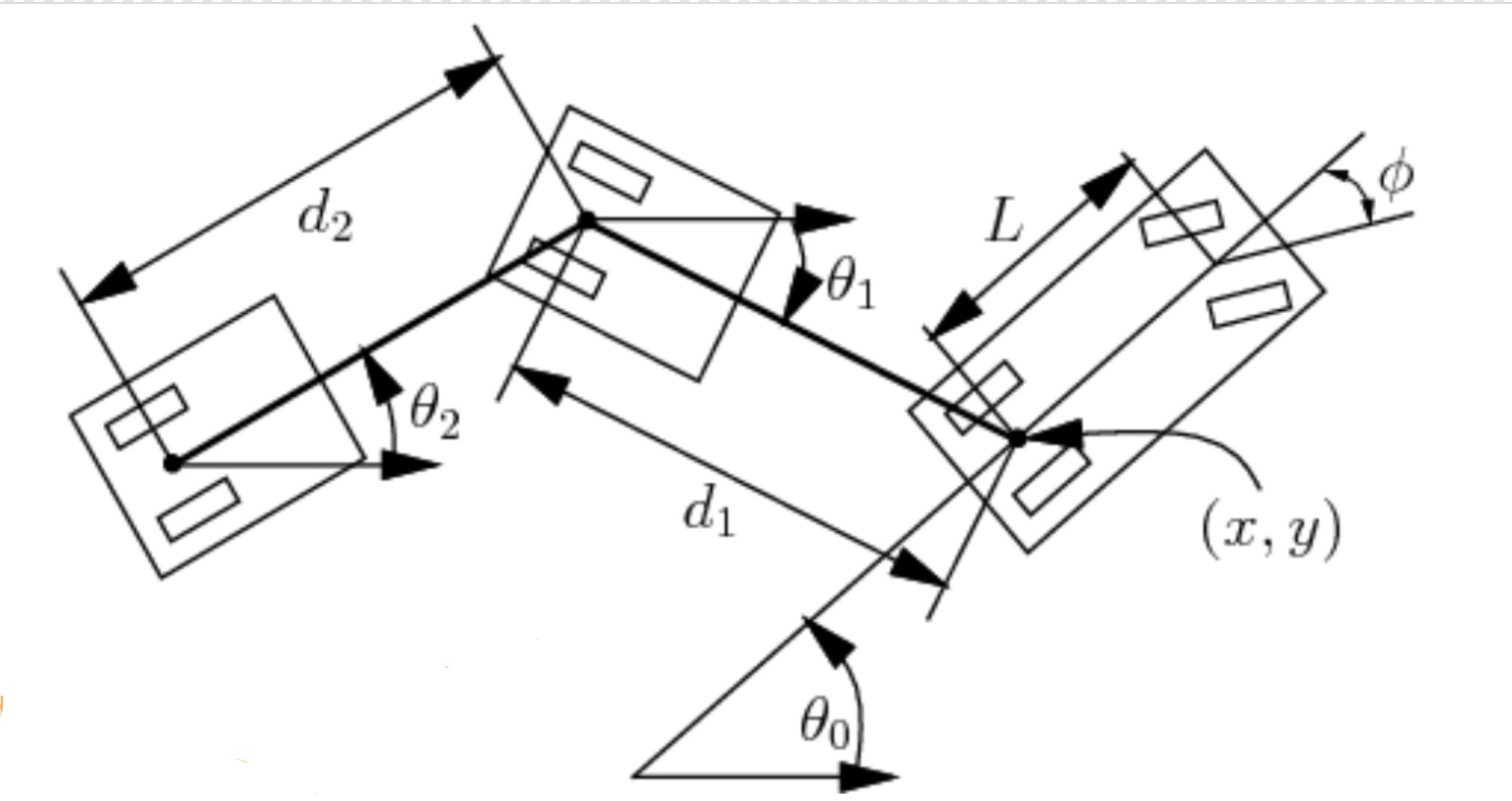이 섹션에서는 그림 2에 표시된 몇 가지 추가 매개 변수도 고려합니다. 주어진 자동차 길이 $L$, 자동차와 트레일러 사이의 거리 $d_1$ 그리고 트레일러 길이 $d_2$ 등이 주어지면, 각도와 위치의 변화를 계산할 수 있습니다.

여기서 $s$는 속도^{signed speed}를 나타내고 $\phi$는 음의 운전^steering 각도를 나타냅니다. 이제 $\xcab$, $\ycab$, $\theta_0$ 그리고 $\theta_1$ 네 가지 매개 변수만으로 상태를 나타낼 수 있습니다. 길이 매개 변수가 알려져 있고 $\xtrailer, \ytrailer$가 $\xcab, \ycab, d_1, \theta_1$.에 의해 결정되기 때문입니다.

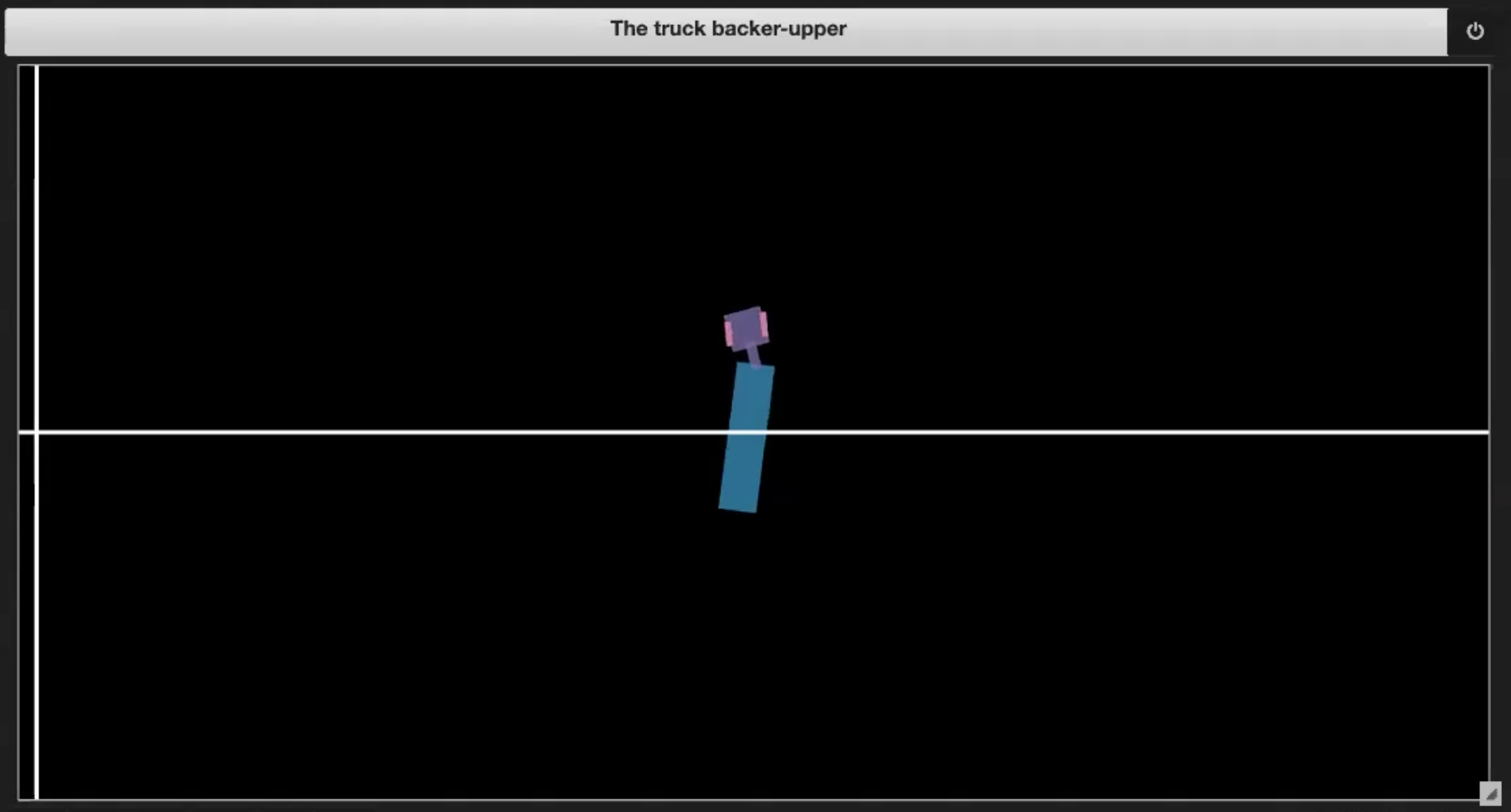
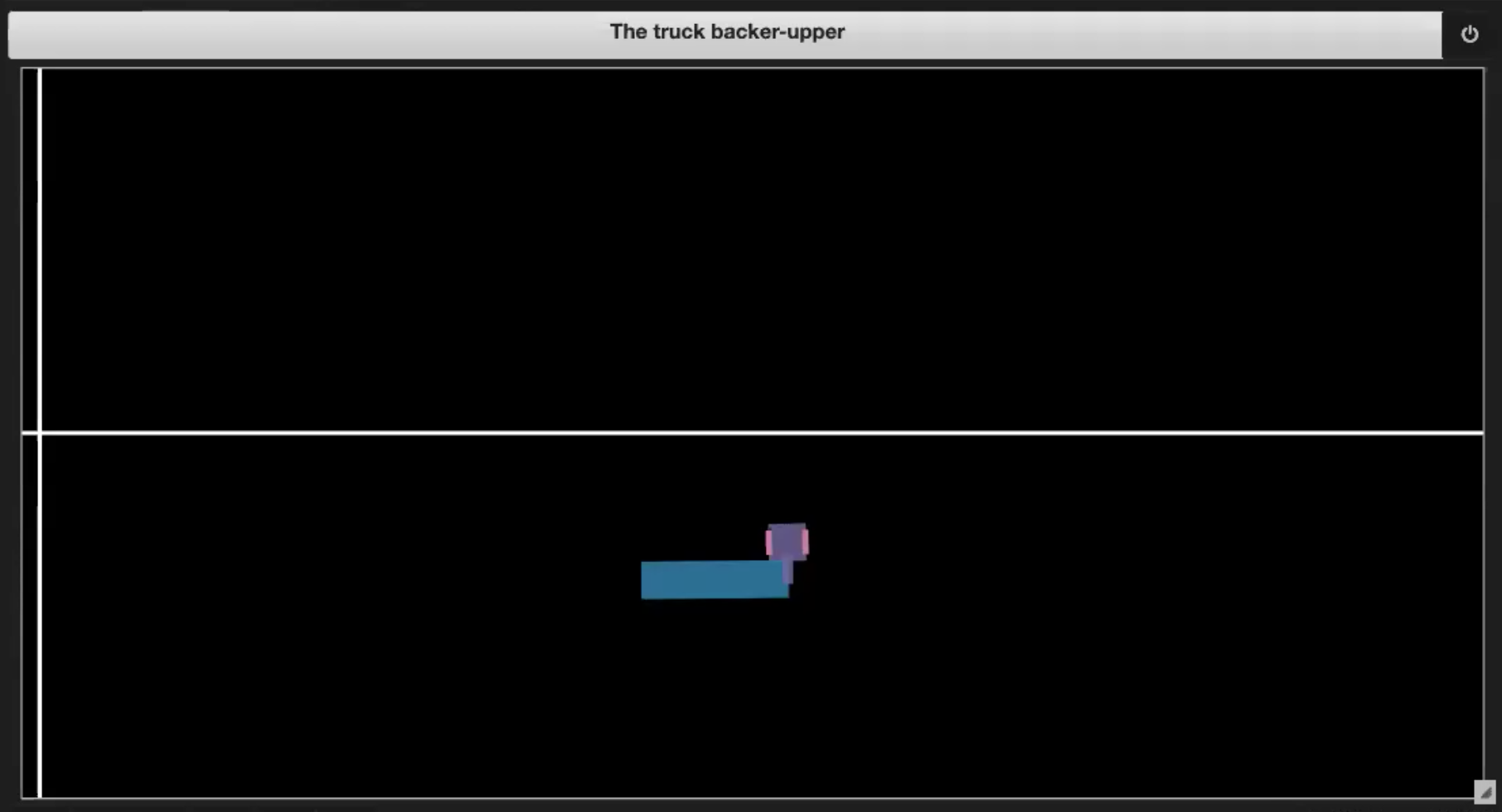
Deep Learning 레파지토리의 Jupyter Notebook에는 그림 3 (1-4)에 표현되어 있는 몇 가지 샘플 환경이 있습니다.

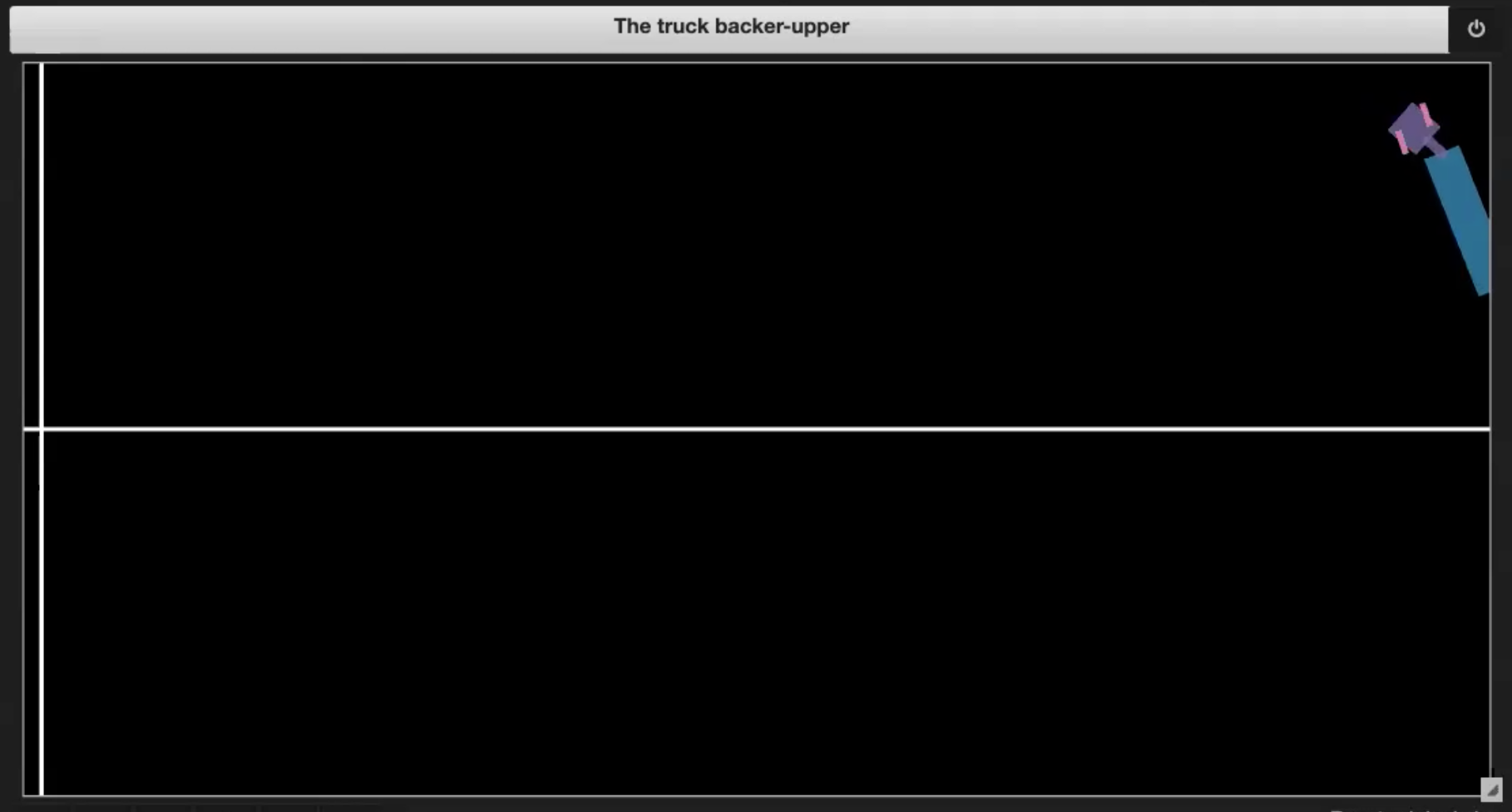
Fig. 3.1: 환경에 대한 샘플 플롯	Fig. 3.2: 스스로 운전하기 (잭 나이프)
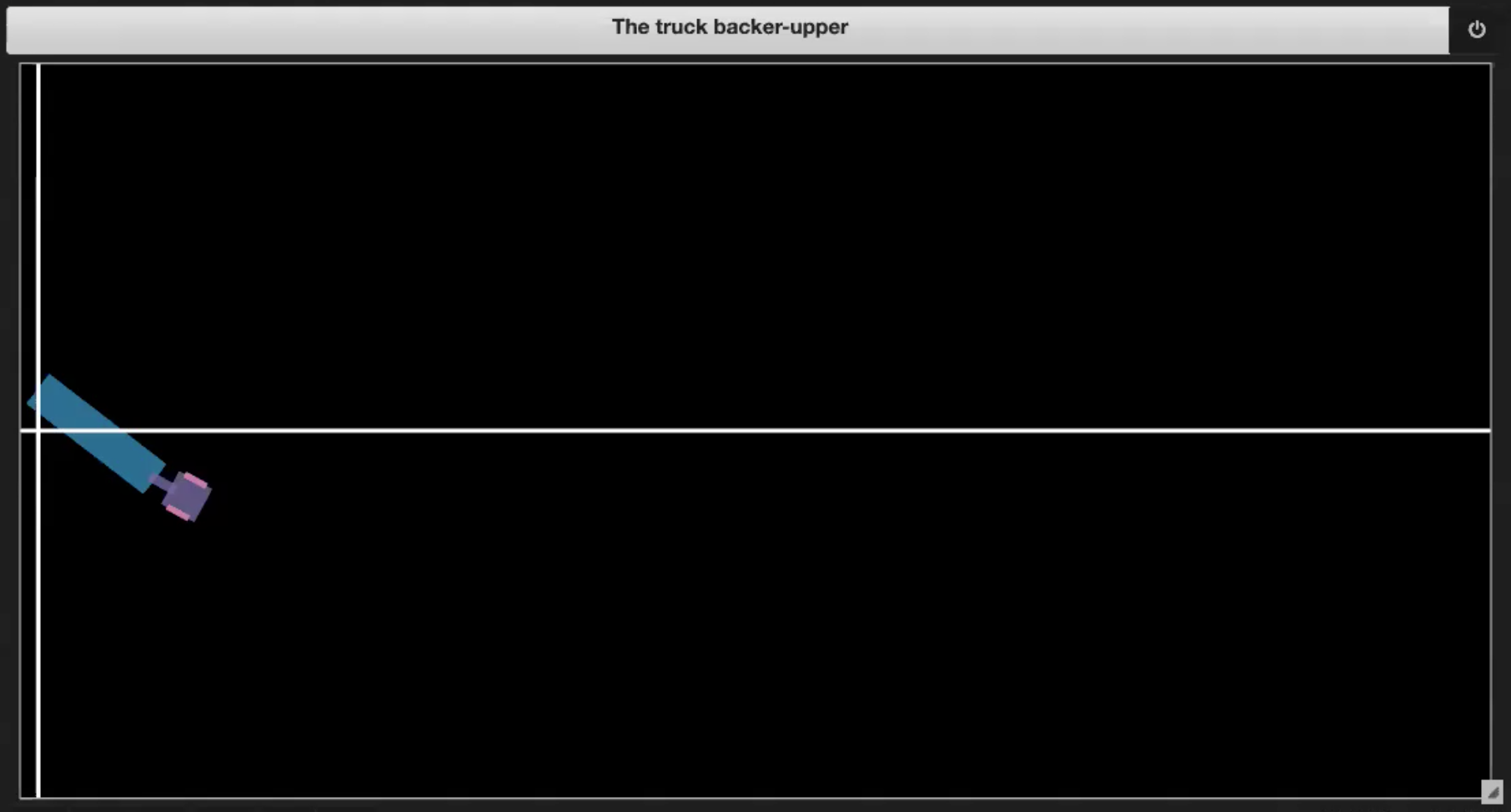Fig. 3.3: 경계를 벗어나기	Fig. 3.4: dock에 도달

매 $k$ 단계마다, $-\frac{\pi}{4}$에서 $\frac{\pi}{4}$사이의 운전 신호가 입력되고 트럭은 해당 각도를 사용하여 후진합니다.

시퀀스가 끝날 수있는 몇 가지 상황이 있습니다.

• 트럭이 스스로 운전하는 경우 (그림 3.2에서와 같이 잭나이프)
• 트럭이 경계를 벗어나는 경우 (그림 3.3 참조)
• 트럭이 dock에 도착한 경우 (그림 3.4 참조)

학습

훈련 과정은 두가지로 구성됩니다. (1) 트럭 및 트레일러 kinematics의 에뮬레이터가 될 신경망 훈련과 (2) 트럭을 제어하기위한 신경망 컨트롤러 훈련의 두 단계로 구성됩니다.

Fig. 4: 개요 다이어그램

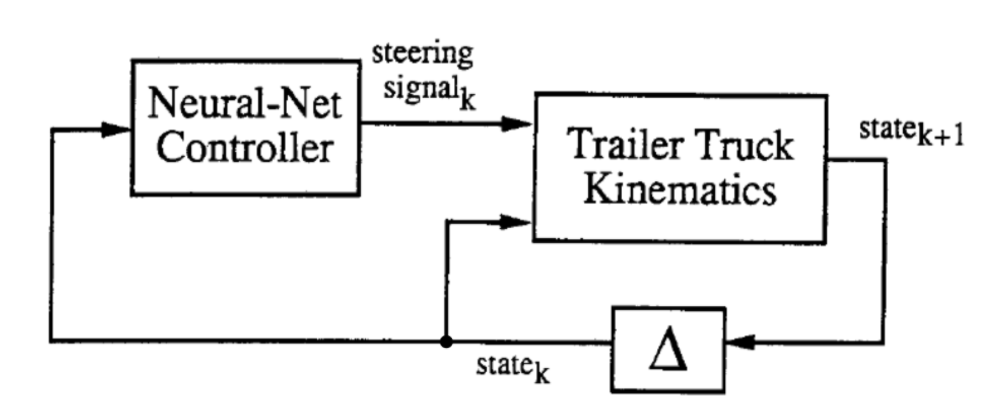위 추상도에서, 두 블록은 훈련 될 두 네트워크입니다. $k$ 단계마다 “Trailer Truck Kinematics” 또는 우리가 에뮬레이터라고 부르는 것은 컨트롤러에서 생성 된 6차원의 상태 벡터와 운전 신호^{steering signal}를 가져 와서 $k+1$ 단계의 새로운 6 차원 상태 벡터를 생성합니다.

에뮬레이터

에뮬레이터는 현재 위치 ($\tcab^t$,$\xcab^t, \ycab^t$, $\ttrailer^t$, $\xtrailer^t$, $\ytrailer^t$)와 운전 방향 $\phi^t$를 input으로 받습니다. 그리고 다음 타입 스탭의 상태를 output으로 출력합니다($\tcab^{t+1}$,$\xcab^{t+1}, \ycab^{t+1}$, $\ttrailer^{t+1}$, $\xtrailer^{t+1}$, $\ytrailer^{t+1}$). 이 신경망은 ReLu 활성화 함수를 가지는 선형 은닉 계층과 선형 출력 계층으로 구성됩니다. 손실 함수로 MSE를 사용하고 확률적 경사 하강법을 통해 에뮬레이터를 훈련합니다.

Fig. 5: 신경망 에뮬레이터 학습

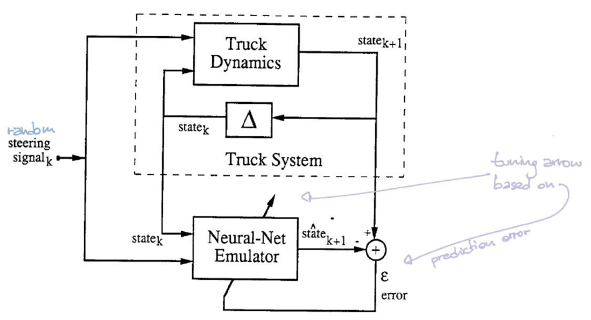이 설정에서 시뮬레이터는 현재 위치와 운전 각도를 고려하여 다음 단계의 위치를 알려줄 수 있습니다. 따라서 시뮬레이터를 에뮬레이트하는 신경망이 실제로 필요하지 않습니다. 그러나 더 복잡한 시스템에서는 주어진 시스템에 해당하는 방정식에 접근하지 못할 수 있습니다. 즉 우리는 좋은 계산 가능한 형식의 보편적인 법칙을 가지고 있지 않습니다. 운전 신호의 순서와 해당 경로를 기록하는 데이터만 관찰 할 수 있습니다. 이 경우 복잡한 시스템의 역학^dynamic을 모방하기 위해 신경망을 훈련시켜야합니다.

에뮬레이터를 훈련시키기 위해, 우리가 에뮬레이터를 훈련시킬 때 살펴 봐야 할 두 가지 중요한 함수가 Class truck에 있습니다.

첫 번째는 계산 후 트럭의 출력 상태를 제공하는 ‘step’ 함수입니다.

def step(self, ϕ=0, dt=1):

    # Check for illegal conditions
    if self.is_jackknifed():
        print('The truck is jackknifed!')
        return

    if self.is_offscreen():
        print('The car or trailer is off screen')
        return

    self.ϕ = ϕ
    x, y, W, L, d, s, θ0, θ1, ϕ = self._get_atributes()

    # Perform state update
    self.x += s * cos(θ0) * dt
    self.y += s * sin(θ0) * dt
    self.θ0 += s / L * tan(ϕ) * dt
    self.θ1 += s / d * sin(θ0 - θ1) * dt

두 번째는 트럭의 현재 상태를 알려주는 ‘상태’함수입니다.

def state(self):
        return (self.x, self.y, self.θ0, *self._traler_xy(), self.θ1)

먼저 두 개의 리스트을 생성합니다. 무작위로 생성 된 운전 각도 ^{steering angle} ϕ와 truck.state()를 실행하여 트럭에서 오는 초기 상태를 추가하여 입력 리스트을 생성합니다. 그리고truck.step(ϕ)으로 계산할 수있는 트럭의 출력 상태가 추가 된 출력 리스트를 생성합니다.

이제 에뮬레이터를 학습시킬 수 있습니다.

cnt = 0
for i in torch.randperm(len(train_inputs)):
    ϕ_state = train_inputs[i]
    next_state_prediction = emulator(ϕ_state)

    next_state = train_outputs[i]
    loss = criterion(next_state_prediction, next_state)

    optimiser_e.zero_grad()
    loss.backward()
    optimiser_e.step()

    if cnt == 0 or (cnt + 1) % 1000 == 0:
        print(f'{cnt + 1:4d} / {len(train_inputs)}, {loss.item():.10f}')
    cnt += 1

torch.randperm(len(train_inputs))은 $0$부터 학습 입력 길이에 $1$을 뺀 범위 내에서, 임의의 인덱스 순열을 제공합니다. 인덱스의 순열 다음으로, 시간대에서 입력 리스트의 i번째 인덱스에서 ‘ϕ_state’가 선택 될 때마다. 선형 출력 레이어가 있는 에뮬레이터 함수에 ϕ_state를 입력하고 next_state_prediction을 얻습니다. 에뮬레이터는 아래와 같이 정의 된 신경 네트워크입니다.

emulator = nn.Sequential(
    nn.Linear(steering_size + state_size, hidden_units_e),
    nn.ReLU(),
    nn.Linear(hidden_units_e, state_size)
)

여기서 우리는 MSE를 사용하여 실제 다음 상태와 예측된 다음 상태 사이의 손실을 계산합니다. 여기서 실제 다음 상태는 입력 리스트에서 ϕ_state 인덱스에 해당하는 인덱스 i가 있는 출력 리스트에서 나옵니다.

컨트롤러

그림 5를 참고한다면, $\matr{C}$ 블록은 컨트롤러를 나타냅니다. 현재 상태를 가져와 운전 각도를 출력합니다. 그런 다음 블록 $\matr{T}$(에뮬레이터)는 상태와 각도를 모두 가져와 다음 상태를 생성합니다.

Fig. 5: 상태변화 흐름 다이어그램

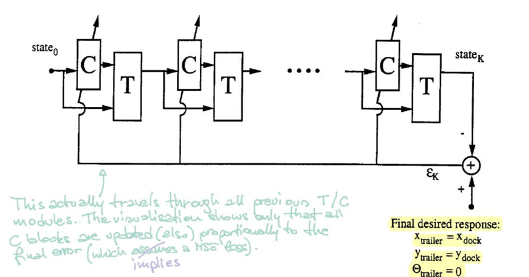컨트롤러를 훈련시키기 위해, 무작위 초기 상태에서 시작하여 트레일러가 dock와 평행이 될 때까지 특정 절차($\matr{C}$ and $\matr{T}$)를 반복합니다. 오류는 트레일러 위치와 dock 위치를 비교하여 계산됩니다. 그런 다음 역전파를 사용하여 그라디언트를 찾고 SGD를 통해 컨트롤러의 매개 변수를 업데이트합니다.

구체적인 모델 구조

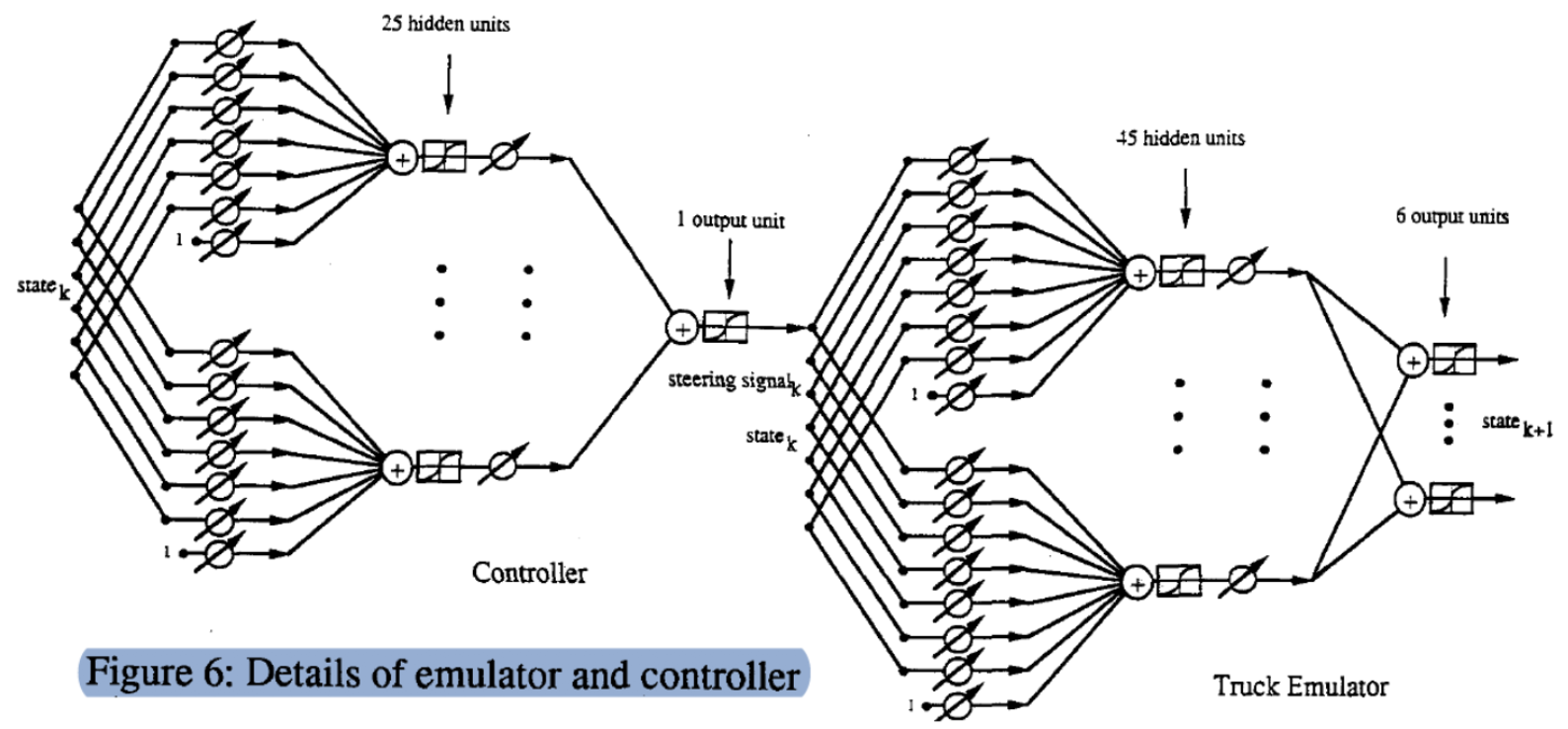
($\matr{C}$, $\matr{T}$)프로세스의 상세한 그래프입니다. 상태(6 차원 벡터)로 시작하여 조정 가능한 가중치 행렬을 곱하고 25 개의 은닉 유닛^{hidden units}을 얻습니다. 그런 다음 다른 조정 가능한 가중치 벡터를 통해 출력 (운전 신호)을 얻습니다. 마찬가지로 두 개의 레이어를 통해 상태와 각도 $\phi$ (7 dimension vector)를 입력하여 다음 단계의 상태를 생성합니다.

명확하게 확인하기 위해, 에뮬레이터의 정확한 구현을 봅시다.

state_size = 6
steering_size = 1
hidden_units_e = 45

emulator = nn.Sequential(
    nn.Linear(steering_size + state_size, hidden_units_e),
    nn.ReLU(),
    nn.Linear(hidden_units_e, state_size)
)

optimiser_e = SGD(emulator.parameters(), lr=0.005)
criterion = nn.MSELoss()

움직임 예시

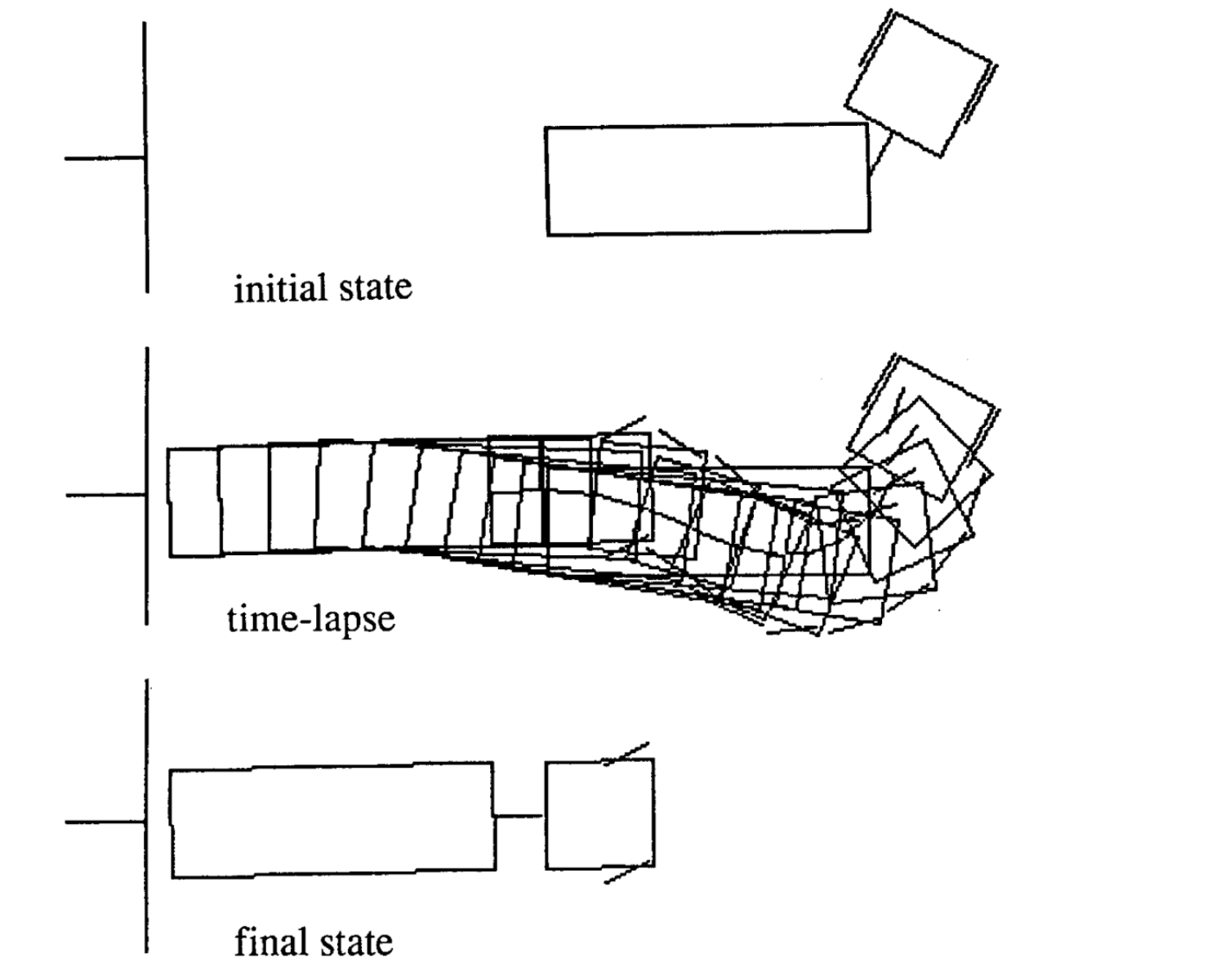
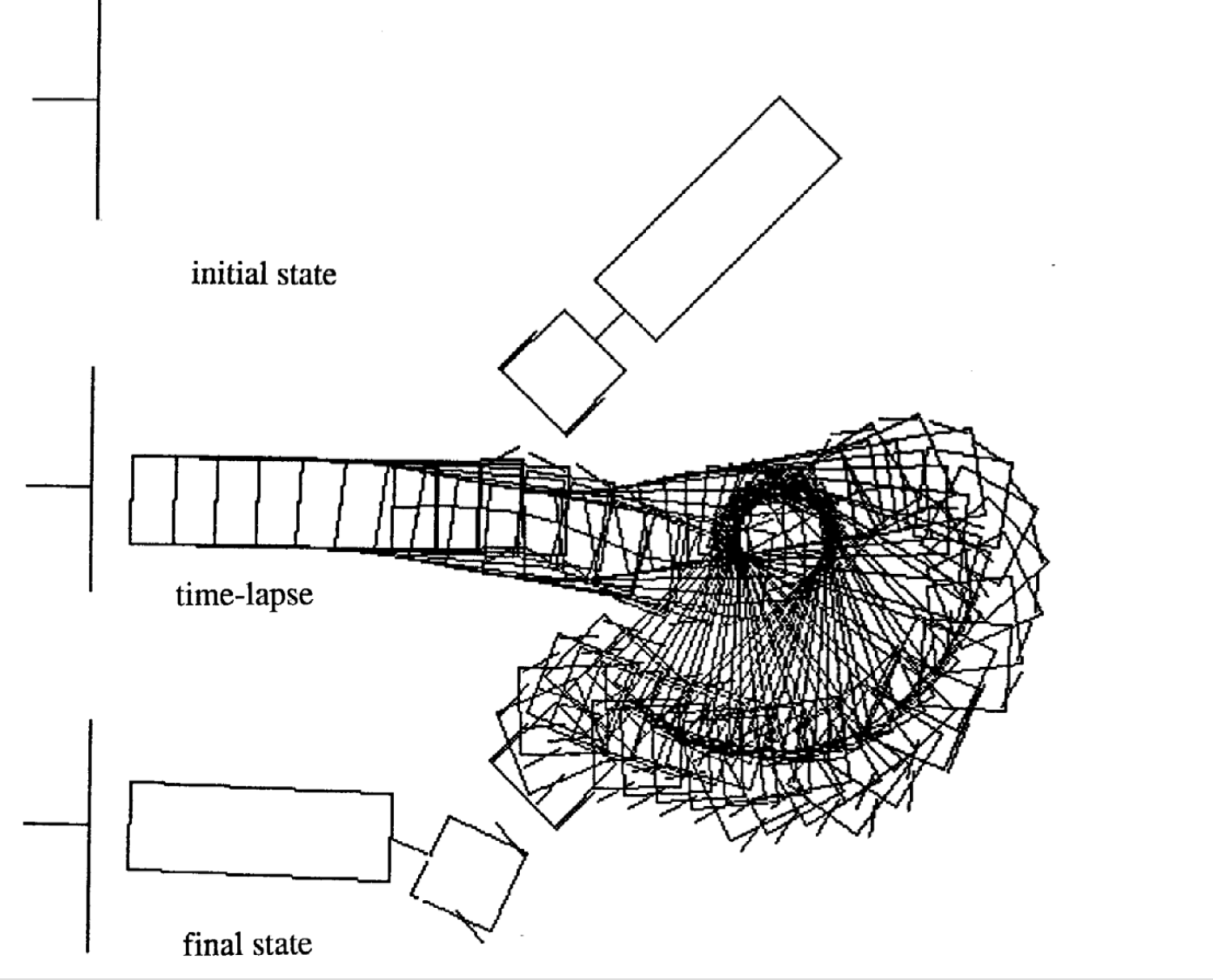
다음은 다른 초기 상태에 대한 네 가지 움직임의 예입니다. 각 에피소드에서 각 시간 스탭의 수가 다른점을 알아야합니다.

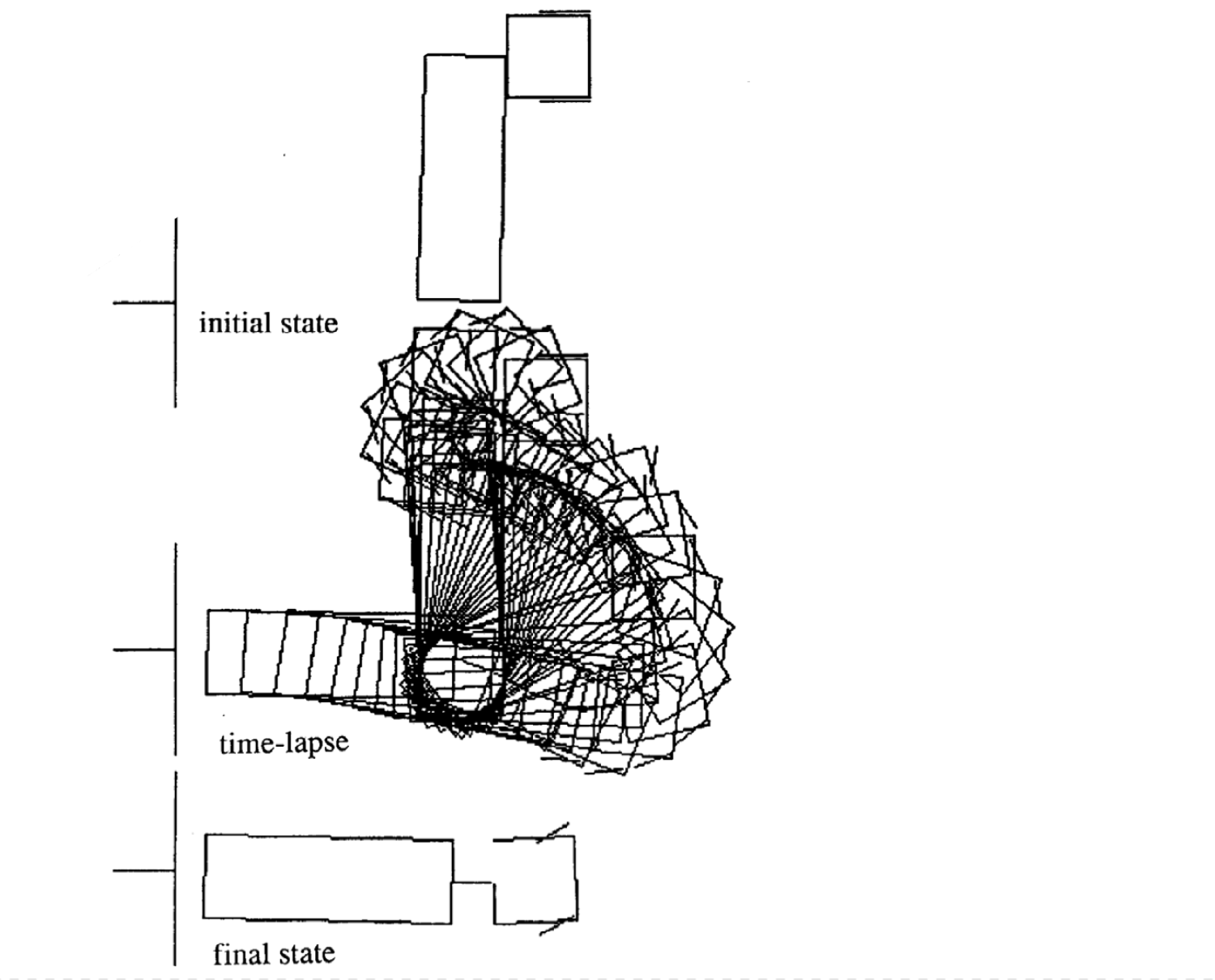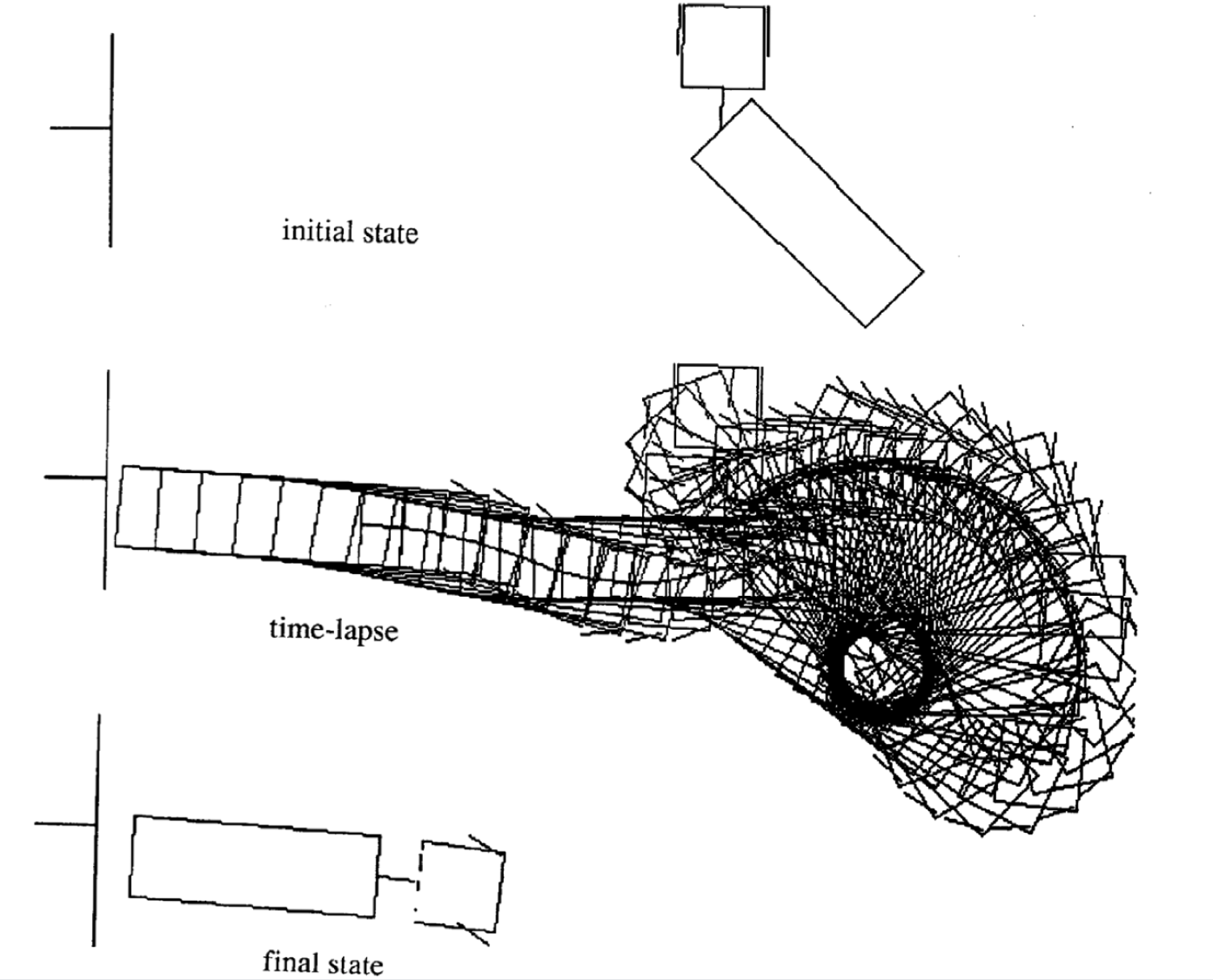추가적인 자료:

전체 작동 데모는 https://tifu.github.io/truck_backer_upper/에서 찾을 수 있습니다. 코드도 https://github.com/Tifu/truck_backer_upper에서 확인할 수 있습니다.