생산적 적대 신경망

생산적 적대 신경망^GANs 소개

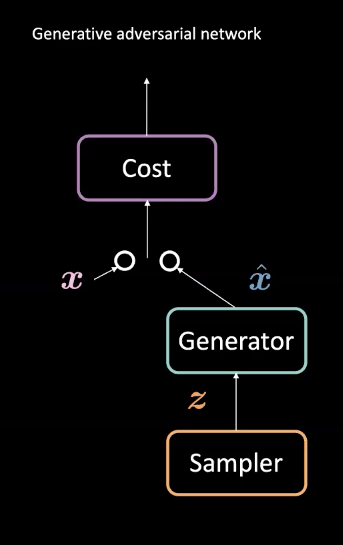
그림 1: 생산적 적대 신경망^GAN 아키텍처

생산적 적대 신경망은 비지도 기계학습에 사용되는 신경망 유형이다. 두 개의 적대적 모듈로 구성되는데: 발생기^generator와 비용^cost 신경망이다. 이 모듈들은 서로 경쟁하는데 발생기가 진짜 예시 $\vect{\hat{x}}$ 생성에 의한 이 필터를 속이려고 노력하는 동안 비용 신경망이 가짜 예시를 걸러내려고 노력하는 것과 같다. 이 경쟁을 통해 모델은 사실적인 데이터를 만들어내는 발생기를 학습한다. 이들은 미래 예측이나 특정 데이터셋에서 훈련된 후 만들어내는 이미지에 대한 것과 같은 과제에 쓰인다.

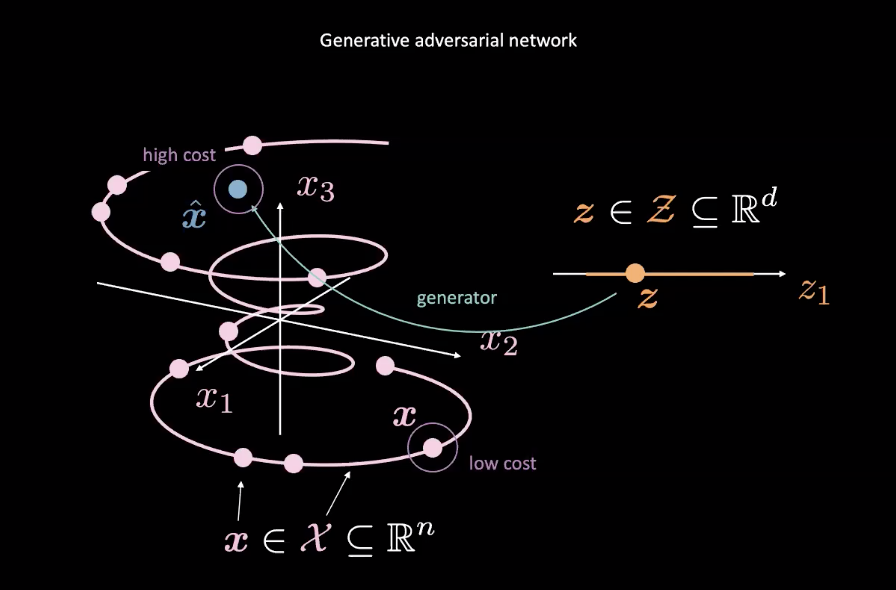
그림 2: 랜덤 변수로부터 맵핑하는 생산적 적대 신경망

생산적 적대 신경망은 에너지 기반 모델의 예시이다. 보통 말하는 비용 신경망은 그림2에서 분홍색 $\vect{x}$에 의해 정의되는 참인 데이터 분포에 근접한 입력값을 위한 낮은 비용을 생산하기 위하여 훈련된다. 그림2의 파란색 $\vect{x}$과 같은 분포로부터 오는 데이터는 높은 비용을 가지고 있을 것이다. 평균제곱오차^{Mean Squared Error} 손실은 전형적으로 비용 신경망의 성능을 계산하기 위하여 쓰인다. 이는 비용 함수가 특정 범위(즉, $\text{cost} : \mathbb{R}^n \rightarrow \mathbb{R}^+ \cup {0}$) 안의 양의 스칼라 값을 출력하는 비용 함수를 기록할 만한 가치가 있다는 것이다. 이것은 그 출력값에 대하여 별개의 분류를 사용하는 고전적인 판별 장치와 다르다.

한편, 비용 신경망을 속이기 위한 실제 생성 데이터에 대한 랜덤 변수 $\vect{z}$의 맵핑을 개선하고자 발생 신경망 ($\text{generator} : \mathcal{Z} \rightarrow \mathbb{R}^n$)을 훈련시킨다. 발생기는 비용 함수의 출력값에 대한 점과 더불어 훈련이 이루어지며 $\vect{\hat{x}}$의 에너지를 최소화하기 위하여 노력한다. 우리는 이 에너지를 $C(\cdot)$가 비용 신경망이고 $G(\cdot)$이 발생 신경망인 곳에 있는 $C(G(\vect{z}))$라 정의한다.

비용 신경망의 학습은 평균제곱오차 손실을 최소화하는 것을 기반으로 하는데, 발생 신경망의 학습은 비용 신경망 최소화를 통하는 동안 $\vect{\hat{x}}$에 관하여 $C(\vect{\hat{x}})$의 경사를 사용한다.

높은 비용이 데이터 매니폴드 바깥 지점에, 낮은 비용이 그 범위 안에 배치되는 것을 보장하기 위하여, 비용 신경망 $\mathcal{L}_{C}$에 대한 손실 함수는 약간의 플러스 이윤 $m$에 대한 $C(x)+[m-C(G(\vect{z}))]^+$이다. $\mathcal{L}_{C}$를 최소화하는 것은 $C(\vect{x}) \rightarrow 0$ and $C(G(\vect{z})) \rightarrow m$를 필요로 한다. 발생기 $\mathcal{L}_{G}$에 대한 손실은 단순히 발생기로 하여금 $C(G(\vect{z})) \rightarrow 0$를 보장하도록 독려하는 $C(G(\vect{z}))$이다. 그러나 이것은 $0 \leftarrow C(G(\vect{z})) \rightarrow m$로서의 불안정성을 일으킨다.

생산적 적대 신경망과 변이형 오토인코더^VAEs 사이의 차이점

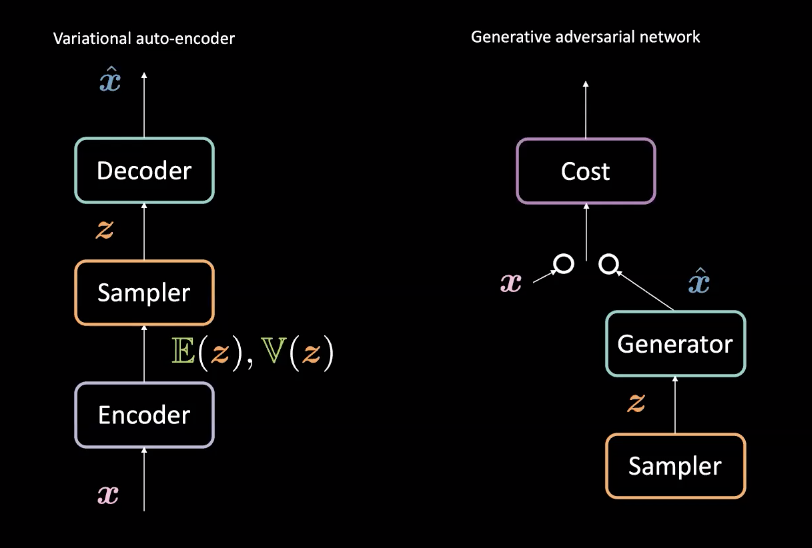
그림. 3: 변이형 오토인코더(왼쪽) vs. 생산적 적대 신경망(오른쪽) - 아키텍처 디자인

8주차에 살펴보았던 변이형 오토인코더와 비교했을 때, 생산적 적대 신경망은 약간 다르게 발생기를 만들어낸다. 다시 살펴보자면, 변이형 오토인코더는 입력값 $\vect{x}$을 인코더^encoder를 동반하는 잠재공간 $\mathcal{Z}$로 연결하고나면 $\mathcal{Z}$ 뒤쪽에서 $\vect{\hat{x}}$를 얻기 위한 디코더^decoder를 동반하는 데이터 공간으로 연결한다. 그러면 $\vect{x}$와 $\vect{\hat{x}}$가 비슷하도록 만드는 재구성 손실을 사용한다. 반면, 생산적 적대 신경망은 위 그림에서 볼 수 있듯이 서로 경쟁하는 발생기와 비용 신경망을 동반한 적대적 세팅을 통해 학습한다. 이러한 신경망은 경사 기반 방법을 통한 역전파를 통하여 성공적으로 학습이 이루어진다. 이러한 아키텍처 차이점은 그림3에서 확인할 수 있다.

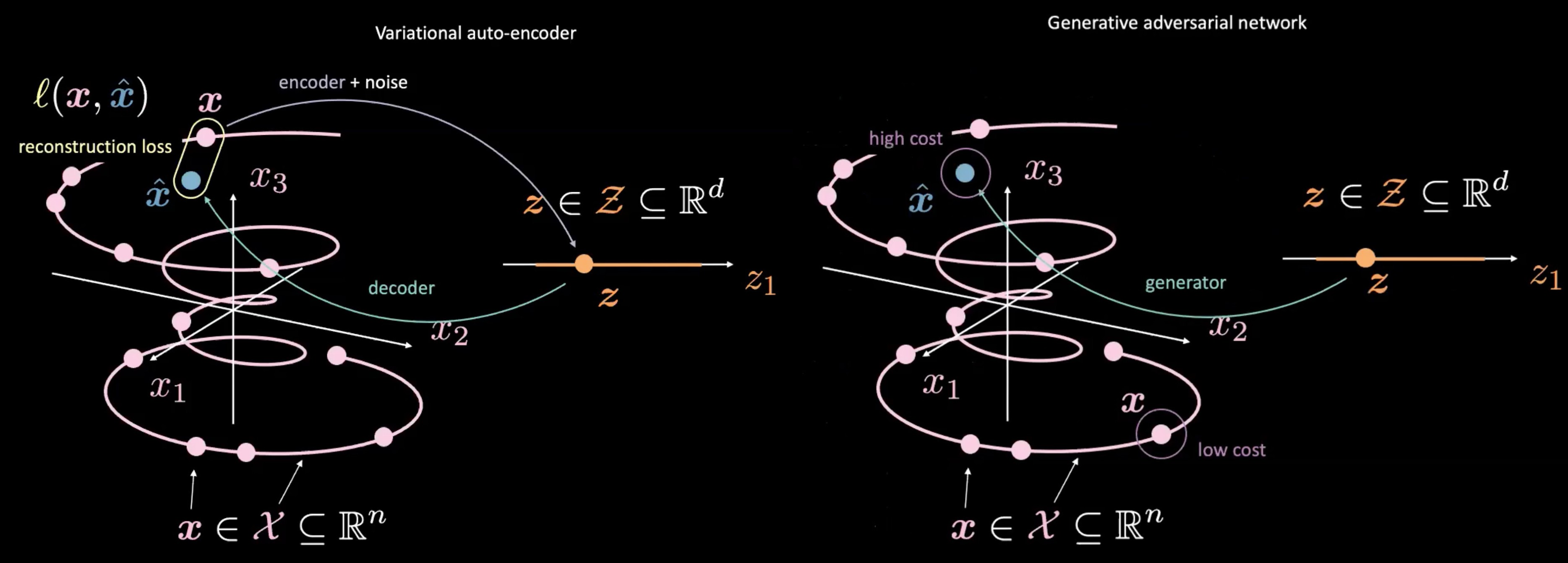
그림. 4: 변이형 오토인코더(왼쪽) vs. 생산적 적대 신경망(오른쪽) - 랜덤 샘플 $\vect{z}$으로부터의 연결

또한 생산적 적대 신경망은 변이형 오토인코더와 다른데 생산적 적대 신경망과 변이형 오토인코더가 $\vect{z}$를 각각 어떻게 만들어내고 사용하는지 여부를 통하여 알 수 있다. 생산적 적대 신경망은 $\vect{z}$를 샘플링하는 것으로 시작하는데, 이 부분은 변이형 오토인코더 안에서의 잠재 공간과 비슷하다. 그러면 $\vect{z}$를 $\vect{\hat{x}}$와 연결하고자 생성 신경망을 이용한다. 이 $\vect{\hat{x}}$는 판별 장치/비용 신경망을 통하여 보내지는데 얼마나 진짜같은지 평가하기 위한 것이다. 변이형 오토인코더와 생산적 적대 신경망의 주요 차이점 중 하나는 ** 우리가 생성 신경망 $\vect{\hat{x}}$의 출력값과 실제 데이터 $\vect{x}$ 사이의 직접적인 관계(즉 재구성 손실)를 판단할 필요가 없다는 것이다.** 대신, 판별 장치/비용 신경망이 실제 데이터 $\vect{x}$ 혹은 더 실제 같은 것들과 비슷한 점수를 만드는 그러한 $\vect{\hat{x}}$를 만들기 위한 발생기를 학습시킴으로써 $\vect{\hat{x}}$가 $\vect{x}$와 비슷해지도록 강제한다.

생산적 적대 신경망에서의 가장 중대한 함정

생산적 적대 신경망이 발생기를 만드는 것에 대하여 강력할 수 있는 반면, 몇 가지 중대한 함정이 있다.

1. 불안정한 수렴

발생기가 학습할수록 개선좋아짐으로써, 판별 장치 성능은 더 나빠지는데 실제와 가짜 데이터 사이의 차이점을 더이상 쉽게 말해줄 수 없기 때문이다. 만약 발생기가 완벽하다면, 실제와 가짜 데이터의 매니폴드는 각각 맨 윗부분에 놓일 것이고 판별 장치는 많은 분류오류를 만들어낼 것이다.

(https://developers.google.com/machine-learning/gan/training)]

이는 생산적 적대 신경망의 수렴에 관한 문제점을 제기한다: 판별 장치 피드백은 시간이 흐를수록 의미가 없어진다. 만약 판별 장치가 완전히 랜덤 피드백을 줄 때 생산적 적대 신경망이 빗나간 학습을 계속한다면, 발생기는 쓸모없는 피드백의 학습을 시작하고 품질은 떨어질 수 있다. [[생산적 적대 신경망에서의 학습 수렴] 참조 –> (https://developers.google.com/machine-learning/gan/training)]

결과적으로 발생기와 판별 장치 사이에는 오히려 균형보다 불안정한 균형점이 있다.

2. 경사 사라짐

생산적 적대 신경망에 대하여 이진 크로스 엔트로피 손실을 사용하는 것을 생각해보자.

판별 장치가 더 확실해짐으로써, $D(\vect{x})$는 $1$에 더 가까워지고 $D(\vect{\hat{x}})$는 $0$에 더 가까워진다. 이 확실성은 비용 신경망의 출력값을 더 평평한 경사가 더 포화상태에 이르는 지점으로 이동시킨다. 이렇게 더 평평한 지역은 잘게 발생 신경망의 학습을 방해하는 경사 사라짐을 준다. 따라서 생산적 적대 신경망을 학습시킬 때, 자신감이 더 생기면 비용이 점차 증가한다는 것을 확실히 해두고 싶어진다.

3. 모드 붕괴

만약 발생기가 모든 $\vect{z}$의 것을 샘플러에서 판별 장치를 바보로 만들 수 있는 단일 $\vect{\hat{x}}$로 연결한다면, 발생기는 오직 그 $\vect{\hat{x}}$를 만들어낼 것이다. 결국, 판별 장치는 분명히 이 가짜 입력값을 탐지하기 위하여 학습할 것이다. 결과적으로, 발생기는 단순히 그 다음으로 가장 맞는 것 같은 $\vect{\hat{x}}$를 찾고 주기를 반복한다. 결과적으로, 판별 장치는 가짜 $\vect{\hat{x}}$의 데이터를 통하여 순환하는 동안 로컬 최소값들 안에 갇히게 된다. 이 이슈에 대한 가능성 있는 해결책은 항상 다른 입력값이 주어지는 같은 출력값을 주는 것에 대한 발생기에 약간의 페널티를 강화하는 것이다.

심층 합성곱 생산적 적대 신경망 (DCGAN) 소스코드

예제 소스코드는 [여기서] https://github.com/pytorch/examples/blob/master/dcgan/main.py 확인할 수 있다.

발생기

1. 발생기는 ‘nn.BatchNorm2d’와 ‘nn.ReLU’로 나누어진 몇개의 ‘nn.ConvTranspose2d’를 언샘플한다.

1. 순차적으로 끝날 때, 신경망은 출력값을 $(-1,1)$로 낮추기 위하여 ‘nn.Tanh()’을 사용한다.

1. 입력값 랜덤 벡터는 $nz$의 사이즈를 갖는다. 출력값은 $nc$가 채널수만큼 있는 곳에서 $nc \times 64 \times 64$의 크기를 갖는다.

class Generator(nn.Module):
    def __init__(self):
        super().__init__()
        self.main = nn.Sequential(
            # 입력값은 합성곱으로 가는 Z이다.			
            nn.ConvTranspose2d(     nz, ngf * 8, 4, 1, 0, bias=False),
            nn.BatchNorm2d(ngf * 8),
            nn.ReLU(True),
            # 상태 크기. (ngf*8) x 4 x 4
            nn.ConvTranspose2d(ngf * 8, ngf * 4, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ngf * 4),
            nn.ReLU(True),
            # 상태 크기. (ngf*4) x 8 x 8
            nn.ConvTranspose2d(ngf * 4, ngf * 2, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ngf * 2),
            nn.ReLU(True),
            # 상태 크기. (ngf*2) x 16 x 16
            nn.ConvTranspose2d(ngf * 2,     ngf, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ngf),
            nn.ReLU(True),
            # 상태 크기. (ngf) x 32 x 32
            nn.ConvTranspose2d(    ngf,      nc, 4, 2, 1, bias=False),
            nn.Tanh()
            # 상태 크기. (nc) x 64 x 64
        )

    def forward(self, input):
        output = self.main(input)
        return output

판별 장치

1. 음의 영역에서 경사를 죽이는 것을 피하기 위한 활성화 함수만큼 ‘nn.LeakyReLU’를 사용하는 것이 중요하다. 이러한 경사없이는 발생기는 업데이트를 받지 않을 것이다.

1. 순차적으로 끝날 때, 판별 장치는 입력값을 분류하기 위하여 ‘nn.Sigmoid()’를 사용한다.

class Discriminator(nn.Module):
    def __init__(self):
        super().__init__()
        self.main = nn.Sequential(
            # 입력값은 (nc) x 64 x 64이다.
            nn.Conv2d(nc, ndf, 4, 2, 1, bias=False),
            nn.LeakyReLU(0.2, inplace=True),
            # 상태 크기. (ndf) x 32 x 32
            nn.Conv2d(ndf, ndf * 2, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ndf * 2),
            nn.LeakyReLU(0.2, inplace=True),
            # 상태 크기. (ndf*2) x 16 x 16
            nn.Conv2d(ndf * 2, ndf * 4, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ndf * 4),
            nn.LeakyReLU(0.2, inplace=True),
            # 상태 크기. (ndf*4) x 8 x 8
            nn.Conv2d(ndf * 4, ndf * 8, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ndf * 8),
            nn.LeakyReLU(0.2, inplace=True),
            # 상태 크기. (ndf*8) x 4 x 4
            nn.Conv2d(ndf * 8, 1, 4, 1, 0, bias=False),
            nn.Sigmoid()
        )

    def forward(self, input):
        output = self.main(input)
        return output.view(-1, 1).squeeze(1)

이 두 클래스들은 ‘netG’와 ‘netD’로서 초기 설정된다.

생산적 적대 신경망을 위한 손실 함수

우리는 목표와 출력값 사이에 이진 교차 엔트로피를 사용한다.

criterion = nn.BCELoss()

구성

우리는 ‘opt.batchSize’ 사이즈와 랜덤 벡터 ‘nz’ 길이의 ‘fixed_noise’를 만든다. 또한 실제 데이터와 ‘real_label’과 ‘fake_label’이라 각각 불리도록 생성된 (가짜) 데이터에 대한 레이블을 만든다.

fixed_noise = torch.randn(opt.batchSize, nz, 1, 1, device=device)
real_label = 1
fake_label = 0

그러면 판별 장치와 발생 신경망을 위한 옵티마이저를 구축하면 된다.

optimizerD = optim.Adam(netD.parameters(), lr=opt.lr, betas=(opt.beta1, 0.999))
optimizerG = optim.Adam(netG.parameters(), lr=opt.lr, betas=(opt.beta1, 0.999))

학습

각 학습 에폭은 두 단계로 나누어진다.

1단계는 판별 장치 신경망을 업데이트하는 것이다. 두 부분에서 이루어지는데 첫 번째는 ‘dataloaders’에서 오는 실제 데이터를 판별 장치에게 공급하고, 출력값과 ‘real_label’ 사이의 손실을 계산한 다음, 역전파와 함께 경사를 축적하는 것이다. 두 번째, ‘fixed_noise’를 사용하는 발생 신경망에 의해 생성된 데이터를 판별 장치에 공급하고, 출력값과 ‘fake_label’ 사이의 손실을 계산한다. 그런 다음 경사를 축적한다. 마지막으로 판별 장치 신경망을 위한 매개 변수를 업데이트하기 위하여 축적된 경사를 사용한다.

판별 장치를 학습시키는 동안 발생기로 전파하는 것으로부터 경사를 멈추기 위하여 가짜 데이터를 떼어낸다는 것을 기억하라.

또한 ‘zero_grad()’를 경사를 없애기 위하여 초기 단계에서 오직 한 번만 불러와야 실제와 가짜 데이터 모두로부터의 경사가 업데이트를 위하여 사용될 수 있다는 것을 기억해야 한다. 두 ‘.backward()’는 이러한 경사 축적을 불러온다. 마지막으로 매개 변수를 업데이트 하기 위한 단 한 번의 ‘optimizerD.step()’ 호출이 필요하다.

# 실제 데이터로 학습시킨다.
netD.zero_grad()
real_cpu = data[0].to(device)
batch_size = real_cpu.size(0)
label = torch.full((batch_size,), real_label, device=device)

output = netD(real_cpu)
errD_real = criterion(output, label)
errD_real.backward()
D_x = output.mean().item()

# 가짜 데이터로 학습시킨다.
noise = torch.randn(batch_size, nz, 1, 1, device=device)
fake = netG(noise)
label.fill_(fake_label)
output = netD(fake.detach())
errD_fake = criterion(output, label)
errD_fake.backward()
D_G_z1 = output.mean().item()
errD = errD_real + errD_fake
optimizerD.step()

2단계는 발생 신경망을 업데이트하는 것이다. 이번에는 판별 장치에 가짜 데이터를 주지만 ‘real_label’로 손실을 계산한다! 이렇게 하는 목적은 사실적인 $\vect{\hat{x}}$’ 데이터를 만들기 위한 발생기를 학습시키기 위한 것이다.

netG.zero_grad()
label.fill_(real_label)  # 가짜 레이블은 발생 비용에 대한 실제이다.
output = netD(fake)
errG = criterion(output, label)
errG.backward()
D_G_z2 = output.mean().item()
optimizerG.step()