세계 모델과 생산적 적대 신경망

자율 제어를 위한 세계 모델

자기지도학습의 가장 중요한 활용 중 하나는 제어를 위한 세계 모델을 배우는 것이다. 인간이 과제를 수행할 때, 세계가 어떻게 돌아가는지에 대한 내부 모델을 갖게 된다. 예를 들어, 우리가 9살 무렵에 대부분 관찰을 통하여 물체 인지 능력을 얻는다. 어떤 의미에서는 자기주도학습과 비슷하다; 미래 예측 학습에서, 우리는 마치 자기주도 모델이 잠재 특징을 학습하는 것과 같은 추상적 원리를 배운다. 하지만 한 단계식 더 나아갈 때, 내부 모델은 그 세계에서 행동하게 한다. 예를 들어, 우리의 물체 인지 능력을 사용할 수 있고 예측을 위하여 우리의 근육이 어떻게 움직이는지, 그리고 떨어지는 펜을 잡을 수도 있다.

“세계 모델”은 무엇인가?

자율 지능 시스템은 크게 네 개의 모듈로 이루어진다(그림 1). 첫째, 지각 모듈은 세계를 관찰하고 상태 표현을 계산한다. 이 표현은 불완전한데 그 이유는 1) 에이전트가 모든 세계를 관찰하지 않고, 2) 관찰 정확도가 제한적이기 때문이다. 또한 feed-forward 모델에서 지각 모듈이 초기 시간 단계에 대하여 유일하게 존재한다는 것에 주목할 가치가 있다. 둘째, 실행 모듈(또는 정책 모듈)은 (표현된) 세계 상태를 기반으로 약간의 동작을 취하는 것을 예상한다. 셋째, 모델 모듈은 (표현된) 세계 상태가 주어진 동작의 결과를 예측하고, 또한 약간의 가능성이 있는 잠재 특징이 주어진다. 이 예측은 다음 상태에 대한 추측으로서의 다음 시간 단계로 이어지고, 초기 시간 단계부터 비롯된 인지 모듈의 역할을 가진다. 그림 2는 이 feed-forward 과정을 상세하게 설명한다. 결국, 비평 모듈은 제안된 행동 수행 비용으로 들어가는 동일하게 예측하는 방향으로 가게 되는데, 예를 들면, ‘펜이 떨어지고 있다고 믿는 속도가 주어진 상태에서, 이 특정 방 근육을 움직인다면 얼마나 심하게 놓칠까?’와 같은 것이다.

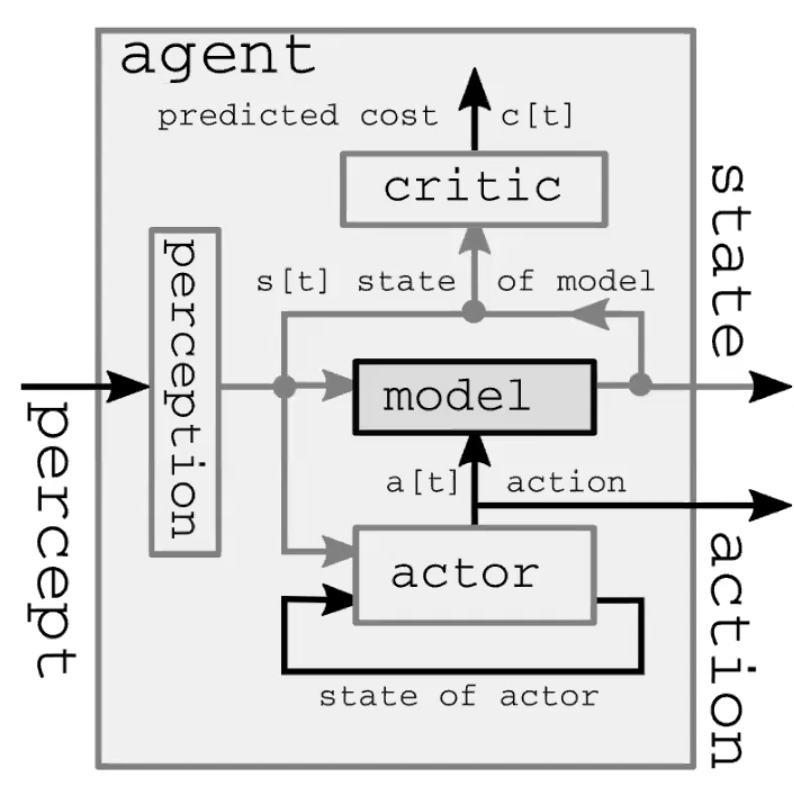
그림. 1: 자율 신경 시스템 설명의 세계 모델 아키텍처

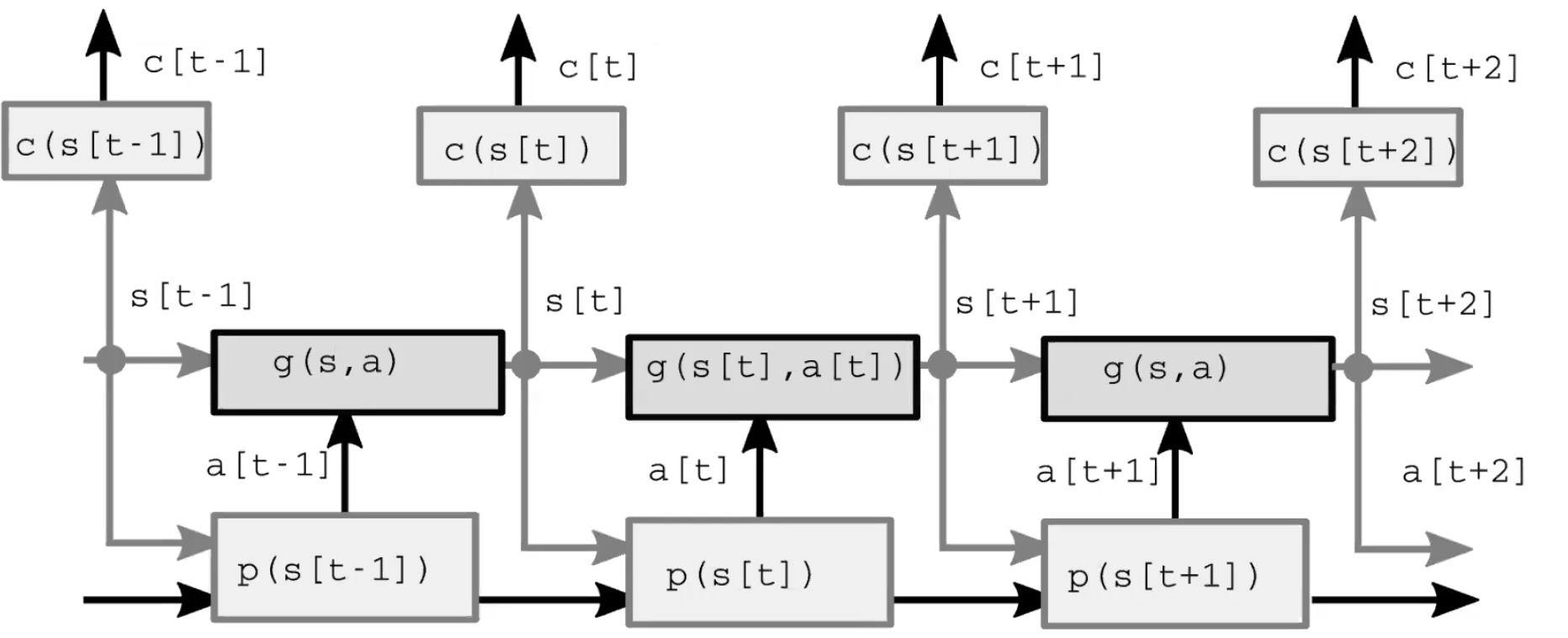
그림. 2: 모델 아키텍처

고전적 설정

고전적인 최적의 제어에서는 배우/정책 모듈이 없고, 오히려 행동 변수가 있을 뿐이다. 이 공식은 1960년대 미항공우주국^NASA이 로켓 궤도를 계산하기 위하여 인간 계산원(대부분 흑인 여성 수학자들)에서 전자식 컴퓨터로 바꾸었을 때 사용했던 모델 예측 제어라 불리는 고전적인 방법에 의해 최적화되어 있다. 우리는 이 시스템을 펼쳐진 순환신경망으로서 그리고 잠재 변수로서 행동들로서 생각할 수 있으며, 역전파와 총 시간 단계 비용을 줄이는 행동의 순서를 추론하기 위한 경사 방법(혹은 분산 행동 집합을 위한 동적 프로그래밍과 같은 다른 방법들도)을 사용할 수 있다.

Aside: We use the word “inference” for latent variables, and “learning” for parameters, though the process of optimizing them is generally similar. One important difference is that a latent variable takes a specific value for each sample, whereas, parameters are shared between samples.

여담: 우리는 잠재 변수에 대하여 “추론”, 매개변수에 대하여 “학습”이라는 단어를 사용하는데, 최적화 과정이 일반적으로 비슷하더라도 사용한다. 한가지 중요한 차이점은 잠재 변수는 각 표본에 대한 특정 값들을 취하는 반면, 매개변수는 표본들 사이에서 공유된다.

개선사항

이제, 우리는 매번 계획을 만들기 원하는 복잡한 역전파 처리과정을 거치는 것을 선호하지 않을 것이다. 이를 추가하기 위하여 우리는 희소 코딩을 개선하기 위한 변형 오토인코더에 대하여 사용했던 같은 속임수를 사용한다.: 우리는 세계 표현에서 비롯한 최적의 행동 순서를 직접적으로 예측하기 위하여 인코더를 훈련시킨다. 이 체제에서 인코더는 정책 신경망이라 불린다.

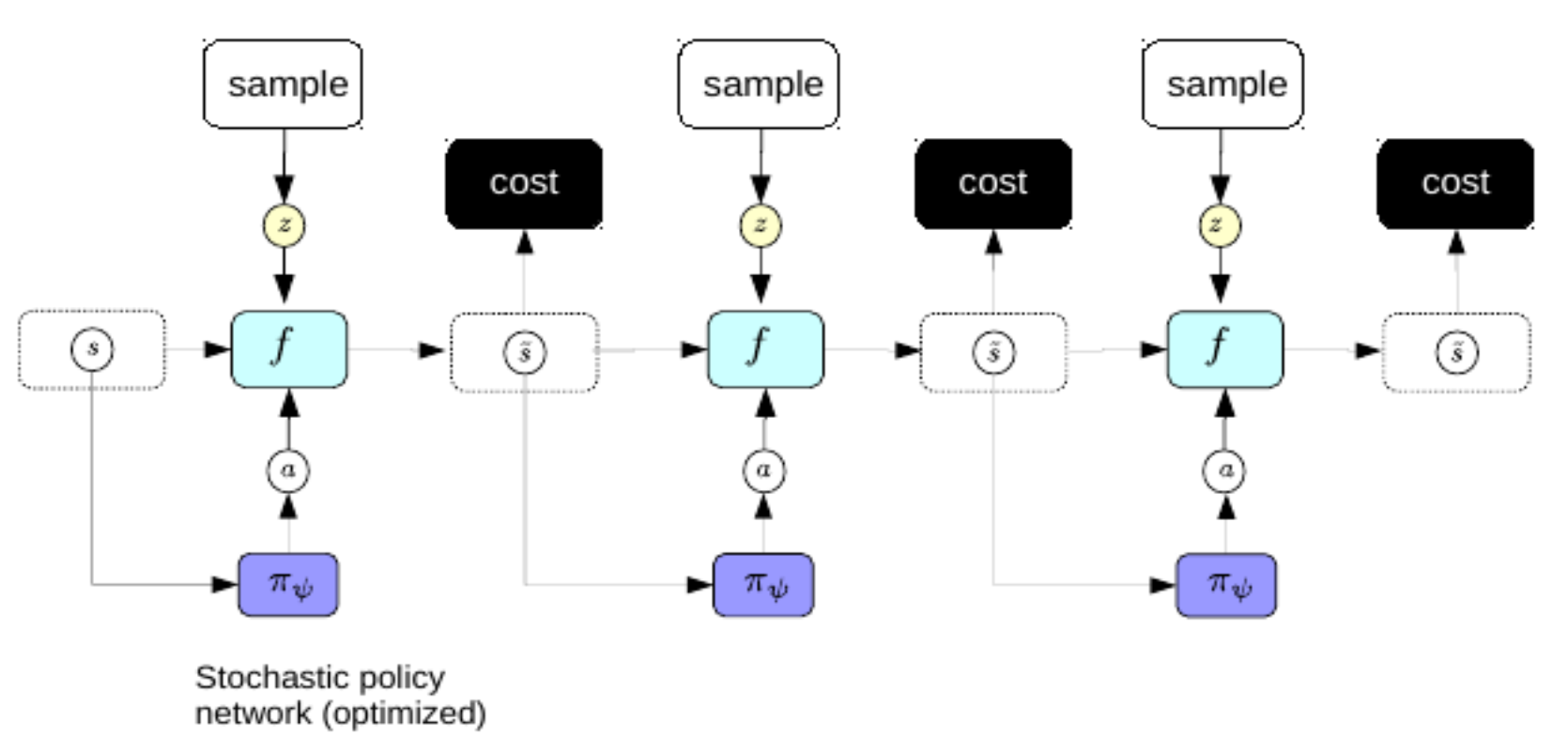
그림. 3: 정책 네트워크.

한번 훈련시켰을 때, 우리는 인지 이후 최적의 행동 순서를 즉시 예측하기 위한 정책 신경망을 사용할 수 있다.

강화학습

강화학습과 우리가 지금까지 공부했던 것의 주요 차이점은 2가지이다.:

1. 강화학습 환경에서는 비용 함수가 블랙박스이다. 즉, 에이전트는 보상 역학을 이해하지 못한다.
2. 강화학습 설정에서, 그 환경으로 가기 위해 세계의 forward 모델을 사용하지 않는다. 대신 우리는 실제 세계와 상호작용하고 무슨 일이 벌어지는지 관찰하는 것으로써 결과를 배운다. 실제 세계에서 세계 상태에 대한 우리의 판단은 완벽하지 않기에 다음에 무슨 일이 벌어질지 예측하는 것은 항상 불가능하다.

강화 학습의 주요 문제점은 비용 함수가 미분 불가능하다는 것이다. 이는 유일한 학습 방법은 시행 착오를 통한 것이다. 그러면 문제는 상태 우주를 효율적인 상태 우주 탐구 방법이 된다. 이것에 대한 해결책을 한번 제시하면 다음 이슈는 ‘탐구 vs 이용’에 대한 근본적인 질문이다.: 환경에 대하여 최대로 학습하기 위하여 행동할 것인지, 아니면 대신에 가능한 높은 보상을 얻기 위하여 학습했던 것을 이용할 것인지?

배우-비평 방법들은 배우와 비평가 모두 학습시키는 강화학습 알고리즘의 인기있는 조합이다. 많은 강화학습 방법들이 비용함수 모델(비평가)을 학습시킴으로써 비슷하게 동작한다. 배우-비평가 방법에서 비평가의 역할은 가치 함수의 기대값을 학습하는 것이다. 이는 모듈을 통한 역전파를 가능하게 하는데, 비평가가 그저 신경망이기 때문이다. 배우의 책임감은 환경을 걷어들이는 행동들을 제안하는 것이고, 비평가의 일은 비용함수 모델을 학습하는 것이다. 배우와 비평가는 비평가가 아무도 없을 때보다 더 효율적인 학습으로 이끄는 2인용 자전거에서 동작한다. 만약 세계의 좋은 모델을 가지고 있지 않다면, 학습하기에 훨씬 어려울 것이다: 예를 들면, 절벽 옆에 있는 차는 절벽에서 떨어지는 것이 나쁜 생각이라는 것을 알지 못할 것이다. 이는 사람과 동물로 하여금 강화학습 에이전트보다 훨씬 빨리 학습하는 것을 가능하게 한다: 우리는 정말로 머리 속에 좋은 세계 모델을 가지고 있는 것이다.

우리는 내재된 불확실성 때문에 세계의 미래를 항상 예측할 수 없다: 우연성의 그리고 인식론적 불확실성. 우연성의 불확실성은 환경 속에서 제어나 관찰할 수 없는 것들 때문이다. 인식론적 불확실성은 미래를 예측할 수 없을 때, 당신의 모델이 충분한 학습 데이터를 가지고 있지 않기 때문이다.

forward 모델은 예측할 수 있기를 원한다

$z$는 우리가 모르는 값의 잠재적 변수이며, $z$가 표현하는 것은 예측에 여전히 영향을 주는 세상에 대해 알 수 없는 것이다.(즉, 우연성의 불확실성). $z$를 희소성, 노이즈, 그리고 인코더를 가지고 규제화할 수 있으며, 계획하기 위한 학습을 목적으로 하는 forward 모델을 사용할 수 있다. 시스템은 상태 표현과 불확실성 $z$의 연결성을 이해하는 디코더를 가짐으로써 동작한다. 가장 좋은 $z$는 $\hat s_{t+1}$와 실제 관측되는 $s_{t+1}$ 사이의 차이를 최소화하는 $z$로 정의되는 것이다.

생산적 적대 신경망

생산적 적대 신경망의 많은 변형 모델이 있는데, 여기서 우리는 대조적인 방법을 사용하는 에너지 기반 모델 형태의 생산적 적대 신경망에 대하여 생각해보고자 한다. 이는 대조 표본 에너지를 밀어올리고 학습 표본 에너지를 밀어내리기도 한다. 기본적인 생산적 적대 신경망은 크게 두 파트로 이루어진다: 똑똑하게 대조 표본을 생산하는 발생기와 본질적으로 비용함수이면서 에너지 모델로서 행동하는 판별 장치(가끔 비평가라 불리기도 함)로 이루어진다. 발생기와 판별기 모두 신경망이다.

생산적 적대 신경망에 대한 두 가지 입력값은 각각 학습 표본과 대조 표본이다. 학습 표본에 대하여, 생산적 적대 신경망은 판별기를 통하여 이러한 표본들을 통과하고 에너지를 줄인다. 대조 표본에 대하여, 생산적 적대 신경망은 약간의 분배로부터 잠재 변수를 표본으로 만들고, 그 변수들을 학습 표본과 유사한 것을 만들기 위한 발생기를 통해 동작하며, 그들의 에너지를 늘리기 위한 판별기를 통하여 그 변수들을 통과시킨다. 판별기에 대한 손실함수는 다음과 같다.:

$L_d$는 $F(y)$를 감소시키고, $F(\bar{y})$를 증가시키는 동안 $F(y) + [m - F(\bar{y})]^+$ 혹은 $\log(1 + \exp[F(y)]) + \log(1 + \exp[-F(\bar{y})])$와 같은 마진 기반 손실함수가 될 수 있다. 이러한 맥락에서, $y$는 레이블이고, $\bar{y}$는 $y$ 스스로를 제외하고 가장 낮은 에너지를 부여하는 응답변수이다. 발생기에 대한 다른 손실함수가 있을 것이다.:

$z$는 잠재 변수에 해당하며, $G$는 발생 신경망이다. 우리는 발생기가 그 가중치를 적응하길 원하고, 판별기를 속일 수 있는 낮은 에너지를 동반한 $\bar{y}$를 만들기를 원한다.

모델의 이 유형이 생산적 적대 신경망이라 불리는 이유는 우리가 서로 양립할 수 없고 그들을 동시에 최소화해야하는 두 가지 객체 함수를 가지고 있기 대문이다. 이는 경사 하강 문제가 아닌데, 왜냐하면 목표가 이 두 가지 함수 사이의 내쉬 균형을 찾기 위한 것이 아니며, 경사하강은 기본값에 의해 이를 통제할 수 없다.

우리가 진실한 매니폴드에 가까운 표본을 가지고 있을 때 문제가 생길 것이다. 우리가 무한히 얇은 매니폴드를 가지고 있다고 가정해보자. 판별기는 매니폴드 바깥에서 $0$인 확률과 매니폴드에서 무한한 확률을 만들어야 한다. 이는 이루기 매우 어려우므로, 생산적 적대 신경망은 시그모이드를 사용하고 매니폴드 밖에서는 $0$을 그리고 매니폴드에서는 $1$을 만든다. 이를 동반한 문제는 만약 우리가 매니폴드 바깥에서 $0$을 만들고자 얻은 판별기에서 시스템을 성공적으로 학습시킨다면, 에너지 함수는 완전히 쓸모없어진다는 것이다. 이는 에너지 함수가 데이터 매니폴드 바깥에 있는 모든 에너지가 무한대가 되고, 데이터에 있는 모든 에너지는 $0$이 되는 곳에서 부드럽지 않기 때문이다. 우리는 매우 사소한 단계에서 에너지값이 $0$에서 무한대로 발산하는 것을 원하지 않는다. 연구자들은 에너지 함수 규제화를 통하여 이 문제를 고치기 위한 많은 방법을 제안하였다. 개선된 생산적 적대 신경망의 좋은 예는 판별기 가중치 사이즈를 제한하는 Wasserstein 생산적 적대 신경망^WGAN이다.