식별하는 순환 희소 오토인코더와 그룹 희소성

식별하는 순환 희소 오토인코더(DrSAE)

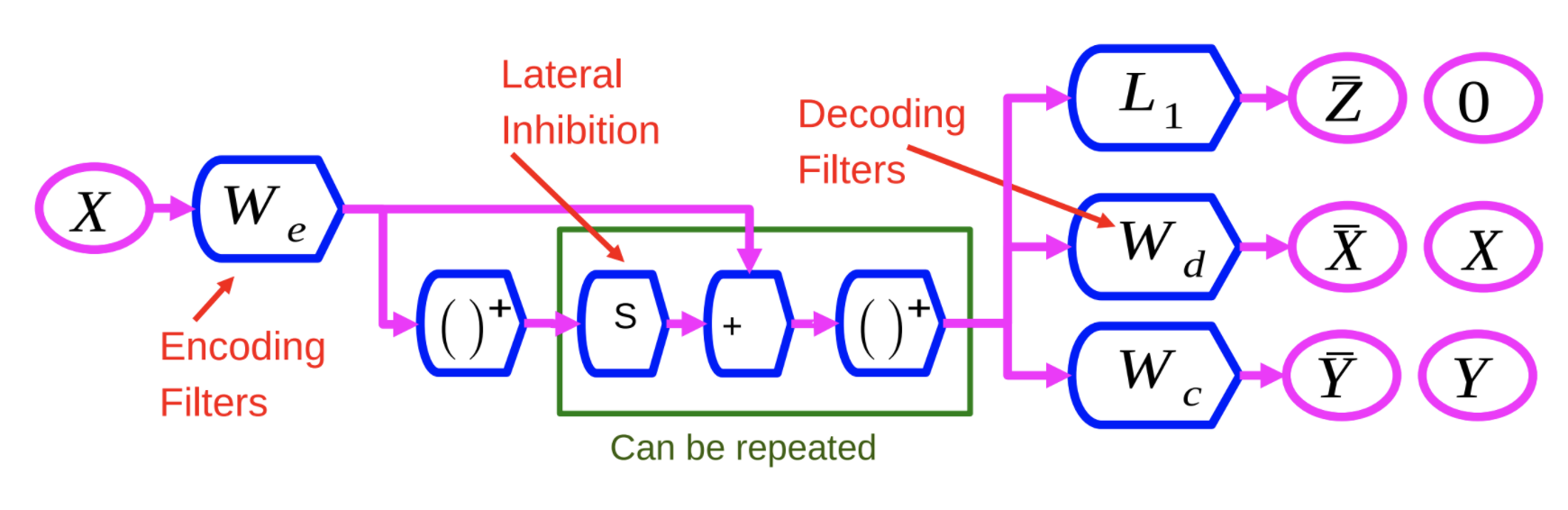
식별하는 순환 희소 오토인코더^DrSAE의 개념은 희소한 코딩 혹은 오토인코더를 식별 학습과 결합하는 것으로 이루어진다.

그림 1: 식별하는 순환 희소 오토인코더 신경망

인코더 $W_e$는 리스타^LISTA에서 쓰는 인코더와 비슷하다. X 변수는 $W_e$를 거쳐 비선형을 통해 실행된다. 그러면 이러한 결과는 다른 학습된 행렬, $W_e$에 추가된 S에 의해 크게 증가하게 된다. 이 과정은 하나의 층위마다 여러번 반복될 수 있다.

우리는 이 신경망을 세 가지의 기준에 따라 학습시킨다:

1. $L_1$: 희소하게 만들기 위하여 특징 벡터 Z를 기준으로 $L_1$을 적용한다.
2. X 재구성: 이것은 출력 단계에서 입력값을 재생산하는 디코딩 행렬을 이용함에 따라 실행된다. 그림1에서 $W_d$가 나타내는 제곱근 오차를 최소화함으로써 이루어진다.
3. 세번째 조건 추가: $W_c$가 나타내는 세번째 조건은 카테고리를 예측하기 위하여 시도하는 단순 선형 분류기이다.

시스템은 이 세가지 기준을 동시에 최소화하기 위하여 학습된다.

이것의 이점은 시스템으로 하여금 입력값을 재구성할 수 있는 표현들을 찾도록 하는 것에 의한 것이며, 여러분은 기본적으로 가능한 입력값에 대한 정보를 많이 담고 있는 특징들을 추출하는 쪽으로 시스템을 편향하고 있다. 즉, 이는 특징들을 강화하는 것이다.

그룹 희소성

여기서의 개념은 희소한 특징들을 생성하기 위한 것이며, 단지 합성곱에 의해 추출되는 보통의 특징들이 아니라 기본적으로 풀링 이후 희소해지는 특징들을 만들어내기 위한 것이다.

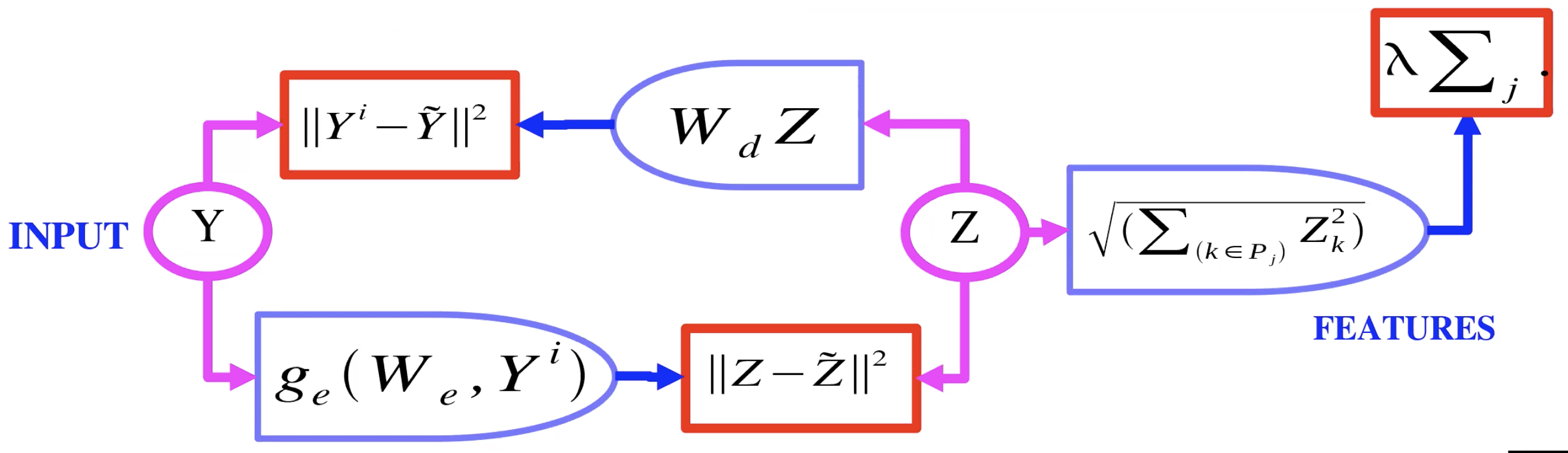
그림 2: 그룹 희소성을 동반한 오토인코더

그림2는 그룹 희소성을 동반한 오토인코더의 예시를 보여준다. 여기서, $L_1$으로 향하는 잠재변수 Z 대신, 기본적으로 $L_2$를 통하여 그룹을 넘어간다. 따라서 여러분은 Z의 한 그룹 안에 있는 각 요소들에 대한 $L_2$ 놈^norm을 얻고, 이러한 놈들의 합을 얻는다. 그래서 이제 그것은 규칙화 도구로서 사용되는 것이며 우리는 이제 Z의 그룹에서 희소성을 가질 수 있다. 이러한 그룹들 혹은 특징들의 풀들은 또 다른 것들과 유사한 특징들을 함께 모으는 경향이 있다.

그룹 희소성을 동반한 오토인코더^AE: 질문과 설명

Q: 첫번째 슬라이드에서 쓰인 분류기와 규제화도구를 동반한 비슷한 전략이 변이형 오토인코더에도 응용될 수 있는지?

A: 변이형 오토인코더에서 노이즈와 희소성을 강제하는 것은 잠재 변수 혹은 코드 정보를 줄이기 위한 두 가지 방법이다. 아이덴티티 함수의 학습을 막으면 된다.

Q: “그룹 희소성을 동반한 오토인코더”슬라이드에서, $P_j$는 무엇인가?

A: p는 특징들의 풀이다. 벡터 z에 대하여 p는 z에서 값들의 부분집합이다.

Q: 특징 풀링에서의 설명

A: (얀이 그룹 희소성을 동반한 오토인코더 표현을 그린다) 인코더는 풀링된 특징들의 $L_2$ 정규화를 사용함으로써 규제화되는 잠재 변수 z를 만들어낸다. 이 z는 이미지 재구성을 위한 디코더에 의해 쓰이게 된다.

Q: 그룹 규제화가 비슷한 특징들을 모으는데 도움이 되는지?

A: 답은 정확히 알 수 없으며, 여기서 이루어진 작업은 계산 파워나 데이터가 순조롭게 쓰일 수 있기 전에 이루어졌다. 아직 기술적 연구가 더 필요한 상황이다.

이미지 단계 학습, 가중치 분할이 아닌 지역 필터

이것이 도움이 되는지 여부에 대한 답은 명확하지 않다. 이것에 관심을 가지는 사람들은 이미지 복구나 어떤 자기지도학습 중 하나에 관심을 가지고 있다. 이는 데이터셋이 매우 작을 때 잘 돌아갈 것이다. 인코더와 복합 셀에 있는 그룹 희소성을 동반하여 학습시키는 디코더를 가지고 있을 때, 사전학습, 디코더를 제거하고 오직 특징 추출기로서 인코더를 사용하는 시스템이 끝난 후, 합성곱 신경망의 첫번째 층위를 말하고 그것의 꼭대기에 있는 두 번째 층위를 붙이면 된다.

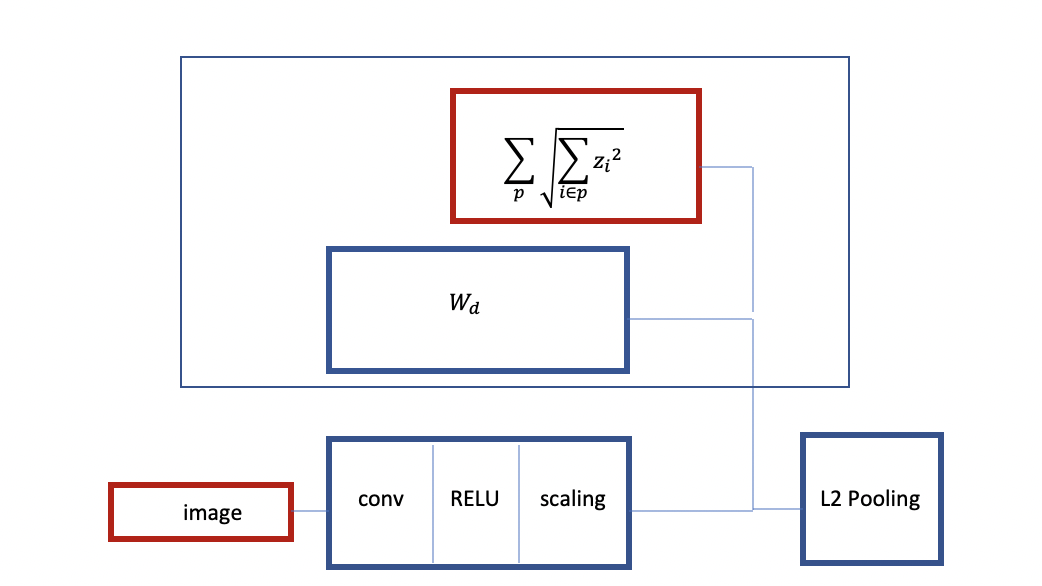
그림 3: 그룹 희소성을 동반한 합성곱 RELU 구조

위에서 볼 수 있듯이, 이미지로 시작되고, 기본적으로 합성곱 RELU와 이 이후의 어떤 스케일링 층위인 인코더를 가진다. 여러분은 그룹 희소성을 동반하여 학습시키게 된다. 선형 디코더와 1에 의한 그룹인 기준을 가지며, 규제화도구로서의 그룹 희소성을 얻게 된다. 마치 그룹 희소성과 비슷한 아키텍처를 동반한 L2풀링과 같다.

또한 이 신경망의 다른 경우를 학습시킬 수도 있다. 이번에는, 층위를 더 추가하고 L2풀링과 희소성 기준을 동반한 디코더를 가질 수 있으며, 꼭대기에 있는 풀링을 동반한 그것의 입력값을 재구성하도록 학습시킬 수 있다. 이것은 사전학습된 2개의 층위로 이루어진 합성곱 신경망을 만들어낼 것이다. 이 방법은 또한 스택 오토인코더라 불리기도 한다. 여기서 주요 특징은 그룹 희소성을 동반한 불변성을 만들어내도록 학습이 이루어진다는 것이다.

Q: 그룹으로서 모든 가능한 하위트리들을 이용해야 하는지?

A: 그것은 여러분의 선택에 달려있다. 원한다면 다수의 트리를 이용할 수 있다. 우리는 필요한 것보다 더 큰 트리를 동반한 트리를 학습시킬 수 있고, 그러고 나면 거의 쓰이지 않은 가지들을 제거할 수 있다.

그림 4: 이미지 단계 트레이닝, 가중치 분할이 아닌 지역 필터

이들은 핀-휠 패턴이라 불린다. 이것은 특징들의 조직 종류이다. 그러한 붉은 점들 주변을 도는 것으로써 계속적이고 다양한 방향성을 나타낸다. 만약 그 붉은 점들 중 하나를 얻고 그 주변을 도는 작은 원을 그린다면, 움직임으로써 계속적으로 생기는 추출기의 방향성을 알게 된다. 이와 비슷한 경향은 뇌에서 관찰된다.

Q: 그룹 희소성이라는 것은 작은 값을 갖기 위해 학습되는지?

그룹 희소성은 규제화도구이다. 그 자체가 학습되는 것은 아니며, 고정되어 있다. 단지 그룹들의 L2 정규화이며 그 그룹들은 사전에 결정된다. 하지만 하나의 기준이기 때문에 인코더와 디코더가 무엇을 할지 어느 정도의 특징들이 추출될지 결정한다.

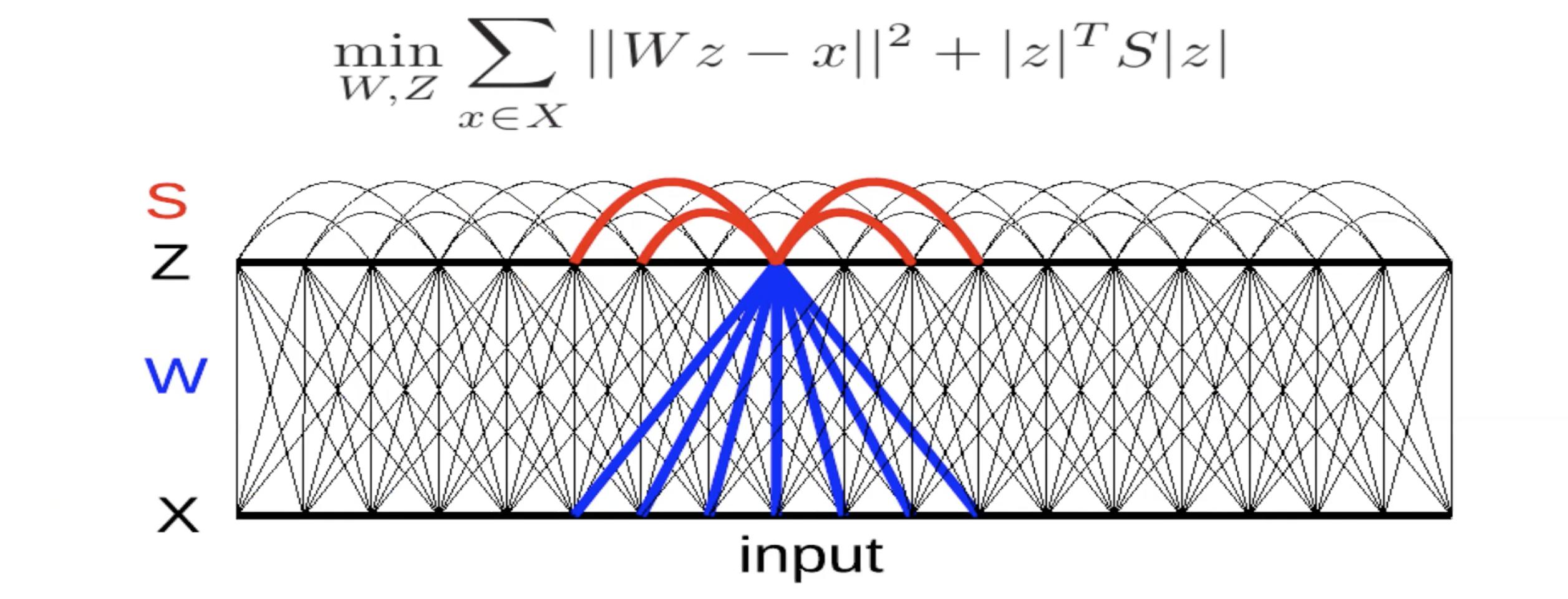
그림 5: 측면억제를 통한 불변의 특징들

광장 복원 오류를 동반한 선형 디코더가 있다. 에너지 안에서의 기준이 있다. 행렬 S는 손에 의해 결정되거나 이 항을 최대화하기 위해 학습된다. 만약 S 안에 있는 항들이 양이면서 크다면, 시스템이 $z_j$를 원하지 않고 $z_j$가 동시에 있기를 원한다는 것을 암시한다. 따라서, 일종의 상호 억제인 셈이다. (뇌과학에서는 자연 억제라 불린다.) 그러므로 최대한 큰 S에 대한 값을 찾도록 노력하게 된다.

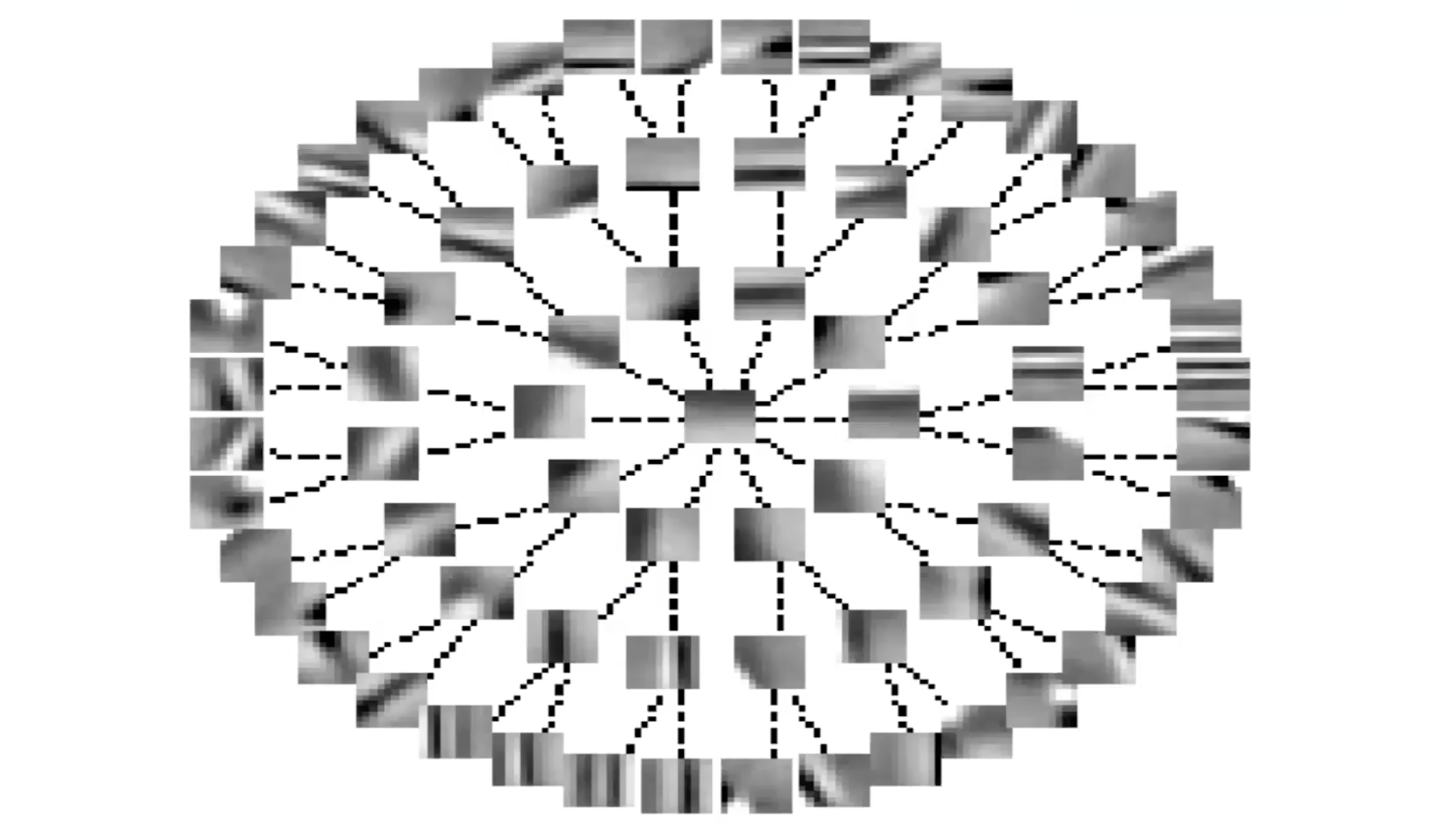
그림 6: 측면 억제를 통한 불변의 특징들(트리 형태)

만약 트리 측면에서 S를 조직한다면, 선들은 S 행렬 안의 0인 항들을 표현한다. 선이 없을 때마다, 0이 아닌 항이 생긴다. 그래서 모든 특징은 그것으로부터 위 혹은 아래에 있는 것들을 제외한 모든 다른 특징들을 억제한다. 이것은 마치 그룹 희소성의 정반대같은 것이다.

시스템이 더 많거나 적은 계속적인 방식으로 특징들을 조직하는 것을 다시 보게 된다. 트리의 가지를 따라 놓여 있는 특징들은 선택성의 다른 단계를 동반한 같은 특징을 표현한다. 주변을 따라 놓여있는 특징들은 계속적으로 더 많이 혹은 더 적게 달라지는데 억제가 없기 때문이다.

각 반복 단계에서 이 시스템을 학습시키려면 $x$를 부여하고 이 에너지 함수를 최소로 만드는 $z$를 찾으면 된다. 그런 다음, $W$를 업데이트 하기 위한 경사 하강법 한 단계를 시행하면 된다. 또한 $S$의 항들을 더 크게 만들기 위한 경사 상승법을 시행할 수도 있다.